Limiti teoremi reti elettriche (1/2)

3. Elementi parassiti nelle connessioni
33
S. SaponaraSaponara- Costruzioni Elettroniche
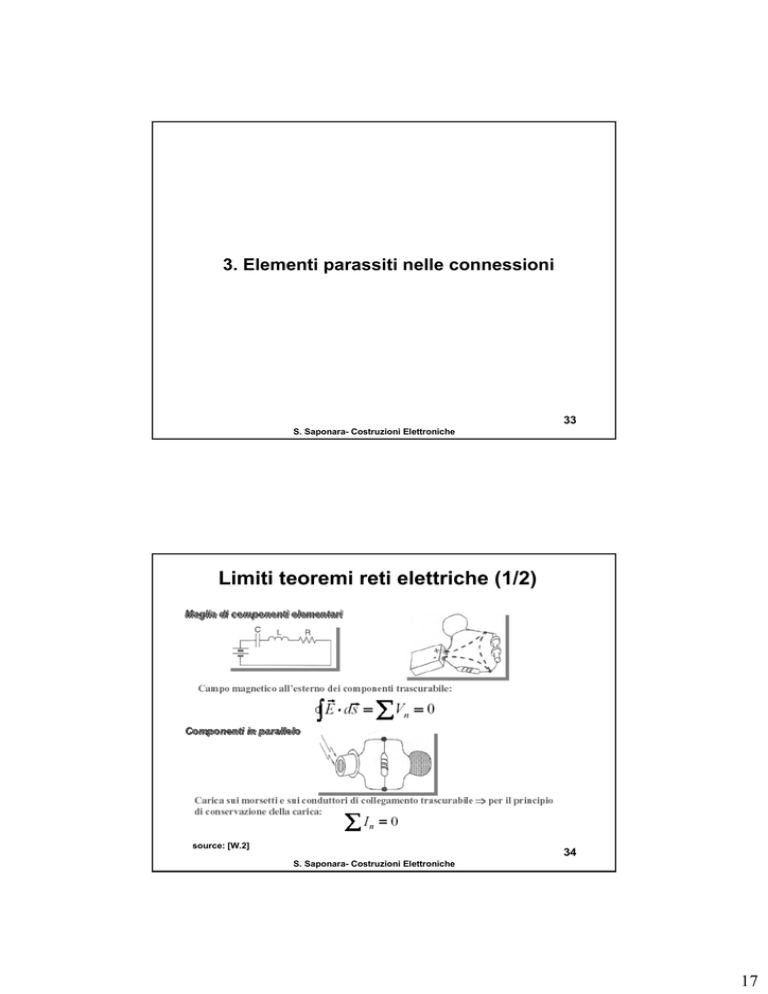
Limiti teoremi reti elettriche (1/2)
source:
source: [W.2
[W.2]]
34
S. SaponaraSaponara- Costruzioni Elettroniche
17
Limiti teoremi reti elettriche (2/2)
source:
source: [W.2
[W.2]]
35
S. SaponaraSaponara- Costruzioni Elettroniche
Elementi parassiti nelle connessioni
source:
source: [W.2
[W.2]]
36
S. SaponaraSaponara- Costruzioni Elettroniche
18
Resistenza parassita del collegamento
source:
source: [W.2
[W.2]]
37
S. SaponaraSaponara- Costruzioni Elettroniche
Unità di misure
Oltre a AWG spesso si trovano mils ed inchs invece che mm e cm
E.g. 6 mils = 6 x 10-3 inches = 15.24 x 10-3 cm = 0.1524 mm
Tabella di
Conversione
Pollici
inchs
Pollici
inchs
Centimetri
cm
Millesimi di
pollice
mils
Millimetri
mm
cm / 2.54
mils / 1000
mm / 25.4
(mils / 1000) *
2.54
mm / 10
Centimetri
cm
inchs *
2.54
Millesimi di
pollice
mils
inchs /
1000
(cm / 2.54) /
1000
Millimetri
mm
inchs *
25.4
cm * 10
(mm / 25.4) /
1000
(mils / 1000) *
25.4
38
S. SaponaraSaponara- Costruzioni Elettroniche
19
Autoinduttanza parassita dei collegamenti (1/3)
Autoinduttanza - Conduttore su piano di massa
Come si ricava la formula? (vedi slide 40 e 41)
source:
source: [W.2
[W.2]]
39
S. SaponaraSaponara- Costruzioni Elettroniche
Autoinduttanza parassita dei collegamenti (2/3)
source:
source: [W.1
[W.1]]
40
S. SaponaraSaponara- Costruzioni Elettroniche
20
Autoinduttanza parassita dei collegamenti (3/3)
Teorema immagini applicato a conduttore su piano di massa (idealmente
(idealmente infinito)
Slide 39 vs. 41
porre s/r
s/rw = 4h/ Φ
essendo
s=2h e rw=Φ/2
source:
source: [W.1
[W.1]]
41
S. SaponaraSaponara- Costruzioni Elettroniche
Mutua induttanza parassita dei collegamenti (1/2)
source:
source: [W.2
[W.2]]
Valore della mutua induttanza LM nel caso di coppia di conduttori su piano
di massa
42
S. SaponaraSaponara- Costruzioni Elettroniche
21
Mutua induttanza parassita dei collegamenti (2/2)
Formula di mutua induttanza si ricava da teorema immagini applicato
applicato a coppia
conduttori su piano di massa (idealmente infinito)
43
source:
source: [W.1
[W.1]]
S. SaponaraSaponara- Costruzioni Elettroniche
Capacità parassita dei collegamenti (1/2)
source:
source: [W.2
[W.2]]
44
S. SaponaraSaponara- Costruzioni Elettroniche
22
Capacità parassita dei collegamenti (2/2)
Teorema immagini applicato a conduttore su piano di massa (idealmente
(idealmente infinito)
Slide 44 vs. 45, porre s/r
s/rw = 4h/Φ
4h/Φ essendo s=2h e rw=Φ/2
source:
source: [W.1
[W.1]]
45
S. SaponaraSaponara- Costruzioni Elettroniche
Capacità mutua parassita dei collegamenti
46
S. SaponaraSaponara- Costruzioni Elettroniche
23
4. Effetti dei parassiti sui segnali (signal integrity)
47
S. SaponaraSaponara- Costruzioni Elettroniche
“There are two kinds of design engineers:
engineers:
those that have signal integrity problems,
and those that will”
E. Bogatin, CEO - GitaTest lab, Agilent Inc
48
S. SaponaraSaponara- Costruzioni Elettroniche
24
Ringing
source:
source: [W.2
[W.2]]
49
S. SaponaraSaponara- Costruzioni Elettroniche
Effetto ringing sul segnale di clock
source:
source: [W.2
[W.2]]
50
S. SaponaraSaponara- Costruzioni Elettroniche
25
Effetto del ringing: esempio (1/3)
Driver TTL (Rout
(Rout di 30 Ω e trise 2 ns)
ns) pilota carico capacitivo di 15 pF
tramite filo in rame AWG30 di 10 cm a 5mm da piano di massa
da formule precedenti calcolo i parassiti (R=25 m Ω, L=85 nH,
nH, C=1.3
C=1.3 pF)
pF)
e simulo in Spice circuito equivalente
R1
R3
V1 = 0
V2 = 3.7
TD = 0
TR = 2n
V2
30
C2
15p
V1 = 0
V2 = 3.7
TD = 0
TR = 2n
V130
R2
L1
25m
85nH
C1
16.3p
0
0
Reale
Ideale
51
S. SaponaraSaponara- Costruzioni Elettroniche
Effetto del ringing: esempio (2/3)
trise = 2 ns
Reale ringing a 5ns con
picco fino a 5.4 V
Ideale No ringing
52
S. SaponaraSaponara- Costruzioni Elettroniche
26
Effetto del ringing: esempio (3/3)
ma con trise = 20 ns ringing sparisce
Reale ringing
trascurabile
Ideale No ringing
53
S. SaponaraSaponara- Costruzioni Elettroniche
Innesco del ringing
•
Dipende se il segnale innesca risonanza di gruppo RLC di
circuito con parassiti
Risposta in frequenza di
circuito con parassiti ha
picco di risonanza a 130 MHZ
Problema è con segnali (digitali o analogici) con fronti di variazione veloci
veloci
54
S. SaponaraSaponara- Costruzioni Elettroniche
27
Crosstalk da capacità mutua (1/2)
source:
source: [W.2
[W.2]]
55
S. SaponaraSaponara- Costruzioni Elettroniche
Simulo in Spice
R1
V4
4.5Vdc
30
C1
15p
0
C3
2p
R2
V1 = 0.8
V2 = 4.5
V5
30
C2
15p
TR = 2n
0
56
S. SaponaraSaponara- Costruzioni Elettroniche
28
Crosstalk da capacità mutua (2/2)
CrosstalkCrosstalk- disturbo su
seconda linea di circa
100 mV
57
S. SaponaraSaponara- Costruzioni Elettroniche
Crosstalk da induttanza mutua
source:
source: [L.2
[L.2]]
58
S. SaponaraSaponara- Costruzioni Elettroniche
29
Crosstalk da impedenza comune a massa
Variazione di corrente a massa di circuito 2 causa, tramite l’
l’impedenza
comune di massa, una variazione della tensione di riferimento del
del circuito
1 e viceversa
source:
source: [L.2
[L.2]]
59
S. SaponaraSaponara- Costruzioni Elettroniche
Correnti di ritorno a massa (1/2)
Le correnti di richiusura seguono sempre le linee a minima impedenza
Cammino a resistenza minima
source:
source: [L.1
[L.1]]
A bassa frequenza (segnali lenti) le correnti si richiudono secondo
secondo il
cammino a resistenza minima (si disperdono per il piano di massa)
massa)
60
S. SaponaraSaponara- Costruzioni Elettroniche
30
Correnti di ritorno a massa (2/2)
Ad alta frequenza (segnali digitali veloci o analogici RF) le correnti
correnti si
richiudono secondo il cammino a induttanza minima
Cammino a induttanza minima
source:
source: [L.1
[L.1]]
La corrente di ritorno giace sotto il conduttore minimizzando l’area
l’area del
loop del circuito e quindi la relativa induttanza
61
S. SaponaraSaponara- Costruzioni Elettroniche
Crosstalk da impedenza comune di
alimentazione
source:
source: [L.2
[L.2]]
Variazione di corrente assorbita da circuito 2 (I2) causa, tramite le
impedenze comune delle linee di alimentazione, una variazione della
della
tensione di alimentazione del circuito 1 e viceversa
62
S. SaponaraSaponara- Costruzioni Elettroniche
31
Esempio di fonti di crosstalk in sistema
reale: ricevitore RF
source:
source: [L.2
[L.2]]
63
S. SaponaraSaponara- Costruzioni Elettroniche
Contenuto frequenziale segnali- fronte (1/2)
source:
source: [W.1
[W.1]]
64
S. SaponaraSaponara- Costruzioni Elettroniche
32
Contenuto frequenziale segnali- fronte (2/2)
source:
source: [W.1
[W.1]]
65
S. SaponaraSaponara- Costruzioni Elettroniche
Contenuto frequenziale segnali- clock (1/2)
source:
source: [W.1
[W.1]]
66
S. SaponaraSaponara- Costruzioni Elettroniche
33
Contenuto frequenziale segnali- clock (2/2)
Empiricamente in letteratura si pone come limite di
banda 1/2·
1/2·trise o 1/π
1/π·trise
source:
source: [W.1
[W.1]]
67
S. SaponaraSaponara- Costruzioni Elettroniche
Contenuto frequenziale segnali e ringing
Limite di banda 1/2·
1/2·trise o 1/π
1/π·trise significa:
160 ÷ 250 MHz per segnale trise a 2 ns che infatti
innescava risonanza a 130 MHz (slide 52)
16 ÷ 25 MHz per segnale a trise 20 ns che non lo
innescava (slide 53)
68
S. SaponaraSaponara- Costruzioni Elettroniche
34