Corrente elettrica
Q
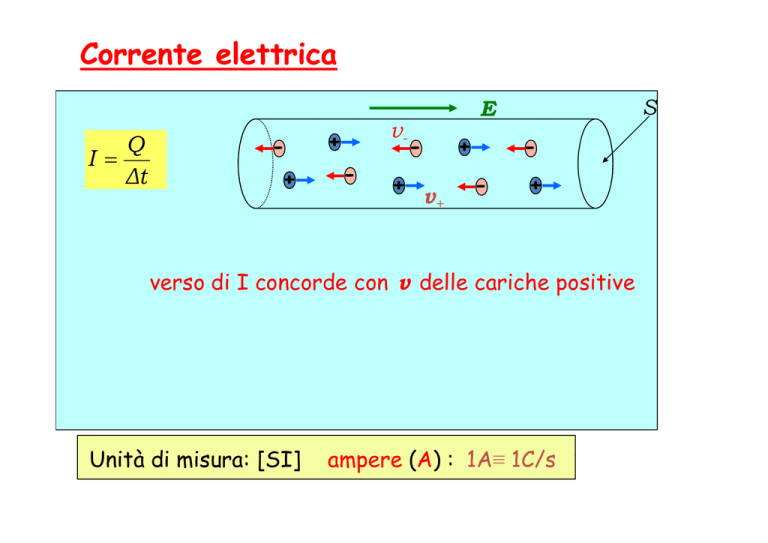
I =
Δt
+
v-
+
-
+
S
E
-
+
v+
-
+
verso di I concorde con v delle cariche positive
Unità di misura:
misu : [SI]
ampere
mp
(A) : 1A≡
1A 1C/s
Campo B di un filo rettilineo percorso
da corrente
I
B
μ I
B=
2π r
Legge di Biot e Savart
La permeabilità magnetica
Generalmente si usa : μ
= μr μ0
permeabilità
bili à magnetica
i
relativa al vuoto del mezzo
considerato
μ 0 = 4π × 10 −7 = 12,56 × 10 −7 kgmC -2
permeabilità magnetica nel vuoto
sostanze
diamagnetiche
μr<1
rame
argento
acqua
sostanze
paramagnetiche
μr>1
aria
alluminio
platino
sostanze
ferromagnetiche
f
g
μr>>1 ferro
nichel
cobalto
Le linee di forza del campo
p B sono
sempre delle curve chiuse che
racchiudono al loro interno qualche
corrente
t elettrica
l tt i
Il campo magnetico di più correnti
Il campo
m m
magnetico
ti prodotto
d tt iin un punto
t d
dello
ll sspazio
i d
da
più correnti è uguale al vettore risultante dei campi
magnetici che ciascuna corrente genererebbe se essa
soltanto fosse presente.
Campo magnetico di due fili
z
i2
i1
i2
i1
y
B1
B2
x
B1B2
Il vettore Forza magnetica
(il prodotto
d tt vettore)
vettore
tt
)
Fm
B
Verso:
θ
v
direzione :
Fm ┴v e
Fm = qvΛΒ
Fm = qvB sin θ
┴
B
modulo: F m = q vBsin θ≡ q p
per area
del parallelogramma di lati v e B
Fm ┴v (Il) e
┴
B
Fm = IlΛΒ
Fm = IlB sin θ
Corrente elettrica
+
Q
I =
Δt
v-
+
-
+
S
E
-
+
v+
-
+
verso di I concorde con v delle cariche positive
Q = IΔt ⇒
Qv = IΔt × v = IΔt × l/Δt = Il
equivalenza carica
carica-in-moto
in moto elemento
elemento-di-corrente
di corrente
Unità di misura:
misu : [SI]
ampere
mp
(A) : 1A≡
1A 1C/s
Forza magnetica
I° caso: carica q in moto in presenza di
un filo percorso dalla corrente I.
I
I
I
r
┴ allo
schermo
h
-
v
Fm
v
Fm
I
Fm
v
v
+
v
r
+F
m
v
Fm
-
v +
Fm=0
+
Fm
r
Iqv
e dipende dall’orientazione di v rispetto al filo
Fm ∝
r
r
Forza magnetica Forza tra cariche in moto
II° caso: Forza tra fili paralleli percorsi da corrente.
F12 F21
I2
I1
r
I1I 2
Fm ∝
r
F12
F21
I1
I2
r
e dipende dall’orientazione reciproca dei fili
Forza magnetica
q
III° caso: carica q in moto in presenza
di magneti
g
permanenti.
p
S
S
+ v
q
N
v
N
Fm ┴ v
Fm ∝ qv
Il vettore Forza magnetica
(il prodotto
d tt vettore)
vettore
tt
)
Fm
B
Verso:
θ
v
direzione :
Fm ┴v e
Fm = qvΛΒ
Fm = qvB sin θ
┴
B
modulo: F m = q vBsin θ≡ q p
per area
del parallelogramma di lati v e B
Fm ┴v (Il) e
┴
B
Fm = IlΛΒ
Fm = IlB sin θ
Il campo di induzione magnetica
Campo di Induzione Magnetica:
(Fm )max
(Fm )max
B =
⇔ B =
qv
IΔl
Direzione di un ago magnetico con verso dal polo sud
al polo nord
Unità di misura: [SI]
tesla (T)
1 gauss=10-4 tesla
1T ≡ 1N.s/(C.m)
L’induzione magnetica
Fm
I
B
Fm
normale
B
B
θ=90°
90
θ=45°
45
θ=0°
Risonanza Magnetica Nucleare (RMN)
Esposizione del paziente a campo magnetico
B
B nμI
B=nμI
B
RMNucleare
Se sottoposti ad un campo magnetico
esterno gli spin dei protoni si ALLINEANO
B0
S
N
Il vettore Forza magnetica
(il prodotto
d tt vettore)
vettore
tt
)
Fm
B
Verso:
θ
v
direzione :
Fm ┴v e
Fm = qvΛΒ
Fm = qvB sin θ
┴
B
modulo: F m =qvBsinθ≡
q
q p
per
area del parallelogramma di lati
v e B
Fm ┴v (Il) e
┴
B
Fm = IlΛΒ
Fm = IlB sin θ
Forza
F z agente
g
su
u una
u
carica in moto.
m
.
Fm = ma
Se v
┴
B
v2
qvB = m
R
mv
R=
qB
q
Traccia di un elettrone in
una camera a bolle. La
curvatura è dovuta a un
campo B perpendicolare
allo schermo.
La spiralizzazione è dovuta
a perdita di velocità per la
presenza dell’idrogeno
Un protone percorre in senso orario un’orbita
circolare di raggio R
R= 2.5
.5 cm con velocità vv=2x10
x 06
m/s in un piano orizzontale posto in una regione dello
spazio dove è presente un campo di induzione
magnetica. Indicare
d
d
direzione e verso del
d l campo di
d
induzione B e calcolarne l’intensità (mp=1.67x10-27kg)
Una sorgente posta in S emette, con velocità iniziale trascurabile, due tipi di particelle
cariche aventi la stessa carica q e masse m1 e m2=2m1. Nel tratto SF le particelle
vengono accelerate da una differenza di potenziale V. Nel tratto FA non sono soggette
a forze;
f
iin A entrano
t
iin una zona di campo magnetico
ti uniforme
if
B ortogonale
t
l all piano
i
della figura e vanno a colpire il rivelatore nei punti C e D. Si chiede:
1) quanto vale il rapporto v1/v2 nel punto A
2) quanto
t vale
l il rapporto
t AD/AC
3) Quali particelle arrivano in C
S
F
A
Il dispositivo è nel vuoto. Trascurare la forza di gravità
1
1
mv 2
2
2 qV
; v2 =
v1 =
m1
qV =
v1
=
v2
2
2
v2
B = m
qvB
R
2R2
AD
=
=
AC
2R1
2 qV
m2
R1 =
m1v1
mv
2m v
; R2 = 2 2 = 1 1 = 2 R1
qB
qB
qB 2
2
3 Le particelle di massa m1.
C
D












