corso di laurea in matematica

CORSO DI LAUREA IN MATEMATICA
PRESENTAZIONE
La Matematica è disciplina di base e di supporto per tutta la ricerca scientifica e tecnologica.
Anche se storicamente i suoi legami più profondi sono quelli con la Fisica, nell’ultimo secolo la Matematica è diventata
strumento essenziale per l’informatica, la biologia, l’economia,..., discipline dalle quali la ricerca matematica trae
stimoli e problemi, al punto che diventa sempre meno definita la tradizionale distinzione tra Matematica Pura e
Matematica Applicata.
Ai filoni tradizionali dell’Algebra, dell’Analisi Matematica, della Fisica Matematica, della Geometria e della Logica
Matematica si è affiancato quello della Matematica Computazionale e almeno le nozioni basilari di questi settori della
Matematica debbono ormai far parte della cultura scientifica di base non solo di chi voglia dedicarsi alla ricerca, ma
anche di coloro che sono impegnati professionalmente nel campo delle applicazioni economiche, tecnologiche e
industriali.
La presente guida contiene le principali informazioni sull’organizzazione dei seguenti corsi:
Corso di Laurea di Primo Livello in Matematica
Corso di Laurea Specialistica in Matematica
Ulteriori aggiornamenti di questa guida saranno resi disponibili sul sito della Facoltà all’indirizzo:
www.scienzemfn.unisa.it
CORSO DI LAUREA DI PRIMO LIVELLO
IN MATEMATICA
(nuovo ordinamento)
• ASPETTI GENERALI
La durata normale del Corso di Laurea di Primo Livello è di tre anni. Il conseguimento della Laurea comporta
l’acquisizione di 180 Crediti Formativi Universitari distribuiti in media in numero pari a 60 per ogni anno.
Il Credito Formativo Universitario (CFU) è l’unità di misura del lavoro di apprendimento necessario allo studente per
l’espletamento delle attività formative prescritte per il conseguimento del titolo di studio. Ad un credito corrispondono
25 ore di lavoro di apprendimento comprensivo di ore di lezione, di esercitazione, di laboratorio, di seminario e di altre
attività formative, ivi comprese le ore di studio individuale.
• OBIETTIVI FORMATIVI
È obiettivo specifico del Corso di Laurea di Primo Livello in Matematica formare figure professionali che:
-
posseggano adeguate conoscenze di base nell'area della matematica;
posseggano competenze computazionali ed informatiche;
abbiano acquisito le metodiche disciplinari e siano in grado di comprendere e utilizzare descrizioni e modelli
matematici di situazioni concrete di interesse scientifico o economico;
siano in grado di utilizzare almeno una lingua dell'Unione Europea, oltre l'italiano, nell'ambito specifico di
competenza e per lo scambio di informazioni generali;
posseggano adeguate competenze e strumenti per la comunicazione e la gestione dell'informazione;
siano capaci di lavorare in gruppo, di operare con definiti gradi di autonomia e di inserirsi prontamente negli
ambienti di lavoro.
Ai fini indicati, i curricula del Corso di Laurea in Matematica
-
comprendono in ogni caso attività finalizzate a far acquisire:
le conoscenze fondamentali nei vari campi della matematica, nonché di metodi propri della matematica nel suo
complesso;
la modellizzazione di fenomeni naturali, sociali ed economici e di problemi tecnologici;
le tecniche di calcolo numerico e simbolico e gli aspetti computazionali della matematica e della statistica;
prevedono una quota significativa di attività formative caratterizzate da un particolare rigore logico e da un elevato
livello di astrazione;
prevedono, in relazione ad obiettivi specifici, l'obbligo di attività esterne, come tirocini formativi presso aziende,
strutture della pubblica amministrazione e laboratori, oltre a soggiorni di studio presso altre università italiane o
estere, anche nel quadro di accordi internazionali.
• AMBITI OCCUPAZIONALI PREVISTI PER I LAUREATI
I laureati in Matematica svolgeranno attività professionali nel campo della formazione e della diffusione della
cultura scientifica, nonché del supporto modellistico-matematico e computazionale ad attività dell'industria, della
finanza e della pubblica amministrazione.
• REQUISITI DI ACCESSO
Per accedere al Corso di Laurea di Primo Livello in Matematica è necessario essere in possesso di un diploma di
scuola secondaria superiore di durata quinquennale o di altro titolo di studio conseguito all’estero, riconosciuto idoneo
sulla base della normativa vigente.
Sono richieste preparazione culturale e adeguata conoscenza degli elementi di base della matematica normalmente
fornite dalla scuola media superiore.
L’adeguatezza di tale preparazione iniziale sarà valutata mediante un test di accesso non selettivo.
Saranno organizzati corsi di recupero per colmare eventuali lacune nella preparazione di base.
•
PROSEGUIMENTO DEGLI STUDI
Ai fini di un’eventuale prosecuzione di studi universitari, i 180 CFU acquisiti nel Corso di Laurea in Matematica
sono riconosciuti validi nella Laurea Specialistica in Matematica presso l’Università degli Studi di Salerno.
•
PIANO DIDATTICO
Le attività didattiche del Corso di Laurea di Primo Livello in Matematica saranno di norma organizzate in semestri,
con inizio il 1 Ottobre, con interruzione nel mese di febbraio e con temine nel mese di giugno. Agli studenti iscritti è
richiesta di norma la frequenza continuativa agli insegnamenti previsti nei rispettivi curricula di laurea.
Saranno previste di norma tre sessioni d'esami, nei mesi di febbraio, giugno-luglio e settembre. Nella sessione di
febbraio saranno previsti due appelli per gli insegnamenti del primo semestre, nella sessione di giugno-luglio saranno
previsti due appelli per gli insegnamenti del secondo semestre. Durante il periodo di svolgimento degli esami le lezioni
saranno sospese. L'acquisizione dei crediti avverrà al momento dell'esame, che darà luogo anche a valutazione in
trentesimi.
Per l’anno accademico 2006/2007 è previsto il seguente calendario:
Lezioni
Semestre
Primo
Secondo
Data di inizio
2 ottobre 2006
5 marzo 2007
Data di fine
26 gennaio 2007
8 giugno 2007
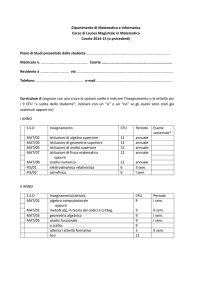
• ELENCO DEGLI INSEGNAMENTI E DELLE ALTRE ATTIVITÀ FORMATIVE
Sono insegnamenti comuni a tutti i curricula:
Anno di corso/
semestre
1/1
Denominazione
Settore
Crediti
Matematica di Base
MAT/02
3
1/1
Analisi Matematica I
MAT/05
8
1/1
Geometria I
MAT/03
8
1/1
Fondamenti di Informatica e
INF/01
6
Laboratorio
1/1
Lingua Straniera
3
1/2
Algebra I
MAT/02
8
1/2
Analisi Matematica II
MAT/05
8
1/2
Geometria II
MAT/03
7
1/2
Laboratorio di
MAT/08
9
Programmazione e Calcolo
2/1
Algebra II
MAT/02
6
2/1
Analisi Matematica III
MAT/05
6
2/1
Geometria III
MAT/03
6
2/1
Logica Matematica I
MAT/01
6
2/1
Lingua Straniera
2/2
Analisi Matematica IV
MAT/05
6
2/2
Calcolo Numerico
MAT/08
6
2/2
Fisica Generale I
FIS/01
6
2/2
Laboratorio di Fisica Generale I
FIS/01
3
2/2
Teoria dell'Informazione
INF/01
6
3/1
Fisica Matematica I
MAT/07
6
3/1
Fisica Generale II
FIS/01
6
3/1
Laboratorio di
FIS/01
3
3
Fisica Generale II
Scelta autonoma
9
Altre attività
9
Prova finale
3
I rimanenti insegnamenti, per un totale di 30 crediti, dipendono dal curriculum scelto.
• Curricula offerti agli studenti
I curricula della laurea di Primo Livello in Matematica sono i seguenti: “Matematica ad indirizzo generale”,
“Matematica per il trattamento dell'informazione”, “Matematica per la didattica, la formazione e la divulgazione
scientifica”, “Matematica per le applicazioni all'industria e alla tecnologia”.
Curriculum Matematica ad indirizzo generale
Il curriculum “Matematica ad indirizzo generale” si prefigge di fornire approfondite conoscenze di base nell'area della
matematica ed un elevato livello di astrazione e di autonomia nella risoluzione dei problemi.
I crediti acquisiti nel percorso comune dovranno essere completati nel modo seguente:
Anno di
Denominazione
Settore
Crediti
3/
Un insegnamento del gruppo A
MAT/
6
3/
Un insegnamento del gruppo A
MAT/
6
3/
Un insegnamento del gruppo A
MAT/
6
3/
Un insegnamento del gruppo A
MAT/
6
3/
Un insegnamento del gruppo A
MAT/
6
Denominazione
Settore
Crediti
3/
Algebra III
MAT/02
6
3/
Algebra IV
MAT/02
6
3/
Analisi Matematica V
MAT/05
6
3/
Analisi Matematica VI
MAT/05
6
3/
Equazioni Differenziali
MAT/05
6
3/
Fisica Matematica II
MAT/07
6
3/
Geometria IV
MAT/03
6
3/
Geometria V
MAT/03
6
3/
Geometria VI
MAT/03
6
3/
Teoria della Computabilità I
MAT/01
6
corso/semestre
Gruppo A
Anno di
corso/semestre
Curriculum Matematica per il trattamento dell’informazione
Il curriculum “Matematica per il trattamento dell’informazione” si prefigge di fornire un’elevata conoscenza pratica e
teorica degli strumenti matematici fondamentali per l’informatica con particolare riferimento al trattamento
dell’informazione di natura numerica e simbolica.
I crediti acquisiti nel percorso comune dovranno essere completati nel modo seguente:
Anno di
Denominazione
Settore
Crediti
2/2
Teoria della Computabilità I
MAT/01
6
3/
Un insegnamento del gruppo B
corso/semestre
(o due moduli)
6
3/
Un insegnamento del gruppo C
6
(o due moduli)
3/
Un insegnamento del gruppo C
6
(o due moduli)
3/
Un insegnamento matematico
6
(o due moduli)
(scelto tra gli insegnamenti
attivati in uno dei settori
inizianti con la sigla
MAT/)
Gruppo B
Anno di
Denominazione
Settore
Crediti
Calcolo delle Probabilità e
MAT/06
3
corso/semestre
3/
Statistica
3/
Logica Matematica II
MAT/01
6
3/
Semigruppi Liberi e
MAT/02
3
Teoria dei Codici
3/
Teoria dei Grafi
MAT/03
3
3/
Fisica dell’Informazione
FIS/02
3
Denominazione
Settore
Crediti
3/
Calcolo Numerico II
MAT/08
6
3/
Geometria Combinatoria
MAT/03
3
3/
Teoria dei Giochi
MAT/05
3
3/
Teoria delle Funzioni
MAT/05
6
3/
Data Base
INF/01
6
3/
Intelligenza Artificiale
INF/01
3
3/
Linguaggi di Programmazione
INF/01
3
3/
Metodi per il Trattamento
INF/01
6
Gruppo C
Anno di
corso/semestre
dell’Informazione
Insegnamenti di matematica attivati nell’a.a. 2006/2007
3/
3/
3/
3/
3/
3/
3/
Algebra III
Algebra IV
Analisi Funzionale I
Analisi Matematica V
Analisi Matematica VI
Analisi Numerica
Calcolo delle Probabilità
e Statistica
Calcolo Numerico II
Equazioni Differenziali
Fisica Matematica II
Fondamenti di
Geometria
Geometria IV
Geometria V
Geometria VI
Laboratorio di
Matematica
Computazionale
Logica Matematica II
Matematiche
Complementari I
Matematiche
Complementari II
Matematiche Elementari
da un punto di vista
superiore
Ricerca Operativa
Semigruppi Liberi e
Teoria dei Codici
Storia delle
Matematiche
Teoria dei Grafi
Teoria dei Numeri
Teoria delle Funzioni
3/
3/
3/
3/
3/
3/
3/
3/
3/
3/
3/
3/
3/
3/
3/
3/
3/
3/
MAT/02
MAT/02
MAT/05
MAT/05
MAT/05
MAT/08
MAT/06
6
6
6
6
6
6
3
MAT/08
MAT/05
MAT/07
MAT/03
6
6
6
3
MAT/03
MAT/03
MAT/03
MAT/08
6
6
6
3
MAT/01
MAT/04
6
6
MAT/04
6
MAT/04
6
MAT/09
MAT/02
6
3
MAT/04
6
MAT/03
MAT/02
MAT/05
3
3
6
Potranno inoltre essere scelti tutti gli insegnamenti di Matematica attivati nella Laurea Specialistica.
Curriculum Matematica per la didattica, la formazione e la divulgazione scientifica
Il curriculum “Matematica per la didattica, la formazione e la divulgazione scientifica” si prefigge di fornire
competenze relative alla storia ed alla epistemologia della matematica, nonché competenze della metodologia di
trasmissione della conoscenza scientifica.
I crediti acquisiti nel percorso comune dovranno essere completati nel modo seguente:
Anno di
Denominazione
Settore
Crediti
2/2
Matematiche Complementari I
MAT/04
6
3/
Un insegnamento del gruppo
MAT/
6
D
o CHIM/03
Un insegnamento del gruppo
MAT/
corso/semestre
3/
D
6
3/
Un insegnamento del gruppo
MAT/
6
MAT/
6
Denominazione
Settore
Crediti
3/
Algebra III
MAT/02
6
3/
Analisi Funzionale I
MAT/05
6
3/
Fondamenti di Geometria
MAT/03
3
3/
Matematiche Complementari II
MAT/04
6
3/
Matematiche Elementari da un
MAT/04
6
D
(o due moduli)
3/
Un insegnamento matematico
(o due moduli)
(scelto tra gli insegnamenti
attivati in uno dei settori
inizianti con la sigla
MAT/)
Gruppo D
Anno di
corso/semestre
punto di vista superiore
3/
Storia delle Matematiche
MAT/04
6
3/
Teoria dei Numeri
MAT/02
3
3/
Chimica
CHIM/03
6
Insegnamenti di matematica attivati nell’a.a. 2006/2007
3/
3/
3/
3/
3/
3/
3/
3/
3/
3/
3/
3/
3/
3/
3/
Algebra III
Algebra IV
Analisi Funzionale I
Analisi Matematica V
Analisi Matematica VI
Analisi Numerica
Calcolo delle Probabilità
e Statistica
Calcolo Numerico II
Equazioni Differenziali
Fisica Matematica II
Fondamenti di
Geometria
Geometria IV
Geometria V
Geometria VI
Laboratorio di
Matematica
Computazionale
MAT/02
MAT/02
MAT/05
MAT/05
MAT/05
MAT/08
MAT/06
6
6
6
6
6
6
3
MAT/08
MAT/05
MAT/07
MAT/03
6
6
6
3
MAT/03
MAT/03
MAT/03
MAT/08
6
6
6
3
3/
3/
Logica Matematica II
Matematiche
Complementari II
Matematiche Elementari
da un punto di vista
superiore
Ricerca Operativa
Semigruppi Liberi e
Teoria dei Codici
Storia delle
Matematiche
Teoria dei Grafi
Teoria dei Numeri
Teoria della
Computabilità I
Teoria delle Funzioni
3/
3/
3/
3/
3/
3/
3/
3/
MAT/01
MAT/04
6
6
MAT/04
6
MAT/09
MAT/02
6
3
MAT/04
6
MAT/03
MAT/02
MAT/01
3
3
6
MAT/05
6
Potranno inoltre essere scelti tutti gli insegnamenti di Matematica attivati nella Laurea Specialistica.
Curriculum Matematica per le applicazioni all'industria e alla tecnologia
Il curriculum “Matematica per le applicazioni all'industria e alla tecnologia” si prefigge di fornire un’elevata capacità
di trattamento di informazioni di carattere non solo numerico, nonché un’alta competenza teorica e pratica delle
strutture di calcolo.
I crediti acquisiti nel percorso comune dovranno essere completati nel seguente modo:
Anno di
Denominazione
Settore
Crediti
2/2
Teoria della Computabilità I
MAT/01
6
3/
Un insegnamento del gruppo E
6
3/
Un insegnamento del gruppo E
6
3/
Un insegnamento del gruppo E
6
3/
Un insegnamento matematico
corso/semestre
MAT/
6
Denominazione
Settore
Crediti
3/
Analisi Numerica
MAT/08
6
3/
Fisica Matematica II
MAT/07
6
3/
Ricerca Operativa
MAT/09
6
(o due moduli)
(scelto tra gli insegnamenti
attivati in uno dei settori
inizianti con la sigla
MAT/)
Gruppo E
Anno di
corso/semestre
3/
Simulazione
INF/01
6
3/
Teoria dell’Informazione II
INF/01
6
Insegnamenti di matematica attivati nell’a.a. 2006/2007
3/
3/
3/
3/
3/
3/
3/
3/
3/
3/
3/
3/
3/
3/
3/
3/
3/
3/
3/
3/
3/
3/
3/
3/
3/
Algebra III
Algebra IV
Analisi Funzionale I
Analisi Matematica V
Analisi Matematica VI
Analisi Numerica
Calcolo delle Probabilità
e Statistica
Calcolo Numerico II
Equazioni Differenziali
Fisica Matematica II
Fondamenti di
Geometria
Geometria IV
Geometria V
Geometria VI
Laboratorio di
Matematica
Computazionale
Logica Matematica II
Matematiche
Complementari I
Matematiche
Complementari II
Matematiche Elementari
da un punto di vista
superiore
Ricerca Operativa
Semigruppi Liberi e
Teoria dei Codici
Storia delle
Matematiche
Teoria dei Grafi
Teoria dei Numeri
Teoria delle Funzioni
MAT/02
MAT/02
MAT/05
MAT/05
MAT/05
MAT/08
MAT/06
6
6
6
6
6
6
3
MAT/08
MAT/05
MAT/07
MAT/03
6
6
6
3
MAT/03
MAT/03
MAT/03
MAT/08
6
6
6
3
MAT/01
MAT/04
6
6
MAT/04
6
MAT/04
6
MAT/09
MAT/02
6
3
MAT/04
6
MAT/03
MAT/02
MAT/05
3
3
6
Potranno inoltre essere scelti tutti gli insegnamenti di Matematica attivati nella Laurea Specialistica.
INSEGNAMENTI ATTIVATI PER L’ANNO ACCADEMICO 2006/2007
I ANNO - I SEMESTRE
Matematica di Base (3 CFU)
Analisi Matematica I (8 CFU)
Geometria I (8 CFU)
Fondamenti di Informatica e
Laboratorio (6 CFU)
Prof. G. Vincenzi
Prof.ssa M. Transirico
Dott.ssa P. Cavaliere
Prof. G. Sparano
Prof. D. Parente
I ANNO - II SEMESTRE
Algebra I (8 CFU)
Analisi Matematica II (8 CFU)
Geometria II (7 CFU)
Laboratorio di Programmazione e
Calcolo (9 CFU)
II ANNO - I SEMESTRE
Algebra II (6 CFU)
Analisi Matematica III (6 CFU)
Geometria III (6 CFU)
Logica Matematica I (6 CFU)
II ANNO-II SEMESTRE
CURRICULUM
Analisi Matematica IV (6 CFU)
Calcolo Numerico
Fisica Generale I (6 CFU)
Matematica ad Indirizzo Laboratorio di Fisica Generale I
Generale
(3 CFU)
Teoria dell’Informazione (6 CFU)
II ANNO-II SEMESTRE
Analisi Matematica IV (6 CFU)
CURRICULUM
Matematica per il
Trattamento
dell’Informazione
Calcolo Numerico
Fisica Generale I (6 CFU)
Laboratorio di Fisica Generale I
(3 CFU)
Teoria dell’Informazione (6 CFU)
Teoria della Computabilità I (6 CFU)
II ANNO-II SEMESTRE
Analisi Matematica IV (6 CFU)
CURRICULUM
Calcolo Numerico
Matematica per la
Didattica, la Formazione e Fisica Generale I (6 CFU)
la Divulgazione
Scientifica
Laboratorio di Fisica Generale I
(3 CFU)
Teoria dell’Informazione (6 CFU)
Matematiche Complementari I
(6 CFU)
II ANNO-II SEMESTRE
Analisi Matematica IV (6 CFU)
CURRICULUM
Matematica per le
Applicazioni all’Industria
e alla Tecnologia
Calcolo Numerico
Fisica Generale I (6 CFU)
Laboratorio di Fisica Generale I
(3 CFU)
Teoria dell’Informazione (6 CFU)
Teoria della Computabilità I (6 CFU)
Prof.ssa M. Maj
Dott.ssa C. Nicotera
Prof.ssa M. Transirico
Dott.ssa P. Cavaliere
Prof. G. Sparano
Dott. G. Capobianco
Prof.ssa P. Longobardi
Dott. C. Delizia
Prof.ssa L. Sgambati
Dott.ssa S. Monsurrò
Prof.ssa A. Di Concilio
Dott.ssa A. Miranda
Prof. A. Di Nola
Prof.ssa L. Sgambati
Dott.ssa S. Monsurrò
Prof.ssa B. Paternoster
Dott.ssa D. Conte
Prof. M. Fusco Girard
Dott. G. Lambiase
Prof. C. Attanasio
Prof.ssa V. Giorno
Prof.ssa L. Sgambati
Dott.ssa S. Monsurrò
Prof.ssa B. Paternoster
Dott.ssa D. Conte
Prof. M. Fusco Girard
Dott. G. Lambiase
Prof. C. Attanasio
Prof.ssa V. Giorno
Prof. G. Gerla
Prof.ssa L. Sgambati
Dott.ssa S. Monsurrò
Prof.ssa B. Paternoster
Dott.ssa D. Conte
Prof. M. Fusco Girard
Dott. G. Lambiase
Prof. C. Attanasio
Prof.ssa V. Giorno
Prof. F. Palladino
Prof.ssa L. Sgambati
Dott.ssa S. Monsurrò
Prof.ssa B. Paternoster
Dott.ssa D. Conte
Prof. M. Fusco Girard
Dott. G. Lambiase
Prof. C. Attanasio
Prof.ssa V. Giorno
Prof. G. Gerla
III ANNO-I SEMESTRE Fisica Matematica I (6 CFU)
Fisica Generale II (6 CFU)
Laboratorio di Fisica Generale II
Prof. E. Laserra
Prof. M. Fusco Girard
Dott. G. Lambiase
Sono inoltre attivati i seguenti insegnamenti :
III ANNO - I SEMESTRE
Algebra IV (6 CFU)
Analisi Funzionale I (6 CFU)
Analisi Matematica V (6 CFU)
Fondamenti di Geometria (3 CFU)
Geometria IV (6 CFU)
Matematiche Complementari II
(6 CFU)
Matematiche Elementari da un punto
di vista superiore (6 CFU)
Metodi per il Trattamento
dell’Informazione (6 CFU)
Storia delle Matematiche (6 CFU)
Teoria dell’Informazione II (6 CFU)
Teoria dei Grafi (3 CFU)
Prof.ssa M. Maj
Prof.ssa L. Sgambati
Prof. A. Vitolo
Prof. F. Bottacin
Prof. A. Vinogradov
Prof. G. Gerla
Prof. F. Palladino
Prof.ssa V. Giorno
Prof. F. Palladino
Prof.ssa V. Giorno
Prof. F. Bottacin
III ANNO - II SEMESTRE
Algebra III (6 CFU)
Analisi Matematica VI (6 CFU)
Analisi Numerica (6 CFU) (mutuato
con Calcolo Numerico II)
Calcolo delle Probabilità e Statistica
(3 CFU)
Calcolo Numerico II (6 CFU)
Equazioni Differenziali (6 CFU)
Fisica Matematica II (6 CFU)
Geometria V (6 CFU)
Geometria VI (6 CFU)
Laboratorio di Matematica
Computazionale (3 CFU)
Linguaggi di Programmazione
(3 CFU)
Logica Matematica II (6 CFU)
Matematiche Complementari I
(6 CFU)
Ricerca Operativa
Semigruppi Liberi e Teoria dei Codici
(3 CFU)
Teoria dei Numeri (3 CFU)
Teoria della Computabilità I (6 CFU)
Teoria delle Funzioni (6 CFU)
Prof. G. Vincenzi
Prof. A. Vitolo
Prof. A. Di Crescenzo
Prof.ssa E. Russo
Prof.ssa A. Canale
Prof. E. Laserra
Prof. A. Vinogradov
Prof.ssa A. Di Concilio
Dott.ssa D. Conte
Prof.ssa M. Napoli
Prof. G. Gerla
Prof. F. Palladino
Prof. R. Cerulli
Dott.ssa M. Gentili
Prof.ssa P. Longobardi
Prof.ssa P. Longobardi
Prof. G. Gerla
Prof. V. Cafagna
nonché tutti gli insegnamenti attivati nella Laurea Specialistica in Matematica.
• VERIFICA DELLA CONOSCENZA DI UNA LINGUA DELL’UNIONE EUROPEA OLTRE L’ITALIANO
Sono previste due prove di verifica della conoscenza della lingua inglese. Ciascuna prova permetterà di acquisire 3
CFU, non è prevista valutazione in trentesimi.
• RICONOSCIMENTO IN CREDITI DI ABILITA’ E CONOSCENZE
Il Consiglio di Area Didattica può riconoscere come CFU conoscenze e abilità professionali certificate ai sensi della
normativa vigente in materia, nonché altre conoscenze e abilità maturate in attività formative di livello post-secondario
alla cui progettazione e realizzazione l’Università abbia concorso, secondo quanto previsto dalla normativa vigente.
• TIROCINIO/STAGE
L’attività di tirocinio può essere svolta sia all’esterno dell’Università presso Aziende, Scuole ed Enti pubblici o
privati, sia all’interno dell’Università presso i Laboratori Specialistici del Dipartimento di Matematica e Informatica.
Il modulo per la richiesta di assegnazione tirocinio va ritirato e consegnato presso l’Ufficio Tirocinio/Stage della
Segreteria di Presidenza della Facoltà di Scienze MM.FF.NN..
• PROVA FINALE
Acquisiti i necessari 177 crediti formativi, lo studente è ammesso a sostenere la prova finale per il conseguimento
del titolo.
La prova finale, che consente di acquisire i restanti 3 crediti, consiste di norma nella discussione, dinanzi ad una
Commissione, secondo quanto previsto dal Regolamento didattico di Facoltà, di un elaborato scritto preparato dallo
studente e dà luogo al voto finale di laurea, espresso in centodecimi.
La valutazione conclusiva terrà conto dell’intera carriera dello studente all’interno del corso di studi, dei tempi e
delle modalità di acquisizione dei crediti formativi, delle valutazioni sulle attività formative e sulla prova finale.
In particolare il voto di laurea sarà calcolato come la somma di:
la media ponderata espressa in centodecimi calcolata in base ai crediti dei voti di ogni singola attività formativa
(con eccezione delle attività formative con idoneità),
- il voto della prova finale che di norma non potrà superare i sette punti,
punti calcolati in base alla qualità degli studi effettuati ed in base al tempo impiegato per concludere gli studi
calcolato dalla prima immatricolazione (fino a un massimo di tre punti).
• TUTORATO
Il tutorato si propone di contribuire all’orientamento degli studenti nel corso degli studi, migliorando le condizioni di
apprendimento e riducendo i tassi di abbandono.
All’atto dell’iscrizione ciascuno studente viene affidato ad un tutore secondo modalità precisate ogni anno sulla Guida
dello Studente. Per l’anno accademico 2006/2007 l’associazione studente-tutore è determinata dal resto della divisione
della matricola dello studente per 29 e dalla consultazione della seguente tabella.
TUTORE
Annunziato M.
Bottacin F.
Cafagna V.
Canale A.
Caso L.
Cavaliere P.
Conte D.
Delizia C.
Di Concilio A.
Di Crescenzo A.
Di Gironimo P.
Di Nola A.
Esposito L.
Gerla G.
Giorno V.
RESTO
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Laserra E.
Longobardi P.
Maj M.
Miranda A.
Monsurrò S.
Nicotera C.
Palladino F.
Paternoster B.
Sgambati L.
Sparano G.
Transirico M.
Vincenzi G.
Vinogradov A.
Vitolo A.
15
16
17
18
19
20
21
22
23
24
25
26
27
28
Agli studenti il cui tutore è per qualche motivo indisponibile viene effettuata una nuova assegnazione con modalità
stabilite dal Presidente del Consiglio di Corso di Laurea. Il tutore dovrà fornire informazioni sul corso di laurea, seguire
da vicino l'attività di studio dello studente affidatogli, assisterlo nella elaborazione del piano di studi e nella scelta della
tesi di laurea.
Gli studenti sono invitati a relazionare al proprio tutore, almeno due volte l'anno, sul proprio iter di studio.
CORSO DI LAUREA SPECIALISTICA
IN MATEMATICA
( nuovo ordinamento)
• ASPETTI GENERALI
Il conseguimento della Laurea Specialistica in Matematica comporta l’acquisizione di 300 Crediti Formativi
Universitari (CFU) (di cui 180 già conseguiti nella Laurea di Primo Livello).
• OBIETTIVI FORMATIVI SPECIFICI
I laureati nel Corso di Laurea Specialistica in Matematica devono:
- avere una solida preparazione culturale nell’area della matematica e dei metodi propri della disciplina;
- conoscere approfonditamente il metodo scientifico;
- possedere avanzate competenze computazionali ed informatiche;
- avere conoscenze matematiche specialistiche, anche contestualizzate ad altre scienze, all’ingegneria e ad altri
campi applicativi;
- essere in grado di analizzare e risolvere problemi complessi, anche in contesti applicativi;
- essere in grado di riconoscere e di costruire i diversi modelli matematici nelle applicazioni scientifiche,
industriali ed economiche;
- aver acquisito specifiche capacità per la comunicazione dei problemi e dei metodi della matematica;
- essere in grado di utilizzare fluentemente, in forma scritta e orale, almeno una lingua dell'Unione Europea oltre
l'italiano con riferimento anche ai lessici disciplinari;
- avere capacità relazionali e decisionali, ed essere capaci di lavorare con ampia autonomia, anche assumendo
responsabilità scientifiche ed organizzative.
Ai fini indicati, il curriculum del Corso di Laurea Specialistica in Matematica comprende:
attività formative che si caratterizzano per un particolare rigore logico e per un livello elevato di astrazione;
- attività di laboratorio computazionale e informatico, in particolare dedicate alla conoscenza di applicazioni
informatiche, ai linguaggi di programmazione e al calcolo;
attività esterne, in relazione a obiettivi specifici, come tirocini formativi presso aziende e laboratori e
soggiorni di studio presso altre università italiane ed europee, anche nel quadro di accordi internazionali.
• AMBITI OCCUPAZIONALI PREVISTI PER I LAUREATI
I laureati del Corso di Laurea Specialistica in Matematica potranno esercitare funzioni di elevata responsabilità nella
costruzione e nello sviluppo computazionale di modelli matematici di varia natura, in diversi ambiti applicativi
scientifici, ambientali, sanitari, industriali, finanziari, nei servizi e nella pubblica amministrazione, nei settori della
comunicazione della matematica e della scienza.
• REQUISITI DI ACCESSO
Per essere ammessi al Corso di Laurea Specialistica in Matematica occorre essere in possesso di una laurea di primo
livello conseguita presso una Facoltà di Scienze Matematiche Fisiche e Naturali, presso una Facoltà di Ingegneria, o
presso facoltà di natura scientifica ritenute affini dal Consiglio di Corso di Laurea, o di altro titolo conseguito
all’estero riconosciuto idoneo ai sensi delle leggi vigenti e nelle forme previste dall’art. 17 del Regolamento Didattico
di Ateneo, per il quale il Consiglio di Corso di Laurea riconosca l’idoneità.
Agli studenti che hanno conseguito la Laurea di Primo Livello in Matematica vengono riconosciuti tutti i 180 crediti.
I rimanenti 120 crediti saranno così suddivisi:
• 16 crediti di insegnamenti non di matematica, a scelta tra i seguenti
Elementi di Fisica Moderna
Chimica
Data Base
Intelligenza Artificiale
Linguaggi di
Programmazione
Metodi per il Trattamento
dell’Informazione
Simulazione
Teoria dell’Informazione II
FIS/01
CHIM/03
INF/01
INF/01
INF/01
4
6
6
3
3
INF/01
6
INF/01
INF/01
6
6
nonché tra tutti gli insegnamenti dei settori INF/01, FIS/01, FIS/02, CHIM/03 attivati in Facoltà;
• 6 crediti a scelta dello studente;
• 27 crediti per la prova finale;
• 71 crediti di insegnamenti di matematica, di cui almeno 6 nei settori MAT/01 o MAT/04, almeno 7 nei settori
MAT/02 o MAT/03, almeno 6 nel settore MAT/05, almeno 3 nei settori MAT/07 o MAT/08.
Complessivamente i 300 crediti necessari per conseguire la Laurea Specialistica in Matematica dovranno
prevedere, oltre agli insegnamenti già obbligatori per tutti i percorsi nella Laurea di Primo Livello in
Matematica, almeno
CFU
Settore
DENOMINAZIONE
6
MAT/02
Algebra
12
MAT/05
Analisi Matematica
6
MAT/08
Analisi Numerica
6
MAT/07
Fisica Matematica
9
MAT/03
Geometria
6
MAT/01
Logica Matematica
3
MAT/04
Matematiche Complementari
Gli insegnamenti di matematica potranno essere scelti tra i seguenti:
Denominazione
Settore
CFU
Algebra III
Algebra IV
Algebra Universale e
Teoria dei Modelli
Analisi Funzionale I
Analisi Funzionale II
Analisi Matematica V
Analisi Matematica VI
Analisi Numerica (avanzata)
Analisi Superiore
Calcolo delle Probabilità e
Statistica
Calcolo Numerico II
Equazioni Differenziali
Fisica Matematica II
Fondamenti di Geometria
Geometria IV
Geometria V
Geometria VI
Geometria Algebrica
Istituzioni di Fisica Matematica
Laboratorio di Matematica
Computazionale
Logica Matematica I
Logica Matematica II
Matematiche Complementari I
Matematiche Complementari II
Matematiche Elementari da un
punto di vista superiore
Ricerca Operativa
Semigruppi Liberi e
Teoria dei Codici
Statistica Matematica
Storia delle Matematiche
Teoria dei Grafi
Teoria dei Gruppi
Teoria dei Numeri
Teoria della Computabilità I
Teoria delle Funzioni
Topologia
MAT/02
MAT/02
MAT/01
6
6
6
MAT/05
MAT/05
MAT/05
MAT/05
MAT/08
MAT/05
MAT/06
6
3+3
6
6
6
6
3
MAT/08
MAT/05
MAT/07
MAT/03
MAT/03
MAT/03
MAT/03
MAT/03
MAT/07
MAT/08
6
6
6
3
6
6
6
3
6
3
MAT/01
MAT/01
MAT/04
MAT/04
MAT/04
6
6
6
6
6
MAT/09
MAT/02
6
3
MAT/06
MAT/04
MAT/03
MAT/02
MAT/02
MAT/01
MAT/05
MAT/03
3
6
3
6
3
6
6
6
Nell’a.a. 2006/2007 sono attivati i seguenti insegnamenti:
I SEMESTRE
Algebra IV (6 CFU)
Analisi Funzionale I (6 CFU)
Prof.ssa M. Maj
Prof.ssa L. Sgambati
Analisi Matematica V (6 CFU)
Analisi Superiore (6 CFU)
Fondamenti di Geometria (3 CFU)
Geometria IV (6 CFU)
Logica Matematica I (6 CFU)
Matematiche Complementari II
(6 CFU)
Matematiche Elementari da un punto
di vista superiore (6 CFU)
Metodi per il Trattamento
dell’Informazione (6 CFU)
Storia delle Matematiche (6 CFU)
Teoria dei Grafi (3 CFU)
Teoria dell’Informazione II
Prof. A. Vitolo
Prof.ssa M. Transirico
Prof. F. Bottacin
Prof. A. Vinogradov
Prof. A. Di Nola
Prof. G. Gerla
Prof. F. Palladino
Prof.ssa V. Giorno
Prof. F. Palladino
Prof. F. Bottacin
Prof.ssa V. Giorno
II SEMESTRE
Algebra III (6 CFU)
Algebra Universale e
Teoria dei Modelli (6 CFU)
Analisi Funzionale II (3+3 CFU)
Analisi Matematica VI (6 CFU)
Analisi Numerica (avanzata) (6 CFU)
Calcolo delle Probabilità e Statistica
(3 CFU)
Calcolo Numerico II (6 CFU)
Elementi di Fisica Moderna (4 CFU)
Equazioni Differenziali (6 CFU)
Fisica Matematica II (6 CFU)
Geometria V (6 CFU)
Geometria VI (6 CFU)
Geometria Algebrica (3CFU)
Istituzioni di Fisica Matematica
(6 CFU)
Laboratorio di Matematica
Computazionale (3 CFU)
Linguaggi di Programmazione (3CFU)
Logica Matematica II (6 CFU)
Matematiche Complementari I
(6 CFU)
Ricerca Operativa (6 CFU)
Semigruppi Liberi e Teoria dei Codici
(3 CFU)
Statistica Matematica (3 CFU)
Teoria dei Gruppi (6CFU)
Teoria dei Numeri (3 CFU)
Teoria della Computabilità I (6 CFU)
Teoria delle Funzioni (6 CFU)
Topologia (6 CFU)
Prof. G. Vincenzi
Prof. A. Di Nola
Prof.ssa L. Sgambati
Prof. A. Vitolo
Prof.ssa E. Russo
Prof. A. Di Crescenzo
Prof.ssa E. Russo
Prof. M. Fusco Girard
Prof.ssa A. Canale
Prof. E. Laserra
Prof. A. Vinogradov
Prof.ssa A. Di Concilio
Prof. F. Bottacin
Prof. E. Laserra
Dott.ssa D.Conte
Prof.ssa M. Napoli
Prof. G. Gerla
Prof. F. Palladino
Prof. R. Cerulli
Dott.ssa M. Gentili
Prof.ssa P. Longobardi
Prof. A. Di Crescenzo
Prof.ssa M.Maj
Prof.ssa P. Longobardi
Prof. G. Gerla
Prof. V. Cafagna
Prof.ssa A. Di Concilio
Piani di studio che non rispettino le norme precedenti saranno esaminati volta per volta dal Consiglio di Area
Didattica.
• ORGANIZZAZIONE DELLE ATTIVITA’ DIDATTICHE
L’attività didattica del Corso di Laurea Specialistica in Matematica è organizzata in modo da richiedere annualmente
allo studente 1500 ore di apprendimento, di cui almeno 1000 sono riservate allo studio personale o ad altre attività di
tipo individuale.
Le attività didattiche del Corso di Laurea Specialistica in Matematica saranno di norma organizzate in semestri, con
inizio il 1 Ottobre, con interruzione nel mese di febbraio e con temine nel mese di giugno. Agli studenti iscritti è
fortemente consigliata la frequenza alle lezioni.
Per l’anno accademico 2006/2007 è previsto il seguente calendario:
Semestre
Primo
Secondo
Data di inizio
2 ottobre 2006
5 marzo 2007
Data di fine
26 gennaio 2007
8 giugno 2007
• DISPOSIZIONI SUGLI OBBLIGHI DI FREQUENZA
Per gli studenti iscritti è fortemente consigliata la frequenza.
• TIPOLOGIA E MODALITA’ DI SVOLGIMENTO DEGLI ESAMI E DELLE ALTRE PROVE DI
VERIFICA DEL PROFITTO
Gli esami e le prove di verifica sono attività volte ad accertare il grado di preparazione degli studenti. Potranno
essere orali e/o scritti, o consistere in prove pratiche o in stesura di tesine. L'acquisizione dei crediti avverrà al momento
della prova, che, nel caso degli esami, darà luogo anche a valutazione in trentesimi.
Esami e prove di verifica si svolgeranno secondo le modalità previste dal Regolamento didattico di Ateneo e dal
Regolamento didattico di Facoltà, in date anteriormente pubblicizzate secondo quanto deliberato nell’annuale
programmazione didattica.
Saranno previste di norma tre sessioni d'esami, nei mesi di febbraio (sono previsti due appelli per gli insegnamenti
del primo semestre), giugno-luglio (sono previsti due appelli per gli insegnamenti del secondo semestre) e settembre.
Durante il periodo di svolgimento degli esami le lezioni saranno sospese.
• PROVA FINALE
La prova finale consisterà nella discussione, dinanzi ad una Commissione, secondo quanto previsto dal Regolamento
didattico di Facoltà, di un elaborato scritto in cui lo studente dia prova di autonomia e padronanza dell’argomento
trattato, e darà luogo al voto finale di laurea, espresso in centodecimi.
La valutazione conclusiva terrà conto dell’intera carriera dello studente all’interno del corso di studi, dei tempi e
delle modalità di acquisizione dei crediti formativi, delle valutazioni sulle attività formative e sulla prova finale.
In particolare il voto di laurea sarà calcolato come la somma di:
la media ponderata espressa in centodecimi calcolata in base ai crediti dei voti di ogni singola attività formativa,
- il voto della prova finale che di norma non potrà superare i cinque punti,
punti calcolati in base alla qualità degli studi effettuati ed in base al tempo impiegato per concludere gli studi
calcolato dalla prima immatricolazione (fino a un massimo di due punti).
PROGRAMMI DEL CORSO DI LAUREA
DI PRIMO LIVELLO IN MATEMATICA
ALGEBRA I
Prof.ssa Mercede Maj
Obiettivi formativi
Scopo di questo corso è lo studio delle strutture algebriche, e, in particolare, di alcune strutture notevoli quali i gruppi,
gli anelli, gli spazi vettoriali.
Contenuti del corso
Numeri interi, congruenze.
Cardinalità di insiemi, insiemi finiti ed infiniti.
Strutture Algebriche: esempi, sottostrutture, congruenze, omomorfismi tra strutture.
Gruppi: esempi, gruppi di permutazioni, gruppi di matrici, sottogruppi, sottogruppo generato, teorema di Lagrange,
congruenze in un gruppo e gruppo quoziente, omomorfismi tra gruppi, teorema di Cayley, gruppi ciclici, periodo di un
elemento, prodotti diretti.
Anelli: esempi, anelli di polinomi, sottoanelli ed ideali, teorema di Krull, anello quoziente, omomorfismi, caratteristica
di un anello unitario, campo dei quozienti di un dominio d’integrità.
Spazi Vettoriali: esempi, sottospazi, quozienti, omomorfismi, basi di uno spazio vettoriale, dimensione, sottospazi
supplementari, spazi vettoriali di dimensione finita.
Testi consigliati
M. CURZIO, P. LONGOBARDI, M. MAJ - Lezioni di Algebra - Liguori Editore, Napoli, 1994.
M. CURZIO, P. LONGOBARDI, M. MAJ - Esercizi di Algebra – Una raccolta di prove d’esame svolte - Liguori
Editore, Napoli, 1995.
Modalità di valutazione
Prova scritta e prova orale.
ALGEBRA II
Prof.ssa Patrizia Longobardi
Obiettivi formativi
Scopo di questo corso è completare lo studio di proprietà notevoli relative ad anelli e a spazi vettoriali, e approfondire
lo studio dei polinomi e dei campi. Vengono inoltre illustrati primi elementi della teoria di Galois.
Contenuti del corso
Anelli: richiami, anello degli endomorfismi di un gruppo abeliano, radicale e nilradicale di un anello. Anelli fattoriali,
anelli principali, anelli euclidei.
Spazi vettoriali: richiami, spazi vettoriali isomorfi, somme dirette di sottospazi, struttura additiva di uno spazio
vettoriale e di un corpo.
Polinomi: richiami sulle radici di un polinomio, sulle radici semplici, multiple. Polinomi primitivi, polinomi su di un
anello fattoriale. Teorema della base di Hilbert.
Teoria dei campi: elementi algebrici e trascendenti, estensioni algebriche e trascendenti, estensioni simboliche.
Chiusura algebrica di un sottocampo in un campo, teorema di Cantor. Campi algebricamente chiusi. Campo di
spezzamento di un polinomio. Teoremi di prolungamento. Radici dell’unità. Campi finiti.
Teoria di Galois: gruppo di Galois di un'estensione e di un polinomio, sottocampo degli invarianti di un gruppo di
automorfismi di un campo. Cenni sulle estensioni di Galois e sul teorema fondamentale della teoria di Galois.
Testi consigliati
M. CURZIO, P. LONGOBARDI, M. MAJ - Lezioni di algebra , Liguori, 1994 (II ed. 1996).
N. JACOBSON - Basic Algebra I, II, Freeman, San Francisco, 1980.
Modalità di valutazione
Prova scritta e prova orale.
ALGEBRA III
Prof. Giovanni Vincenzi
Obiettivi formativi
Questo corso è dedicato allo studio della teoria di Galois sulla risoluzione per radicali delle equazioni algebriche su di
un campo.
Contenuti del corso
Richiami di teoria dei campi. Gruppi di automorfismi di un campo. Richiami sui gruppi risolubili. Estensioni normali ed
estensioni separabili di un campo.
Grado di separabilità di un’estensione. Estensioni di Galois: estensioni binomie; estensioni ciclotomiche. Equazioni
risolubili per radicali: teorema di Galois, teorema di Artin-Schreier. Teorema di Ruffini-Abel. Norma e traccia di
un’estensione di Galois. Estensioni cicliche: il teorema 90 di Hilbert. Approfondimenti: teoria di Jacobson Bourbaki,
teoria dei corpi.
Testi consigliati
Appunti distribuiti durante il corso.
Modalità di valutazione
Prova orale.
ALGEBRA IV
Prof.ssa Mercede Maj
Obiettivi formativi
Scopo di questo corso è di approfondire lo studio della teoria dei moduli su di un anello unitario. Vengono inoltre
illustrati risultati di teoria dei numeri cardinali e ordinali e di teoria delle categorie.
Contenuti del corso
Numeri cardinali e ordinali.
Categorie e funtori.
Teoria dei moduli: esempi, somme e prodotti diretti di una famiglia di moduli, moduli semplici, moduli fedeli, moduli
periodici e aperiodici.
Moduli liberi, moduli proiettivi , iniettivi, divisibili.
Moduli su di un anello principale.
Prodotto tensoriale.
Testi consigliati
M. CURZIO, P. LONGOBARDI, M. MAJ - Lezioni dai Algebra - Liguori Editore, Napoli, 1994.
T.W. HUNGERFORT - Algebra - Springer-Verlag, Berlin, 1974.
T.S. BLYTH - Module Theory - Clarendon Press, Oxford, 1990.
Modalità di valutazione
Prova orale.
ANALISI FUNZIONALE I
Prof.ssa Luciana Sgambati
Obiettivi formativi
Scopo del corso è lo studio dei problemi istituzionali dell’Analisi Funzionale.
Contenuti del corso
Teoremi fondamentali di analisi lineare (Hahn-Banach, applicazione aperta, uniforme limitatezza, grafico chiuso).
Topologie deboli e spazi convessi.
Testi consigliati
H. BREZIS, Analisi Funzionale, Liguori Editore.
Modalità di valutazione
Prova orale.
ANALISI MATEMATICA I
Prof.ssa Maria Transirico
Obiettivi formativi
Il corso di Analisi Matematica I è dedicato essenzialmente allo studio delle funzioni reali di una variabile reale e alla
teoria dei limiti di tali funzioni.
Gli obiettivi formativi del corso consistono nell’acquisizione dei risultati e delle tecniche dimostrative, nonché nella
capacità di utilizzare i relativi strumenti di calcolo.
Contenuti del corso
1. Strutture algebriche: prime definizioni ed esempi.
2. I numeri reali.
3. Le funzioni reali.
4. I numeri complessi.
5. Limiti di successioni.
6. Limiti di funzioni e funzioni continue.
7. Complementi ai limiti.
Testi consigliati
P. MARCELLINI, C. SBORDONE - Analisi Matematica uno - Liguori Editore.
P. MARCELLINI, C. SBORDONE - Esercitazioni di Matematica I - Liguori Editore.
A. ALVINO, L. CARBONE, G. TROMBETTI - Esercitazioni di Matematica I - Liguori Editore.
M. TROISI - Analisi Matematica I - Liguori Editore.
D. GRECO, G. STAMPACCHIA - Esercitazioni di Matematica Volume primo - Liguori Editore.
Modalità di valutazione
Prova scritta e prova orale.
ANALISI MATEMATICA II
Prof.ssa Maria Transirico
Obiettivi formativi
Il corso di Analisi Matematica II è dedicato essenzialmente alla teoria della derivazione e dell’integrazione per funzioni
reali di una variabile reale, e allo studio delle serie numeriche.
Gli obiettivi formativi del corso consistono nell’acquisizione dei risultati e delle tecniche dimostrative, nonché nella
capacità di utilizzare gli strumenti del calcolo differenziale e del calcolo integrale.
Contenuti del corso
1. Derivate.
2. Applicazioni delle derivate. Studio di funzioni.
3. Integrazione secondo Riemann.
4. Integrali indefiniti.
5. Formula di Taylor.
6. Serie numeriche.
Testi consigliati
P. MARCELLINI, C. SBORDONE - Analisi Matematica uno - Liguori Editore.
P. MARCELLINI, C. SBORDONE - Esercitazioni di Matematica I - Liguori Editore.
A. ALVINO, L. CARBONE, G. TROMBETTI - Esercitazioni di Matematica I - Liguori Editore.
M. TROISI - Analisi Matematica I - Liguori Editore.
D. GRECO, G. STAMPACCHIA - Esercitazioni di Matematica Volume primo - Liguori Editore.
Modalità di valutazione
Prova scritta e prova orale
ANALISI MATEMATICA III
Prof.ssa Luciana Sgambati
Obiettivi formativi
Il corso di Analisi Matematica III è dedicato allo studio delle successioni e serie di funzioni, alla teoria delle funzioni di
più variabili reali ed allo studio delle equazioni differenziali. Relativamente a tali argomenti vengono forniti i risultati
fondamentali, le tecniche di dimostrazione e gli strumenti di calcolo. Sono richieste solide basi della teoria delle
funzioni numeriche di una variabile reale, che è oggetto dei corsi di Analisi Matematica I e Analisi Matematica II; si
ritiene altresì indispensabile un’adeguata conoscenza dei risultati e delle tecniche di calcolo tipiche dell’algebra lineare.
Contenuti del corso
1. Successioni e serie di funzioni.
2. Funzioni di più variabili reali.
3. Equazioni differenziali ordinarie.
4. Equazioni differenziali lineari.
Testi consigliati
N. FUSCO, P. MARCELLINI, C. SBORDONE - Analisi Matematica due - Liguori Editore.
P. MARCELLINI, C. SBORDONE - Esercitazioni di Matematica II - Liguori Editore.
Modalità di valutazione
Prova scritta e prova orale.
ANALISI MATEMATICA IV
Prof.ssa Luciana Sgambati
Obiettivi formativi
Il corso di Analisi Matematica IV è dedicato alla teoria degli integrali curvilinei, delle forme differenziali, degli
integrali multipli e delle funzioni implicite. Relativamente a tali argomenti vengono forniti i risultati fondamentali, le
tecniche di dimostrazione e gli strumenti di calcolo. Sono richieste solide basi della teoria delle funzioni numeriche di
una variabile reale, che è oggetto dei corsi di Analisi Matematica I e Analisi Matematica II, e degli argomenti trattati nel
corso di Analisi Matematica III. Si ritiene altresì indispensabile un’adeguata conoscenza dei risultati e delle tecniche di
calcolo tipiche dell’algebra lineare.
Contenuti del corso
1. Curve ed integrali curvilinei.
2. Forme differenziali lineari.
3. Integrali multipli.
4. Cenni su superfici ed integrali superficiali.
5. Funzioni implicite.
Testi consigliati
N. FUSCO, P. MARCELLINI, C. SBORDONE - Analisi Matematica due - Liguori Editore.
P. MARCELLINI, C. SBORDONE - Esercitazioni di Matematica II - Liguori Editore.
Modalità di valutazione
Prova scritta e prova orale
ANALISI MATEMATICA V
Prof. Antonio Vitolo
Obiettivi formativi
Ampliamento delle conoscenze matematiche di base: fondamenti della teoria delle funzioni di variabile complessa,
relative tecniche di calcolo e introduzione ad alcuni settori di applicazione.
Contenuti del corso
1. Rappresentazioni del piano complesso.
2. Funzioni olomorfe e teorema integrale di Cauchy.
3. Formula integrale di Cauchy e applicazioni.
4. Serie di funzioni in campo complesso.
5. Serie di Taylor e zeri delle funzioni olomorfe.
6. Serie di Laurent e classificazione delle singolarità isolate.
7. Teoria dei residui e principio dell’argomento.
8. Funzioni speciali: funzione Gamma di Eulero e funzioni di Bessel.
9. Serie di Dirichlet e funzione Zeta di Riemann.
Testi consigliati
D. GRECO, Complementi di Analisi Matematica, Liguori (NA).
J.B. CONWAY, Complex Analysis, Springer-Verlag.
Modalità di valutazione
Prova scritta e discussione orale.
ANALISI MATEMATICA VI
Prof. Antonio Vitolo
Obiettivi formativi
Ampliamento delle conoscenze matematiche di base e introduzione all’uso di metodi matematici di livello superiore:
teoria della misura e dell’integrazione di Lebesgue, nonché spazi di funzioni sommabili; spazi di Banach e di Hilbert;
analisi di Fourier.
Contenuti del corso
1. Spazi di Banach di funzioni limitate e di funzioni continue.
2. Teoria della misura.
2. Integrazione in spazi di misura.
P
4. Spazi L : disuguaglianza di Hölder, completezza, approssimazione con funzioni regolari.
5. Spazi di Hilbert: decomposizione ortogonale, rappresentazione delle forme lineari, sistemi
ortonormali, modelli ed esempi in dimensione infinita.
6. Funzioni periodiche e integrale di Riemann.
7. Serie di Fourier: convergenza puntuale, uniforme, integrazione termine a termine.
1
8. Trasformata di Fourier in L : proprietà formali ed effetto regolarizzante.
9. Formula di inversione della trasformata di Fourier e applicazione alle equazioni differenziali.
2
10. Trasformata di Fourier in L e teorema di Plancherel.
Testi consigliati
G. GIUSTI, Analisi Matematica II, Boringhieri (FI).
H. BREZIS, Analisi Funzionale, Liguori (NA).
A. TESEI, Istituzioni di Analisi Superiore, Boringhieri (FI).
W. RUDIN, Analisi reale e complessa, Boringhieri (FI).
Modalità di valutazione
Prova scritta e discussione orale.
CALCOLO DELLE PROBABILITA’ E STATISTICA
Prof. Antonio Di Crescenzo
Obiettivi formativi
Conoscenze di livello medio di teoria della probabilità. Essere in grado di risolvere problemi che richiedono l’utilizzo
degli strumenti di tale teoria.
Contenuti del corso
Probabilità
Spazio di probabilità. Probabilità condizionata. Indipendenza. Primi teoremi della probabilità.
Variabili aleatorie
Variabili aleatorie. Funzioni di ripartizione e relative proprietà. Variabili aleatorie discrete ed assolutamente continue.
Valore atteso, varianza, momenti. Principali distribuzioni di probabilità. Vettori aleatori. Funzioni di ripartizione
multiple. Indipendenza. Covarianza e correlazione.
Teorema centrale di convergenza
Funzione generatrice dei momenti. Funzione caratteristica. Disuguaglianza di Chebyshev. Criteri di convergenza per
successioni di variabili aleatorie. Legge dei grandi numeri. Teorema centrale di convergenza.
Processi stocastici
Generalità. Processi di Marcov. Processo di Poisson. Catene di Markov. Processo di moto Browniano. Applicazioni.
Testi consigliati
DALL'AGLIO G. (2000) Calcolo delle Probabilità. II edizione. Zanichelli.
ROSS G. (1996) Stochastic Processes. II edizione. John Wiley & Sons.
Modalità di valutazione
Prova orale.
CALCOLO NUMERICO
Prof.ssa Beatrice Paternoster
Obiettivi formativi
Il corso è finalizzato alla trattazione dei principali problemi che si incontrano nello sviluppo di software matematico
efficiente. E' quindi dedicato alla conoscenza teorica ed all'analisi critica dei principali metodi numerici relativi ad
argomenti di base, alle metodologie di progettazione di algoritmi efficienti e all'uso di opportuni ambienti di calcolo
numerico per la risoluzione di problemi di calcolo scientifico.
Particolare importanza rivestono le Esercitazioni in Laboratorio, rivolte a sperimentare i suddetti metodi, stimare
l'attendibilità dei risultati ottenuti, sviluppare elementi di software matematico e valutarne le prestazioni.
Contenuti del corso
Richiami di analisi degli errori ed aritmetica floating – point.
Approssimazione di dati e funzioni. Interpolazione polinomiale e con funzioni spline. Approssimazione nel senso dei
minimi quadrati.
Metodi iterativi per la risoluzione di equazioni non lineari.
Integrazione numerica: Formule di Newton - Cotes e di Gauss. Integratori automatici basati su schemi fissi e adattativi.
Autovalori di matrici. Metodi iterativi e metodi basati su trasformazioni di similitudine.
Linguaggio di programmazione Matlab.
Sviluppo di codici relativi ai principali algoritmi trattati.
Testi consigliati
J.F.Epperson – Introduzione all’analisi numerica: teoria, metodi, algoritmi – McGraw-Hill.
G. Monegato - Fondamenti di Calcolo Numerico - Ed. CLUT.
Modalità di valutazione
Per studenti che svolgono con profitto il corso: una prova intercorso sullo sviluppo di elementi di software matematico,
esame finale.
Per studenti che non hanno svolto con profitto il corso o che non hanno preso parte al corso: attività di tutorato in
laboratorio.
CALCOLO NUMERICO II
Prof.ssa Elvira Russo
Obiettivi formativi
Il corso è finalizzato a mettere lo studente in grado di acquisire competenze per la risoluzione numerica di problemi
modellizzati da equazioni differenziali ordinarie, nonché per sviluppare software matematico di qualità.
Contenuti del corso
METODI NUMERICI PER EQUAZIONI DIFFERENZIALI ORDINARIE.
Metodi di approssimazione di tipo analitico. Metodi lineari multistep. Metodi predictor-corrector. Metodi BDF. Metodi
non-lineari ad un passo. Metodi di Runge-Kutta. Ordine. Stime degli errori. Consistenza. Convergenza. Zero-stabilità.
Teoria della debole stabilità. Sistemi stiff. Struttura di un algoritmo a passo variabile. Procedure di starting. Stima
dell’errore di troncamento. Strategie per il cambiamento del passo. Valutazione del software.
Testi consigliati
E.Hairer, S.P.Norsett, G.Wanner - Solving Ordinary Differential Equations - I.S.C.M. Springer Verlag.
J.B.Lambert - Computational methods in Ordinary Differential Equations - J.Wiley Sons.
Metodi di valutazione
Per studenti che svolgono con profitto il corso: test di verifica, prova di laboratorio, progetto, colloquio finale.
Per studenti che non hanno svolto con profitto il corso o che non hanno preso parte al corso: progetto e colloquio finale.
EQUAZIONI DIFFERENZIALI
Prof.ssa Anna Canale
Obiettivi formativi
Il corso tratta vari aspetti legati allo studio delle equazioni differenziali. Lo scopo è quello di ottenere che lo studente
abbia un buon livello di chiarezza e conoscenza delle tematiche trattate e sviluppi una capacità di sintesi che lo aiuti ad
affrontare le problematiche che incontra nel corso dei suoi studi.
Contenuti del corso
Teoria delle equazioni differenziali. Equazioni lineari. Problemi ai limiti. Analisi qualitativa delle soluzioni. Equazioni
esatte. Metodi risolutivi di equazioni differenziali. Sistemi di equazioni differenziali.
Testi consigliati
N. Fusco - P. Marcellini - C. Sbordone, Analisi Matematica II, Liguori Editore.
E. Giusti, Analisi Matematica 2, Boringhieri Editore.
F. Conti, Calcolo, McGraw-Hill Libri Italia.
F. Conti - P. Aquistapace - A.Savoini, Analisi Matematica. Teoria e Applicazioni, McGraw-Hill Libri Italia.
P. Marcellini - C. Sbordone, Esercitazioni di Analisi Matematica, Volume II, parte prima, Liguori Editore.
Modalità di valutazione
Preparazione di una tesina ed esame orale.
FISICA GENERALE I
Prof. Mario Fusco Girard
Obiettivi formativi
Formazione di base nel campo della fisica classica: meccanica e termodinamica.
Contenuti del corso
Grandezze fisiche e loro misura. Sistemi di unità. Algebra dei vettori. Moto in una dimensione: velocità ed
accelerazione scalari. Moto nel piano e nello spazio. Forze. I principi della dinamica. Energia cinetica. Lavoro. Forze
conservative. Conservazione dell’energia meccanica. Sistemi di punti materiali. Gravitazione. Oscillazioni.
Temperatura e calore. Primo principio della termodinamica. Secondo principio della termodinamica. Concetto di
entropia.
Testi consigliati
D. Halliday - R. Resnick, Fisica, vol. I.
Modalità di valutazione
Esame finale.
FISICA GENERALE II
Prof. Mario Fusco Girard
Obiettivi formativi
Formazione di base nel campo della fisica classica: elettromagnetismo ed ottica.
Contenuti del corso
Carica elettrica e fenomeni elettrostatici elementari. Campo elettrico e sue proprietà. Conduttori ed isolanti, capacità.
Correnti elettriche continue, leggi di Ohm, potenza elettrica ed effetto Joule, circuiti elementari. Campo magnetico e
correnti elettriche. Forze magnetiche su correnti. Induzione elettromagnetica. Circuiti RL ed RLC. Correnti alternate.
Equazioni di Maxwell. Onde elettromagnetiche. Ottica. Relatività ristretta. Cenni di fisica moderna.
Testi consigliati
D. Halliday - R. Resnick, Fisica, vol. II.
Modalità di valutazione
Esame finale.
FISICA MATEMATICA I
Prof. Ettore Laserra
Obiettivi formativi
Fornire una buona conoscenza dei fondamenti e dei metodi della Fisica Matematica, in particolare della Meccanica.
Contenuti del corso
RICHIAMI DI TEORIA DEI VETTORI.
SISTEMI DI VETTORI APPLICATI.
CENNI DI CALCOLO TENSORIALE.
SISTEMI DINAMICI: Richiami sugli spazi affini. Sistemi dinamici e curve integrali. L’equazione di Weierstrass. Integrali primi. Stabilità dei
punti critici.
CINEMATICA: Cinematica del punto. Rappresentazione in coordinate generiche. Rappresentazione intrinseca. Moti centrali. Moti su di una
superficie. Moti geodetici. Rotazioni. Cinematica del corpo rigido. Cambiamenti di riferimento. Moti rigidi particolari. Moti rigidi composti.
MOTI RELATIVI.
GEOMETRIA DELLE MASSE: Baricentro di un sistema materiale discreto e continuo. Momenti d’inerzia di un sistema materiale discreto e
continuo. Tensore d’inerzia.
LA MECCANICA DI NEWTON ED EULER: Dinamica del punto libero. Grandezze cinetiche fondamentali. Dinamica del punto vincolato.
Esempi notevoli. Dinamica dei sistemi finiti di punti materiali. Dinamica del corpo rigido. Corpo rigido con un punto fisso. Corpo rigido con un
asse fisso.
Testi consigliati
S. BENENTI, Modelli matematici della Meccanica, vol. I, Celid.
G. CARICATO - Fondamenti di Meccanica Newtoniana - Cisu, Roma.
M. FABRIZIO - Elementi di Meccanica Classica, Zanichelli, Bologna, 2002.
F. STOPPELLI - Appunti di Meccanica Razionale – Liguori, Napoli.
Modalità di valutazione
Per studenti che svolgono con profitto il corso: prova intercorso.
FISICA MATEMATICA II
Prof. Ettore Laserra
Obiettivi formativi
Fornire una buona conoscenza dei fondamenti e dei metodi della Fisica Matematica, in particolare della Meccanica
Analitica e del Calcolo delle Variazioni.
Contenuti del corso
ELEMENTI DI CALCOLO DELLE VARIAZIONI.
LA MECCANICA DI LAGRANGE (MECCANICA ANALITICA): Varietà differenziabili. Fibrati tangenti. Campi
vettoriali. Forme differenziali. Sistemi olonomi. Le equazioni di Lagrange. Meccanica riemanniana. Sistemi
lagrangiani. Integrali primi. Il principio dell’azione stazionaria.
LA MECCANICA DI HAMILTON (MECCANICA SIMPLETTICA): Fibrati cotangenti e sistemi hamiltoniani. La
trasformazione di Legendre. Il metodo di Jacobi. Parentesi di Poisson e integrali primi. Sottovarietà lagrangiane. Varietà
simplettiche e sistemi hamiltoniani integrabili.
Testi consigliati
S. BENENTI, Modelli matematici della Meccanica, vol. I, Celid.
V.I. SMIRNOV, Corso di Matematica Superiore, vol. 4, tomo 1, Mir.
Modalità di valutazione
Per studenti che svolgono con profitto il corso: prova intercorso.
FONDAMENTI DI GEOMETRIA
Prof. Francesco Bottacin
Obiettivi formativi
L’obiettivo del corso è quello di descrivere a grandi linee lo sviluppo storico della geometria, da Euclide fino ai giorni
nostri, soffermandosi sulle idee principali che, in varie epoche, hanno rivoluzionato lo studio della geometria.
Contenuti del corso
Gli ''Elementi'' di Euclide. Analisi della struttura dell'opera, con particolare riferimento al Libro I.
Il problema dell'indipendenza e della non contraddizione degli assiomi.
''I Principi Fondamentali della Geometria'' di Hilbert. Analisi della struttura dell'opera, con particolare riferimento al
Capitolo 1. Il problema dell'indipendenza e della non contraddizione degli assiomi, e la soluzione proposta da Hilbert. Il
fallimento del programma di Hilbert. I teoremi di incompletezza di Gödel (brevi cenni di Logica Matematica).
Introduzione alle geometrie non euclidee. La geometria ellittica di Riemann. La geometria iperbolica di Lobachevski. I
tre modelli del piano iperbolico: il modello di Klein, il modello del disco unitario
di Poincaré e il modello del semipiano superiore. Studio della geometria iperbolica nel modello del semipiano
superiore. Le rette nel piano iperbolico. Le isometrie del piano iperbolico. I triangoli nel piano iperbolico. Criteri per la
congruenza dei triangoli. L'area di un triangolo. La somma degli angoli interni di un triangolo. Il modello del disco
unitario di Poincaré. La metrica iperbolica nel modello del disco unitario.
I cerchi nel piano iperbolico (nei modelli del disco unitario e del semipiano superiore). La lunghezza della circonferenza
e l'area di un cerchio di raggio R. Cicli, orocicli e ipercicli.
Una breve introduzione alle idee e ai metodi che stanno alla base della geometria algebrica moderna.
Spazi affini e varietà affini su un corpo K. Ideale associato a una varietà affine e anello delle funzioni regolari. Ideali
radicali e ideali primi. Dimensione di una varietà affine e dimensione di Krull di un anello.
Morfismi di varietà e omomorfismi di anelli. Schemi affini: lo spettro di un anello commutativo con unità.
Testi consigliati
Gli Elementi di Euclide.
I Principi Fondamentali della Geometria di Hilbert.
E.E. Moise, ''Elementary Geometry from an Advanced Standpoint'', Addison-Wesley, Reading MA, 1974.
E. Agazzi, ''Le Geometrie Non Euclidee''.
A. Ramsay, ''Introduction to Hyperbolic Geometry''.
G.E. Martin, ''The Foundations of Geometry''.
R. Bonola, ''Non-Euclidean Geometry''.
M.J. Greenberg, ''Euclidean and Non-Euclidean Geometries'', Freeman & Company, New York, 1974.
Modalità di valutazione
Esame orale e/o preparazione di una lezione su un argomento non trattato durante il corso.
FONDAMENTI DI INFORMATICA E LABORATORIO
Prof. Domenico Parente
Obiettivi formativi
L'insegnamento si propone di fornire allo studente le capacità di realizzare un semplice programma in linguaggio C per
computer che risolva problemi scientifici elementari.
Contenuti del corso
Linguaggio C: Programmazione di base, strutture di controllo e file di dati. Programmazione modulare, array, gestione
dati di tipo carattere. Introduzione alla soluzione di problemi applicati. Struttura di un programma C. Costanti e
variabili. Istruzioni di assegnamento. Operazioni di input e output. Funzioni matematiche. Sviluppo di algoritmi.
Espressioni condizionali. Istruzioni di selezione.Cicli. File di dati. Programmi modulari. Definizione di funzioni.
Definizione ed utilizzo di array. Array come parametri di funzione. Tipo di dati carattere. Inizializzazione e calcolo con
dati di tipo carattere. Funzioni di gestione dei dati di tipo carattere.
Testi consigliati
Delores M. Etter, “Introduzione al Linguaggio C”, Apogeo.
Compilatore C, “DevCpp”, rilasciato gratuitamente con licenza GNU GPL e scaricabile alla seguente URL:
sourceforge.net/projects/dev-cpp/.
Codice di esercizi svolti in linguaggio C, consultabili dal sito web del docente.
Modalità di valutazione
Per il superamento dell'esame e' necessario superare una prova scritta in cui si chiede di scrivere un breve programma in
linguaggio C per la risoluzione di un semplice problema e quindi sostenere un colloquio orale.
GEOMETRIA I
Prof. Giovanni Sparano
Obiettivi formativi
Il corso di Geometria I intende fornire i primi strumenti di algebra lineare necessari allo studio della geometria affine ed
euclidea.
Contenuti del corso
1. Matrici e determinanti.
2. Sistemi di equazioni lineari.
3. Spazi vettoriali.
4. Applicazioni lineari.
5. Spazi vettoriali euclidei.
Testi consigliati
S. ABEASIS, Elementi di algebra lineare e geometria, Zanichelli.
R. ESPOSITO, A. RUSSO, Lezioni di geometria parte prima, Liguori.
S. LANG, Algebra lineare, Bollati Boringhieri.
E. SERNESI, Geometria 1, Bollati Boringhieri.
S. LIPSCHUTZ Algebra lineare McGraw-Hill.
Modalità di valutazione
Prova scritta e prova orale.
GEOMETRIA II
Prof. Giovanni Sparano
Obiettivi formativi
L’obiettivo del corso di Geometria II è fornire alcuni strumenti di algebra lineare e un’introduzione alla geometria
affine ed euclidea.
Contenuti del corso
1. Spazi vettoriali euclidei.
2. Diagonalizzazione degli endomorfismi.
3. Spazi affini ed euclidei.
Testi consigliati
R. ESPOSITO, A. RUSSO, Lezioni di geometria parte prima, Liguori.
S. LANG, Algebra lineare, Bollati Boringhieri.
E. SERNESI, Geometria 1, Bollati Boringhieri.
S. LIPSCHUTZ, Algebra lineare McGraw-Hill.
Modalità di valutazione
Prova scritta e prova orale.
GEOMETRIA III
Prof.ssa Anna Di Concilio
Obiettivi formativi
Lo scopo del corso di Geometria III consiste nell’ approfondire la conoscenza della geometria euclidea. e
nell’introdurre e studiare esempi di geometrie non euclidee. Inoltre, nel mostrare l’uso del metodo di generalizzazione,
che è una strategia tipica della matematica, per introdurre gli spazi topologici come naturale generalizzazione degli
spazi metrici e questi a loro volta come naturale generalizzazione degli spazi euclidei.
Contenuti del corso
Che cos’è una geometria? Le geometrie nel senso del Programma di Erlangen di F. Klein. La geometria affine, delle
similitudini e metrica degli spazi euclidei. Esempi di geometrie iperboliche. La geometria proiettiva degli spazi
proiettivi reali. Classificazione proiettiva, affine e metrica delle coniche reali. Un esempio di generalizzazione: dagli
spazi euclidei agli spazi metrici, dagli spazi metrici agli spazi topologici.
Testi consigliati
M .Eisenberg, Topology, Holt- Rinehart-Winston N.Y.
R. Engelking, General Topology, PWN Polish scientific Publishers.
E. Sernesi, Geometria I, Bollati Boringhieri.
G. Tallini, Strutture Geometriche, Liguori Editore.
S. Willard, General Topology, Addison-Wesley publishing Company.
Modalità di valutazione
Prova orale.
GEOMETRIA IV
Prof. Alexandre Vinogradov
Obiettivi formativi
Obiettivo principale del corso è introdurre lo studente ai concetti di base e ai metodi della geometria differenziale su
materiale più semplice possibile, e sviluppare le capacità di interpretazione geometrica di materiale algebrico e analitico
e viceversa.
Contenuti del corso
Il corso è suddiviso in tre parti. La prima, introduttiva, contiene il necessario materiale preliminare: una sintesi di
geometria affine e di topologia naturale degli spazi euclidei, l’interpretazione geometrica di alcuni elementi del calcolo
differenziale di funzioni di più variabili. La seconda parte è un percorso che parte dallo studio generale delle
sottovarietà negli spazi affini e finisce con l’introduzione delle varietà astratte. La terza parte è dedicata alla teoria
metrica delle curve negli spazi euclidei multi-dimensionali. Include la teoria degli spazi oscuratori di una curva, n-edro
mobile di Fernet, curvature superiori di una curva e metodi del loro calcolo. I punti centrali qui sono due teoremi
fondamentali: il primo, sulla forma di una curva e il secondo sulla realizzazione delle curvature assegnate a priori.
Testi consigliati
Appunti del corso.
Modalità di valutazione
Colloquio preliminare ed esame orale.
GEOMETRIA V
Prof. Alexandre Vinogradov
Obiettivi formativi
Obiettivo principale del corso è introdurre lo studente ai concetti di base e ai metodi della geometria differenziale su
materiale più semplice possibile, e sviluppare le capacità di interpretazione geometrica di materiale algebrico e analitico
e viceversa.
Contenuti del corso
Il corso è la continuazione naturale di Geometria IV ed è dedicato principalmente alla geometria metrica delle
sottovarietà di spazi Euclidei. Attenzione speciale si dà alla distinzione fra la geometria esterna di una sottovarietà e
quella interna. Quest’ultima fornisce un percorso naturale per introdurre l’idea della geometria Riemanniana astratta alla
fine del corso. Elementi di base della geometria metrica si sviluppano per le sottovarietà generali mentre i risultati più
concreti che richiedono alcune tecniche più delicate si dimostrano solo per le superfici. In particolare, si discutono le
equazioni di Gauss-Wiengarten, il “teorema egregio” di Gauss, proprietà estreme delle curve geodetiche, la
classificazione delle superfici di curvatura di Gauss costante ed il problema del “quinto postulato”.
Testi consigliati
Appunti del corso.
Modalità di valutazione
Colloquio preliminare ed esame orale.
GEOMETRIA VI
Prof.ssa Anna Di Concilio
Obiettivi formativi
Lo scopo del corso di Geometria VI consiste nell’ introdurre allo studio della topologia algebrica e nel dare un
esempio di classificazione: il teorema di classificazione topologica delle superfici connesse e compatte con e senza
bordo.
Contenuti del corso
Omotopia tra funzioni e tra spazi. Retratti e retratti per deformazione. Connessione semplice. Omotopia di cammini. Il
gruppo fondamentale. Calcolo del gruppo fondamentale della circonferenza. Metodi di calcolo del gruppo
fondamentale. Applicazioni: il teorema fondamentale dell’algebra, il teorema del punto fisso in dimensione due.
Superfici. Superfici con bordo. Somma connessa di superfici. Forma canonica di una somma connessa di tori e di piani
proiettivi reali. Sfere con manici. Triangolazioni. Caratteristica di Eulero-Poincaré. Orientabilità e non. Classificazione
topologica delle superfici connesse e compatte con o senza bordo.
Testi consigliati
R. Engelking, General Topology, PWN Polish scientific Publishers 1998.
C. Godbillon, Elements of Topologie Algebrique, Collection Methodes Hermann Paris 1971.
W.S. Massey, Algebraic Topolog : An Introduction, Springer-Verlag 1991.
S. Willard, General Topology, Addison-Wesley publishing Company 1970.
Modalità di valutazione
Prova orale.
LABORATORIO DI FISICA GENERALE I
Prof. Carmine Attanasio
Obiettivi formativi
Conoscenza del metodo scientifico. Capacità di effettuare semplici esperimenti di meccanica e termodinamica.
Trattamento dei dati sperimentali.
Contenuti del corso
Grandezze fisiche fondamentali e derivate. Errori di misura. Trattazione e tabulazione dei dati sperimentali. Grafici dei
dati sperimentali. Cenni al metodo dei minimi quadrati. Misura della densità di un solido. Misura della costante elastica
di una molla. Verifica del II principio della dinamica. Misura dell’accelerazione di gravità. Misura del calore specifico
di un solido. Misura della costante di tempo di un termometro..
Testi consigliati
M. Severi, Introduzione alla esperimentazione fisica, Zanichelli.
G. Cannelli, Metodologie sperimentali in Fisica, Edises.
Modalità di valutazione
Discussione orale e delle relazioni delle attività di laboratorio.
LABORATORIO DI FISICA GENERALE II
Dott. Gaetano Lambiase
Obiettivi formativi
Approfondimento della formazione di base nel campo della fisica classica: elettromagnetismo ed ottica.
Contenuti del corso
Esercitazioni di elettromagnetismo e di ottica.
Testi consigliati
D. Halliday - R. Resnick, Fisica, vol. II.
Modalità di valutazione
Esame finale.
LABORATORIO DI MATEMATICA COMPUTAZIONALE
Dott.ssa Dajana Conte
Obiettivi formativi
Scopo del corso è mostrare allo studente la possibilità di utilizzare un ambiente di calcolo scientifico per visualizzare,
fare ipotesi, prevedere andamenti, trovare risultati inerenti argomenti già trattati nei corsi di base del primo anno. Il
corso è organizzato in unità didattiche indipendenti.
Contenuti del corso
Significati geometrici: uso delle primitive del Mathematica per analizzare approssimazioni locali e globali, per
visualizzare l’approssimazione dei minimi quadrati, per scoprire interessanti proprietà della funzione esponenziale.
Calcoli numerici: scoprire l’andamento di successioni e serie. Prove numeriche e visualizzazioni con il Matematica.
Calcolo simbolico: avanzare ipotesi e dimostrare teoremi con l’uso delle primitive simboliche del Mathematica. Un
caso particolare: l’ordine di infinito del fattoriale.
Il sistema Mathematica: linguaggio, ambiente di lavoro, i notebooks, grafici, la libreria matematica, i packages standard,
il calcolo numerico e simbolico.
Testi consigliati
The Matematica Book (on line).
Modalità di valutazione
Per studenti che svolgono con profitto il corso
1 progetto da consegnare al termine del corso
difesa del progetto
Per studenti che non hanno svolto con profitto il corso o che non hanno preso parte al corso
Sviluppo di un mini progetto in aula con il matematica
LABORATORIO DI PROGRAMMAZIONE E CALCOLO
Dott. Giovanni Capobianco
Obiettivi formativi
Lo scopo del corso è fornire allo studente un’introduzione ai metodi numerici, alla scelta e alla costruzione di algoritmi
per la matematica numerica e all’uso del linguaggio C e di ambienti per il calcolo scientifico.
Contenuti del corso
Risoluzione di un problema con il calcolatore: dal problema reale al metodo, all’algoritmo, alla codifica, all’analisi dei
risultati.
Sorgenti e propagazione degli errori. Problema ben posto, ben condizionato. Stabilità di un algoritmo. Rappresentazione
floating point.
Risoluzione di sistemi lineari; metodi diretti e iterativi; Metodo di eliminazione di Gauss; Pivoting. Fattorizzazione LU;
metodo di Choleski; Costruzione e valutazione di algoritmi e codici.
Metodi iterativi per Sistemi Lineari: Metodi di Jacobi, Gauss-Seidel e SOR; Convergenza. Costruzione e valutazione di
algoritmi e codici.
Interpolazione polinomiale; Polinomio interpolante di Lagrange. Errore. Il polinomio di Newton; Errore; Convergenza.
Funzioni polinomiali a tratti; Spline; Spline cubica interpolante. Approssimazione nel senso dei minimi quadrati: caso
discreto. Costruzione e valutazione di algoritmi e codici.
Il linguaggio C: hedaer files, operatori aritmetici, variabili e le costanti, l’input e l’output; assegnazione, strutture
condizionali, i cicli, gli array, le function.L’ambiente Matlab: conoscenze di base; le funzioni su matrici; i grafici.
Testi consigliati
J.F.Epperson, Introduzione all'analisi numerica - Ed. Mc-Graw-Hill.
V. Cominciali, Analisi Numerica - Ed. Mc Graw Hill.
G. Monetato, Fondamenti di Calcolo Numerico - Ed. Cluet.
Modalità di valutazione
Per studenti che svolgono con profitto il corso
1) 2 progetti da consegnare durante il corso
2) difesa dei progetti e verifica orale su altri argomenti del corso
Per studenti che non hanno svolto con profitto il corso o che non hanno preso parte al corso
1) test di costruzione di un algoritmo a partire da un metodo e codifica in C dell’algoritmo
2) verifica orale sugli argomenti del corso
LINGUAGGI DI PROGRAMMAZIONE
Prof.ssa Margherita Napoli
Obiettivi formativi
L'insegnamento si propone di fornire allo studente elementi sui modelli dei dati e gli algoritmi e l’acquisizione della
conoscenza di tecniche fondamentali di programmazione.
Contenuti del corso
1) Metodologie di programmazione. Tipi di dati astratti e modelli dati. Programmazione iterativa: cicli iterativi e
algoritmi iterativi. Invarianti di cicli. Induzione. Programmazione ricorsiva: Definizioni ricorsive, funzioni ricorsive e
prove induttive.
2) Analisi delle prestazioni di un programma:complessità temporale, passi di programma, la complessità in pratica,
notazione asintotica. Relazioni di ricorrenza e loro risoluzione. Ogni argomento nelle parti 1) e 2) è espletato anche
mediante l'applicazione a problemi esplicativi paradigmatici.
3) Il Modello dati Lista. Implementazioni di liste. Liste ordinate. Stacks e code: modelli astratti e loro implementazioni.
Realizzazione di chiamate di procedura mediante stack,
4) Il Modello dati Albero. Alberi e loro rappresentazioni. Il modello dati albero binario. Rappresentazione di alberi
binari. Attraversamento di alberi.
Testi consigliati
Aho, Ullman: Foundations of Computer Science, C Edition.
Modalità di valutazione
Gli studenti che svolgono con profitto il corso superando test di verifica e prove intercorso, devono svolgere una prova
orale.
Per studenti che non hanno svolto con profitto il corso o che non hanno preso parte al corso è prevista una prova scritta
ed una prova orale.
LOGICA MATEMATICA I
Prof. Antonio Di Nola
Obiettivi formativi
Scopo di questo corso è di affrontare lo studio della logica mediante i sistemi formali.
Contenuti del corso
Algebre di Boole: Insiemi parzialmente ordinati. Reticoli. Reticoli complementati. Reticoli distributivi. Algebre di
Boole. Prime proprieta’ delle algebre di Boole. Filtri e ideali nelle algebre di Boole. Proprieta' della intersezione finita.
Ultrafiltri e loro caratterizzazioni.Teorema dell’ultrafiltro. Lemma di Tarski.
Elementi del Calcolo Preposizionale: La sintassi del calcolo preposizionale. Realizzazioni. Soddisfacibilità.
Tautologie. Un sistema di assiomi per il calcolo preposizionale. Regole di inferenza. Dimostrazioni formali. Teoremi
formali. Teorema di finitezza del calcolo preposizionale. Teorema di deduzione del calcolo preposizionale. L’algebra di
Lindenbaum del calcolo preposizionale. Teorema di completezza del calcolo preposizionale. Teorema di compattezza.
Insiemi di formule consistente. Teorema di completezza generalizzato per il calcolo preposizionale.
Elementi del Calcolo dei Predicati: Il linguaggio del calcolo dei predicati. Quantificatori. Interpretazioni delle
formule del calcolo dei predicati. Strutture relazionali. Realizzazioni e modelli di formule del calcolo dei predicati. Un
sistema di assiomi per il calcolo dei predicati. Regole di inferenza. Dimostrazioni formali. Teoremi formali. Teorema di
finitezza del calcolo dei predicati. Teorema di deduzione del calcolo dei predicati. Insiemi di formule consistente. La
consistenza del calcolo dei predicati. L’algebra di Lindenbaum del calcolo dei predicati. Completezza del calcolo dei
predicati.
Testi consigliati
Appunti dal corso.
Modalità di valutazione
Prova orale.
LOGICA MATEMATICA II
Prof. Giangiacomo Gerla
Obiettivi formativi
Pervenire alla astrazione necessaria per la comprensione di aspetti “universali” delle strutture matematiche del primo
ordine (sia relazionali che algebriche). In particolare buona comprensione di quali siano le proprietà che si trasmettono
per sottostrutture, omomorfismi, isomorfismi e quali siano le proprietà che si conservano per le operazioni di quoziente,
prodotto diretto, ultraprodotto. Comprensione della “filosofia” del formalismo in matematica mostrando come sia
possibile costruire modelli di una teoria matematica in modo sintattico (teorema di completezza, costruzione del
modello di Herbrand).
Contenuti del corso
Operatori algebrici e punti uniti. Proprietà conservate dal passaggio a quoziente. Proprietà conservate dagli
omomorfismi e dalle sottostrutture. Teorema di completezza. Modelli di Herbrand. Prodotti diretti, ultraprodotti,
le classi equazionali. Proprietà che si conservano per prodotti diretti ed ultraprodotti. Applicazioni della teoria
degli ultraprodotti. Campi non archimedei. Cenni di programmazione logica (Prolog).
Testi consigliati
Appunti dal corso scaricabili da http://www.dmi.unisa.it/people/gerla/www/
- Mendelson, Introduzione alla logica matematica, Boringhieri.
- S. J. Russell, P. Norving, Intelligenza Artificiale, Ed. Prentice Hall International.
- M. L. Schagrin, W. J. Rapaport, R.R. Dipert, Logica e computer, Ed. McGraw-Hill.
- A. Asperti, A. Ciabattoni, Logica a Informatica, Ed. McGraw-Hill.
Modalità di valutazione
Esame orale usuale. Prove in laboratorio.
MATEMATICHE COMPLEMENTARI I
Prof. Franco Palladino
Obiettivi formativi
Conoscenza:
di fondamenti di matematica;
dei legami tra le principali aree della matematica;
del pensiero matematico dall’antichità ai tempi moderni.
Contenuti:
Approfondimento delle questioni fondamentali di aritmetica, algebra, geometria, trigonometria (anche per gli aspetti
astronomici) con la considerazione di algoritmi caratteristicamente correlati a questi settori.
Testi consigliati
F. Palladino, L. Lombardi, N. Palladino, “Algoritmi elementari del calcolo aritmetico e algebrico. Tradizione e
modernità”, Bologna, Pitagora Editrice.
F. Palladino, S. Sicoli, “Angoli Linee e Stelle. Origine e sviluppo della trigonometria”, Roma, ARACNE.
oltre a ulteriori numerosi testi e software: “Pascal” – “Visual basic” – “Mathematica”.
Modalità di valutazione
Prova orale.
MATEMATICHE COMPLEMENTARI II
Prof. Giangiacomo Gerla
Obiettivi formativi
• Conoscenza dei momenti fondamentali del pensiero matematico ed acquisizione critica delle nozioni base su
cui è costruita la matematica quali quelle di numero, punto, insieme.
• Capacità di percepire la matematica non come un corpo separato e definitivamente consolidato ma come uno
degli elementi fondamentali della cultura delle varie epoche e pertanto soggetto ad evoluzione ed interazione
con altri settori della cultura.
•
Essere soggetto attivo e critico nell’acquisizione della cultura matematica.
Contenuti del corso
Il corso si occupa di "filosofia della matematica" esaminando criticamente le nozioni-base della matematica ed
inquadrandole nel contesto storico di origine. In particolare: La Scuola pitagorica e sua crisi, gli Elementi di Euclide,
idealizzazione degli enti matematici, il Platonismo, Sesto Empirico. Cartesio e la crisi dell'approccio sintetico. Le
geometrie non euclidee. La teoria degli insiemi. L'aritmetizzazione della geometria e dell'analisi. Infinito attuale ed
infinito potenziale, confronto tra infiniti. Crisi della teoria degli insiemi, le antinomie. Il metodo assiomatico, il punto di
vista fondazionale e quello strutturalista.
Testi consigliati
Appunti del corso scaricabili da http://www.dmi.unisa.it/people/gerla/www/
Morris Kline, La matematica nella cultura occidentale, Feltrinelli.
Bottazzini-Freguglia-Rigatelli (1992) Fonti per la storia della matematica, Sansoni.
Eric T. Bell, I grandi Matematici, Sansoni, 1966.
E. Agazzi, D. Palladino, Le geometrie non euclidee, Mondatori.
E. Casari, La filosofia della matematica del '900, Sansoni.
L. Geymonat, Storia del pensiero filosofico e scientifico, Garzanti.
Rudy Rucker, La mente e l'infinito, Muzzio, 1991.
Modalità di valutazione
Prova orale.
MATEMATICA DI BASE
Prof. Giovanni Vincenzi
Obiettivi formativi
Scopo di questo corso è di introdurre lo studente al linguaggio matematico,abituandolo alla formulazione astratta dei
problemi ed al ragionamento rigoroso.
Contenuti del corso
1. Teoria ingenua degli insiemi.
2. Numeri naturali, principio d'induzione.
3. Elementi di Calcolo Combinatorio
Testi consigliati
Dispense distribuite durante il corso.
Modalità di valutazione
Prova scritta e prova orale.
MATEMATICHE ELEMENTARI DA UN PUNTO DI VISTA SUPERIORE
Prof. Franco Palladino
Obiettivi formativi
Il corso è finalizzato alla trattazione di questioni matematiche elementari/fondamentali mediante l’applicazione di più
avanzate e recenti nozioni matematiche. Il senso e il titolo originario del corso traggono origine da F.Klein che, nella
seconda metà dell’Ottocento, corredò il suo insegnamento a riguardo con una serie di volumi.
Contenuti del corso
I cosiddetti “Problemi classici dell’antichità”. Algoritmi numerici “storici” e applicazioni informatiche.
Modalità di valutazione
Prova orale.
METODI PER IL TRATTAMENTO DELL’INFORMAZIONE
Prof.ssa Virginia Giorno
Obiettivi formativi
Il corso si prefigge in primo luogo di illustrare i concetti di base della programmazione orientata agli oggetti attraverso
lo studio del linguaggio di programmazione Java 2. In secondo luogo si intende fornire una conoscenza delle strutture
dati ponendo particolare enfasi sui collegamenti tra le strutture dati e i relativi algoritmi, includendo l’analisi della
complessità degli algoritmi considerati.
Contenuti del corso
Introduzione. Classi e oggetti. Tipi di dati fondamentali. Enunciato di decisione e di iterazione Elaborazione dei dati in
ingresso. Numeri casuali e simulazione. Progettazione di class. Pacchetti. Vettori e array.
Analisi di complessità
Liste concatenate Pile e code. Analisi di un problema: uscita da un labirinto.
Ricorsione. Backtraking. Analisi del problema delle otto regine. Alberi binari. La ricerca in un albero binario di ricerca.
Attraversamento, inserimento, eliminazione, e bilanciamento in un albero binario di ricerca.
Testi consigliati
- C.S. HORSTMANN (2002) Concetti di informatica e fondamenti di JAVA 2 (seconda edizione) Apogeo.
- A. DROZDEK (2001) Algoritmi e strutture dati in JAVA Apogeo.
Modalità di valutazione
Prova orale.
RICERCA OPERATIVA
Prof. Raffaele Cerulli
Obiettivi formativi
Al termine del corso ci si aspetta che lo studente abbia acquisito le competenze di base per la risoluzione di problemi
reali complessi mediante l’uso di modelli matematici di programmazione lineare e di ottimizzazione su rete.
Contenuti del corso
La programmazione lineare (PL):
• Definizione di poliedri; direzioni, direzioni estreme; teorema della rappresentazione; il metodo del simplesso:
punti estremi ed ottimalità; condizioni di ottimalità e illimitatezza. L'algebra del metodo del simplesso; la
ricerca di una soluzione ammissibile di base iniziale; il metodo delle due fasi; il metodo del Big M.
Degenerazione e cicli; convergenza del metodo del simplesso.
• Utilizzo di software applicativo per la modellazione e la soluzione di problemi di programmazione lineare.
• Dualità: formulazione del problema duale; costi ridotti; teorema debole e teorema forte della dualità; gli scarti
complementari; relazioni primale-duale; interpretazione economica del duale.
• Analisi della sensitività ed analisi parametrica: analisi postottimale; variazione della soluzione ottima e del
valore ottimo di un problema di PL al variare dei dati.
Ottimizzazione su rete:
• Problemi con matrice dei vincoli totalmente unimodulare
• Cammini minimi. Massimo flusso. Trasporto. Assegnamento.
Testi consigliati
• M.S. Bazaraa, J.J Jarvis & H.D. Sherali Linear Programming and Network Flows, Second Edition, John Wiley,
1990.
• Slides ed appunti delle lezioni.
Modalità di valutazione
Due prove in itinere scritte o pratiche. Esame finale orale.
SEMIGRUPPI LIBERI E TEORIA DEI CODICI
Prof.ssa Patrizia Longobardi
Obiettivi formativi
Scopo del corso è lo studio dei semigruppi e dei monoidi liberi, con particolare riferimento a proprietà delle parole su
un alfabeto, e di elementi della teoria generale dei codici.
Contenuti del corso
Generalità sui semigruppi. Il semigruppo delle relazioni in un insieme. Sottosemigruppi (sottomonoidi), congruenze,
quozienti, omomorfismi. Semigruppi ciclici. Il semigruppo sintattico.
Il semigruppo (monoide) delle parole su un insieme. Semigruppi (monoidi) liberi. Presentazioni dei semigruppi
(monoidi). Il monoide biciclico.
Parole coniugate. Parole infinite. Le parole infinite di Thue-Morse. Parole infinite libere da quadrati. Parole di Lyndon.
Generalità sui codici.. Proprietà combinatorie dei codici. Massimalità e completezza. Famiglie di codici e di
sottomonoidi di un semigruppo libero.
Testi consigliati
J. BERSTEL ˆ D. PERRIN ˆ Theory of Codes, Academic Press, London, 1985.
J. M. HOWIE ˆ An Introduction to Semigroup Theory, Academic Press, London, 1976.
G. LALLEMENT ˆ Semigroups and Combinatorial Properties, Wiley, New York, 1979.
M. LOTHAIRE ˆ Combinatorics on Words, Addison-Wesley, Reading, 1983.
Modalità di valutazione
Prova orale.
STORIA DELLE MATEMATICHE
Prof. Franco Palladino
Obiettivi formativi
Conoscenza del pensiero matematico da Euclide a Leibniz e Newton.
Contenuti del corso
Euclide, “Elementi”; Bombelli, “Algebra”; Galilei, Cartesio, Fermat, Leibniz e Newton.
Testi consigliati
Ch. Boyer, “Storia della Matematica”, Milano, Mondatori.
brani delle opere originali.
Modalità di valutazione
Prova orale.
TEORIA DEI GRAFI
Prof. Francesco Bottacin
Obiettivi formativi
L’obiettivo del corso è quello di presentare le idee e le tecniche principali utilizzate nello studio della teoria dei grafi e
discutere alcune delle applicazioni della teoria dei grafi a altre discipline.
Contenuti del corso
Definizioni e proprietà elementari dei grafi. Matrici associate a un grafo: matrice di adiacenza e matrice di incidenza. Il
primo teorema della teoria dei grafi. Isomorfismi e automorfismi dei grafi. Operazioni elementari sui grafi: unione,
intersezione, differenza, etc.
Sottografi, sottografi indotti e sottografi generanti. Il grado dei vertici. Grafi regolari. Il teorema di König.
Cammini e cicli in un grafo: definizioni e principali risultati. Passeggiate e percorsi in un grafo. Calcolo del numero di
passeggiate tra due vertici attraverso la matrice di adiacenza.
Grafi connessi. Le componenti di un grafo. Il teorema di Mader (senza dimostrazione).
Alberi e foreste. Caratterizzazione degli alberi. Alberi radicati. Alberi radicati normali e alberi normali generanti.
Grafi bipartiti e grafi r-partiti. Contrazioni e minori. Suddivisioni e minori topologici.
Cammini Euleriani. Il teorema di Eulero.
Altre nozioni di grafo: ipergrafi, grafi diretti (digrafi), grafi orientati, multigrafi.
Grafi planari. Grafi massimamente piani e triangolazioni piane. La formula di Eulero. Grafi planari e poliedri. I cinque
poliedri regolari.
Caratterizzazione dei grafi planari. Il teorema di Kuratowski.
Colorazioni di grafi. Colorazioni dei vertici e colorazioni dei lati di un grafo. Il numero cromatico e l'indice cromatico.
Colorazioni dei grafi planari: il teorema dei quattro colori (senza dim.), il teorema dei cinque colori. Relazioni tra il
numero cromatico e altri invarianti di un grafo. Algoritmi per la colorazione dei vertici.
Testi consigliati
R. Diestel, ''Graph Theory'', Springer-Verlag, Electronic Edition, 2000.
G. Chartrand, L. Lesniak, ''Graphs & Digraphs'', Chapman & Hall.
Modalità di valutazione
Esame orale e/o preparazione di una lezione su un argomento non trattato durante il corso.
TEORIA DEI NUMERI
Prof.ssa Patrizia Longobardi
Obiettivi formativi
Scopo del corso è lo studio di proprietà classiche dei numeri interi. Saranno inoltre illustrati esempi e applicazioni, e
verrà fornito qualche cenno storico.
Contenuti del corso
Richiami sulla divisibilità nell'insieme dei numeri naturali e dei numeri interi. Distribuzione dei numeri primi, primi di
Fermat, primi di Mersenne.
Equazioni diofantine.
Richiami sulle congruenze nell'insieme dei numeri interi. Congruenze lineari, sistemi. Il teorema di Lagrange.
Pseudoprimi e numeri di Carmichael.
Radici primitive.
Funzioni aritmetiche. Numeri perfetti.
Residui quadratici e teorema di reciprocità. Somme di quadrati. L'equazione pitagorica.
Osservazioni sull'Ultimo teorema di Fermat.
Elementi di crittografia.
Testi consigliati
G. A. JONES ˆ J. M. JONES ˆ Elementary Number Theory, Springer, 1998 (rist. 2003).
Modalità di valutazione
Prova orale.
TEORIA DELLA COMPUTABILITÀ I
Prof. Giangiacomo Gerla
Propedeuticità
E’ opportuno che si siano superati gli esami del primo anno e che si conosca almeno un linguaggio di programmazione.
Obiettivi formativi
• Conoscenza di alcune nozioni teoriche di informatica quali le macchine a registri, gli automi, la decidibilità, i
sistemi di riscrittura
• Conoscenza dei limiti teorici delle macchine calcolatrici
• Capacità di inquadrare le tecniche di programmazione in un ambito teorico generale
Contenuti del corso
Algoritmi e macchine. Macchine a memoria finita, gli automi. Cose che un automa finito non può fare (la
moltiplicazione, l’estrazione di radice). Costruire automi tramite il teorema di completezza funzionale per algebre di
Boole. Porte logiche, reti sequenziali, reti combinatorie. Macchine a memoria infinita, linguaggi di programmazione
evoluti, funzioni ricorsive, Tesi di Church. Insiemi decidibili, insiemi ricorsivamente enumerabili, macchine universali.
Cose che una macchina a memoria infinita non può fare, il teorema della fermata, il teorema di Rice. Sistemi di
riscrittura e calcolo simbolico.
Testi consigliati
Appunti dal corso scaricabili da http://www.dmi.unisa.it/people/gerla/www/
Manuale del linguaggio Mathematica
M. Minsky, Computation, finite and infinite machines, Prentice-Hall International, INC., London.
A.J. Kfoury, R.N. Moll, M.A. Arbib, Programmazione e computabilità, ETAS libri, 1986.
R. Cordeschi, La scoperta dell'artificiale, Dunod, Milano.
Y. Castelfranchi e O. Stock, "Macchine come noi", Laterza.
Modalità di valutazione
Prova orale e prove in laboratorio.
TEORIA DELL’INFORMAZIONE
Prof.ssa Virginia Giorno
Obiettivi formativi
Il corso si prefigge di fornire gli elementi di base per la modellizzazione di un sistema di comunicazione
unidimensionale in cui l'informazione è trasmessa dalla sorgente alla destinazione attraverso un canale di trasmissione
generalmente soggetto a rumore aleatorio.
Contenuti del corso
Descrizione di un sistema di comunicazione unidimensionale.
Misure di informazione: Autoinformazione e mutua informazione. Entropia di una variabile aleatoria. Entropia
congiunta e condizionata. Mutua informazione media. Entropia di vettori aleatori. Mutua informazione media di vettori
aleatori. Funzioni convesse e disuguaglianza di Jensen. Teorema di elaborazione dei dati.
Sorgenti di informazione: Sorgenti discrete stazionarie senza memoria. Teoremi di codifica in assenza di rumore sul
canale. Algoritmo di Huffman. Sorgenti di informazione discrete con memoria.
Canali: Canali finiti stazionari senza memoria. Capacità informazionale e sua valutazione. Criteri di decodifica.
Codifica in presenza di rumore sul canale. Teoremi di codifica di Shannon.
Codici correttori d'errore: Codici lineari e di Hamming.
Testi consigliati
- COVER M. C. and THOMAS J. A. - Elements of Information Theory - John Wiley & Sons, Inc.
- FABRIS F. - Teoria dell’Informazione, codici, cifrari – Boringhieri.
- GALLAGER R. - Information Theory and Reliable Communication - J. Wiley.
Modalità di valutazione
Prova orale.
TEORIA DELL’INFORMAZIONE II
Prof.ssa Virginia Giorno
Obiettivi formativi
Il corso si prefigge di fornire alcune metodologie per la descrizione dell’evoluzione di sistemi dinamici. Particolare
enfasi è dedicata agli aspetti teorici presentati mediante alcune applicazioni.
Contenuti del corso
Richiami di Calcolo delle Probabilità: Funzioni generatrici e funzioni caratteristiche e loro utilizzo. Processi
stocastici: definizioni e proprietà. Esempi.
Sorgenti con memoria: Catene di Markov. Distribuzione limite e distribuzioni invarianti per catene di Markov.
Calcolo dell’entropia per catene di Markov. Sorgenti di Markov unifilari. Calcolo dell’entropia. Teorema di codifica per
sorgenti di Markov.
Modelli di crescita: Crescita malthusiana. Crescita logistica. Crescita di Gompertz. Modelli preda-predatore. Modelli
stocastici di crescita. Applicazioni a sistemi di crescita tumorale.
Modelli di attività neuronale: Potenziale di membrana e relativa rappresentazione attraverso processi di diffusione.
Modello di Wiener. Modello di Ornstein-Uhlenbeck. Il tempo di sparo come tempo di primo passaggio. Densità di
sparo.
Testi consigliati
- F. Fabris (2001) Teoria dell’Informazione, codici, cifrari. Bollati Boringhieri.
- S.M. Ross (1989) Introduction to probability models. Academic Press.
- Appunti delle lezioni.
Modalità di valutazione
Prova orale.
TEORIA DELLE FUNZIONI
Prof. Vittorio Cafagna
Obiettivi formativi
Scopo del corso è familiarizzare gli studenti con le differenti classi di funzioni utilizzate in diversi rami della
matematica e discutere il paradigma dell'organizzazione dei diversi spazi funzionali secondo la teoria della
stratificazione naturale. Due esempi significativi (funzioni differenziabili secondo la struttura dei punti critici e
polinomi ortogonali secondo la struttura degli zeri) sono svolti in dettaglio.
Contenuti del corso
Revisione dei prerequisiti: algebra elementare (gruppi , anelli, spazi vettoriali), topologia generale (compattezza e
convergenze), calcolo differenziale in più variabili (determinanti Jacobiani, teorema del rango), serie (teorema di
Fourier, funzioni analitiche).
Esempio guida: stratificazione dello spazio delle matrici quadrate.
Concetto di funzione e generalizzazioni.
Spazi di funzioni e di funzioni generalizzate: aspetti algebrici e analitici. Esempi: polinomi, funzioni analitiche, serie
formali, funzioni algebriche, funzioni differenziabili, funzioni continue, funzioni misurabili, misure di Radon,
distribuzioni. Ideali e teorema degli zeri di Hilbert.
Sistemi ortogonali. Autofunzioni di problemi di Sturm-Liouville. Polinomi ortogonali. Autofunzioni dell'operatore di
Laplace-Beltrami sulle varietà riemanniane compatte. Esempi: funzioni trigonometriche in più variabili, armoniche
sferiche.
Topologie sugli spazi di funzioni. Trasversalità e genericità. Variazioni sul lemma di Sard. Funzioni di Morse. Zeri
trasversi di polinomi ortogonali.
Indici numerici: grado, numeri di intersezione, caratteristiche di Eulero, indice di Morse, numero di oscillazione di
Sturm, numero di insiemi nodali. Teorema di Courant e generalizzazioni. Congettura di Yau.
Strumentario topologico-differenziale: teorema di h-cobordismo di Smale, teorema di preparazione di WeierstrassMalgrange, teorema di pseudoisotopia di Thom, teorema di divisione di Hörmander-Malgrange-Losiacewicz.
Singolarità di mappe differenziabili. Catalogo delle catastrofi elementari.
Teoria elementare delle stratificazioni. Condizioni di Whitney e di Thom.
Applicazioni: stratificazione naturale dello spazio delle funzioni differenziabili (teoria di Thom-Mather-Cerf);
stratificazioni deboli dello spazio dei polinomi ortogonali sul cerchio unitario.
Problemi aperti e prospettive di ricerca.
Testi consigliati
Hirsch, M., Differential Topology, Springer, New York-Heidelberg-Berlin, 1976.
Modalità di valutazione
Prova orale.
PROGRAMMI DEL CORSO DI LAUREA
SPECIALISTICA IN MATEMATICA
ALGEBRA III
Prof. Giovanni Vincenzi
6 CFU
SSD MAT/02
Obiettivi formativi
Questo corso è dedicato allo studio della teoria di Galois sulla risoluzione per radicali delle equazioni algebriche su di
un campo.
Contenuti del corso
Richiami di teoria dei campi. Gruppi di automorfismi di un campo. Richiami sui gruppi risolubili. Estensioni normali ed
estensioni separabili di un campo.
Grado di separabilità di un’estensione. Estensioni di Galois: estensioni binomie; estensioni ciclotomiche. Equazioni
risolubili per radicali: teorema di Galois, teorema di Artin-Schreier.Teorema di Ruffini-Abel. Norma e traccia di
un’estensione di Galois. Estensioni cicliche: il teorema 90 di Hilbert. Approfondimenti: teoria di Jacobson Bourbaki,
teoria dei corpi.
Testi consigliati
Appunti distribuiti durante il corso.
Modalità di valutazione
Prova orale.
ALGEBRA IV
Prof.ssa Mercede Maj
6 CFU
SSD MAT/02
Obiettivi formativi
Scopo di questo corso è di approfondire lo studio della teoria dei moduli su di un anello unitario. Vengono inoltre
illustrati risultati di teoria dei numeri cardinali e ordinali e di teoria delle categorie.
Contenuti del corso
Numeri cardinali e ordinali.
Categorie e funtori.
Teoria dei moduli: esempi, somme e prodotti diretti di una famiglia di moduli, moduli semplici, moduli fedeli, moduli
periodici e aperiodici.
Moduli liberi, moduli proiettivi , iniettivi, divisibili.
Moduli su di un anello principale.
Prodotto tensoriale.
Testi consigliati
M. CURZIO, P. LONGOBARDI, M. MAJ - Lezioni dai Algebra - Liguori Editore, Napoli, 1994.
T.W. HUNGERFORT - Algebra - Springer-Verlag, Berlin, 1974.
T.S. BLYTH - Module Theory, Clarendon Press, Oxford, 1990.
Modalità di valutazione
Prova orale.
ALGEBRA UNIVERSALE E
TEORIA DEI MODELLI
Prof. Antonio Di Nola
6 CFU
SSD MAT/01
Obiettivi formativi
Impadronirsi della nozione di teoria equazionale e delle principali tecniche di algebra universale. Impadronirsi della
nozione di ultraprodotto e delle sue principali applicazioni alla Logica.
Contenuti del corso
Algebra Universale:
Algebre e omomorfismi. Congruenze. Primo teorema di isomorfismo. Prodotti diretti. Prodotto sottodiretto. Teorema di
Birkhoff. Varietà. Teorema di Tarsi. Algebra dei termini. Algebre libere. Equazioni
Teoria dei Modelli:
Linguaggi non numerabili. Linguaggi non numerabili: definizioni e prime proprietà. Strutture relazionali (di dato tipo).
Strutture relazionali, sottostrutture, estensioni, restrizioni. Omomorfismi e immersioni fra strutture relazionali.
Equivalenza elementare. Sottostrutture elementari, estensioni elementari, immersioni elementari. Criteri per la
determinazione di estensioni elementari. Enumerazioni. Criteri per la determinazione di equivalenze elementari.
Teoremi di Lowenheim-Skolem I, II. Teorema di Compattezza del Calcolo dei Predicati.
Ultraprodotti:
Definizione di prodotto ridotto e ultraprodotto di strutture relazionali. Teorem di Łos. Finita assiomatizzabilità.
Proprietà generali del primo ordine. Teorema di completezza di Goedel-Henkin.
Testi consigliati
• Appunti dal corso.
•
•
J.L. Bell- A.B. Slomson, Models and Ultraproducts.
C.C. Chang, H.J. Keisler, Model Theory.
Modalità di valutazione
Prova orale.
ANALISI FUNZIONALE I
Prof.ssa Luciana Sgambati
6 CFU
SSD MAT/05
Obiettivi formativi
Scopo del corso è lo studio dei problemi istituzionali dell’Analisi Funzionale.
Contenuti del corso
Teoremi fondamentali di analisi lineare (Hahn-Banach, applicazione aperta, uniforme limitatezza, grafico chiuso).
Topologie deboli e spazi convessi.
Testi consigliati
H. BREZIS, Analisi Funzionale, Liguori Editore.
Modalità di valutazione
Prova orale.
ANALISI FUNZIONALE II
Prof.ssa Luciana Sgambati
3 + 3 CFU
SSD MAT/05
Obiettivi formativi
Scopo del corso è lo studio dei problemi istituzionali dell’Analisi Funzionale.
Contenuti del corso
Spazi Lp
Spazi di Sobolev in dimensione uno.
Testi consigliati
H. BREZIS, Analisi Funzionale, Liguori Editore.
Modalità di valutazione
Prova orale.
ANALISI MATEMATICA V
Prof. Antonio Vitolo
6 CFU
SSD MAT/05
Obiettivi formativi
Ampliamento delle conoscenze matematiche di base: fondamenti della teoria delle funzioni di variabile complessa,
relative tecniche di calcolo e introduzione ad alcuni settori di applicazione.
Contenuti del corso
1. Rappresentazioni del piano complesso.
2. Funzioni olomorfe e teorema integrale di Cauchy.
3. Formula integrale di Cauchy e applicazioni.
4. Serie di funzioni in campo complesso.
5. Serie di Taylor e zeri delle funzioni olomorfe.
6. Serie di Laurent e classificazione delle singolarità isolate.
7. Teoria dei residui e principio dell’argomento.
8. Funzioni speciali: funzione Gamma di Eulero e funzioni di Bessel.
9. Serie di Dirichlet e funzione Zeta di Riemann.
Testi consigliati
D. GRECO, Complementi di Analisi Matematica, Liguori (NA).
J.B. CONWAY, Complex Analysis, Springer-Verlag.
Modalità di valutazione
Prova scritta e discussione orale.
ANALISI MATEMATICA VI
Prof. Antonio Vitolo
6 CFU
SSD MAT/05
Obiettivi formativi
Ampliamento delle conoscenze matematiche di base e introduzione all’uso di metodi matematici di livello superiore:
teoria della misura e dell’integrazione di Lebesgue, nonché spazi di funzioni sommabili; spazi di Banach e di Hilbert;
analisi di Fourier.
Contenuti del corso
1. Spazi di Banach di funzioni limitate e di funzioni continue.
2. Teoria della misura.
2. Integrazione in spazi di misura.
P
4. Spazi L : disuguaglianza di Hölder, completezza, approssimazione con funzioni regolari.
5. Spazi di Hilbert: decomposizione ortogonale, rappresentazione delle forme lineari, sistemi
ortonormali, modelli ed esempi in dimensione infinita.
6. Funzioni periodiche e integrale di Riemann.
7. Serie di Fourier: convergenza puntuale, uniforme, integrazione termine a termine.
1
8. Trasformata di Fourier in L : proprietà formali ed effetto regolarizzante.
9. Formula di inversione della trasformata di Fourier e applicazione alle equazioni differenziali.
2
10. Trasformata di Fourier in L e teorema di Plancherel.
Testi consigliati
G. GIUSTI, Analisi Matematica II, Boringhieri (FI).
H. BREZIS, Analisi Funzionale, Liguori (NA).
A. TESEI, Istituzioni di Analisi Superiore, Boringhieri (FI).
W. RUDIN, Analisi reale e complessa, Boringhieri (FI).
Modalità di valutazione
Prova scritta e discussione orale.
ANALISI NUMERICA (avanzata)
Prof.ssa Elvira Russo
6 CFU
SSD MAT/08
Obiettivi formativi
Il corso è finalizzato a mettere lo studente in grado di acquisire competenze per la risoluzione numerica di problemi
modellizzate da equazioni alle derivate parziali, nonché per sviluppare software matematico ad architettura parallela.
Contenuti del corso
METODI ALLE DIFFERENZE FINITE PER EQUAZIONI DIFFERENZIALI ALLE DERIVATE PARZIALI.
Generalità sul trattamento numerico: idea base dei metodi agli elementi finiti e dei metodi alle differenze finite.
Equazioni ellittiche: Metodi alle differenze finite. Consistenza. Errore di troncamento. Stima dell'errore. Convergenza.
Equazioni paraboliche: Schemi impliciti ed espliciti. Consistenza. Convergenza. Stabilità. Teorema di Lax. Metodo
delle linee. Metodi numerici per la risoluzione del sistema di equazioni differenziali ordinarie risultante.
Equazioni iperboliche: Equazione delle onde, soluzione analitica. Domini di dipendenza ed influenza. Metodi alle
differenze finite. Consistenza. Stabilità. Condizione di Courant per la convergenza.
Architetture parallele. Tecniche di parallelizzazione: Divide et impera, Recursive doubling, Iterazioni vettoriali,
Vettorizzazione. Indici di valutazione di un algoritmo parallelo. Parallelismo SIMD e MIMD. Metodi paralleli diretti ed
iterativi per la risoluzione di sistemi lineari. Il sistema MPI.
Testi consigliati
E.Isaacson, H.Keller, Analysis of numerical methods, J.Wiley Sons.
MPI Manuale.
Modalità di valutazione
Per studenti che svolgono con profitto il corso: test di verifica, progetto, colloquio finale.
Per studenti che non hanno svolto con profitto il corso o che non hanno preso parte al corso: progetto e colloquio finale.
ANALISI SUPERIORE
Prof.ssa Maria Transirico
6 CFU
SSD MAT/05
Obiettivi formativi
Il corso di Analisi Superiore è dedicato essenzialmente allo studio degli spazi metrici e degli spazi di Banach, nonché
allo studio dell’integrale di Lebesgue.
Gli obiettivi formativi del corso consistono nell’acquisizione dei risultati e delle tecniche dimostrative.
Contenuti del corso
1. Spazi metrici. Spazi normati.
2. Spazi metrici completi. Spazi di Banach.
3. Funzioni Lipschitziane.
4. Insiemi compatti. Teoremi di compattezza.
5. Aperti connessi dello spazio euclideo n-dimensionale.
6. Misura di Lebesgue.
7. Integrale di Lebesgue.
8. Spazi di Lebesgue.
Testi consigliati
N. FUSCO - P. MARCELLINI - C. SBORDONE, Analisi Matematica due, Liguori Editore.
H. BREZIS, Analisi Funzionale, Liguori Editore.
W. RUDIN, Analisi reale e complessa, Boringhieri.
Metodi di valutazione
Sono previsti, di norma, un seminario e una prova orale.
CALCOLO DELLE
PROBABILITA’ E STATISTICA
Prof. Antonio Di Crescenzo
3 CFU
SSD MAT/06
Obiettivi formativi
Conoscenze di livello medio di teoria della probabilità. Essere in grado di risolvere problemi che richiedono l’utilizzo
degli strumenti di tale teoria.
Contenuti del corso
Probabilità
Spazio di probabilità. Probabilità condizionata. Indipendenza. Primi teoremi della probabilità.
Variabili aleatorie
Variabili aleatorie. Funzioni di ripartizione e relative proprietà. Variabili aleatorie discrete ed assolutamente continue.
Valore atteso, varianza, momenti. Principali distribuzioni di probabilità. Vettori aleatori. Funzioni di ripartizione
multiple. Indipendenza. Covarianza e correlazione.
Teorema centrale di convergenza
Funzione generatrice dei momenti. Funzione caratteristica. Disuguaglianza di Chebyshev. Criteri di convergenza per
successioni di variabili aleatorie. Legge dei grandi numeri. Teorema centrale di convergenza.
Processi stocastici
Generalità. Processi di Marcov. Processo di Poisson. Catene di Markov. Processo di moto Browniano. Applicazioni.
Testi consigliati
DALL'AGLIO G. (2000) Calcolo delle Probabilità. II edizione. Zanichelli.
ROSS G. (1996) Stochastic Processes. II edizione. John Wiley & Sons.
Modalità di valutazione
Prova orale.
CALCOLO NUMERICO II
6 CFU
SSD MAT/08
Prof.ssa Elvira Russo
Obiettivi formativi
Il corso è finalizzato a mettere lo studente in grado di acquisire competenze per la risoluzione numerica di problemi
modellizzati da equazioni differenziali ordinarie, nonché per sviluppare software matematico di qualità.
Contenuti del corso
METODI NUMERICI PER EQUAZIONI DIFFERENZIALI ORDINARIE.
Metodi di approssimazione di tipo analitico. Metodi lineari multistep. Metodi predictor-corrector. Metodi BDF. Metodi
non-lineari ad un passo. Metodi di Runge-Kutta. Ordine. Stime degli errori. Consistenza. Convergenza. Zero-stabilità.
Teoria della debole stabilità. Sistemi stiff. Struttura di un algoritmo a passo variabile. Procedure di starting. Stima
dell’errore di troncamento. Strategie per il cambiamento del passo. Valutazione del software.
Testi consigliati
E.Hairer, S.P.Norsett, G.Wanner - Solving Ordinary Differential Equations -I.S.C.M. Springer Verlag.
J.B.Lambert - Computational methods in Ordinary Differential Equations - J.Wiley Sons.
Metodi di valutazione
Per studenti che svolgono con profitto il corso: test di verifica, prova di laboratorio, progetto, colloquio finale.
Per studenti che non hanno svolto con profitto il corso o che non hanno preso parte al corso: progetto e colloquio finale.
ELEMENTI DI FISICA MODERNA
Prof. Mario Fusco Girard
4 CFU
SSD FIS/01
Obiettivi formativi
Il corso si propone di introdurre lo studente allo studio matematico delle onde e dei fenomeni connessi, con particolare
riferimento al caso delle onde elettromagnetiche; ciò permette in seguito lo studio della teoria della relatività ristretta.
Infine, vengono presentate le idee fondamentali della meccanica quantistica.
Contenuti del corso
Equazione di d’Alembert. Integrale di d’Alembert. Onde sinusoidali. Interferenza. Separazione di variabili per
l’equazione di d’Alembert. Onde in più dimensioni spaziali. Principio di Huyghens. Diffrazione. Esperimento di Young.
Effetto Doppler. Operatori differenziali in coordinate curvilinee. Equazione delle onde in coordinate polari piane.
Equazione e funzioni di Bessel. Onde elettromagnetiche piane. Ottica geometrica e principio di Fermat. Polarizzazione.
Potenziali elettromagnetici. Equazione d’onda non omogenea. Sviluppi in serie ed in integrale di Fourier. Funzione di
Dirac. Funzione di Green. Potenziali ritardati. Trasformazioni di Lorentz. Cinematica relativistica. Quadrivettori e
quadritensori. Meccanica relativistica. Introduzione alla meccanica quantistica. Equazione di Schroedinger.
Testi consigliati
L.Landau, E. Lifchits: Teoria dei Campi. Editori Riuniti.
L.Landau. E. Lifchits : Meccanica Quantistica. Editori Riuniti.
Modalità di valutazione
Esame finale.
EQUAZIONI DIFFERENZIALI
Prof.ssa Anna Canale
6 CFU
SSD MAT/05
Obiettivi formativi
Il corso tratta vari aspetti legati allo studio delle equazioni differenziali. Lo scopo è quello di ottenere che lo studente
abbia un buon livello di chiarezza e conoscenza delle tematiche trattate e sviluppi una capacità di sintesi che lo aiuti ad
affrontare le problematiche che incontra nel corso dei suoi studi.
Contenuti del corso
Teoria delle equazioni differenziali. Equazioni lineari. Problemi ai limiti. Analisi qualitativa delle soluzioni. Equazioni
esatte. Metodi risolutivi di equazioni differenziali. Sistemi di equazioni differenziali.
Testi consigliati
N. Fusco - P. Marcellini - C. Sbordone, Analisi Matematica II, Liguori Editore.
E. Giusti, Analisi Matematica 2, Boringhieri Editore.
F. Conti, Calcolo, McGraw-Hill Libri Italia.
F. Conti - P. Aquistapace - A.Savoini, Analisi Matematica. Teoria e Applicazioni, McGraw-Hill Libri Italia.
P. Marcellini - C. Sbordone, Esercitazioni di Analisi Matematica, Volume II, parte prima, Liguori Editore.
Modalità di valutazione
Preparazione di una tesina ed esame orale.
FISICA MATEMATICA II
Prof. Ettore Laserra
6 CFU
SSD MAT/07
Obiettivi formativi
Fornire una buona conoscenza dei fondamenti e dei metodi della Fisica Matematica, in particolare della Meccanica
Analitica e del Calcolo delle Variazioni.
Contenuti del corso
ELEMENTI DI CALCOLO DELLE VARIAZIONI.
LA MECCANICA DI LAGRANGE (MECCANICA ANALITICA): Varietà differenziabili. Fibrati tangenti. Campi
vettoriali. Forme differenziali. Sistemi olonomi. Le equazioni di Lagrange. Meccanica riemanniana. Sistemi
lagrangiani. Integrali primi. Il principio dell’azione stazionaria.
LA MECCANICA DI HAMILTON (MECCANICA SIMPLETTICA): Fibrati cotangenti e sistemi hamiltoniani. La
trasformazione di Legendre. Il metodo di Jacobi. Parentesi di Poisson e integrali primi. Sottovarietà lagrangiane. Varietà
simplettiche e sistemi hamiltoniani integrabili.
Testi consigliati
S. BENENTI, Modelli matematici della Meccanica, vol. I, Celid.
V.I. SMIRNOV, Corso di Matematica Superiore, vol. 4, tomo 1, Mir.
Modalità di valutazione
Per studenti che svolgono con profitto il corso: prova intercorso.
FONDAMENTI DI GEOMETRIA
Prof. Francesco Bottacin
3 CFU
SSD MAT/03
Obiettivi formativi
L’obiettivo del corso è quello di descrivere a grandi linee lo sviluppo storico della geometria, da Euclide fino ai giorni
nostri, soffermandosi sulle idee principali che, in varie epoche, hanno rivoluzionato lo studio della geometria.
Contenuti del corso
Gli ''Elementi'' di Euclide. Analisi della struttura dell'opera, con particolare riferimento al Libro I.
Il problema dell'indipendenza e della non contraddizione degli assiomi.
''I Principi Fondamentali della Geometria'' di Hilbert. Analisi della struttura dell'opera, con particolare riferimento al
Capitolo 1. Il problema dell'indipendenza e della non contraddizione degli assiomi, e la soluzione proposta da Hilbert. Il
fallimento del programma di Hilbert. I teoremi di incompletezza di Gödel (brevi cenni di Logica Matematica).
Introduzione alle geometrie non euclidee. La geometria ellittica di Riemann. La geometria iperbolica di Lobachevski. I
tre modelli del piano iperbolico: il modello di Klein, il modello del disco unitario
di Poincaré e il modello del semipiano superiore. Studio della geometria iperbolica nel modello del semipiano
superiore. Le rette nel piano iperbolico. Le isometrie del piano iperbolico. I triangoli nel piano iperbolico. Criteri per la
congruenza dei triangoli. L'area di un triangolo. La somma degli angoli interni di un triangolo. Il modello del disco
unitario di Poincaré. La metrica iperbolica nel modello del disco unitario.
I cerchi nel piano iperbolico (nei modelli del disco unitario e del semipiano superiore). La lunghezza della circonferenza
e l'area di un cerchio di raggio R. Cicli, orocicli e ipercicli.
Una breve introduzione alle idee e ai metodi che stanno alla base della geometria algebrica moderna.
Spazi affini e varietà affini su un corpo K. Ideale associato a una varietà affine e anello delle funzioni regolari. Ideali
radicali e ideali primi. Dimensione di una varietà affine e dimensione di Krull di un anello.
Morfismi di varietà e omomorfismi di anelli. Schemi affini: lo spettro di un anello commutativo con unità.
Testi consigliati
Gli Elementi di Euclide.
I Principi Fondamentali della Geometria di Hilbert.
E.E. Moise, ''Elementary Geometry from an Advanced Standpoint'', Addison-Wesley, Reading MA, 1974.
E. Agazzi, ''Le Geometrie Non Euclidee''.
A. Ramsay, ''Introduction to Hyperbolic Geometry''.
G.E. Martin, ''The Foundations of Geometry''.
R. Bonola, ''Non-Euclidean Geometry''.
M.J. Greenberg, ''Euclidean and Non-Euclidean Geometries'', Freeman & Company, New York, 1974.
Modalità di valutazione
Esame orale e/o preparazione di una lezione su un argomento non trattato durante il corso.
GEOMETRIA IV
Prof. Alexandre Vinogradov
6 CFU
SSD MAT/03
Obiettivi formativi
Obiettivo principale del corso è introdurre lo studente ai concetti di base e ai metodi della geometria differenziale su
materiale più semplice possibile, e sviluppare le capacità di interpretazione geometrica di materiale algebrico e analitico
e viceversa.
Contenuti del corso
Il corso è suddiviso in tre parti. La prima, introduttiva, contiene il necessario materiale preliminare: una sintesi di
geometria affine e di topologia naturale degli spazi euclidei, l’interpretazione geometrica di alcuni elementi del calcolo
differenziale di funzioni di più variabili. La seconda parte è un percorso che parte dallo studio generale delle
sottovarietà negli spazi affini e finisce con l’introduzione delle varietà astratte. La terza parte è dedicata alla teoria
metrica delle curve negli spazi euclidei multi-dimensionali. Include la teoria degli spazi oscuratori di una curva, n-edro
mobile di Fernet, curvature superiori di una curva e metodi del loro calcolo. I punti centrali qui sono due teoremi
fondamentali: il primo, sulla forma di una curva e il secondo sulla realizzazione delle curvature assegnate a priori.
Testi consigliati
Appunti del corso.
Modalità di valutazione
Colloquio preliminare ed esame orale.
GEOMETRIA V
Prof. Alexandre Vinogradov
6 CFU
SSD MAT/03
Obiettivi formativi
Obiettivo principale del corso è introdurre lo studente ai concetti di base e ai metodi della geometria differenziale su
materiale più semplice possibile, e sviluppare le capacità di interpretazione geometrica di materiale algebrico e analitico
e viceversa.
Contenuti del corso
Il corso è la continuazione naturale di Geometria IV ed è dedicato principalmente alla geometria metrica delle
sottovarietà di spazi Euclidei. Attenzione speciale si dà alla distinzione fra la geometria esterna di una sottovarietà e
quella interna. Quest’ultima fornisce un percorso naturale per introdurre l’idea della geometria Riemanniana astratta alla
fine del corso. Elementi di base della geometria metrica si sviluppano per le sottovarietà generali mentre i risultati più
concreti che richiedono alcune tecniche più delicate si dimostrano solo per le superfici. In particolare, si discutono le
equazioni di Gauss-Wiengarten, il “teorema egregio” di Gauss, proprietà estreme delle curve geodetiche, la
classificazione delle superfici di curvatura di Gauss costante ed il problema del “quinto postulato”.
Testi consigliati
Appunti del corso.
Modalità di valutazione
Colloquio preliminare ed esame orale.
GEOMETRIA VI
Prof.ssa Anna Di Concilio
6 CFU
SSD MAT/03
Obiettivi formativi
Lo scopo del corso di Geometria VI consiste nell’ introdurre allo studio della topologia algebrica e nel dare un
esempio di classificazione: il teorema di classificazione topologica delle superfici connesse e compatte con e senza
bordo.
Contenuti del corso
Omotopia tra funzioni e tra spazi. Retratti e retratti per deformazione. Connessione semplice. Omotopia di cammini. Il
gruppo fondamentale. Calcolo del gruppo fondamentale della circonferenza. Metodi di calcolo del gruppo
fondamentale. Applicazioni: il teorema fondamentale dell’algebra, il teorema del punto fisso in dimensione due.
Superfici. Superfici con bordo. Somma connessa di superfici. Forma canonica di una somma connessa di tori e di piani
proiettivi reali. Sfere con manici. Triangolazioni. Caratteristica di Eulero-Poincaré. Orientabilità e non. Classificazione
topologica delle superfici connesse e compatte con o senza bordo.
Testi consigliati
R. Engelking, General Topology, PWN Polish scientific Publishers 1998.
C. Godbillon, Elements of Topologie Algebrique, Collection Methodes Hermann Paris 1971.
W.S. Massey, Algebraic Topology : An Introduction, Springer-Verlag 1991.
S. Willard, General Topology, Addison-Wesley publishing Company 1970.
Modalità di valutazione
Prova orale.
GEOMETRIA ALGEBRICA
Prof. Francesco Bottacin
3 CFU
SSD MAT/03
Obiettivi formativi
L’obiettivo del corso è quello di fornire un’introduzione moderna alla geometria algebrica.
Contenuti del corso
Varietà affini e proiettive. Morfismi di varietà. Funzioni regolari e funzioni razionali. Isomorfismi e applicazioni
birazionali. Introduzione del concetto di schema algebrico.
Alcuni argomenti specifici verranno scelti di volta in volta, di comune accordo con gli studenti.
Testi consigliati
R. Hartshorne, “Algebraic Geometry”, Springer-Verlag.
Modalità di valutazione
Esame orale e/o preparazione di una lezione su un argomento non trattato durante il corso.
ISTITUZIONI DI FISICA
MATEMATICA
Prof. Ettore Laserra
6 CFU
SSD MAT/07
Obiettivi formativi
Fornire una buona conoscenza dei fondamenti e dei metodi della Fisica Matematica, in particolare del Calcolo
Tensoriale, della Meccanica dei Continui e delle equazioni alle derivate parziali della Fisica Matematica.
Contenuti del corso
CALCOLO TENSORIALE: Notazione con indici. Tensori e trasformazioni. Esempi. Derivate tensoriali. Geometria
differenziale.
MECCANICA DEI CONTINUI.
EQUAZIONI ALLE DERIVATE PARZIALI DELLA FISICA MATEMATICA.
Testi consigliati
G. Caricato, "Elementi di meccanica dei continui", Cisu.
J.H. Heinbockel, “Introduction to Tensorial Calculus and Continuum Mechanics”, Trafford Publishing.
L. Amerio, “Analisi Matematica con elementi di Analisi Funzionale”, Vol. 3, Parte II, Utet.
V.P. Michajlov, " Equazioni alle Derivate Parziali", Edizioni Mir.
Modalità di valutazione
Per studenti che svolgono con profitto il corso: prova intercorso.
LABORATORIO DI MATEMATICA
COMPUTAZIONALE
Dott.ssa Dajana Conte
3 CFU
SSD MAT/08
Obiettivi formativi
Scopo del corso è mostrare allo studente la possibilità di utilizzare un ambiente di calcolo scientifico per visualizzare,
fare ipotesi, prevedere andamenti, trovare risultati inerenti argomenti già trattati nei corsi di base del primo anno. Il
corso è organizzato in unità didattiche indipendenti.
Contenuti del corso
Significati geometrici: uso delle primitive del Mathematica per analizzare approssimazioni locali e globali, per
visualizzare l’approssimazione dei minimi quadrati, per scoprire interessanti proprietà della funzione esponenziale.
Calcoli numerici: scoprire l’andamento di successioni e serie. Prove numeriche e visualizzazioni con il Matematica.
Calcolo simbolico: avanzare ipotesi e dimostrare teoremi con l’uso delle primitive simboliche del Mathematica. Un
caso particolare: l’ordine di infinito del fattoriale.
Il sistema Mathematica: linguaggio, ambiente di lavoro, i notebooks, grafici, la libreria matematica, i packages standard,
il calcolo numerico e simbolico.
Testi consigliati
The Matematica Book (on line).
Modalità di valutazione
Per studenti che svolgono con profitto il corso
1 progetto da consegnare al termine del corso
difesa del progetto
Per studenti che non hanno svolto con profitto il corso o che non hanno preso parte al corso
Sviluppo di un mini progetto in aula con il matematica
LINGUAGGI DI
PROGRAMMAZIONE
Prof.ssa Margherita Napoli
3 CFU
INF/01
Obiettivi formativi
L'insegnamento si propone di fornire allo studente elementi sui modelli dei dati e gli algoritmi e l’acquisizione della
conoscenza di tecniche fondamentali di programmazione.
Contenuti del corso
1) Metodologie di programmazione. Tipi di dati astratti e modelli dati. Programmazione iterativa: cicli iterativi e
algoritmi iterativi. Invarianti di cicli. Induzione. Programmazione ricorsiva: Definizioni ricorsive, funzioni ricorsive e
prove induttive.
2) Analisi delle prestazioni di un programma:complessità temporale, passi di programma, la complessità in pratica,
notazione asintotica. Relazioni di ricorrenza e loro risoluzione. Ogni argomento nelle parti 1) e 2) è espletato anche
mediante l'applicazione a problemi esplicativi paradigmatici.
3) Il Modello dati Lista. Implementazioni di liste. Liste ordinate. Stacks e code: modelli astratti e loro implementazioni.
Realizzazione di chiamate di procedura mediante stack,
4) Il Modello dati Albero. Alberi e loro rappresentazioni. Il modello dati albero binario. Rappresentazione di alberi
binari. Attraversamento di alberi.
Testi consigliati
Aho, Ullman: Foundations of Computer Science, C Edition.
Modalità di valutazione
Gli studenti che svolgono con profitto il corso superando test di verifica e prove intercorso, devono svolgere una prova
orale.
Per studenti che non hanno svolto con profitto il corso o che non hanno preso parte al corso è prevista una prova scritta
ed una prova orale.
LOGICA MATEMATICA I
Prof. Antonio Di Nola
6 CFU
SSD MAT/01
Obiettivi formativi
Scopo di questo corso è di affrontare lo studio della logica mediante i sistemi formali.
Contenuti del corso
Algebre di Boole: Insiemi parzialmente ordinati. Reticoli. Reticoli complementati. Reticoli distributivi. Algebre di
Boole. Prime proprieta’ delle algebre di Boole. Filtri e ideali nelle algebre di Boole. Proprieta' della intersezione finita.
Ultrafiltri e loro caratterizzazioni.Teorema dell’ultrafiltro. Lemma di Tarski.
Elementi del Calcolo Preposizionale: La sintassi del calcolo preposizionale. Realizzazioni. Soddisfacibilità.
Tautologie. Un sistema di assiomi per il calcolo preposizionale. Regole di inferenza. Dimostrazioni formali. Teoremi
formali. Teorema di finitezza del calcolo preposizionale. Teorema di deduzione del calcolo preposizionale. L’algebra di
Lindenbaum del calcolo preposizionale. Teorema di completezza del calcolo preposizionale. Teorema di compattezza.
Insiemi di formule consistente. Teorema di completezza generalizzato per il calcolo preposizionale.
Elementi del Calcolo dei Predicati: Il linguaggio del calcolo dei predicati. Quantificatori. Interpretazioni delle
formule del calcolo dei predicati. Strutture relazionali. Realizzazioni e modelli di formule del calcolo dei predicati. Un
sistema di assiomi per il calcolo dei predicati. Regole di inferenza. Dimostrazioni formali. Teoremi formali. Teorema di
finitezza del calcolo dei predicati. Teorema di deduzione del calcolo dei predicati. Insiemi di formule consistente. La
consistenza del calcolo dei predicati. L’algebra di Lindenbaum del calcolo dei predicati. Completezza del calcolo dei
predicati.
Testi consigliati
Appunti dal corso.
Modalità di valutazione
Prova orale.
LOGICA MATEMATICA II
Prof. Giangiacomo Gerla
6 CFU
SSD MAT/01
Obiettivi formativi
Pervenire alla astrazione necessaria per la comprensione di aspetti “universali” delle strutture matematiche del primo
ordine (sia relazionali che algebriche). In particolare buona comprensione di quali siano le proprietà che si trasmettono
per sottostrutture, omomorfismi, isomorfismi e quali siano le proprietà che si conservano per le operazioni di quoziente,
prodotto diretto, ultraprodotto. Comprensione della “filosofia” del formalismo in matematica mostrando come sia
possibile costruire modelli di una teoria matematica in modo sintattico (teorema di completezza, costruzione del
modello di Herbrand).
Contenuti del corso
Operatori algebrici e punti uniti. Proprietà conservate dal passaggio a quoziente. Proprietà conservate dagli
omomorfismi e dalle sottostrutture. Teorema di completezza. Modelli di Herbrand. Prodotti diretti, ultraprodotti,
le classi equazionali. Proprietà che si conservano per prodotti diretti ed ultraprodotti. Applicazioni della teoria
degli ultraprodotti. Campi non archimedei. Cenni di programmazione logica (Prolog).
Testi consigliati
Appunti dal corso scaricabili da http://www.dmi.unisa.it/people/gerla/www/
- Mendelson, Introduzione alla logica matematica, Boringhieri.
- S. J. Russell, P. Norving, Intelligenza Artificiale, Ed. Prentice Hall International.
- M. L. Schagrin, W. J. Rapaport, R.R. Dipert, Logica e computer, Ed. McGraw-Hill.
- A. Asperti, A. Ciabattoni, Logica a Informatica, Ed. McGraw-Hill.
Modalità di valutazione
Esame orale usuale. Prove in laboratorio.
MATEMATICHE
6 CFU
SSD MAT/04
COMPLEMENTARI I
Prof. Franco Palladino
Obiettivi formativi
Conoscenza:
di fondamenti di matematica;
dei legami tra le principali aree della matematica;
del pensiero matematico dall’antichità ai tempi moderni.
Contenuti:
Approfondimento delle questioni fondamentali di aritmetica, algebra, geometria, trigonometria (anche per gli aspetti
astronomici) con la considerazione di algoritmi caratteristicamente correlati a questi settori.
Testi consigliati
F. Palladino, L. Lombardi, N. Palladino, “Algoritmi elementari del calcolo aritmetico e algebrico. Tradizione e
modernità”, Bologna, Pitagora Editrice.
F. Palladino, S. Sicoli, “Angoli Linee e Stelle. Origine e sviluppo della trigonometria”, Roma, ARACNE.
oltre a ulteriori numerosi testi e software: “Pascal” – “Visual basic” – “Mathematica”.
Modalità di valutazione
Prova orale.
MATEMATICHE
COMPLEMENTARI II
Prof. Giangiacomo Gerla
6 CFU
SSD MAT/04
Obiettivi formativi
• Conoscenza dei momenti fondamentali del pensiero matematico ed acquisizione critica delle nozioni base su
cui è costruita la matematica quali quelle di numero, punto, insieme.
• Capacità di percepire la matematica non come un corpo separato e definitivamente consolidato ma come uno
degli elementi fondamentali della cultura delle varie epoche e pertanto soggetto ad evoluzione ed interazione
con altri settori della cultura.
•
Essere soggetto attivo e critico nell’acquisizione della cultura matematica.
Contenuti del corso
Il corso si occupa di "filosofia della matematica" esaminando criticamente le nozioni-base della matematica ed
inquadrandole nel contesto storico di origine. In particolare: La Scuola pitagorica e sua crisi, gli Elementi di Euclide,
idealizzazione degli enti matematici, il Platonismo, Sesto Empirico. Cartesio e la crisi dell'approccio sintetico. Le
geometrie non euclidee. La teoria degli insiemi. L'aritmetizzazione della geometria e dell'analisi. Infinito attuale ed
infinito potenziale, confronto tra infiniti. Crisi della teoria degli insiemi, le antinomie. Il metodo assiomatico, il punto di
vista fondazionale e quello strutturalista.
Testi consigliati
Appunti del corso scaricabili da http://www.dmi.unisa.it/people/gerla/www/
Morris Kline, La matematica nella cultura occidentale, Feltrinelli
Bottazzini-Freguglia-Rigatelli (1992) Fonti per la storia della matematica, Sansoni
Eric T. Bell, I grandi Matematici, Sansoni, 1966
E. Agazzi, D. Palladino, Le geometrie non euclidee, Mondadori
E. Casari, La filosofia della matematica del '900, Sansoni
L. Geymonat, Storia del pensiero filosofico e scientifico, Garzanti
Rudy Rucker, La mente e l'infinito, Muzzio, 1991
Modalità di valutazione
Prova orale.
MATEMATICHE ELEMENTARI
DA UN PUNTO DI VISTA
SUPERIORE
Prof. Franco Palladino
6 CFU
SSD MAT/04
Obiettivi formativi
Il corso è finalizzato alla trattazione di questioni matematiche elementari/fondamentali mediante l’applicazione di più
avanzate e recenti nozioni matematiche. Il senso e il titolo originario del corso traggono origine da F.Klein che, nella
seconda metà dell’Ottocento, corredò il suo insegnamento a riguardo con una serie di volumi.
Contenuti del corso
I cosiddetti “Problemi classici dell’antichità”. Algoritmi numerici “storici” e applicazioni informatiche.
Modalità di valutazione
Prova orale.
METODI PER IL TRATTAMENTO
DELL’INFORMAZIONE
Prof.ssa Virginia Giorno
6 CFU
SSD INF/01
Obiettivi formativi
Il corso si prefigge in primo luogo di illustrare i concetti di base della programmazione orientata agli oggetti attraverso
lo studio del linguaggio di programmazione Java 2. In secondo luogo si intende fornire una conoscenza delle strutture
dati ponendo particolare enfasi sui collegamenti tra le strutture dati e i relativi algoritmi, includendo l’analisi della
complessità degli algoritmi considerati.
Contenuti del corso
Introduzione. Classi e oggetti. Tipi di dati fondamentali. Enunciato di decisione e di iterazione Elaborazione dei dati in
ingresso. Numeri casuali e simulazione. Progettazione di class. Pacchetti. Vettori e array.
Analisi di complessità
Liste concatenate Pile e code. Analisi di un problema: uscita da un labirinto.
Ricorsione. Backtraking. Analisi del problema delle otto regine. Alberi binari. La ricerca in un albero binario di ricerca.
Attraversamento, inserimento, eliminazione, e bilanciamento in un albero binario di ricerca.
Testi consigliati
- C.S. HORSTMANN (2002) Concetti di informatica e fondamenti di JAVA 2 (seconda edizione) Apogeo
- A. DROZDEK (2001) Algoritmi e strutture dati in JAVA Apogeo
Modalità di valutazione
Prova orale.
RICERCA OPERATIVA
Prof. Raffaele Cerulli
6 CFU
SSD MAT/09
Obiettivi formativi
Al termine del corso ci si aspetta che lo studente abbia acquisito le competenze di base per la risoluzione di problemi
reali complessi mediante l’uso di modelli matematici di programmazione lineare e di ottimizzazione su rete.
Contenuti del corso
La programmazione lineare (PL):
• Definizione di poliedri; direzioni, direzioni estreme; teorema della rappresentazione; il metodo del simplesso:
punti estremi ed ottimalità; condizioni di ottimalità e illimitatezza. L'algebra del metodo del simplesso; la
ricerca di una soluzione ammissibile di base iniziale; il metodo delle due fasi; il metoto del Big M.
Degenerazione e cicli; convergenza del metodo del simplesso.
• Utilizzo di software applicativo per la modellazione e la soluzione di problemi di programmazione lineare.
• Dualità: formulazione del problema duale; costi ridotti; teorema debole e teorema forte della dualità; gli scarti
complementari; relazioni primale-duale; interpretazione economica del duale.
• Analisi della sensitività ed analisi parametrica: analisi postottimale; variazione della soluzione ottima e del
valore ottimo di un problema di PL al variare dei dati.
Ottimizzazione su rete:
• Problemi con matrice dei vincoli totalmente unimodulare
• Cammini minimi. Massimo flusso. Trasporto. Assegnamento.
Testi consigliati
• M.S. Bazaraa, J.J Jarvis & H.D. Sherali Linear Programming and Network Flows, Second Edition, John Wiley,
1990.
• Slides ed appunti delle lezioni.
Modalità di valutazione
Due prove in itinere scritte o pratiche. Esame finale orale.
SEMIGRUPPI LIBERI E
TEORIA DEI CODICI
Prof.ssa Patrizia Longobardi
3 CFU
SSD MAT/02
Obiettivi formativi
Scopo del corso è lo studio dei semigruppi e dei monoidi liberi, con particolare riferimento a proprietà delle parole su
un alfabeto, e di elementi della teoria generale dei codici.
Contenuti del corso
Generalità sui semigruppi. Il semigruppo delle relazioni in un insieme. Sottosemigruppi (sottomonoidi), congruenze,
quozienti, omomorfismi. Semigruppi ciclici. Il semigruppo sintattico.
Il semigruppo (monoide) delle parole su un insieme. Semigruppi (monoidi) liberi. Presentazioni dei semigruppi
(monoidi). Il monoide biciclico.
Parole coniugate. Parole infinite. Le parole infinite di Thue-Morse. Parole infinite libere da quadrati. Parole di Lyndon.
Generalità sui codici.. Proprietà combinatorie dei codici. Massimalità e completezza. Famiglie di codici e di
sottomonoidi di un semigruppo libero.
Testi consigliati
J. BERSTEL ˆ D. PERRIN ˆ Theory of Codes, Academic Press, London, 1985.
J. M. HOWIE ˆ An Introduction to Semigroup Theory, Academic Press, London, 1976.
G. LALLEMENT ˆ Semigroups and Combinatorial Properties, Wiley, New York, 1979.
M. LOTHAIRE ˆ Combinatorics on Words, Addison-Wesley, Reading, 1983.
Modalità di valutazione
Prova orale.
STATISTICA MATEMATICA
Prof. Antonio Di Crescenzo
3 CFU
SSD MAT/06
Obiettivi formativi
Conoscenze di base della statistica matematica. Essere in grado di risolvere problemi che richiedono l’utilizzo degli
strumenti di base di tale disciplina.
Contenuti del corso
Campionamento e inferenza statistica
Popolazione e campione. Campione casuale. Inferenza statistica. Statistiche campionarie e loro distribuzioni.
Distribuzione campionaria di media campionaria, di varianza campionaria, di differenze di medie campionarie.
Deviazione standard campionaria. Campioni casuali tratti da popolazione normale. Distribuzione chi-quadrato.
Distribuzione di Student. Percentili superiori. Statistiche d’ordine e relative distribuzioni. Mediana campionaria. Ruolo
del teorema centrale del limite e della legge dei grandi numeri in statistica. Istogrammi e loro proprietà.
Stima puntuale e intervallare
Stimatori. Proprietà degli stimatori. Correttezza. Errore quadratico medio. Stimatori lineari corretti. Efficienza.
Efficienza relativa. Concentrazione di uno stimatore. Proprietà asintotiche. Correttezza asintotica. Consistenza. Metodo
della massima verosimiglianza. Metodo dei momenti. Stima intervallare. Intervalli fiduciari. Coefficiente di fiducia.
Metodo del cardine. Intervalli fiduciari per medie, per differenze di medie e per varianze nel caso di popolazione
normale. Intervalli fiduciari per medie di popolazioni di Bernoulli.
Verifica delle ipotesi
Ipotesi statistiche. Verifica di ipotesi. Errori di I e II tipo. Test chi-quadrato.
Regressione
Analisi di regressione. Regressione lineare semplice. Stima puntuale dei parametri di regressione. Approssimazione ai
minimi quadrati. Regressione non lineare: di tipo esponenziale e di tipo potenza. Metodo dei minimi quadrati pesati.
Testi consigliati
• Di Crescenzo A., Ricciardi L.M. (2000) Elementi di Statistica, Liguori, Napoli.
• Ross S.M. (2003) Probabilità e Statistica per l’ingegneria e le scienze. Apogeo, Milano.
Modalità di valutazione
Prova orale.
STORIA DELLE MATEMATICHE
Prof. Franco Palladino
6 CFU
SSD MAT/04
Obiettivi formativi
Conoscenza del pensiero matematico da Euclide a Leibniz e Newton.
Contenuti del corso
Euclide, “Elementi”; Bombelli, “Algebra”; Galilei, Cartesio, Fermat, Leibniz e Newton.
Testi consigliati
Ch. Boyer, “Storia della Matematica”, Milano, Mondatori.
brani delle opere originali.
Modalità di valutazione
Prova orale.
TEORIA DEI GRAFI
Prof. Francesco Bottacin
3 CFU
SSD MAT/03
Obiettivi formativi
L’obiettivo del corso è quello di presentare le idee e le tecniche principali utilizzate nello studio della teoria dei grafi e
discutere alcune delle applicazioni della teoria dei grafi a altre discipline.
Contenuti del corso
Definizioni e proprietà elementari dei grafi. Matrici associate a un grafo: matrice di adiacenza e matrice di incidenza. Il
primo teorema della teoria dei grafi. Isomorfismi e automorfismi dei grafi. Operazioni elementari sui grafi: unione,
intersezione, differenza, etc.
Sottografi, sottografi indotti e sottografi generanti. Il grado dei vertici. Grafi regolari. Il teorema di König.
Cammini e cicli in un grafo: definizioni e principali risultati. Passeggiate e percorsi in un grafo. Calcolo del numero di
passeggiate tra due vertici attraverso la matrice di adiacenza.
Grafi connessi. Le componenti di un grafo. Il teorema di Mader (senza dimostrazione).
Alberi e foreste. Caratterizzazione degli alberi. Alberi radicati. Alberi radicati normali e alberi normali generanti.
Grafi bipartiti e grafi r-partiti. Contrazioni e minori. Suddivisioni e minori topologici.
Cammini Euleriani. Il teorema di Eulero.
Altre nozioni di grafo: ipergrafi, grafi diretti (digrafi), grafi orientati, multigrafi.
Grafi planari. Grafi massimamente piani e triangolazioni piane. La formula di Eulero. Grafi planari e poliedri. I cinque
poliedri regolari.
Caratterizzazione dei grafi planari. Il teorema di Kuratowski.
Colorazioni di grafi. Colorazioni dei vertici e colorazioni dei lati di un grafo. Il numero cromatico e l'indice cromatico.
Colorazioni dei grafi planari: il teorema dei quattro colori (senza dim.), il teorema dei cinque colori. Relazioni tra il
numero cromatico e altri invarianti di un grafo. Algoritmi per la colorazione dei vertici.
Testi consigliati
R. Diestel, ''Graph Theory'', Springer-Verlag, Electronic Edition, 2000.
G. Chartrand, L. Lesniak, ''Graphs & Digraphs'', Chapman & Hall.
Modalità di valutazione
Esame orale e/o preparazione di una lezione su un argomento non trattato durante il corso.
TEORIA DEI GRUPPI
Prof.ssa Mercede Maj
6 CFU
SSD MAT/02
Obiettivi formativi
Lo scopo del corso è di illustrare classi notevoli di gruppi, presentando anche risultati recenti. Il programma può,
quindi, presentare ogni anno qualche argomento diverso.
Contenuti
Azioni di gruppi e applicazioni.
Costruzioni di gruppi.
Gruppi nilpotenti.
Gruppi risolubili.
Teoremi di spezzamento.
Gruppi con condizioni finitarie.
Testi consigliati
J. F. HUMPHREYS, A Course in Group Theory, Oxford University Press, 2000.
D.J.S. ROBINSON, An Introduction to Abstract Algebra, de Gruyter, 2004.
D.J.S. ROBINSON, A Course in the Theory of Groups, Springer Verlag, 1996.
J.S. ROSE, A Course on Group Theory, Dover, 1994.
Modalità di valutazione
Prova orale. Per gli studenti della laurea specialistica è previsto anche un seminario.
TEORIA DEI NUMERI
Prof.ssa Patrizia Longobardi
3 CFU
SSD MAT/02
Obiettivi formativi
Scopo del corso è lo studio di proprietà classiche dei numeri interi. Saranno inoltre illustrati esempi e applicazioni, e
verrà fornito qualche cenno storico.
Contenuti del corso
Richiami sulla divisibilita’ nell'insieme dei numeri naturali e dei numeri interi. Distribuzione dei numeri primi, primi di
Fermat, primi di Mersenne.
Equazioni diofantine.
Richiami sulle congruenze nell'insieme dei numeri interi. Congruenze lineari, sistemi. Il teorema di Lagrange.
Pseudoprimi e numeri di Carmichael.
Radici primitive.
Funzioni aritmetiche. Numeri perfetti.
Residui quadratici e teorema di reciprocità. Somme di quadrati. L'equazione pitagorica.
Osservazioni sull'Ultimo teorema di Fermat.
Elementi di crittografia.
Testi consigliati
G. A. JONES ˆ J. M. JONES ˆ Elementary Number Theory , Springer, 1998 (rist. 2003).
Modalità di valutazione
Prova orale.
TEORIA DELLA
COMPUTABILITA’ I
Prof. Giangiacomo Gerla
6 CFU
SSD MAT/01
Obiettivi formativi
• Conoscenza di alcune nozioni teoriche di informatica quali le macchine a registri, gli automi, la decidibilità, i
sistemi di riscrittura
• Conoscenza dei limiti teorici delle macchine calcolatrici
• Capacità di inquadrare le tecniche di programmazione in un ambito teorico generale
Contenuti del corso
Algoritmi e macchine. Macchine a memoria finita, gli automi. Cose che un automa finito non può fare (la
moltiplicazione, l’estrazione di radice). Costruire automi tramite il teorema di completezza funzionale per algebre di
Boole. Porte logiche, reti sequenziali, reti combinatorie. Macchine a memoria infinita, linguaggi di programmazione
evoluti, funzioni ricorsive, Tesi di Church. Insiemi decidibili, insiemi ricorsivamente enumerabili, macchine universali.
Cose che una macchina a memoria infinita non può fare, il teorema della fermata, il teorema di Rice. Sistemi di
riscrittura e calcolo simbolico.
Testi consigliati
Appunti dal corso scaricabili da http://www.dmi.unisa.it/people/gerla/www/
Manuale del linguaggio Mathematica
M. Minsky, Computation, finite and infinite machines, Prentice-Hall International, INC., London.
A.J. Kfoury, R.N. Moll, M.A. Arbib, Programmazione e computabilità, ETAS libri, 1986.
R. Cordeschi, La scoperta dell'artificiale, Dunod, Milano.
Y. Castelfranchi e O. Stock, "Macchine come noi", Laterza.
Modalità di valutazione
Prova orale e prove in laboratorio.
TEORIA DELL’INFORMAZIONE II
Prof.ssa Virginia Giorno
6 CFU
SSD INF/01
Obiettivi formativi
Il corso si prefigge di fornire alcune metodologie per la descrizione dell’evoluzione di sistemi dinamici. Particolare
enfasi è dedicata agli aspetti teorici presentati mediante alcune applicazioni.
Contenuti del corso
Richiami di Calcolo delle Probabilità: Funzioni generatrici e funzioni caratteristiche e loro utilizzo. Processi
stocastici: definizioni e proprietà. Esempi.
Sorgenti con memoria: Catene di Markov. Distribuzione limite e distribuzioni invarianti per catene di Markov.
Calcolo dell’entropia per catene di Markov. Sorgenti di Markov unifilari. Calcolo dell’entropia. Teorema di codifica per
sorgenti di Markov.
Modelli di crescita: Crescita malthusiana. Crescita logistica. Crescita di Gompertz. Modelli preda-predatore. Modelli
stocastici di crescita. Applicazioni a sistemi di crescita tumorale.
Modelli di attività neuronale: Potenziale di membrana e relativa rappresentazione attraverso processi di diffusione.
Modello di Wiener. Modello di Ornstein-Uhlenbeck. Il tempo di sparo come tempo di primo passaggio. Densità di
sparo.
Testi consigliati
- F. Fabris (2001) Teoria dell’Informazione, codici, cifrari. Bollati Boringhieri.
- S.M. Ross (1989) Introduction to probability models. Academic Press.
- Appunti delle lezioni.
Modalità di valutazione
Prova orale.
TEORIA DELLE FUNZIONI
Prof. Vittorio Cafagna
6 CFU
SSD MAT/05
Obiettivi formativi
Scopo del corso è familiarizzare gli studenti con le differenti classi di funzioni utilizzate in diversi rami della
matematica e discutere il paradigma dell'organizzazione dei diversi spazi funzionali secondo la teoria della
stratificazione naturale. Due esempi significativi (funzioni differenziabili secondo la struttura dei punti critici e
polinomi ortogonali secondo la struttura degli zeri) sono svolti in dettaglio.
Contenuti del corso
Revisione dei prerequisiti: algebra elementare (gruppi , anelli, spazi vettoriali), topologia generale (compattezza e
convergenze), calcolo differenziale in più variabili (determinanti Jacobiani, teorema del rango), serie (teorema di
Fourier, funzioni analitiche).
Esempio guida: stratificazione dello spazio delle matrici quadrate.
Concetto di funzione e generalizzazioni.
Spazi di funzioni e di funzioni generalizzate: aspetti algebrici e analitici. Esempi: polinomi, funzioni analitiche, serie
formali, funzioni algebriche, funzioni differenziabili, funzioni continue, funzioni misurabili, misure di Radon,
distribuzioni. Ideali e teorema degli zeri di Hilbert.
Sistemi ortogonali. Autofunzioni di problemi di Sturm-Liouville. Polinomi ortogonali. Autofunzioni dell'operatore di
Laplace-Beltrami sulle varietà riemanniane compatte. Esempi: funzioni trigonometriche in più variabili, armoniche
sferiche.
Topologie sugli spazi di funzioni. Trasversalità e genericità. Variazioni sul lemma di Sard. Funzioni di Morse. Zeri
trasversi di polinomi ortogonali.
Indici numerici: grado, numeri di intersezione, caratteristiche di Eulero, indice di Morse, numero di oscillazione di
Sturm, numero di insiemi nodali. Teorema di Courant e generalizzazioni. Congettura di Yau.
Strumentario topologico-differenziale: teorema di h-cobordismo di Smale, teorema di preparazione di WeierstrassMalgrange, teorema di pseudoisotopia di Thom, teorema di divisione di Hörmander-Malgrange-Losiacewicz.
Singolarità di mappe differenziabili. Catalogo delle catastrofi elementari.
Teoria elementare delle stratificazioni. Condizioni di Whitney e di Thom.
Applicazioni: stratificazione naturale dello spazio delle funzioni differenziabili (teoria di Thom-Mather-Cerf);
stratificazioni deboli dello spazio dei polinomi ortogonali sul cerchio unitario.
Problemi aperti e prospettive di ricerca.
Testi consigliati
Hirsch, M., Differential Topology, Springer, New York-Heidelberg-Berlin, 1976
Modalità di valutazione
Prova orale.
TOPOLOGIA
Prof.ssa Anna Di Concilio
6 CFU
SSD MAT/03
Obiettivi formativi
Il corso di Topologia tende a dare una conoscenza della Topologia ad un livello avanzato e può avere contenuti
diversificati per il suo carattere monografico.
Contenuti del corso
Teoremi di punto fisso. Omotopia e grado delle funzioni continue di sfere. Teorema di Brower. Spazi vettoriali
topologici localmente convessi. Spazi normati. Spazi di Hilbert. Cubo di Hilbert. Sostanziale differenza tra dimensione
finita ed infinita. Applicazioni di Knaster-Kuratowski-Mazurkievicz. Teoremi di Ky-Fan. Teorema di SchauderTychonoff. Teorema di Hahn-Banach-Caccioppoli. Teorema di punto fisso per spazi metrici compatti e mappe non
espansive.
Testi consigliati
J. Dugundji-A. Granas, Fixed point theory vol.I, Monografie Matematyczne PWN 1982.
N. Dunford-J.T. Schwartz, Linear operators part I : general theory, Interscience Publisher. Inc. N.Y.
R. Engelking, General Topology, PWN Polish scientific Publishers 1998.
M.Schaeffer, Topological vector spaces, Graduate Texts in Mathematics Springer-Verlag (3).
Y.A. Shashkin, Fixed points, Mathematical World vol.2 AMS 1992.
S. Willard, General Topology, Addison-Wesley Publishing Company 1976.
Modalità di valutazione
Prova orale.