Università degli Studi di Torino
DIPARTIMENTO DI FISICA
LABORATORIO I
Corso di laurea in Fisica, Anno Accademico 2007-2008
COGNOME:
NOME:
GRUPPO N.
RELAZIONE SULL’ESPERIENZA DEL 29/02/2008:
ROTAIA A CUSCINO D’ARIA
Introduzione
Lo scopo dell’esperienza è quello di verificare le leggi che regolano il moto uniforme e
uniformemente accelerato. Nel primo caso si ha una proporzionalità diretta tra gli spazi percorsi e i
tempi impiegati a percorrerli. Perciò si avrà:
∆s = v ⋅ ∆t
v = cost
(1)
Nel secondo caso poiché il corpo è soggetto a forze esterne costanti subisce un’accelerazione
anch’essa costante e si ha:
s = s0 + v0 ⋅ t +
1
a ⋅t2
2
(3)
v = v0 + a ⋅ t
(4)
Durante l’esperienza sarà utile anche la legge fondamentale che lega la forza e l’accelerazione:
F=ma
(5)
Dove F rappresenta la risultante delle forze che agiscono sul corpo.
Strumentazione
Rotaia a cuscino d’aria con asta graduata.
Carrello di forma adeguata alla rotaia e di massa Mc = (100 ± 1) g.
Una banderuola fissata sul carrello di larghezza l = (4.92 ± 0.02) mm.
Due fotocellule collegate a un computer dotato di programmi adeguati.
Un elettromagnete.
Un calibro.
Quattro pesetti di 1 grammo l’uno.
Procedimento
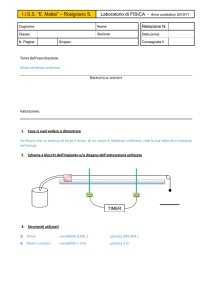
La rotaia a cuscino d’aria è un dispositivo che permette di diminuire in modo notevole gli effetti
dell’attrito. Per farlo si dispone un carrello su una rotaia metallica cava e bucherellata e attraverso
una pompa si immette nella cavità un getto d’aria che esce dai buchi posti sulla rotaia. Questo getto
diretto verticalmente verso l’alto crea una forza che tende a sollevare il carrello. Attraverso un foro
regolabile praticato nel tubo che collega la pompa alla cavità è possibile regolare il getto d’aria in
modo opportuno.
Figura 1
2
Così facendo è possibile ricreare una forza verticale che sia uguale e opposta alla forza peso; in
questo modo la reazione normale della rotaia al peso del carrello si annulla e con lei la forza di
attrito, infatti ricordiamo che:
Fatt = µ ⋅ N
Dove µ è un coefficiente che dipende dai due corpi a contatto e N è il modulo della reazione
normale della superficie su cui è appoggiato il corpo.
In realtà, come vedremo non si riesce a eliminare del tutto gli effetti della forza di attrito, tuttavia
essi risultano decisamente ridotti.
Dopo aver predisposto la rotaia nel modo appena descritto si è posto il problema di ricreare i vari
tipi di moto sempre con le stesse condizioni iniziali. Per farlo si è adottata la seguente strategia: il
carrello è stato collegato con un filo di seta a quattro pesetti, ognuno di massa 1 grammo; il filo è
stato inserito in una carrucola e i pesetti sono stati lasciati appesi a mezz’aria come mostrato in fig.
2. In questo modo i pesetti sono in grado di imprimere al corpo un’accelerazione che è possibile
stimare grazie alla seconda legge della dinamica: si scrivano le equazioni del moto dei corpi C e m
considerandoli come punti materiali e considerando il filo inestensibile e di massa trascurabile e la
carrucola ideale (I = 0):
F − M C g = 0
T = M C a
{T − mg = −ma
Sottraendo membro a membro la terza equazione dalla seconda si ha:
m ⋅ g = (m + M C ) ⋅ a
Da cui:
at =
m⋅g
m + Mc
(6)
Figura 2
3
In questo modo si è in grado di fornire al carrello un moto uniformemente accelerato. Resta il
problema di rendere tale moto uniforme. Tale problema si risolve facilmente ponendo la piattaforma
P mostrata in fig.2 sotto i pesetti. In questo modo il moto sarà accelerato fino a quando i pesetti non
raggiungono la piattaforma, dopodiché si avrà un moto rettilineo uniforme. Questo modo di operare
ci permette anche di risolvere il problema della velocità iniziale del moto. Infatti se noi facciamo in
modo che il corpo parta da fermo si avrà sempre un moto accelerato per un tratto h pari alla distanza
dei pesetti dalla piattaforma e da lì in poi un moto uniforme. Allora, combinando la (2 )e la (3) con
v0 = 0, s0 = 0 e s = h, si ha
v = 2⋅a⋅h
Siccome a e h sono quantità costanti siamo sicuri che la velocità all’inizio del moto uniforme sia
sempre la stessa. Di conseguenza se si vuole studiare il moto uniforme del carrello sarà sufficiente
utilizzare due fotocellule: la fotocellula F1, posta a distanza d > h dalla posizione di partenza e la
fotocellula F2 in un qualsiasi altro punto. In questo modo
d (F 2 F1)
= cost
∆t
Per studiare il moto uniformemente accelerato invece è sufficiente una sola fotocellula, infatti se si
toglie la piattaforma P il corpo parte da fermo e prosegue di moto uniformemente accelerato, quindi
è sufficiente rilevare il tempo trascorso dalla partenza al passaggio davanti alla fotocellula. L’ultimo
problema da risolvere, quindi è quello di sincronizzare al meglio la partenza del carrello e quella del
cronometro. L’utilizzo del computer permette di utilizzare la semplice pressione di un tasto per dare
il via al carrello e al cronometro: con l’ausilio si un elettromagnete, infatti si fa in modo che il corpo
resti fermo nell’origine e che, al momento della pressione del tasto, venga aperto il circuito che
alimenta l’elettromagnete e simultaneamente venga attivato il cronometro. In questo modo
chiaramente si ha un’ottima sincronia tra la partenza del carrello e quella del cronometro. I problemi
a livello sperimentale, tuttavia, non mancano: l’elettromagnete infatti se molto carico tende a
esercitare una forza magnetica residua anche dopo l’apertura del circuito e quindi a modificare
l’accelerazione del corpo. Per rendere minimo questo effetto si è effettuata una precisissima taratura
dell’elettromagnete rispetto al carrello in modo tale che la forza esercitata col circuito chiuso sia
appena sufficiente a mantenere il corpo fermo. Questo rende l’esperimento estremamente delicato,
infatti è sufficiente un colpo al piano di appoggio della rotaia per far partire il carrello. Dopo aver
disposto ogni cosa come descritto è il momento di effettuare le misure preliminari. Innanzitutto si
misura la massa del carrello che è stata riportata nella strumentazione. Per quanto riguarda la massa
m dei pesetti si assume che questa valga 4 grammi e non si considera la sua incertezza.
L’unico problema che si incontra nelle misure preliminari è quello delle distanze lungo la rotaia:
seppur si disponga di un’asta graduata, infatti, il suo zero non è posto nel punto di partenza del
carrello, ma in un punto leggermente più avanzato. Questo, come vedremo, non causerà problemi
per quel che riguarda il moto uniforme, ma si dovrà apportare qualche correzione per il moto
uniformemente accelerato. La misura della distanza d’ dal punto di partenza del carrello allo zero
dell’asta graduata ha causato qualche problema. Infatti per motivi di dimensioni del carrello non si è
potuto calcolare questa distanza tenendo la squadra attaccata alla rotaia, ma si è dovuto tenere circa
1 cm di distanza. Chiaramente questo tipo di misura rende molto probabile un errore di parallasse.
In ogni caso si è trovato:
d’ = (6.6 ± 0.1) cm
Nel seguito si indicherà con d’ tale distanza, con d’’i la distanza della fotocellula dallo zero dell’asta
graduata e con d’’’ un’ulteriore distanza che separa l’inizio del supporto della fotocellula e la
4
fotocellula stessa. Essa è costante e vale:
d’’’ = (9.64 ± 0.02) mm
La distanza totale della fotocellula dal punto di partenza sarà data da:
di = d’+ d’’i+ d’’’
Finora non è stato evidenziato il ruolo chiave della banderuola che viene posta sopra il carrello e fa
scattare le fotocellule al suo passaggio. Anche la larghezza di tale banderuola è una misura
preventiva che è stata effettuata con l’ausilio di un calibro e che è riportata nella strumentazione. Il
ruolo di tale misura diventerà più chiaro in seguito.
Valutazione dell’errore
Dopo aver effettuato le misure elencate sopra si è cominciato a effettuare le misurazioni dei tempi.
Le misurazioni sono essenzialmente di due tipi: misura del tempo impiegato a percorrere lo spazio
dalla partenza alla fotocellula F1 o da F1 a F2 e misura del tempo di oscuramento della banderuola.
La prima misurazione generalmente dà risultati dell’ordine del secondo, mentre la seconda ha
ordine di grandezza del centesimo di secondo e indica il tempo in cui la fotocellula viene oscurata a
causa del passaggio della banderuola B.
I primi tempi ci serviranno a valutare la dipendenza degli altri fattori del moto dal tempo stesso,
mentre gli altri, visto lo spazio estremamente ridotto, ci serviranno a valutare la velocità istantanea
nei vari punti del moto. Siccome lo strumento che ci è stato fornito ha una sensibilità di 10-5 sec
diventa problematico considerare tale sensibilità come errore su un tempo dell’ordine di 1 sec. Per
questo motivo si è deciso di effettuare una serie di 30 misure iniziali fissando la fotocellula F1 a
distanza d’’ = (12.0 ± 0.1) cm dallo zero dell’asta graduata e rilevando sia il tempo impiegato a
percorrere la distanza d = d’+ d’’+ d’’’ , sia il tempo di oscuramento della banderuola.
Siccome 30 è il limite minimo di dati per considerare notevole il campione dal punto di vista
statistico si è deciso di provare a verificare la distribuzione di probabilità di questi valori.
(t ± 0.0001)s
1.0905
1.0908
1.0984
1.0987
1.0983
1.0970
1.0981
1.0982
1.0984
1.0946
(t’±0.01)ms
1.0959
1.1002
1.0989
1.0998
1.0971
1.0939
1.0930
1.0967
1.0928
1.0953
1.0926
1.1005
1.0994
1.0954
1.0979
1.0938
1.0958
1.0960
1.0961
1.0982
16.44
16.47
16.52
16.55
16.56
16.54
16.51
16.52
16.48
16.47
16.45
16.51
16.54
16.58
16.54
16.50
16.54
16.47
16.51
16.48
16.55
16.52
16.54
16.50
16.51
16.51
16.49
16.49
16.47
16.49
5
Si ponga come ipotesi nulla che i valori non si distribuiscano secondo una distribuzione gaussiana e
si verifichi se possiamo rifiutare tale ipotesi.
Si valutano, per prima cosa, i parametri della distribuzione gaussiana:
t = 1.0964 sec
σt = 0.0027 sec
σ t = 0.0005 sec
t ' = 16.51 ms
σt’ = 0.03 ms
σ t ' = 0.01 ms
I valori riportati in Tab.1 vengono raggruppati per classi e posti in un istogramma. Nel caso di t si
costruiscono 6 classi, nel caso di t’ 7. I dettagli sono riportati negli allegati 1 e 2. Riportiamo qui
solo i grafici:
f
f
8
10
8
6
6
4
4
2
2
t'Hmsec L
tHsec L
1.092 1.094 1.096 1.098
16.44 16.46 16.48
1.102
16.52 16.54 16.56 16.58
Figura 3
Il grafico mostra che è quantomeno plausibile che la distribuzione sia di tipo gaussiano. Per
verificare in modo formale questa impressione si è eseguito in entrambi i casi il test del χ2. Per
quanto riguarda il tempo t si sono raggruppate le quattro classi agli estremi in due classi. Di
conseguenza si ha un solo grado di libertà. Fissiamo come intervallo di confidenza per il χ2 il 5% da
entrambe le parti. Allora si ha:
χ2c1= 3.84
χ2c2 = 0.004
Siccome si è ottenuto:
χ2 = 0.92
possiamo con discreta certezza rifiutare l’ipotesi nulla per quel che riguarda il tempo t.
Per il tempo t’ si avevano 2 gradi di libertà.
χ2c1= 5.99
χ2c2 = 0.103
Si è ottenuto:
χ2 = 0.87
Anche in questo caso possiamo senza dubbio rifiutare l’ipotesi nulla.
In definitiva possiamo concludere che le misure dei tempi che effettueremo nel seguito
dell’esperienza si dispongono su una distribuzione gaussiana. Diamo una formulazione definitiva
dei tempi misurati:
t = (1.0964 ± 0.0005) sec
t’= (16.51 ± 0.01) sec
6
Risultati sperimentali
L’esperimento consisteva essenzialmente di tre parti. Nelle prime due parti si analizza il moto
rettilineo uniforme e nella terza il moto uniformemente accelerato.
PARTE 1
Nella prima parte si è posta una fotocellula F1 a una distanza d fissa mentre l’altra (F2) è stata posta
in sette posizioni diverse. Si voleva verificare la dipendenza lineare tra lo spazio percorso e il tempo
impiegato a percorrerlo, quindi si è misurato il tempo impiegato per andare da una fotocellula
all’altra. In questo caso, per misurare le distanze, gli spazi d’ e d’’’ sono del tutto ininfluenti infatti
quello che ci interessa è la distanza tra le due fotocellule, cioè la differenza delle loro distanze dal
punto di partenza e quindi, se d = d’+ d’’+ d’’’ e di = d’+ di’’+d’’’, si ha:
∆d = di’’- d’’
La posizione di F1 è:
d’’= (15.4 ± 0.1) cm
Per ogni posizione di F2 si sono misurati tre tempi. Riportiamo qui i valori medi ottenuti e le
relative incertezze che, visto il numero estremamente ridotto di dati, sono state calcolate con il
metodo della semidispersione:
σt =
t max − t min
2
i
(di’’ ± 0.1) cm
(∆
∆d ± 0.1) cm
ti (sec)
1
25.2
9.8
0.3331 ± 0.0009
2
35.2
19.8
0.6702 ± 0.0005
3
45.2
29.8
1.0065 ± 0.0017
4
55.3
39.9
1.3472 ± 0.0010
5
65.3
49.9
1.6800 ± 0.0012
6
75.2
59.8
2.0234 ± 0.0034
7
85.3
69.9
2.3633 ± 0.0019
L’errore sul ∆d è stato calcolato con la formula della somma in quadratura degli errori assoluti:
σ ∆d = σ d '' 2 + σ d '' 2 = 0.14 cm
i
Tale valore è stato poi arrotondato a 0.1 cm poiché non ha senso tenere un errore con una precisione
dell’ordine di 10-2 cm su una misura con una precisione dell’ordine di 10 -1 cm. Si nota che l’errore
risultante è lo stesso che si attribuiva alle singole misure. Questo fatto si può spiegare tenendo conto
dell’indipendenza dell’errore sulle misure eseguite: in pratica è poco probabile che il valore reale
della somma di due misure con incertezza σ cada a differenza 2 σ dal valore misurato.
7
PARTE 2
Anche la seconda parte è dedicata allo studio del moto uniforme. In questo caso però si misura il
tempo di oscuramento della banderuola in vari punti della rotaia e si verifica che la velocità
istantanea resti costante. In questo caso la posizione della fotocellula sarà data da di = d’+ di’’+d’’’
e i tempi che vengono riportati, come in precedenza, sono già il valor medio di tre misure con la
relativa incertezza valutata con la semidispersione. La velocità v è stata banalmente ricavata come:
vi =
l
t 'i
Con l spessore della banderuola.
i
(di’’ ± 0.1) cm
(di ± 0.1) cm
t’i (ms)
vi (m/sec)
1
15.4
22.9
16.55 ± 0.07
0.297 ± 0.002
2
25.1
32.7
16.67 ± 0.06
0.295 ± 0.002
3
35.1
42.7
16.67 ± 0.11
0.295 ± 0.002
4
45.4
53.0
16.69 ± 0.07
0.295 ± 0.002
5
55.3
62.9
16.69 ± 0.07
0.295 ± 0.002
6
65.3
72.9
16.88 ± 0.03
0.291 ± 0.001
7
75.3
82.9
16.77 ± 0.05
0.293 ± 0.001
8
85.1
92.7
16.78 ± 0.04
0.293 ± 0.001
9
95.2
102.8
16.92 ± 0.03
0.291 ± 0.001
Per l’errore su di vale lo stesso discorso fatto in precedenza per quello su ∆d, infatti anche in questo
caso si tratta di sommare in quadratura due incertezze di 0.1 cm con un’altra il cui errore è
dell’ordine di 10-4 cm e quindi trascurabile rispetto agli altri due.
Per l’errore su v:
σ v = vi
i
σl 2
l
+
σ t' 2
i
t 'i
PARTE 3
In questa fase si devono verificare le leggi del moto uniformemente accelerato. Come fatto per il
moto uniforme effettuiamo una misura su distanze crescenti e una sui tempi di oscuramento in vari
punti della rotaia.
In questo caso non viene contata la distanza d’’’ poiché il supporto della fotocellula era girato al
contrario rispetto ai casi precedenti e la distanza tra l’inizio del supporto e la fotocellula era
decisamente trascurabile.
Si riportano allora le distanze di date da di = d’+ di’’. I tempi ti si riferiscono al tratto percorso dal
punto di partenza alla fotocellula, mentre i tempi t’i sono quelli di oscuramento rilevati alle distanze
di. In entrambi i casi, come in precedenza ogni valore deriva da tre diverse misurazioni.
Le velocità istantanee vi si sono ricavate come prima e così i relativi errori.
8
i
(di ± 0.1) cm
ti (sec)
t’i (ms)
vi (m/sec)
1
21.7
1.052 ± 0.002
12.97 ± 0.02
0.379 ± 0.003
2
31.8
1.291 ± 0.005
10.75 ± 0.01
0.458 ± 0.002
3
42.0
1.489 ± 0.003
9.28 ± 0.01
0.530 ± 0.002
4
51.7
1.666 ± 0.003
8.37 ± 0.01
0.588 ± 0.002
5
61.7
1.828 ± 0.002
7.64 ± 0.01
0.644 ± 0.003
6
71.8
1.976 ± 0.004
7.04 ± 0.01
0.699 ± 0.003
7
81.7
2.112 ± 0.003
6.64 ± 0.01
0.741 ± 0.003
Elaborazione dati
Il metodo che verrà maggiormente utilizzato in seguito per verificare che tipo di dipendenza sussiste
tra due serie di valori è quello dei minimi quadrati. Qui si riporteranno solo i risultati più
significativi mentre i calcoli in dettaglio sono svolti negli allegati. Tali calcoli essenzialmente
costituiscono la risoluzione rispetto a A e B del seguente sistema che si ricava cercando il massimo
della funzione di massima veridicità:
∑ yi = N ⋅ A + B ∑ xi
i
i
2
∑ xi ⋅ y i = A ∑ xi + B ∑ x i
i
i
i
A e B che risultano da tale sistema sono i parametri della retta y = A + B x, che è quella che meglio
approssima la dipendenza tra i nostri dati. Nel nostro caso era anche richiesto un fit parabolico. Per
farlo si utilizza un metodo che consiste a sua volta nel risolvere un sistema simile al precedente, ma
con un parametro in più da ricavare:
2
∑ y i = N ⋅ A + B∑ xi + C ∑ xi
i
i
i
2
3
∑ xi ⋅ y i =A∑ xi + B ∑ xi + C ∑ xi
i
i
i
i
x 2 ⋅ y = A x 2 + B x 3 +C x 4
∑i i ∑i i ∑i i
i
i
∑
i
(7)
La parabola che meglio approssima sarà allora: y = A + B x + C x2 .
PARTE 1
Si deve verificare la dipendenza lineare tra gli spazi ∆d e i tempi ti . Per prima cosa si è calcolato il
coefficiente di correlazione lineare:
r=
∑ (t
i
− t b )(∆d i − ∆d b )
i
∑ (t
i
i
− tb ) 2
∑ (∆d
i
− ∆d b ) 2
i
9
Dove tb e ∆db sono detti valori baricentrici e si trovano:
xb =
∑x
i
i
N
Si trova:
r = 0.999992
Come si vede tale valore è molto vicino a 1 e la p(r > r0) cioè la probabilità che i valori si
dispongano in questo modo per puro caso è praticamente nulla. Di conseguenza possiamo effettuare
un processo di regressione lineare che ci permetta di stimare i parametri della retta che meglio
approssima l’andamento dei nostri dati. Per scegliere quale grandezza porre sull’asse y e quale
sull’asse x si è effettuato un calcolo approssimato dell’errore percentuale, poiché il valore sull’asse
x viene supposto senza errore. Allora si è visto che l’errore su ∆d è circa dello 0.2%, mentre quello
su t dello 0.08%. Di conseguenza si è scelto di porre ∆d sulle ordinate e trascurare l’errore sul
tempo.
I dettagli dei calcoli sono riportati nell’allegato 3. I risultati sono:
A =(0.025 ± 0.084) cm
B = (29.59 ± 0.05) cm/sec
∆d = 0.025 + 29.59 t
∆dHcm L
1.15 = χ2c1 < χ2 = 4.71 < χ2c2 = 11.1
ν=5
70
60
50
40
30
20
10
tHsL
0.5
1
1.5
2
Dalla (1) si nota facilmente che il valore di B in realtà costituisce un’approssimazione del valore
della velocità. A invece indica il punto di partenza del moto e nel nostro caso siccome abbiamo
mantenuto una fotocellula ferma in un punto e da lì abbiamo cominciato a valutare i tempi ci
aspetteremmo un valore pari a zero. Effettuiamo allora un test di Gauss per verificare se il valore
ottenuto è compatibile con il valore zero. Il test di Gauss consiste nel confronto del valore ottenuto
con una gaussiana che abbia un massimo in corrispondenza del valore atteso. Per farlo effettuiamo
il passaggio alla variabile z della distribuzione normale standardizzata attraverso la formula:
z=
x−µ
σ
10
Nel nostro caso:
z=
0.025 − 0
= 0.30
0.084
Siccome si vuole che tale z lasci sulle code della gaussiana una probabilità maggiore del 5% allora
si dovrà avere che:
z ≤ z c = 1.96
Nel nostro caso, quindi il valore ottenuto è ampiamente compatibile col valore atteso zero.
Il valore della velocità sarà utilizzato per un confronto successivo.
PARTE 2
In questa fase bisogna verificare che la velocità si mantenga costante lungo tutta la rotaia. Per farlo
si cerca la dipendenza tra gli spazi d e le velocità istantanee v. In questo caso non calcoliamo il
coefficiente di correlazione lineare, poiché esso tende a non essere efficace quando la retta si
avvicina all’orizzontale e quindi passiamo direttamente al processo di regressione lineare. Come in
precedenza stimiamo gli errori percentuali per vedere se l’errore delle grandezze sulle ascisse è
effettivamente trascurabile. In questo caso non ci sono dubbi sulla scelta della grandezza che andrà
posta sull’asse x, infatti se si vuole ottenere una retta orizzontale si deve per forza porre d sulle
ascisse e v sulle ordinate. Si vede che l’errore su v è circa dello 0.7% e quello sulla d varia tra lo
0.1% e lo 0.6%. Di conseguenza proporzionalmente l’errore sulla d non è affatto trascurabile. In
casi come questo il procedimento standard prevede di effettuare una prima stima del coefficiente
angolare B della retta, dopodiché si proietta l’errore sulla d sull’asse delle y con la formula ricavata
dalla definizione di coefficiente angolare per cui:
σ’v = B σd
A questo punto generalmente si somma l’errore appena ricavato con σv . In questo caso, però si può
notare che, essendo la retta molto poco inclinata, il coefficiente angolare è dell’ordine di 10-3 sec-1.
Questo fa sì che σ’v sia trascurabile rispetto a σv .
I dettagli del fit si trovano sull’Allegato 4. I risultati sono:
A =(0.2973 ± 0.0015) m/sec
B = (-0.0058 ± 0.0019) sec-1
v = 0.2973 - 0.0058 d
2.17 = χ2c1 < χ2 = 6.74 < χ2c2 = 14.1
ν=7
11
m
vH L
s
0.298
0.296
0.294
0.292
dHmL
0.4
0.6
0.8
Siccome la velocità non dovrebbe dipendere dalla posizione ci si aspetterebbe un valore di B pari a
zero. Effettuando il test di Gauss si nota chiaramente che in realtà il valore ottenuto non è
compatibile con il valore atteso zero. Infatti:
z=
− 0 .0058 − 0
= − 3 .05
0 .0019
Il modulo di tale valore supera decisamente zc = 1.96. Dovremmo quindi ammettere che
l’accelerazione di attrito non sia trascurabile. Tuttavia si è scelto di adottare anche un altro tipo di
analisi dei dati: infatti combinando le equazioni (3) e (4) del moto uniformemente accelerato con d0
= 0 si ha:
2
v 2 = v 0 + 2ad
Di conseguenza risulta chiaro che per dare una stima della decelerazione media dovuta all’attrito si
debba eseguire un processo di regressione lineare tra v2 e d. Questo è stato fatto nell’allegato 5 e si è
ottenuto:
A =(0.0884 ± 0.0031) m2/sec2
B = (-0.0034 ± 0.0039) m/sec2
v2 = 0.0884 - 0.0034 d
χ2 = 0.58 < χ2c1= 2.17
ν=7
Il valore del χ2 risulta decisamente basso considerato che con χ2c1 si è indicato il valore limite
inferiore fissando un livello di confidenza del 5%. Questo ci fa pensare che sia stato sovrastimato
l’errore sulle v2 . In effetti quando si sono elevate al quadrato le velocità si è raddoppiato l’errore e
questo ha causato una notevole sovrastima, infatti le velocità, essendo numeri minori di 1, sono
diminuite, mentre gli errori sono aumentati. Allora si è deciso di effettuare il calcolo dell’errore a
posteriori sulle v2 e si è ottenuto σv2 = 0.0007.
Si è eseguito nuovamente il processo di regressione con tale valore (Allegato n. 6) e si è ottenuto:
12
A =(0.0887 ± 0.0006) m2/sec2
B = (-0.0037 ± 0.0009) m/sec2
v2 = 0.0887 - 0.0037 d
m2
v2 H L
s2
0.089
0.088
0.087
0.086
0.085
dHmL
0.4
0.6
0.8
Si nota subito che questo valore di B, al contrario di quello errato ottenuto nel primo fit tra v2 e d,
non è compatibile col valore atteso zero in accordo con ciò che si è trovato nel fit tra v e d:
z = -4.11
Di conseguenza possiamo stimare che l’accelerazione di attrito valga:
aatt = B/2 = (-0.0019 ± 0.0005) m/sec2
In questa fase possiamo confrontare anche il valore della velocità ottenuto nella prima parte
dell’esperienza con il valor medio delle velocità istantanee vi.
Per farlo si introduce una variabile aleatoria W che si ottiene come differenza tra i due valori da
confrontare. Siccome il moto uniforme, come spiegato prima, avviene sempre sotto le stesse
condizioni, le stime dei due valori dovrebbero risultare uguali, quindi il valore atteso di W è zero,
mentre la sua deviazione standard è la somma in quadratura delle incertezze sui due valori.
Posto:
v' ' =
∑v
i
N
i
σ v '' =
= 0 .2939 m / sec
v’ = (0.2959 ± 0.0005) m/sec
∑ (v
i
− v' ' ) 2
i
N
= 0 .0020 m / sec
v’’= (0.2939 ± 0.0020) m/sec
Allora:
z=
W −0
σW
=
v '− v ' '
σ v ' 2 + σ v '' 2
= − 0 .97
Concludiamo allora che i due valori della velocità sono tra loro compatibili.
13
PARTE 3
L’ultima fase dell’esperimento consisteva nella verifica delle leggi (3) e (4).
Come si vede la (3) non è una legge lineare, ma parabolica. Sarà quindi necessario risolvere il
sistema (7) per stimare la parabola che meglio rispecchia i nostri valori. Si pongono chiaramente
sull’asse delle ascisse i valori ti e sulle ordinate i valori di.
I dettagli sono riportati nell’Allegato 7. I risultati sono:
A = (0.0009 ± 0.0085) m
B = (0.0263 ± 0.0111) m/sec
C = (0.1704 ± 0.0035)m/sec2
d = 0.0009 + 0.0263 t + 0.1704 t2
0.711 = χ2c1 < χ2 = 7.91 < 9.49 = χ2c2
ν = 4.
dHmL
0.8
0.7
0.6
0.5
0.4
0.3
tHsec L
1.2
1.4
1.6
1.8
Confrontando la parabola ottenuta con la (3) si nota che nell’ipotesi di moto accelerato si avrà:
B = v0
A = d0
C = a/2
Di conseguenza, nell’ipotesi di assenza di attrito i valori attesi sarebbero:
E[B] = 0 m/sec
E[A] = 0 m
E[C] = at/2 = (0.1885 ± 0.0018) m/sec2
Dove at è l’accelerazione teorica trovata con la (6) e il suo errore è stato calcolato con la formula di
propagazione dell’errore per le misure indirette, che si riduce a:
σa
t
∂M c
=
∂at
σ MC
∂M C
m⋅ g
⋅ σ M C 2 =
=
a
σ MC =
σ
t
∂at
( M C + m)
(m + M c )2 M C
2
Prima di confrontare tali valori con quelli trovati si utilizzano le velocità istantanee per ricavare la
(4). Per prima cosa si calcola il coefficiente di correlazione lineare:
r = 0.9999
Anche in questo caso, come nel caso del moto uniforme, il coefficiente è molto vicino a 1 e la
probabilità p(r > r0) è decisamente trascurabile. Si esegue allora il processo di regressione lineare tra
le grandezze ti e le vi. Si riportano i risultati dei calcoli esplicitati nell’Allegato 8.
14
B = (0.3442 ± 0.0030) m/sec2
A =(0.0155 ± 0.0048) m/sec
v = 0.0155 + 0.3442 t
1.15 = χ2c1 < χ2 = 3.52 < χ2c = 11.1
ν = 5.
m
vH L
s
0.75
0.7
0.65
0.6
0.55
0.5
0.45
tHsec L
1.2
1.4
1.6
1.8
Questa volta la retta ottenuta va confrontata con la (4) osservando che:
A = v0
B=a
E[B] = at = (0.3769 ± 0.0036) m/sec2
E[A] = 0 m/sec
Di conseguenza si potranno effettuare 5 test di Gauss per verificare se i valori ottenuti sono in
accordo con le ipotesi:
z d0 =
zv ' =
za ' =
0.0009 − 0
= 0.11
0.0085
0.0263 − 0
= 2.37
0.0111
0.1704 − 0.1885
= −4.60
0.00182 + 0.00352
0.0155 − 0
= 3.23
zv ' ' =
0.0048
0.3442 − 0.3769
z a '' =
= −6.98
0.00362 + 0.00302
Se si confrontano i moduli di tali valori con il valore critico zc = 1.96 si trova che l’unico valore
compatibile con i valori attesi è quello di d0. I valori trovati per v0 e a sono tutti incompatibili con
quelli attesi. Di conseguenza si è costretti a rivedere le ipotesi fatte e concludere che il moto non
avvenga in assenza di attrito. Si noti che i valori trovati per velocità e accelerazione, pur non
15
essendo compatibili con i valori attesi sono tuttavia compatibili tra loro, infatti:
zv =
za =
(0.0263 − 0.0155) − 0
0.01112 + 0.00482
(0.3408 − 0.3442) − 0
0.0070 2 + 0.00302
= 0.89
= −0.44
Dati i risultati si può quindi concludere che, probabilmente, in realtà, la velocità iniziale fosse
leggermente maggiore di zero e l’accelerazione fosse minore di quella calcolata teoricamente.
Sotto l’ipotesi che la decelerazione rispetto alle previsioni teoriche sia dovuta interamente all’attrito
è possibile effettuare una stima di tale decelerazione come:
a '+ a ' '
2
Dove si è stimata l’accelerazione effettiva misurata aeff come la media delle due accelerazioni
trovate. Per stimare l’incertezza di aatt si usa ancora la formula di propagazione dell’errore:
aatt = at − aeff = at −
σa
att
∂a
= att
∂a t
2
2
2
1
1
∂a
∂a
σ at 2 + att σ a ' 2 + att σ a '' 2 = σ at 2 + σ a ' 2 + σ a '' 2
4
4
∂a ' '
∂a '
Il risultato è:
aatt = (-0.0344 ± 0.0052) m/sec2
Conclusione
Nel complesso si può notare che i risultati ottenuti sono più che soddisfacenti. Per quel che riguarda
la valutazione dell’errore possiamo ritenerci fortunati ad aver trovato una distribuzione così vicino
alla gaussiana con un numero relativamente piccolo di dati. Va anche aggiunto che gli errori stimati
in quella fase sono stati utilizzati una sola volta in seguito poiché la semidispersione in genere
superava sempre tali valori. La prima parte dell’esperienza non ha causato grossi problemi poiché i
risultati sono parsi assolutamente in linea con quello che ci saremmo aspettati. I primi problemi
sono giunti con la seconda fase dell’esperienza. In quel caso infatti si è dovuto ammettere che la
velocità non restasse costante nel moto e, di conseguenza, si è potuto stimare la decelerazione
dovuta all’attrito. Tale decelerazione è dovuta principalmente all’attrito tra il carrello e la rotaia e
alla resistenza dell’aria. La carrucola e il filo, infatti, non influiscono in nessun modo sulla
variazione della velocità dopo la fotocellula F1. Infatti, quando si studia il moto uniforme, l’attrito
tra filo e carrucola e la presenza del momento d’inerzia della carrucola diventano una sorta di errore
sistematico che influisce sulla parte di moto che noi non consideriamo (quella prima di F1) e
modifica solo la velocità iniziale del moto uniforme. Nel nostro caso si è stimata una decelerazione
complessiva di attrito che non tiene conto della dipendenza dalla velocità della resistenza dell’aria.
Riguardo le prime due parti si noti che nel test gaussiano svolto per confrontare le due velocità, si è
utilizzata la velocità media dei valori calcolati nella seconda parte e non il parametro A ottenuto dal
fit. Tale parametro infatti, non essendo la velocità uniforme, rappresentava semplicemente la
velocità iniziale del moto che è leggermente diminuita con la distanza. Si è quindi ritenuto più
significativo l’utilizzo della media dei valori misurati.
La terza parte dell’esperienza è stata senza dubbio la più problematica. I valori ottenuti, infatti non
rispecchiavano in alcun modo quelli trovati per via teorica. In più, se è semplice spiegare un valore
dell’accelerazione inferiore alle attese, non è altrettanto semplice spiegare il valore della velocità
16
iniziale superiore a zero. Le ipotesi più probabili sono che vi fosse un lieve divario tra la partenza
del cronometro e il rilascio del carrello, che il moto risentisse in qualche modo dell’effetto
dell’elettromagnete oppure che si sia commesso un qualche errore sistematico nella misurazione
degli spazi. Nel primo caso si noti che non ci si sarebbe potuti accorgere in alcun modo di tale
errore nello studio del moto uniforme poiché i tempi erano misurati tra due fotocellule e non dal
punto di partenza.
Come detto, invece, il discorso è più semplice per quel che riguarda l’accelerazione: essa, infatti,
risente chiaramente delle forze di attrito. In questo caso, inoltre, ci si può aspettare che la
decelerazione di attrito sia maggiore di quella trovata nella seconda parte. Su tale moto, infatti,
influiscono anche il momento d’inerzia della carrucola e l’attrito tra filo e carrucola. Si può allora
verificare che l’accelerazione stimata nella seconda parte sia effettivamente inferiore a quella
stimata nella prima. Poniamo allora come ipotesi nulla che aatt1 ≥ aatt2 e verifichiamo che sia
possibile rifiutare tale ipotesi. Per farlo si introduce una nuova variabile W:
W = a att 2 − a att1
Se si può rifiutare l’ipotesi nulla deve risultare W > 0. Allora si può effettuare un test di Gauss con
valore atteso zero e porre che la probabilità che W sia uguale a zero sia minore del 5%. Il test, però,
in questo caso verrà effettuato a una coda sola, poiché si vuole considerare solo l’eventualità che il
valore di W sia maggiore di zero. Allora in questo caso il valore critico sarà zc = 1.65.
zc =
(a att 2 − aatt1 ) − 0
σa
2
att 1
+ σ aatt 2
2
=
0.0344 − 0.0019
0.0003 2 + 0.0052 2
= 6.23 > zc
Si può quindi senza dubbio rifiutare l’ipotesi nulla e ammettere che l’attrito nel caso del moto
uniformemente accelerato sia maggiore di quello nel moto rettilineo uniforme.
17