esercizio svolto

modulo B2
ESERCIZIO
1
Unità 4 La flessione composta
Il cemento armato: metodo agli stati limite
S V O LTO
La flessione composta: sforzo normale e flessione retta
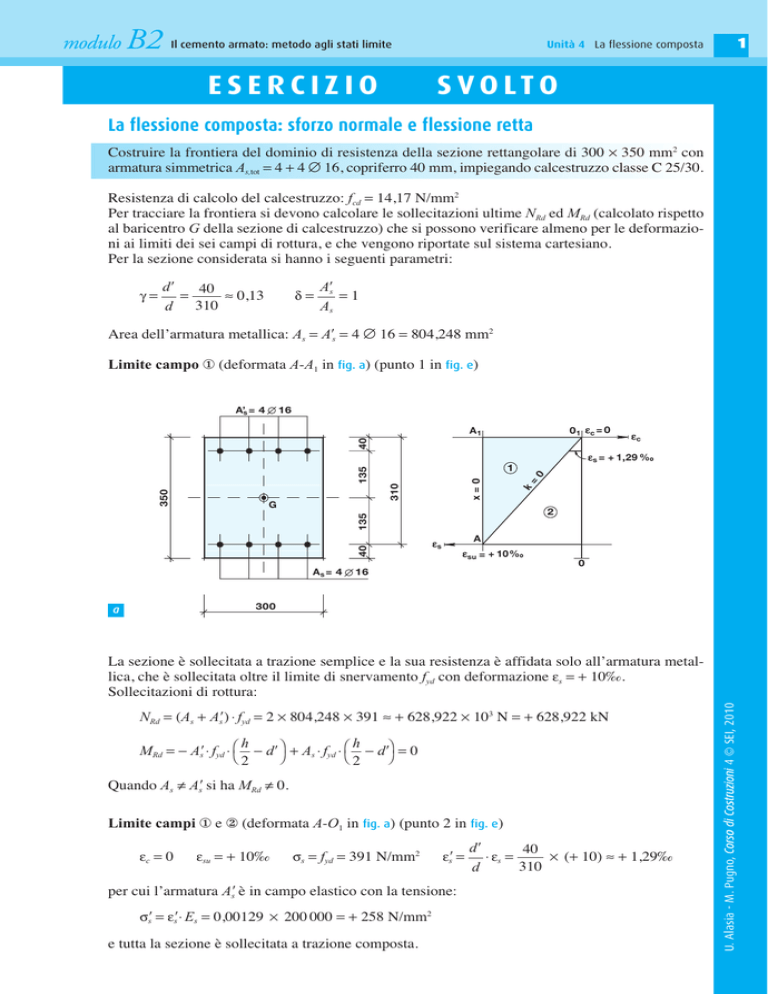
Costruire la frontiera del dominio di resistenza della sezione rettangolare di 300 × 350 mm2 con
armatura simmetrica As,tot = 4 + 4 ∅ 16, copriferro 40 mm, impiegando calcestruzzo classe C 25/30.
Resistenza di calcolo del calcestruzzo: fcd = 14,17 N/mm2
Per tracciare la frontiera si devono calcolare le sollecitazioni ultime NRd ed MRd (calcolato rispetto
al baricentro G della sezione di calcestruzzo) che si possono verificare almeno per le deformazioni ai limiti dei sei campi di rottura, e che vengono riportate sul sistema cartesiano.
Per la sezione considerata si hanno i seguenti parametri:
γ=
d⬘
40
=
≈ 0,13
d 310
δ=
A⬘s
=1
As
Area dell’armatura metallica: As = A⬘s = 4 ∅ 16 = 804,248 mm2
Limite campo ① (deformata A-A1 in fig. a) (punto 1 in fig. e)
A’s = 4
16
01 ec = 0
40
A1
ec
135
2
A
es
40
As = 4
=
0
G
k
x=0
310
350
135
e s = + 1,29 %
1
e su = + 10 %
0
16
300
a
NRd = (As + A⬘s ) ⋅ fyd = 2 × 804,248 × 391 ≈ + 628,922 × 103 N = + 628,922 kN
MRd = − A⬘s ⋅ fyd ⋅ ⎛
h
⎝2
− d⬘⎞ + As ⋅ fyd ⋅ ⎛
⎠
h
⎝2
− d⬘⎞ = 0
⎠
Quando As ≠ A⬘s si ha MRd ≠ 0.
Limite campi ① e ② (deformata A-O1 in fig. a) (punto 2 in fig. e)
εc = 0
εsu = + 10‰
σs = fyd = 391 N/mm2
ε⬘s =
per cui l’armatura A⬘s è in campo elastico con la tensione:
σ⬘s = ε⬘s ⋅ Es = 0,00129 × 200 000 = + 258 N/mm2
e tutta la sezione è sollecitata a trazione composta.
d⬘
40
⋅ εs =
× (+ 10) ≈ + 1,29‰
310
d
U. Alasia - M. Pugno, Corso di Costruzioni 4 © SEI, 2010
La sezione è sollecitata a trazione semplice e la sua resistenza è affidata solo all’armatura metallica, che è sollecitata oltre il limite di snervamento fyd con deformazione εs = + 10‰.
Sollecitazioni di rottura:
modulo B2
2
Unità 4 La flessione composta
Il cemento armato: metodo agli stati limite
Sollecitazioni di rottura:
NRd = A⬘s ⋅ σ⬘s + As ⋅ fyd = 804,248 × 248 + 804,248 × 391 ≈ + 521,957 × 103 N =
= + 521,957 kN
MRd = (As ⋅ σs − A⬘s ⋅ σ⬘s ) ⋅ ⎛
h
⎝2
− d⬘⎞ = (804,248 × 391 − 804,248 × 258) × ⎛
⎠
350
⎝ 2
− 40⎞ ≈
⎠
≈ + 14,44 × 10 N mm = + 14,44 kN m
6
Campo ② (deformata A-A⬘ in fig. b) (punto 3 in fig. fig. e)
εsu = + 10‰
310
350
A’
F
B
ec
k=
0
135
2
59 67
0,2
0,1
k=
k=
3
A
es
40
01
2a
G
As = 4
es, = 0
,
40
135
1
29
-3,5 %
0,1
k=
16
x= d
A’s = 4
x = d⬘
-2 %
σ⬘s = 0
d⬘
40
⋅ εsu = −
× (+ 10‰) ≈ − 1,48‰
310 − 40
d − d⬘
51,67
σs = fyd
εc = −
80,37
ε⬘s = 0
esu = + 10%
0
16
300
b
L’asse neutro passa per il baricentro dell’armatura A⬘s.
Sollecitazioni di rottura:
NRd = − fcd ⋅ 0,8 ⋅ x ⋅ b − A⬘s ⋅ σ⬘s + As ⋅ fyd = − 14,17 × 0,8 × 40 × 300 − 804,248 × 391 ≈
≈ + 178,429 × 103 N = + 178,429 kN
h
⎝2
− 0,4 ⋅ x⎞ + A⬘s ⋅ σ⬘s ⋅ ⎛
⎠
= ⎡⎢14,17 × 0,8 × 40 × 300 × ⎛
350
⎝ 2
⎣
h
⎝2
− d⬘⎞ + As ⋅ fyd ⋅ ⎛
⎠
⎠⎦
⎣
≈ + 64,08 × 10 N mm = + 64,08 kN m
La sezione è parzializzata.
εc = − 2‰
x=
ε⬘s =
εc
εc − εsu
2a
(deformata A-F in fig. b) (punto 4 in fig. e)
εs = + 10‰
⋅d −
− d⬘⎞ =
⎠
− 0,40 × 40⎞ ⎤⎥ + ⎡⎢804,248 × 391 × ⎛
6
Limite campo
h
⎝2
σs = fyd = 391 N/mm2
−2
× 310 ≈ 51,67 mm
− 2 − 10
51,67 − 40
x − d⬘
⋅ εc =
⋅ (− 2) ≈ − 0,452‰
51,67
x
L’armatura compressa è in campo elastico e quindi:
σ⬘s = ε⬘s ⋅ Es = − 0,000452 × 200 000 = − 90,40 N/mm2
350
⎝ 2
− 40⎞ ⎤⎥ ≈
⎠⎦
U. Alasia - M. Pugno, Corso di Costruzioni 4 © SEI, 2010
MRd = + fcd ⋅ x ⋅ b ⋅ ⎛
modulo B2
3
Unità 4 La flessione composta
Il cemento armato: metodo agli stati limite
Sollecitazioni di rottura:
NRd = − fcd ⋅ 0,8 ⋅ x ⋅ b − A⬘s ⋅ σ⬘s + As ⋅ fyd =
= − (14,17 × 0,8 × 51,67 × 300) − (804,248 × 90,40) + (804,248 × 391) ≈
≈ + 66,038 × 103 N = + 66,038 kN
MRd = ⎡⎢+ fcd ⋅ 0,8 ⋅ x ⋅ b ⋅ ⎛
h
⎝2
⎣
− 0,4 ⋅ x⎞ ⎤⎥ + A⬘s ⋅ σ⬘s ⋅ ⎛
= ⎡⎢14,17 × 0,8 × 51,67 × 300 × ⎛
350
⎝ 2
⎣
+ 804,248 × 391 × ⎛
350
⎝ 2
h
⎝2
⎠⎦
− d⬘⎞ + As ⋅ fyd ⋅ ⎛
⎠
h
⎝2
− d⬘⎞ =
⎠
− 0,4 × 51,67⎞ ⎤⎥ + 804,248 × 90,40 × ⎛
350
⎝ 2
⎠⎦
− 40⎞ +
⎠
− 40⎞ ≈ + 79,386 × 106 N mm = + 79,386 kN m
⎠
Limite campi ② e ③ (deformata A-B in fig. b) (punto 5 in fig. e)
εc = − 3,5‰
x=
εs = + 10‰
σs = fyd = 391 N/mm2
− 3,5
× 310 ≈ 80,37 mm
− 3,5 − 10
ε⬘s =
80,37 − 40
× (−3,5) ≈ − 1,758‰
80,37
L’armatura compressa è ancora in fase elastica con la tensione:
σ⬘s = ε⬘s ⋅ Es = − 0,001758 × 200 000 = − 351,60 N/mm2
Sollecitazioni di rottura:
NRd = − (14,17 × 0,8 × 80,37 × 300) − (804,248 × 351,60) + (804,248 × 391) =
= − 241,635 × 106 N mm = − 241,635 kN
MRd = + [14,17 × 0,8 × 80,37 × 300 × (175 − 0,4 × 80,37)] + [804,248 × 351,60 ×
× (175 − 40)] + 804,248 × 391 × (175 − 40) ≈ + 119,67 × 106 N mm = + 119,67 kN m
Limite campi ③ e ④ (deformata D-B in fig. c) (punto 6 in fig. e)
εc = − 3,5‰
εs = εyd = + 1,955‰
A’s = 4
16
-2 %
-3,5 %
40
01
e’s
3
k=
G
40
135
4
es
D
e yd = + 1,955 %
E
0
As = 4
c
16
300
x=
− 3,5
× 310 ≈ 198,90 mm
− 3,5 − 1,955
ε⬘s =
198,90 − 40
x − d⬘
⋅ εc =
× (− 3,5) ≈ − 2,796‰ > εyd
198,90
x
ec
0,6
42
k
=
1
5
U. Alasia - M. Pugno, Corso di Costruzioni 4 © SEI, 2010
350
310
135
198,90
B
modulo B2
4
Unità 4 La flessione composta
Il cemento armato: metodo agli stati limite
L’armatura compressa A⬘s è snervata per cui σs = σ⬘s = fyd.
Sollecitazioni di rottura:
NRd = − fcd ⋅ 0,8 ⋅ x ⋅ b + (As − A⬘s ) ⋅ fyd = − 14,17 × 0,8 × 198,90 × 300 ≈
≈ − 676,42 × 103 N = − 676,42 kN
MRd = + ⎡⎢fcd ⋅ 0,8 ⋅ x ⋅ b ⋅ ⎛
h
⎝2
⎣
− 0,4 ⋅ x⎞⎤⎥ + A⬘s ⋅ fyd ⋅ ⎛
h
⎝2
⎠⎦
− d⬘⎞ + As ⋅ fyd ⋅ ⎛
⎠
− d⬘⎞ =
h
⎝2
⎠
= + 14,17 × 0,8 × 198,90 × 300 × (175 − 0,4 × 198,90) + 2 × 804,248 × 391 × (175 − 40) ≈
≈ + 149,462 × 106 N mm = + 149,462 kN m
Limite campi ④ e ⑤ (deformata E-B in fig. d) (punto 7 in fig. e)
εs = 0
εc = − 3,5‰
A’s = 4
x = d = 310 mm
16
-2 %
01
-3,5 %
40
F
B
ec
350
310
4
x
40
135
G
As = 4
es
E
es
=
d
5
=
h
6
0
16
x
200
135
e’s
F1
300
d
ε⬘s =
310 − 40
d − d⬘
⋅ εc =
× (− 3,5) = −3,048 N/mm2 > εyd
310
d
per cui l’armatura compressa è snervata e quindi: σ⬘s = − fyd = − 391 N/mm2 e σs = 0.
Sollecitazioni di rottura:
≈ − 1368,709 × 103 N = − 1368,709 kN
MRd = + ⎡⎢fcd ⋅ 0,8 ⋅ x ⋅ b ⋅ ⎛
⎣
h
⎝2
− 0,4 ⋅ x⎞⎤⎥ + A⬘s ⋅ fyd ⋅ ⎛
⎠⎦
h
⎝2
− d⬘⎞ =
⎠
= + [14,17 × 0,8 × 310 × 300 × (175 − 0,4 × 310)] + 804,248 × 391 × (175 − 40) ≈
≈ + 96,219 × 106 N mm = + 96,219 kN m
Limite campi ⑤ e ⑥ (deformata O-B in fig. d ) (punto 8 in fig. e)
εc,sup = − 3,5‰
εc,inf = 0
x = h = 350 mm
εs =
40
d⬘
⋅ εc,sup =
× (− 3,5) = − 0,4‰ < εyd
350
h
ε⬘s =
350 − 40
h − d⬘
⋅ εc,sup =
× (− 3,5) = − 3,1‰
350
h
σs = εs ⋅ Es = − 0,0004 × 200 000 = − 80 N/mm2
σ⬘s = − 391 N/mm2
U. Alasia - M. Pugno, Corso di Costruzioni 4 © SEI, 2010
NRd = − fcd ⋅ 0,8 ⋅ x ⋅ b − A⬘s ⋅ fyd = − 14,17 × 0,8 × 310 × 300 − 804,248 × 391 ≈
modulo B2
5
Unità 4 La flessione composta
Il cemento armato: metodo agli stati limite
Sollecitazioni di rottura:
NRd = (− 14,17 × 0,8 × 350 × 300) − (804,248 × 391) − 804,248 × 80 ≈
≈ − 1569,08 × 103 N = − 1569,08 kN
MRd = + [14,17 × 0,8 × 350 × 300 × (175 − 0,4 × 350)] + 804,248 × 391 × (175 − 40) +
− 804,248 × 80 × (175 − 40) ≈ + 75,426 × 106 N mm = + 75,426 kN m
Limite campo ⑥ (deformata F-F1 in fig. d ) (punto 9 in fig. e)
εc,sup = εc,inf = − 2‰;
εs = ε⬘s = − 2‰;
x = ⬁;
σs = σ⬘s = − fyd = − 391 N/mm2
Il calcestruzzo è uniformemente compresso.
NRd = − fcd ⋅ b ⋅ h − (As − A⬘s ) ⋅ fyd = − (14,17 × 300 × 350) − (2 × 804,248 × 391) ≈
≈ − 2116,77 × 103 N = − 2116,77 kN
MRd = ( fcd ⋅ b ⋅ h ⋅ 0) + (As − A⬘s ) ⋅ ⎛
h
⎝2
− d⬘⎞ = (14,17 × 300 × 350 × 0) + (804,248 − 804,248) ×
⎠
× (175 − 40) = 0
La sezione è soggetta a compressione semplice.
I risultati sono riepilogati nella tabella 1.
Tabella 1
k
NRd (kN)
MRd (kN m)
A-A1
A-O1
A-A⬘
A-F
A-B
D-B
E-B
O-B
F-F1
-ⴥ
0
0,129
0,167
0,259
0,642
1
1,129
+ⴥ
+ 628,922
+ 521,957
+ 178,429
+ 66,038
- 241,635
- 676,420
- 1368,709
- 1569,080
- 2116,770
0
+ 14,440
+ 64,080
+ 79,386
+ 119,670
+ 149,462
+ 96,219
+ 75,426
0
+ MRd
Riportando i valori su un sistema
cartesiano si ottiene il dominio di
resistenza della sezione rappresentata in figura e.
Questo esercizio svolto ha consentito di illustrare il criterio che consente di tracciare il dominio di resistenza di una sezione; risulta evidente
che il procedimento manuale è
molto laborioso, per cui è praticamente indispensabile disporre di un
idoneo programma di calcolo.
6
5
7
4
8
3
+ NRd
e
2
1
9
- M Rd
- NRd
U. Alasia - M. Pugno, Corso di Costruzioni 4 © SEI, 2010
Deformata