ESERCIZI SUL MOTO RETTILINEO UNIFORME
12-11-00
1 - Un'auto percorre 40 m in 4 s e altri 24 m in 6 s. Quale 6 stata la velocità media nei due tratti e quella sull'intero
percorso ?
Velocità media nel primo tratto (v 1m)
∆s1 40m
=
= 10 m / s
∆t 2
4s
v1m =
Velocità media nel secondo tratto (v 2m)
v2 m =
∆s 2 24m
=
=4m/s
∆t 2
6s
Velocità media sull'intero percorso (v m)
vm =
∆s tot 40m + 24m 64 s
=
=
= 6.4 m / s
∆t tot
4s + 6s
10 s
La velocità può anche essere calcolata come media pesata (con pesi uguale ai tempi di percorrenza)
delle velocità medie dei singoli tratti:
vm =
∆t1 ⋅ v1m + ∆t 2 ⋅ v 2 m 4 s ⋅ 10m / s + 6 s ⋅ 4m / s 40m + 24m
=
=
= 6.4 m / s
∆t1 + ∆t 2
4s + 6s
10s
2 - Una vettura percorre 15 km divisi in due tratti.
II primo tratto, lungo 5 km, viene percorso in 3 minuti e 20 secondi; il secondo tratto viene percorso alla media di 60
km/h. Qual è la velocità media complessiva di tutto il percorso ?
Calcolo il tempo di percorrenza del secondo tratto
∆t 2 =
∆s 2 15km − 5km 10km ⋅ h
=
=
= 0.1 6 h
v2
60km / h
60km
Trasformo il tempo di percorrenza del primo tratto in ore
∆t1 = 3 min 20s = 180s + 20s = 200s =
200
h = 0.0 5 h
3600
La velocità media (vm) sull'intero percorso vale:
vm =
15km
15km
15km ⋅ 3600
=
=
= 67.5 km / h
10
200
600 + 200
800h
h+
h
h
60
3600
3600
N.B: quando si lavora con numeri periodici, è sempre meglio utilizzare la loro espressione frazionaria originale. In
questo modo si evita di introdurre gli errori dovuti al troncamento
3 - Un treno passa per la stazione A alle ore 8 e 10' e, viaggiando con moto uniforme, passa per la successiva
stazione B, che dista 12 km da A, alle ore 8 e 15'. Continuando a mantenere sempre la stessa velocità, a che ora
passerà per la stazione C, che dista 15 km da B ?
Quale sarà la sua distanza da A alle ore 8 e30' ?
Calcolo la velocità media ( vAbm) nel primo tratto (da A a B)
v ABm =
∆s AB 12km 12km
=
=
= 48 km / h
∆t AB
15'
0.25h
Calcolo il tempo impiegato per raggiungere la stazione C partendo da B
∆ BC =
15km
15
15
=
h=
⋅ 3600s = 1125s = 18 min 45s
48km / h 48
48
Calcolo l'ora in cui il treno passerà per C
t = 8h 15 min( ora di arrivo a B) + 18 min 45s (tempo impiegato per percorre il tratto BC) = 8h 33min 45s
Calcolo la distanza da A alle ore 8 e 30 min
Alle ore 8 e 15 min il treno dista da A 12 km. Devo pertanto calcolare lo spazio percorso nei successivi 15 min
sapendo che la velocità media è 48 km/h
15 min -> un quarto d'ora
in un'ora 48 km -> in un quarto d'ora 12 km
La distanza cercata è allora pari a : 12 km +12 km = 24 km
4 - Dopo l'apertura del paracadute, un paracadutista cade con una velocità pressoché uniforme di 12 m/s. Quanto
tempo impiega a cadere di 228 m ? Se, dopo di ciò, continua a cadere per altri 25 s, quant'è il dislivello
complessivo percorso ?
Calcolo il tempo ∆t1 impiegato a percorrere 228 m
∆t1 =
∆s1 228m
=
= 19 s
v
12m / s
Calcolo lo spazio percorso nei successivi 25 s
∆s 2 = v m ⋅ ∆t 2 = 12m / s ⋅ 25s = 300 m
Il dislivello complessivo ∆s percorso vale:
∆s = ∆s1 + ∆s 2 = 228m + 300m = 528m
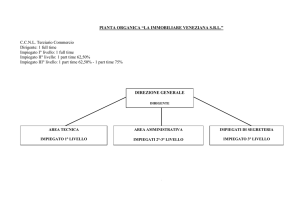
5 - Rappresentare su un unico grafico (s-t) i moti dei due oggetti seguenti e calcolare in che istante si incontrano:
• All'istante t = 0 , l'oggetto A si trova al km 0 e viaggia con moto rettilineo uniforme pari a 60 km/h per 2 ore, poi a
300 km/h per 1 ora, infine a 70 km/h per 3 ore.
• L'oggetto B è fermo al km 300.
700
600
A
Spazio (km)
500
400
300
B
200
100
0
0
1
2
3
4
5
6
Tempo (h)
∆t2
∆t1
∆t
Determino il tempo in corrispondenza del quale avviene l'incontro, ovvero il tempo impiegato dall'oggetto A a
compiere uno spazio pari a 300 km
•
dopo 2 h il corpo A ha compiuto già uno spazio di 120 km
∆t1 = 2h
•
dobbiamo determinare il tempo impiegato dal corpo A a compiere i restanti 180 km (alla velocità costante
di 300 km/h)
∆t 2 =
∆s 2 180km
=
⋅ h = 0.6h
v2
300km
I due corpi si incontrano dopo 2.6 h ovvero dopo 2h e 36 minuti dall'inizio del periodo di osservazione
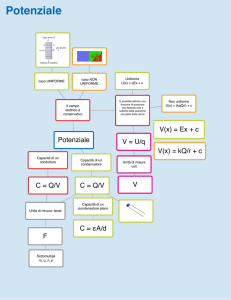
6 - Rappresentare su un unico grafico (s-t) i moti dei due oggetti seguenti e calcolare in che istante si incontrano:
• L'oggetto A è fermo al km 240 per mezz'ora; in seguito torna indietro, con moto uniforme, per 2 ore alla
velocità di 120 km/h.
• L'oggetto B A femo al km 100.
240
A
220
200
Spazio (km)
180
160
140
120
100
B
80
60
40
20
0
0.0
0.5
1.0
1.5
2.0
2.5
Tempo (h)
∆t2
∆t1
∆t
Calcolo il tempo in corrispondenza del quale avviene l'incontro dei due oggetti, ovvero il tempo impiegato dall'oggetto
A a raggiungere il km 100
•
Dopo 0.5 h l'oggetto A si trova al km 240
∆t1 = 0.5h = 30 min
•
Devo ora calcolare il tempo impiegato per compiere, a ritroso, 140 km alla velocità di 120 km/h
∆t 2 =
∆s 2 140km
140
7
1
=
⋅h =
⋅ h = ⋅ h = 1 + ⋅ h = 1h 10 min
v2
120km
120
6
6
L'incontro dei due oggetti avverrà dopo 1 h e 40 min dall'inizio del periodo di osservazione
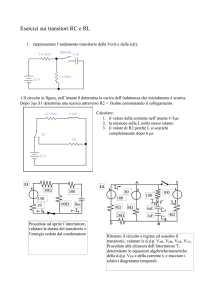
7 - Rappresentare su un unico grafico (s-t) i moti dei due oggetti seguenti e calcolare in che istante si incontrano:
• All'istante t = 0 , I'oggetto A si trova al km 350, poi torna indietro per un'ora e mezza, con moto rettilineo
uniforme, alla velocità di i 00 km/h , in seguito rimane fermo per 1 ora.
• L'oggetto B è fermo al km 250.
350
300
A
Spazio (km)
250
B
200
150
100
50
0
0.0
0.5
1.0
1.5
2.0
2.5
Tempo (h)
∆t1
Calcoliamo il tempo in cui avviene l'incontro dei due oggetti, ovvero il tempo impiegato dal corpo A per compiere, a
ritroso 100 km (350 - 250) alla velocità di 100 km/h
Il tempo richiesto è esattamente un'ora