CORSO DI COSTRUZIONI IN ACCIAIO 270 Laurea Magistrale I

CORSO DI COSTRUZIONI
IN ACCIAIO
270 Laurea Magistrale
I anno – I semestre
ESERCITAZIONE:
CALCOLO DELLA STRUTTURA DI UN CAPANNONE
INDUSTRIALE SITO NELLA CITTÀ DI CAGLIARI
Parte 1
TITOLARE: Prof. Ing. Barbara De Nicolo
RELATORE: Ing. Daniel Meloni
PREMESSA
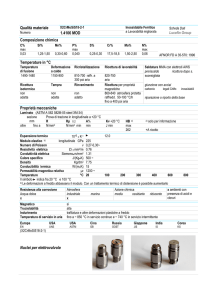
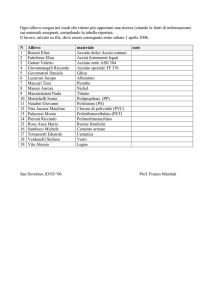
Nel seguito verrà sviluppata la verifica strutturale della struttura in acciaio di
un capannone industriale. L’esercitazione è liberamente ispirata ad un edificio
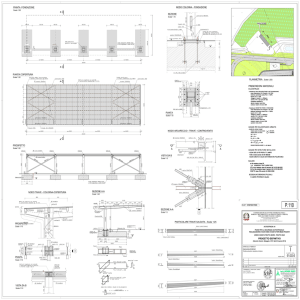
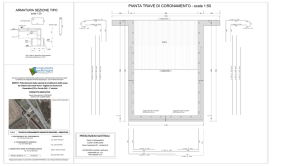
esistente di cui si riportano in seguito alcune immagini e gli elaborati grafici. Le
verifiche strutturali verranno effettuate in osservanza delle indicazioni del D.M.
14/01/2008 e dell’Eurocodice 3.
DESCRIZIONE DELLA STRUTTURA
La struttura in esame è un tipico capannone industriale monopiano a struttura
in acciaio, con una pianta rettangolare di dimensioni 88x92 m ed un’altezza
massima di circa 9.00 m, con un corpo centrale principale di dimensioni 72x92
m e due corpi laterali di altezza inferiore (circa 5.30 m).
1
La struttura portante del corpo centrale è regolare con pilastri HEA240 disposti
a maglia regolare 24x12 m, in numero quindi di 4x9, con un’altezza dalla
pavimentazione all’imposta delle travi di copertura di 6.50 m.
I pilastri sostengono un sistema di travi principali disposte trasversalmente con
luce di 24.00 m ed interasse 12.00 m, con schema di semplice appoggio. Si
tratta di travi reticolari del tipo “Pratt” di altezza 2.40 m.
2
Le sezioni della struttura esistente prevedono per la briglia superiore e
inferiore un doppio UPN120 e montanti ad interasse di 2.00 m realizzati con un
doppio UPN80, saldati talvolta sull’anima, talvolta sulle ali.
Le diagonali sono costituite da piatti a sezione piena 80x25 o 80x40 mm.
Sulle travi principali sono impostate le travi secondarie di tipo “Vierendeel” in
semplice appoggio su luci di 12.00 m, interasse di 4.00 m (ogni 2 campi della
trave principale) e altezza di 0.60 m.
Le briglie inferiori e superiori sono costituite da profili a T100x100, i montanti
ad interasse 0.50 m sono costituiti da un doppio angolare a lati uguali L40x4
saldati all’anima dei correnti.
Entrambe le due tipologie di travi sono assemblate per saldatura, mentre la
connessione mutua è ottenuta per bullonatura.
Al di sopra di questo sistema di travi è collocata una copertura a shed
costituita come segue: al di sopra delle travi secondarie, quindi con scansione
ogni 4.00 m, sono imbullonati un montante alto circa 1.80 m e una diagonale
di lunghezza circa 4.40 m, realizzati con profili IPE160, mutuamente saldati
all’apice.
3
Sopra il diagonale sono appoggiati gli arcarecci ad interasse medio di 0.86 m,
ottenuti saldando due profili a C alti 80 mm.
A loro volta gli arcarecci sostengono dei pannelli sandwich coibentati con cui è
realizzato l’impalcato di copertura. Il pannello verticale dello shed è realizzato
con un infisso leggero in alluminio.
Le porzioni laterali più basse dell’edificio sono costituite, per quanto riguarda la
copertura, da elementi inclinati impostati da un lato ad una travatura di bordo
del tipo Vierendeel, longitudinale rispetto alla pianta dell’edificio, dall’altra su
pilastri perimetrali ottenuti con IPE140 a scansione ogni 4.00 m.
Il capannone è suddiviso tramite partizioni interne leggere in lamiera grecata
ed è chiuso perimetralmente da una tamponatura in mattoni pieni fino ad un
altezza di circa 2.50 m, quindi da infissi e pannelli prefabbricati in lamiera
grecata, ed è suddivisa in campi dai pilastri perimetrali summenzionati.
IL DIMENSIONAMENTO DESCRITTO È BASATO SU UN PROGETTO DEGLI
ANNI ’60. NEL PROSEGUO APPLICHEREMO GLI STANDARD PREVISTI
DALLE ATTUALI NORMATIVE E SE NECESSARIO RIPROGETTEREMO GLI
ELEMENTI STRUTTURALI NON ADEGUATI.
Seguono alcune immagini della struttura esistente.
4
5
6
7
8
9
Nel proseguo si farà riferimento alle seguenti norme nazionali:
− D.M. 14/01/2008: Norme tecniche per le costruzioni. Pubblicate
sulla G.U. del 4/02/2008 n.22;
− Circ. del CCSLLPP 02/02/2009 n.617: Istruzioni per l’applicazione
delle Norme Tecniche per le costruzioni di cui al D.M.
14/01/2008;
e al Metodo degli Stati Limite.
VITA NOMINALE
Dalla tabella 2.4.I
L’edificio in questione è un’opera ordinaria e pertanto si assumerà
VN=50 anni.
Si considererà inoltre una classe d’uso II, per edifici oggetto di
normali affollamenti.
Questi parametri sono significativi per la determinazione del
periodo di riferimento VR delle azioni naturali, soprattutto quella
sismica.
MATERIALI
Ipotizzeremo l’uso di profilati laminati a caldo realizzati con acciaio
duttile di grado S235JR conforme alla norma armonizzata UNI EN
10025 (ex Fe360B). Tale materiale è caratterizzato dalle seguenti
proprietà meccaniche:
peso specifico = 78.5 KN/m3
modulo di elasticità = 210000 MPa
modulo di poisson = 0.30
modulo di elasticità tangenziale = 80769 MPa
carico unitario di rottura ftk = 360 MPa
carico unitario di snervamento fyk = 235 MPa
10
ANALISI DEI CARICHI
o
o
o
o
o
o
PESO PROPRIO STRUTTURALE (G1)
CARICO PERMANENTE NON STRUTTURALE (G2)
CARICO VARIABILE DI ESERCIZIO (QS)
CARICO DA NEVE (QS)
CARICO DA VENTO (QW)
AZIONE SISMICA (E)
Per quanto riguarda l’effetto dei gradienti termici si può supporre
che sia compensato dalla sostanziale isostaticità della struttura e
dalla intrinseca deformabilità dei collegamenti.
PESO PROPRIO STRUTTURALE
Il peso proprio degli elementi strutturali è valutato nel seguito in
funzione del profilato adottato, tenuto conto del peso specifico
dell’acciaio.
CARICO PERMANENTE NON STRUTTURALE
Considereremo i seguenti sovraccarichi permanenti:
peso dei pannelli sandwich = 0.10 KN/m2
peso aggiuntivo (p.e. pannelli fotovoltaici) = 0.30 KN/m2
CARICO VARIABILE DI ESERCIZIO
Dalla tab. 3.1.II delle NTC
carico variabile di esercizio = 0.50 KN/m2 (coperture non praticabili
e accessibili per sola manutenzione)
11
CARICO DA NEVE
Come è noto l’espressione del carico da neve, secondo le NTC è la
seguente:
Dalla zonizzazione riportata dalle NTC (ZONA III) il carico da neve
al suolo caratteristico è qsk = 0.60 KN/m2 (as ≤200 m s.l.m.).
Per il coefficiente di esposizione si assumerà, in condizioni normale
esposizione al vento, CE = 1.00.
In assenza di specifici studi sul calore trasmesso dall’edificio alla
copertura si assume per il coefficiente termico Ct = 1.00.
Per quanto attiene al coefficiente di forma si devono considerare le
possibilità di accumulo della neve in presenza o in assenza di vento.
Nel caso della copertura a shed si dovrà fare riferimento alle
indicazioni riportate nella Circolare n.617.
12
La copertura a shed è costituita da falde verticali e inclinate di 25°.
Se ne deduce che, come ovvio, l’accumulo può aversi sulla falda
inclinata dello shed con μ1=0.80 e soprattutto nel compluvio, anche
in relazione all’effetto di ridistribuzione operato dal vento.
Quindi si potrebbe considerare il caso (i) con semplice distribuzione
di un carico pari a qs = 0.80·0.60 = 0.48 KN/m2 e il caso (ii) con
μ2= μ2((25+90)/2)=1.60, come in figura.
In via semplificata, data la poca differenza tra i due casi, e come
anche suggerito dalla circolare per inclinazioni inferiori a 25°, si
potrà considerare solo il caso (i) con una distribuzione sulla
proiezione orizzontale del carico di 0.48 KN/m2.
13
CARICO DA VENTO
Seguendo le indicazione delle NTC2008, tenuto conto che l’edificio
sorge nella cosiddetta ZONA 5 della zonizzazione nazionale,
corrispondente alla Sardegna Orientale e ad una quota sopra il
livello del mare pari a 0.00 m, si determinano i seguenti parametri:
dalla tab. 3.3.I delle NTC
velocità di riferimento del vento: Vb = 28 m/sec (per TR=50 anni)
quota sopra il livello del mare di riferimento: a0 = 750 m
Ka = 0.015 sec-1
pressione cinetica di riferimento: qb = 0.49 KN/m2
classe di rugosità: A
dalla tab.3.3.III delle NTC
categoria di esposizione: IV
14
Da cui:
dalla tab.3.3.II delle NTC
e quindi Ce =1.63 (valutato sul baricentro delle shed)
la pressione del vento è determinata in base alle espressioni fornite
dalle NTC:
PRESSIONE NORMALE:
AZIONE TANGENZIALE:
Oltre ai coefficienti già determinati si assumeranno:
coefficiente dinamico: Cd =1.00
coefficiente di attrito: Cf =0.01 (dalla Circ. N.617)
15
coefficiente
coefficiente
coefficiente
(α= 25°)
coefficiente
coefficiente
di forma per superfici verticali sopravento: Cpe =+0.80
di forma per superfici verticali sottovento: Cpe =-0.40
di forma per superfici inclinate sopravento: Cpe =-0.25
di forma per superfici inclinate sottovento: Cpe =-0.40
di forma interno: Cpi =±0.20 (edifici quasi stagni)
direzione N-S e S-N:
direzione E-O e O-E:
Sulla base dei parametri sopra riportati, si determina una pressione
del vento sulle pareti perimetrali che varia a seconda del segno
della pressione interna:
pressione del vento sopravento: Qsop =0.80 (0.48) KN/m2
depressione del vento sottovento: Qsop =0.16 (0.48) KN/m2
Inoltre, per quanto riguarda gli elementi di copertura, sulla base
delle indicazione della Circolare, si ha che i valori di pressione
agiscono al 100% nel primo shed investito dal vento, al 75% nei
successivi.
Quando il vento spira in direzione S-N investendo direttamente il
primo spiovente dello shed si ha una depressione che al massimo
raggiunge il valore di
0.48 KN/m2 ed è ridotta al 75% nei
16
successivi. Quando il vento spira in direzione N-S al massimo la
depressione nel primo shed sale a 0.36 KN/m2.
Quando il vento spira in direzione E-O e O-E, si considererà su tutta
la copertura una depressione che al massimo assume il valore 0.48
KN/m2, inoltre un’azione radente di minima entità pari a 0.008
KN/m2, distribuita su tutta la superficie della copertura.
La circolare inoltre suggerisce che per valutare le azioni di insieme
sulla struttura e quindi per dimensionare per esempio gli elementi
controventanti, si consideri, per vento spirante in direzione N-S (e
S-N), un’azione orizzontale distribuita sulla proiezione orizzontale
della copertura pari a 0.10·qb·Ce =0.08 KN/m2.
17
AZIONE SISMICA
La Normativa Tecnica attualmente vigente ha suddiviso il territorio
nazionale secondo una griglia ai cui nodi sono assegnati tutti i valori
dei parametri necessari a definire localmente l’azione sismica
(mappe di pericolosità INGV), in termini di accelerazione di
riferimento al suolo ag per sito rigido (terreno tipo A) e di spettri di
risposta elastici Se(T). La Sardegna fa parte di quelle aree del
territorio nazionale considerate a bassa sismicità (zona 4) e i
relativi parametri sono riportati in uno specifico allegato del
documento normativo.
Essendo l’edificio in Zona 4 le NTC al Cap.7 consentono una verifica
semplificata, secondo la quale la progettazione può essere condotta
come se l’edificio ricadesse in zona non sismica, a patto che:
o Gli
orizzontamenti
rispettino
specifiche
prescrizioni,
sostanzialmente finalizzate a garantire un comportamento a
diaframma rigido nel piano;
o Gli elementi strutturali e i dettagli costruttivi siano dimensionati
in modo da garantire una Classe di Duttilità bassa (CD”B”).
Ovvero la struttura deve garantire un comportamento
“mediamente” dissipativo in grado di sviluppare meccanismi di
rottura duttili (cerniere plastiche).
o Sia effettuata una verifica sismica semplificata, realizzata
applicando un’Analisi Statica lineare con azioni sismiche nelle
due direzioni principali ortogonali dell’edificio corrispondenti ad
un’accelerazione della struttura pari a 0.07g m/sec2 (0.69
m/sec2). Si faranno verifiche indipendenti nelle due direzioni e
solo agli effetti degli SSLLUU.
18
DESCRIZIONE “INTUITIVA” DEL FENOMENO SISMICO
Il sisma costituisce un movimento nelle 3 direzioni della crosta
terrestre e quindi del terreno su cui è fondato il manufatto. Lo
scuotimento del terreno si trasmette tramite le fondazioni (che
possiamo considerare solidali ad esso) alla struttura in elevazione.
Per l’effetto combinato dell’inerzia della struttura, quindi della sua
massa, e della rigidezza, la struttura segue il terreno nella sua
oscillazione, ma ne deriva delle deformazioni e in definitiva delle
sollecitazioni.
Salvo casi particolari, indicati chiaramente dalla norma, non ci si
interessa dell’oscillazione in direzione verticale del terreno, perché
in genere procura molti meno danni, ma solo delle oscillazioni
orizzontali.
I casi estremi della risposta dinamica di una struttura sono:
1) se la struttura fosse estremamente rigida oppure priva di massa,
si muoverebbe assieme alle fondazioni e al terreno sottostante e
non ne deriverebbe alcuna sollecitazione (non si deformerebbe);
2) se la struttura fosse eccessivamente flessibile o fosse dotata di
una massa enorme, quest’ultima tenderebbe a stare ferma mentre
le fondazioni si sposterebbero, ricevendo la massima deformazione
possibile.
Ovviamente il caso reale è intermedio fra i precedenti. Se l’edificio
fosse semplicemente un’unica massa connessa in qualche modo alle
19
fondazioni, dotata di un solo grado di libertà, potrebbe essere
considerata un oscillatore semplice (p.e. un serbatoio dell’acqua) e
in tal caso questo comportamento potrebbe essere condensato in
un unico parametro: il periodo di oscillazione (o la frequenza
propria), che dipende dalla massa e dalla rigidezza della struttura.
Questo periodo caratterizza la risposta dell’oscillatore semplice
sotto l’effetto di un’azione dinamica.
In altre parole se si sollecita con uno scuotimento orizzontale le
fondazioni della struttura le masse della stessa sarebbero
sottoposte a delle forze di trascinamento determinate dal modo col
quale sono connesse alle fondazioni (la struttura stessa, p.e. i
pilastri) e nello stesso tempo si opporrebbero a tale spostamento
con delle forze d’inerzia pari all’accelerazione del terreno per la
massa.
L’equazione che governa il fenomeno è quella che deriva
dall’applicazione della seconda legge di Newton (o il Principio di
D’Alambert):
&& + cu& + ku = −Mu
&&g
Mu
&& = forza d’inerzia legata all’accelerazione della massa;
Mu
cu& = forze dissipative legate a fenomeni come la viscosità;
ku = forze statiche di richiamo elastico, dovute alla “struttura”;
&&g = forza di trascinamento dovuta al moto del terreno;
Mu
si potrà ricavare che:
f = 1 2π k M = frequenza propria o naturale dell’oscillatore;
T =1 f =
periodo proprio dell’oscillatore;
20
Il fenomeno sismico potrà essere ricondotto ad una forza di tipo
inerziale applicata alle masse della struttura, come si deduce dalla
relazione precedente. Infatti:
quando
u& = 0
u = uMax
(u&& + u&& g ) = u&& ass = u&& ass,Max
e quindi:
&&ass,Max = kuMax
Mu
La massima forza di richiamo elastica, coincide con la massima
forza di inerzia in termini di accelerazione assoluta, quindi
entrambe possono fornirci la massima sollecitazione nella struttura.
Ma qual è il valore di accelerazione da applicare a queste
masse? Nel caso dell’oscillatore semplice infinitamente rigido
(T=0) la risposta è immediata: l’accelerazione del terreno.
Poiché le strutture reali non sono oscillatori semplici, né
infinitamente rigide, nel senso che sono costituite da più masse in
qualche modo connesse, il discorso si complica, perché esistono più
forme di oscillazione (modi) cui competono distinti periodi propri. In
realtà esistono tanti modi di vibrare quanti sono i gradi di libertà e
possono essere studiati effettuando un’Analisi Modale.
Spesso però, per strutture dotate di una certa regolarità
distributiva, soprattutto in altezza, di massa e rigidezza (strutture
semplici) il periodo fondamentale della struttura, ovvero quello
21
corrispondente al primo modo di vibrare (in genere un’oscillazione
semplice delle masse) è quello dominante e si può trattare la
struttura come se fosse un oscillatore semplice.
La normativa fornisce i cosiddetti spettri di risposta in
accelerazione, ovvero dei diagrammi che in funzione del periodo
proprio (in generale anche dello smorzamento) della struttura,
intesa come oscillatore semplice, forniscono il valore di
accelerazione assoluta massima che subisce la struttura. Questi
diagrammi sono stati dedotti dai normatori a partire dagli
accelerogrammi dei fenomeni sismici rilevati negli ultimi decenni sul
territorio nazionale.
a(t)
(m/sec2)
t (sec)
Questi
accelerogrammi
possono
essere
rielaborati
come
sommatoria di funzioni armoniche (Trasformata di Fourier) e si può
ottenere la soluzione dell’equazione differenziale dell’oscillatore
semplice, ponendo tali accelerazioni armoniche al secondo membro
della stessa e sovrapponendone infine gli effetti.
22
Quindi si possono ottenere lo spostamento massimo e/o
l’accelerazione massima della struttura, ovvero la massima
sollecitazione indotta dal sisma.
Ripetendo l’operazione per diversi tipi di oscillatore, con diverso
periodo proprio e diverso smorzamento si possono ottenere gli
spettri di risposta in accelerazione (o spostamento) cercati, per un
determinato fenomeno sismico.
Questi diagrammi, secondo l’ultima impostazione normativa
possono essere costruiti punto per punto nel territorio nazionale, in
base alla mappa di pericolosità sismica INGV, secondo una serie di
parametri forniti negli allegati alle NTC in ragione del periodo di
ritorno TR (ovvero dello Stato Limite considerato) secondo
opportune espressioni riportate nel Cap.3.
23
STATI LIMITE PER L’AZIONE SISMICA
(in ordine di gravità)
In generale si considerano i seguenti Stati Limite d’Esercizio:
Stato Limite di Operatività (SLO): a seguito del terremoto la
costruzione nel suo complesso, includendo gli elementi strutturali,
quelli non strutturali, le apparecchiature rilevanti alla sua funzione,
non deve subire danni ed interruzioni d'uso significativi (PVR=81%);
Stato Limite di Danno (SLD): a seguito del terremoto la
costruzione nel suo complesso, includendo gli elementi strutturali,
quelli non strutturali, le apparecchiature rilevanti alla sua funzione,
subisce danni tali da non mettere a rischio gli utenti e da non
compromettere significativamente la capacità di resistenza e di
rigidezza nei confronti delle azioni verticali ed orizzontali,
mantenendosi immediatamente utilizzabile pur nell’interruzione
d’uso di parte delle apparecchiature (PVR=63%);
E i seguenti Stati Limite Ultimi:
Stato Limite di salvaguardia della Vita (SLV): a seguito del
terremoto la costruzione subisce rotture e crolli dei componenti non
strutturali ed impiantistici e significativi danni dei componenti
strutturali cui si associa una perdita significativa di rigidezza nei
confronti delle azioni orizzontali; la costruzione conserva invece una
parte della resistenza e rigidezza per azioni verticali e un margine
di sicurezza nei confronti del collasso per azioni sismiche orizzontali
(PVR=10%);
Stato Limite di prevenzione del Collasso (SLC): a seguito del
terremoto la costruzione subisce gravi rotture e crolli dei
componenti non strutturali ed impiantistici e danni molto gravi dei
componenti strutturali; la costruzione conserva ancora un margine
di sicurezza per azioni verticali ed un esiguo margine di sicurezza
nei confronti del collasso per azioni orizzontali (PVR=5%);
dalla tabella 3.2.I delle NTC.
24
ANALISI STATICA LINEARE
Come evidente il problema è inerentemente dinamico e pertanto
l’analisi strutturale dovrebbe essere condotta su base dinamica e in
campo non lineare, per tenere conto delle risorse dissipative della
struttura. Ma la norma consente l’uso dell’Analisi Statica lineare,
che è il metodo di più semplice e può essere utilizzato, con
opportune semplificazioni e, per strutture semplici, anche per
effettuare calcoli a mano.
L’azione sismica viene schematizzata attraverso una data
distribuzione di forze d’inerzia (proporzionali alle masse
della struttura) applicate staticamente. Quindi si procede ad
una normale analisi strutturale statica.
Tale semplificazione del fenomeno sismico è lecita solo per edifici
che rispettano certi requisiti, p.e. la regolarità in altezza e quando
non siano troppo deformabili, ovvero che il periodo del modo
principale di vibrare T1 non sia troppo elevato (vengono fornite le
limitazioni). In questi edifici è lecito assumere a priori una
determinata distribuzione delle azioni sismiche, poiché in essi il
primo modo di vibrare flessionale è nettamente prevalente.
Per edifici non troppo alti (H < 40 m) e con distribuzione di massa
in altezza regolare, si può stimare (senza fare un’analisi modale):
3
4
T1 = C1 ⋅ H (sec)
25
H = altezza dell’edificio dal piano di fondazione (m);
C1 = 0,085 per strutture a telaio in acciaio
Una volta noto il periodo principale dell’edificio si entra nello
SPETTRO DI RISPOSTA DI PROGETTO in accelerazione che viene
fornito dalla normativa per ognuno degli Stati Limite presi in
considerazione.
L’ordinata dello spettro di progetto relativo ad un determinato Stato
Limite, corrispondente a T1, fornisce il valore di base Sd(T1) per la
determinazione dell’AZIONE SISMICA Fh. Tale valore di Sd è
un’accelerazione e verrà moltiplicata per la massa complessiva
dell’edificio.
Una volta determinata l’azione complessiva Fh (taglio alla base),
questa sarà poi distribuita tra le varie masse in cui abbiamo
schematizzato l’edificio in proporzione alle stesse e all’altezza,
secondo la relazione:
Fi = Fh ⋅
zi ⋅ Wi
∑ z j ⋅ Wj
j
26
La reale risposta non lineare di una struttura corrispondente alla
plasticizzazione o al danneggiamento (murature) è fonte di
dissipazione dell’energia cinetica indotta dal sisma. Questo
effetto è benefico perché sottrae energia cinetica e quindi riduce
l’accelerazione assoluta imposta alle strutture e agli elementi
portati, riducendone il danneggiamento.
Tutto questo ha senso solo se in campo non lineare gli elementi
possono offrire una certa duttilità, diversamente si ha una
pericolosa rottura di schianto!!
Anche se l’analisi è lineare questi effetti dissipativi vengono presi in
conto attraverso una forfetaria riduzione dell’azione sismica a
mezzo del FATTORE DI STRUTTURA con cui è scalata l’azione
sismica Fh (infatti si è scalato lo spettro elastico di progetto). Tale
fattore viene fornito dalla normativa e dipende tra le altre cose
dalla tipologia dell’edificio e dalla regolarità (in pianta).
L’analisi elastica lineare è appropriata per strutture che si
deformino principalmente in funzione del primo modo di vibrare. I
modi superiori sono poco influenti. Allora è lecito trattare la
struttura come se fosse ad un solo grado di libertà.
Ecco perché questo è in genere permesso solo per strutture
REGOLARI IN ALTEZZA (si veda la norma per le condizioni).
Nel caso in esame, si può ipotizzare che tutta la massa sottoposta
all’accelerazione sismica sia concentrata alla quota della copertura
(trascurando la massa distribuita su tamponamenti e i pilastri)
pertanto si considererà che tutta l’azione sismica venga scaricata
sul baricentro della copertura e sia generata dal “peso sismico” di
quest’ultima.
27
SPETTRI DI RISPOSTA
Per esempio nel caso in esame, possiamo tracciare gli spettri di
risposta relativi allo Stato Limite di Danno SLD (esercizio) e lo Stato
Limite di Salvaguardia della vita SLV (ultimo).
Data la natura dell’edificio e la sua destinazione d’uso sono stati
determinati i parametri:
Vita nominale VN = 50 anni
Classe d’uso II per edifici con normali affollamenti: Cu = 1.0
Da questi si determina il periodo di riferimento per gli eventi
naturali VR = VR·Cu =50 anni.
Sulla base di questo periodo temporale si deve dedurre il periodo di
ritorno TR dell’evento sismico, tenendo conto che la probabilità di
superamento nel SLD è del 63% (50 anni) nel periodo di
riferimento VR e nello SLV è del 10% (475 anni).
Dalla Tabella 2 allegata al testo del Decreto, si ricavano:
SLD (TR = 50 anni)
ag = accelerazione di riferimento al suolo PGA = 0.235 (m/sec2)
F0 = massimo valore del fattore di amplificazione dello spettro = 2.67
TC* = periodo di riferimento per il tratto a velocità costante = 0.296 (sec)
SLV (TR = 475 anni)
ag = accelerazione di riferimento al suolo PGA = 0.50 (m/sec2)
F0 = massimo valore del fattore di amplificazione dello spettro = 2.88
TC* = periodo di riferimento per il tratto a velocità costante = 0.34 (sec)
Da questi si ricavano gli spettri di risposta elastici e di progetto già riportati,
relativi alla componente orizzontale del sisma (quella verticale non sarà presa
in considerazione). In essi il tratto ad accelerazione costante si ha per periodi
superiori a TB =TC/3 = CC·TC*/3 che assume i seguenti valori:
TB_SLD = 0.138 sec
TB_SLV = 0.155 sec
Si noti che nella determinazione dello spettro di progetto entrano in
gioco, attraverso i coefficienti Cc ed S, le caratteristiche locali del
terreno e quelle topografiche del sito in cui sorge il manufatto (vedi
relazione geologico-geotecnica).
28
Ipotizzeremo cautelativamente che il terreno sia di cat.B, e di categoria
stratigrafica T1 per superfici pianeggianti. Tutto questo viene preso in conto
con una serie di coefficienti amplificativi che culminano nel coefficiente S= 1.20
Lo spettro di risposta elastico coincide con quello di progetto nel caso dello
SLD, mentre quello allo SLV si deduce da quello elastico introducendo il fattore
di struttura che tiene conto delle risorse dissipative del manufatto. In questo
caso, per una struttura esistente a telaio in acciaio con schema a mensola,
seguendo le indicazioni della Circolare si porrà q= 2.00.
Nel grafico che precede si è anche individuato con una certa approssimazione il
periodo fondamentale della struttura T1, determinato secondo la formula
empirica:
T1 = C1·H¾ = 0.40 sec
posto C1 = 0.085
H= 8.00 m (altezza dell’edificio nel baricentro della copertura)
Da cui si ricavano i seguenti valori per l’accelerazione spettrale orizzontale:
Sd,SLD(T1)= 0.077g m/sec2
Sd,SLV(T1)= 0.088g m/sec2
Come si può osservare avendo assunto un terreno di cat. B l’accelerazione allo
SLV è maggiore di quella richiesta nel metodo semplificato (0.07g).
29
COMBINAZIONE SISMICA
Le verifiche sismiche vengono effettuate con riferimento alla
seguente combinazione:
In cui si nota che l’azione sismica si considera contemporanea ai
carichi permanenti e alla quota quasi permanente dei carichi
variabili (ψ2).
Le masse che generano l’azione sismica sono peraltro quelle
corrispondenti a questa espressione (“pesi sismici”):
I coefficienti sono dedotti dalla tabella 2.5.I delle NTC
Si nota perciò che le azioni del vento, della neve e di esercizio, sono
poco significative e non si considerano contemporanee all’evento
sismico. Nel seguito ci si limiterà pertanto a valutare il solo peso P
della copertura tenuto conto di tutti gli elementi strutturali e il
sovraccarico permanente e moltiplicare per l’accelerazione sismica:
Fh = Sd(T1) ⋅ W ⋅ λ/g = 0.07 ⋅ W
30
CORSO DI COSTRUZIONI
IN ACCIAIO
270 Laurea Magistrale
I anno – I semestre
ESERCITAZIONE:
CALCOLO DELLA STRUTTURA DI UN CAPANNONE
INDUSTRIALE SITO NELLA CITTÀ DI CAGLIARI
Parte 2
TITOLARE: Prof. Ing. Barbara De Nicolo
RELATORE: Ing. Daniel Meloni
VERIFICA DEGLI ARCARECCI
Nel seguito si inizierà col prendere in esame gli arcarecci della struttura
precedentemente descritta, dei quali si eseguirà il predimensionamento e la
verifica.
I dati geometrici essenziali relativi agli arcarecci sono:
luce di calcolo L= 4.00 m
interasse medio int = 0.86 m (0.78 m in proiezione orizzontale)
inclinazione α= 25°
1
ANALISI DEI CARICHI
Sovraccarico permanente: QP= 0.40 KN/m2
Sovraccarico variabile: QV= 0.50 KN/m2
Carico da neve: QS= 0.48 KN/m2
È inutile prendere in considerazione il carico del vento dal momento
in cui ha su tutte le falde effetto di depressione e avendo quindi
segno contrario rispetto agli altri carichi, peraltro più determinanti
agli effetti delle verifiche. Questo carico potrebbe essere preso in
considerazione per la valutazione di sicurezza dei mezzi di
connessione dei pannelli di copertura all’orditura di supporto.
Considerando l’area di pertinenza dell’arcareccio più caricato
(arcareccio intermedio), con riferimento ai carichi agenti sulla
copertura possiamo passare dal valore di questi sulla superficie al
valore distribuito sulla lunghezza dell’arcareccio.
qP = 0.40 ·0.86 = 0,34 KN/m
qv = 0.50 ·0.86 = 0,43 KN/m
qn = 0.48 ·0.78 = 0,37 KN/m
Sviluppiamo le combinazioni di calcolo da prendere in esame:
combinazione fondamentale allo SLU:
2
da cui (a meno del peso proprio dell’elemento):
qSLU,1 = 1.30·0.34+1.5·(0.43+0.5·0.37) = 1,36 KN/m
qSLU,2 = 1.30·0.34+1.5·(0.37+0·0.43) = 1,00 KN/m
da cui si deduce immediatamente quale sia l’unica combinazione
che vale la pena di considerare.
combinazione caratteristica (rara) per lo SLE:
qSLE = 0.34+0.43+0.5·0.37 = 0.96 KN/m
L’arcareccio, in virtù della sua inclinazione rispetto alla direzione del carico
(piano di flessione), è sottoposto a sollecitazioni di FLESSIONE e TAGLIO
DEVIATI.
La componente del carico: qy = q·cos(25°)
genera:
Mx = flettente che ruota attorno all’asse
x-x
Ty = taglio diretto secondo l’asse y-y
La componente qx = q·sen(25°)
genera:
My = flettente che ruota attorno all’asse
y-y
Tx = taglio diretto secondo l’asse x-x
MATERIALI
Ipotizzeremo l’uso di profilati laminati a caldo realizzati con acciaio
duttile di grado S235JR conforme alla norma armonizzata UNI EN
10025 (ex Fe360B). Tale materiale è caratterizzato dalle seguenti
proprietà meccaniche:
3
modulo di elasticità = 210000 MPa
carico unitario di rottura ftk = 360 MPa
carico unitario di snervamento fyk = 235 MPa
per le verifiche di resistenza la norma fa riferimento ai seguenti
coefficienti di sicurezza:
dalla Tab. 4.2.V
PREDIMENSIONAMENTO
I profili commerciali più comunemente utilizzati per la realizzazione
di arcarecci di copertura sono profili ad Ω (in genere profilati a
freddo), UPN e profili a doppio T (IPE, HEA, HEB).
Ipotizziamo di lavorare con questi ultimi. Questo genere di profili
sono detti a sezione compatta (CLASSE 1 e 2) e per essi è lecito
l’uso del metodi elastico e plastico per la verifica allo SLU.
Nella scelta del profilo ci si può basare sull’esperienza, oppure si
effettuano dei calcoli preliminari che possono orientare la scelta. In
tal caso entrambe le tipologie di verifica, allo SLU e SLE devono
essere tenute in conto, perché spesso è la verifica allo SLE di
deformabilità che risulta essere dimensionante.
4
In via semplificata, trascuriamo l’inclinazione dell’arcareccio e
consideriamo la flessione retta. Allo SLU, a meno del peso proprio il
momento flettente di calcolo è dato da:
MED = qSLU·L2/8 = 2.72 KNm
ipotizzando il comportamento elastico della sezione e trascurando
l’azione tagliante (facendo quindi riferimento alla sola tensione
normale indotta dalla flessione), possiamo determinare il minimo
modulo di resistenza della sezione cercata:
essendo:
σx,Ed = MED/Wel,min = fyk/γM0
Wel,min = MED/(fyd/γM0)= 2.72·106/(235/1.05)=12153 mm3
I profili commerciali che soddisfano tale requisito sono p.e. (in
ordine crescente di peso): IPE80, IPE100, HEA100, HEB100.
Verifichiamo ora le proprietà deformative del profilo cercato.
Cercheremo una sezione che offra un’inerzia sufficiente perché le
deformazioni in esercizio dell’elemento non siano tali da provocare,
in generale, effetti estetici e funzionali indesiderati, tra cui il
danneggiamento degli elementi portati.
fmax
5 qSLE ⋅ L4
=
⋅
384 E ⋅ Jmin
Il limite ammissibile della freccia è determinato dal progettista in
funzione delle esigenze di cui sopra. Nel nostro caso, la copertura
non è praticabile e non richiede particolari attenzioni per quanto
riguarda le strutture portate, quindi ci si potrà riferire alle
indicazioni fornite dalla normativa per le coperture in generale
(Tab.4.2.X):
5
δmax = freccia dovuta al carico totale = L/200
δ2 = freccia dovuta al solo carico variabile = L/250
Facendo riferimento alla prima limitazione, ipotizzando che la
freccia dovuta al peso proprio sia compensata da una leggera
controfreccia, scriviamo:
5 0.96 ⋅ (4.00 ⋅ 103 ) 4.00 ⋅ 103
=
⋅
=
384
210000 ⋅ Jmin
200
4
fmax = δmax
da ciò si ricava che Jmin = 761905 mm4
I profili che soddisfano tale requisito sono p.e. (in ordine
crescente): IPE80, IPE100, HEA100, HEB100.
Ipotizziamo di scegliere come profilo un IPE80 ed effettuiamo le
verifiche. Il profilo ha le seguenti caratteristiche:
H = 80 mm
B = 46 mm
sa = 3.8 mm
sf = 5.2 mm
Wx = 20000 mm3
Wy = 3690 mm3
Wpl,x = 23200 mm3
Wpl,y = 5820 mm3
Jx = 801000 mm4
Jy = 84900 mm4
ρ = 6.0 Kg/m
NOTA: attenzione in questo esempio si indicheranno rispettivamente con y e x
l’asse forte e l’asse debole. Wx e Jx fanno riferimento alla flessione attorno a x
(asse debole) e quindi in direzione y (asse forte).
6
Vediamo a quale classe appartiene il profilo che abbiamo scelto. La
normativa fornisce dei prospetti che consentono di giudicare in base
a requisiti di tipo geometrico, la classe dell’elemento e quindi la
possibilità di applicazione del Metodo Plastico di verifica.
Tab. 4.2.I
Come si vede dalla tabella, si fa riferimento alla snellezza
dell’anima, perché è il sopraggiungere di episodi di instabilità
locale che può prevenire ed impedire il raggiungimento della
completa plasticizzazione della sezione.
Analogamente si dovrà verificare l’occorrenza di instabilità nelle
piattabande:
7
Tab. 4.2.II
Nel nostro caso la situazione è la seguente:
per l’anima:
c = 80 – 2·5.2 – 2·5 =59.6
t = sa = 3.8
ε = 1 (S235)
da cui: c/t = 15.7 < 72 ε
per la piattabanda:
c = (55 – 3.8 – 2·5 )/2=20.6
t = sf = 5.2
ε = 1 (S235)
da cui: c/t = 3.96 < 9 ε
se ne deduce che il profilo prescelto ha Classe 1. Questo significa
che la sezione può interamente plasticizzarsi, sviluppare una
resistenza maggiorata tramite il modulo plastico (> del modulo di
resistenza elastico) e subire notevoli rotazioni che la fanno
comportare come una cerniera plastica. Con una sezione di questo
8
genere è ammesso il Metodo di verifica Plastico, che è più
vantaggioso perché presuppone un migliore sfruttamento delle
risorse del materiale, ma è talvolta più complesso da applicare. Per
semplicità utilizzeremo il Metodo Elastico, che è applicabile a tutte
le tipologie di sezione.
VERIFICA ALLO SLU DI FLESSIONE
Valutiamo le due componenti del carico con riferimento alla
combinazione allo SLU prescelta, tenendo presente che in campo
elastico è valido il PRINCIPIO DI SOVRAPPOSIZIONE DEGLI
EFFETTI:
qSLU = 1.36 + 1.3·0.06= 1.44 KN/m (aggiungiamo il peso proprio)
qy = qSLU·cos(25°)= 1.30 KN/m Mmax,x = 2.60 KNm
qx = qSLU·sen(25°)= 0.61 KN/m Mmax,y = 1.21 KNm
Mmax,x
2.60 x 106
σmax,x =
=
= 130 N/mm2
Wx
20000
Mmax,y
1.21 x 106
σmax,y =
=
= 328 N/mm2
Wy
3690
9
σx-max
H/2
H
σy-max
+
B/2
B
σx-max
=
σy-max
la verifica si effettua secondo la formula:
in cui le tensioni normali sono indicate come σx,Ed e sono ottenute
come sovrapposizione delle due flessioni rette. Non ha senso
prendere in considerazione la sollecitazione tagliante nella sezione
di mezzeria, inoltre non ci sono tensioni normali nel piano della
sezione, quindi:
σx,Ed2 = (σmax,x + σmax,y)2 = (130 + 328)2 ≤ (235/1.05)2 NO!!
Come si può constatare la verifica è nettamente negativa, quindi
dobbiamo passare ad una sezione superiore.
Ipotizziamo di scegliere come profilo un IPE120 ed effettuiamo le
verifiche. Il profilo ha le seguenti caratteristiche:
H = 120 mm
B = 64 mm
sa = 4.4 mm
sf = 6.3 mm
Wx = 53000 mm3
Wy = 8650 mm3
Wpl,x = 60700 mm3
Wpl,y = 13580 mm3
Jx = 3180000 mm4
Jy = 277000 mm4
ρ = 10.4 Kg/m
Si può facilmente verificare che la il profilo ha ancora Classe 1.
10
qSLU = 1.36 + 1.3·0.10= 1.50 KN/m
qy = qSLU·cos(25°)= 1.36 KN/m Mmax,x = 2.72 KNm
qx = qSLU·sen(25°)= 0.63 KN/m Mmax,y = 1.26 KNm
Mmax,x
2.72 x 106
=
= 51.3 N/mm2
Wx
53000
M
1.26 x 106
= max,y =
= 145.7 N/mm2
Wy
8650
σmax,x =
σmax,y
σx,Ed2 = (σmax,x + σmax,x)2 = (51.3 + 145.7)2 = (197)2 ≤ (235/1.05)2 (OK)
OSSERVAZIONI:
1) La flessione deviata ha reso la verifica estremamente critica e
costretto all’uso di un profilo pesante. Sarebbe opportuna la scelta
di un altro profilo ottimizzato rispetto alla flessione attorno all’asse
debole. Probabilmente la scelta migliore sarebbe un profilo ad Ω;
2) non si è scelto un profilo del tipo HEA o HEB perché di fatto più
costoso (sono più pesanti).
3) In queste situazioni emerge la convenienza del Metodo Plastico,
infatti si dimostra che la verifica col Metodo Elastico non avrebbe
dato esito positivo neanche per un profilo IPE100, ma se si fossero
prese in considerazione le risorse plastiche della sezione
quest’ultimo profilo sarebbe stato sufficiente.
VERIFICA ALLO S.L.U. DI TAGLIO
La verifica verrà effettuata agli appoggi. La distribuzione delle
tensioni di taglio nella sezione è tale che rispetto a Tx e Ty le parti
resistenti sono rispettivamente costituite dall’anima o dalle flange
ed è pressoché trascurabile nel resto della sezione. La reale
distribuzione è quella fornita dalla formula del Jourawski. Per
semplicità si usa considerare una distribuzione uniforme sulla parte
resistente della sezione, cioè si approssima la tensione massima a
quella media.
qy = qSLU·cos(25°)= 1.36 KN/m
qx = qSLU·sen(25°)= 0.63 KN/m
Tmax,y = 2.72 KN
Tmax,x = 1.26 KN
11
per il taglio agente nel piano dell’anima (Ty) si considererà reagente
solo quest’ultima, secondo l’espressione fornita dalla norma:
Av = A -2b·sf + (sa + 2r) ·sf = 629.5 mm2
per il taglio agente nel piano delle ali (Tx) si considererà reagenti le
sole ali, secondo l’espressione fornita dalla norma:
Av = A -∑(ha·sa) = 909 mm2
τx-med =
Tx-max
1.26 x 1000
=
= 1.39 N/mm2 (τzx)
AV
909
τy-med =
Ty-max
AV
=
2.72 x 1000
= 4.32 N/mm2 (τzy)
630
τx-max
τy-max
H/2
H
B
Le tensioni dovrebbero essere composte, ma non raggiungono il
massimo valore contemporaneamente negli stessi punti, anzi τx è
diversa da zero dove è nulla la τy e viceversa, quindi:
τx-med = 4.31 N/mm2 < (fyk / γ M0 )/ 3 = 129 N/mm2 (OK)
τy-med = 1,56 N/mm2 < (fyk / γ M0 )/ 3 = 129 N/mm2 (OK)
Il taglio agente sull’elemento ha valore così basso da non
influenzare in alcun modo la resistenza flessionale dello stesso.
12
VERIFICA ALLO S.L.U. DI INSTABILITÀ FLESSO-TORSIONALE
Verifichiamo ora la possibilità di occorrenza di un’instabilità flessotorsionale (svergolamento) dell’arcareccio, sotto i carichi della
combinazione allo SLU, sulla luce libera di 4.00 m.
In via semplificata supporremo di considerare il caso di flessione
retta.
Come primo passo si determina la SNELLEZZA ADIMENSIONALE
λ LT , ma per farlo devo determinare il MOMENTO CRITICO ELASTICO
DI INSTABILITÀ TORSIONALE DELLA SEZIONE. La modalità per
determinare quest’ultimo è riportata nella Circolare n.617.
(attenzione la simbologia delle NTC è incoerente con quella utilizzata in questi
appunti soprattutto rispetto agli assi d’inerzia della sezione)
Iniziamo col determinare il momento critico, tenendo conto che:
Lcr = lunghezza libera di instabilità laterale, che nel nostro caso
assumeremo pari all’intera luce di 4.00 m;
EJy = rigidezza flessionale laterale (asse debole), nel nostro caso
pari a 210000·277000 =5.817·1010;
GJT = rigidezza torsionale, nel nostro caso pari a 80769·17350
=14.01·108;
EJw = rigidezza torsionale secondaria, nel nostro caso pari a
210000·890·106 =1.869·1014;
ψ = coefficiente che tiene conto della distribuzione del momento
flettente lungo l’asse dell’elemento. La norma dice di fare
riferimento ad una distribuzione di momenti uniforme, in tal caso il
coefficiente vale 1.
da ciò si deduce che per il nostro IPE120 sulla luce di 4.00 m:
13
14
π
 π  1.869 ⋅ 10
10
8
Mcr = 1 ⋅
5.817 ⋅ 10 ⋅ 14.01 ⋅ 10 ⋅ 1 + 
=
 ⋅
8
4000
 4000  14.01 ⋅ 10
= 7376162 Nmm = 7.38 KNm
2
Considerando quindi il modulo di resistenza plastico Wy=60700
mm3:
60700 ⋅ 235
λLT =
= 1.39
7376162
Una volta nota la snellezza posso determinare il FATTORE DI
RIDUZIONE DELLA RESISTENZA per effetto dell’instabilità:
con
f tiene conto della reale distribuzione del momento flettente tra i
ritegni torsionali, che non è uniforme e considera un fattore
correttivo kc che si deduce dalla tabella 4.2.VIII delle NTC e vale nel
nostro caso 0.94. in definitiva f = 0.99;
λLT,0 può essere assunto in generale pari a 0.2;
β può essere assunto in generale pari a 1;
α LT è il FATTORE DI IMPERFEZIONE riportato nella tab. 4.2.VI delle
NTC, una volta stabilita la curva di instabilità che caratterizza il
nostro profilo. In base alla tab. 4.2.VII si deduce che al nostro
profilo (laminato con H/B≤2) appartiene la curva di instabilità b e
dalla Tab. 4.2.VI deduciamo che α LT =0.34
14
tab. 4.2.VII
In definitiva:
Φ LT = 1.67
χ LT = 0.39
La nostra verifica si conclude determinando il momento resistente
di calcolo per i fenomeni di instabilità, pari a:
Mb,Rd = χ LT ⋅ Wy ⋅
fyk
γ M1
= 0.39 ⋅ 60700 ⋅
235
= 5298242 Nmm = 5.30 KNm
1.05
Il momento sollecitante complessivo allo SLU (nell’ipotesi di
flessione retta) è invece:
MEd = 3.00 KNm
Pertanto la verifica è soddisfatta.
VERIFICA ALLO S.L.E. DI DEFORMABILITÀ
Verifichiamo ora la deformabilità del profilo prescelto. Come già
discusso assumeremo i seguenti limiti:
δmax = freccia dovuta al carico totale = L/200
δ2 = freccia dovuta al solo carico variabile = L/250
Il carico totale allo SLE (a meno del peso proprio) è dato da:
qSLE = 0.34+0.43+0.5·0.37 = 0.96 KN/m
Il solo variabile porge:
qSLE,v = 0.43+0.5·0.37 = 0.62 KN/m
15
qSLE,y = qSLE·cos(25°) = 0.87 KN/m
qSLE,x = qSLE·sen(25°) = 0.41 KN/m
qSLE,v,y = qSLE,v·cos(25°) = 0.56 KN/m
qSLE,v,x = qSLE,v·sen(25°) = 0.26 KN/m
qy fy (spostamento lungo l’asse y-y)
fx
qx fx (spostamento lungo l’asse y-y)
f tot
fy
Poiché supporremo che lo schema sia
di semplice appoggio in entrambe le
direzioni, si porrà sempre:
fmax =
5 q ⋅ L4
⋅
384 E ⋅ J
Facendo riferimento al carico totale si determina:
4
5 qSLE,y ⋅ L
5 0.87 x (4.00 ⋅ 103 )4
fy =
=
⋅
= 4.34 mm
384 E ⋅ Jx
384 210000 x 3180000
4
5 qSLE,x ⋅ L
5 0.41 x (4.00 ⋅ 103 )4
fx =
=
⋅
= 23.5 mm
384 E ⋅ Jy
384 210000 x 277000
da cui:
ftot = fy·cos(25°)+fx·sen(25°) = 13.86 mm <
l
200
= 20 mm (OK)
16
analogamente per il solo carico variabile:
4
5 qSLE,v,y ⋅ L
5 0.56 x (4.00 ⋅ 103 )4
fy =
=
⋅
= 2.79 mm
384 E ⋅ Jx
384 210000 x 3180000
4
5 qSLE,v,x ⋅ L
5 0.26 x (4.00 ⋅ 103 )4
⋅
fx =
=
= 14.90 mm
384 E ⋅ Jy
384 210000 x 277000
da cui:
ftot = fy·cos(25°)+fx·sen(25°) = 8.82 mm <
l
= 16 mm (OK)
250
17
CORSO DI COSTRUZIONI
IN ACCIAIO
270 Laurea Magistrale
I anno – I semestre
ESERCITAZIONE:
CALCOLO DELLA STRUTTURA DI UN CAPANNONE
INDUSTRIALE SITO NELLA CITTÀ DI CAGLIARI
Parte 3
TITOLARE: Prof. Ing. Barbara De Nicolo
RELATORE: Ing. Daniel Meloni
ELEMENTI DELLO SHED
Si procederà ora al calcolo del montante e del diagonale che costituiscono lo
shed. Si richiama sotto lo schema di riferimento.
I dati geometrici essenziali relativi agli elementi dello shed sono:
altezza del montante H= 1.80 m (1.70 in asse)
lunghezza diagonale L= 4.10 m
inclinazione α= 25°
ANALISI DEI CARICHI
Dall’analisi precedente si possono determinare le reazioni di
appoggio degli arcarecci:
reazione di appoggio carico permanente Rp = 0.88 KN
reazione di appoggio carico da neve Rn = 0.74 KN
reazione di appoggio carico variabile Rv = 0.86 KN
pertanto allo stato limite ultimo si potrà porre:
RSLU = 1.3·0.88+1.5(0.86+0.5·0.74) =2.99 KN ~ 3.00 KN
Per gli arcarecci di estremità, poiché la pertinenza è la metà, si
potrà porre:
R’SLU = RSLU/2 = 1.50 KN
1
MATERIALI
Ipotizzeremo l’uso di profilati laminati a caldo realizzati con acciaio
duttile di grado S235JR conforme alla norma armonizzata UNI EN
10025 (ex Fe360B). Tale materiale è caratterizzato dalle seguenti
proprietà meccaniche:
modulo di elasticità = 210000 MPa
carico unitario di rottura ftk = 360 MPa
carico unitario di snervamento fyk = 235 MPa
ANALISI DELLE SOLLECITAZIONI E PREDIMENSIONAMENTO
Lo shed è una sottostruttura che può essere schematizzata come
sotto:
Si nota però che in alcuni campi lo shed è costituito dal diagonale
direttamente connesso sulla trave principale a mezzo di un
collegamento bullonato. Possiamo pertanto dimensionare questo
elemento ed utilizzare tale dimensionamento per il resto degli
elementi, montante compreso. Faremo pertanto riferimento a
questo schema:
2
Massimo momento (mezzeria) MED = 6.61 KNm
Massimo taglio (in appoggio) VED = 5.55 KN
Massima compressione/trazione NED = 2.27 KN
Supponendo di adottare il metodo elastico:
essendo:
σx,Ed = MED/ Wel,min = fyk/γM0
Wel,min = MED/(fyd/γM0)= 6.61·106/(235/1.05)=29534 mm3
3
I profili commerciali che soddisfano tale requisito sono p.e. (in
ordine crescente di peso): IPE100, HEA100, HEB100. Supponiamo
di adottare un IPE100
H = 100 mm
B = 55 mm
sa = 4.1 mm
sf = 5.7 mm
Wy = 34200 mm3
Wpl,y = 39400 mm3
Jy = 1710000 mm4
Jz = 159000 mm4
ρ = 0.08 KN/m
Il profilo ha Classe 1.
VERIFICA ALLO SLU DI FLESSIONE
Per effettuare le verifiche dobbiamo aggiungere l’effetto del peso
proprio:
MED = 6.61 +1.3·0.08·4.102/8= 6.83 KN/m
MED
6.83 x 106
σED =
= 199.7 N/mm2 < 235/1.05 (OK)
=
Wy
34200
VERIFICA ALLO S.L.U. DI TAGLIO
VED = 5.55 +1.3·0.08·4.10/2= 5.76 KN
Av = A -2b·sf + (sa + 2r) ·sf = 508 mm2
4
τED =
VED
5.76 x 1000
=
= 11.34 N/mm2< (fyk / γ M0 )/ 3 (OK)
AV
508
Non è significativo effettuare verifiche che tengano conto dell’azione
assiale, perché di piccola entità e perché raggiunge il valore
massimo dove il momento è minimo.
VERIFICA ALLO S.L.U. DI INSTABILITÀ FLESSO-TORSIONALE
Verifichiamo ora la possibilità di occorrenza di un’instabilità flessotorsionale (svergolamento).
Dobbiamo determinare il Momento Critico e quindi la Snellezza
Adimensionale.
Lcr = 4.10 m;
EJy (inerzia lungo l’asse debole) = 210000·159000 =3.34·1010;
GJT = 80769·12020 =9.71·108;
EJw = 210000·351·106 =0.74·1014;
ψ = 1.
da ciò si deduce che per il nostro IPE100 sulla luce di 4.10 m:
2
14
π
⎛ π ⎞ 0.74 ⋅ 10
10
8
Mcr = 1 ⋅
3.34 ⋅ 10 ⋅ 9.71 ⋅ 10 ⋅ 1 + ⎜
=
⎟ ⋅
8
4100
⎝ 4100 ⎠ 9.71 ⋅ 10
= 4460197 Nmm = 4.46 KNm
Considerando quindi il modulo di resistenza plastico Wy=39400
mm3:
5
λLT =
39400 ⋅ 235
= 1.44
4460197
Una volta nota la snellezza posso determinare il FATTORE DI
RIDUZIONE DELLA RESISTENZA per effetto dell’instabilità:
con
f tiene conto della reale distribuzione del momento flettente tra i
ritegni torsionali, che non è uniforme e considera un fattore
correttivo kc che si deduce dalla tabella 4.2.VIII delle NTC e in via
approssimata possiamo assumere pari a 0.94.
In definitiva f = 0.99;
λLT,0 può essere assunto per sezioni laminate pari a 0.4;
β può essere assunto per sezioni laminate pari a 0.75;
α LT è il FATTORE DI IMPERFEZIONE riportato nella tab. 4.2.VI delle
NTC, una volta stabilita la curva di instabilità che caratterizza il
nostro profilo. In base alla tab. 4.2.VII si deduce che al nostro
profilo (laminato con H/B≤2) appartiene la curva di instabilità b e
dalla Tab. 4.2.VI deduciamo che α LT =0.34
In definitiva:
Φ LT = 1.45
χ LT = 0.46
La nostra verifica si conclude determinando il momento resistente
di calcolo per i fenomeni di instabilità, pari a:
6
Mb,Rd = χ LT ⋅ Wy ⋅
fyk
γ M1
= 0.46 ⋅ 39400 ⋅
235
= 4056324 Nmm = 4.06 KNm
1.05
Il momento sollecitante complessivo allo SLU era invece:
MEd = 6.83 KNm
La verifica pertanto non è soddisfatta. Peraltro la struttura esistente
sotto esame assume come profilo per gli elementi un IPE160.
Dalla verifica effettuata la lezione precedente è chiaro che data la
luce di 4.10 m e l’entità del momento, probabilmente neanche un
IPE 120 soddisferebbe la verifica, pertanto si proverà adottando un
IPE140.
In tal caso:
H = 140 mm
B = 73 mm
A = 1640 mm2
sa = 4.7 mm
sf = 6.9 mm
Wy = 77300 mm3
Wpl,y = 88300 mm3
Jy = 5412000 mm4
Jz = 449200 mm4
Jt = 24470 mm4
Jw = 1981·106 mm4
ρ = 0.13 KN/m
Lcr = 4.10 m;
EJy = 210000·449200 =9.43·1010;
GJT = 80769·12020 =19.76·108;
EJw = 210000·1981·106 =4.16·1014;
ψ = 1.
7
da ciò si deduce che per il nostro IPE140 sulla luce di 4.10 m:
2
14
π
⎛ π ⎞ 4.16 ⋅ 10
10
8
Mcr = 1 ⋅
9.43 ⋅ 10 ⋅ 19.76 ⋅ 10 ⋅ 1 + ⎜
=
⎟ ⋅
8
4100
⎝ 4100 ⎠ 19.76 ⋅ 10
= 11087211 Nmm = 11.09 KNm
Considerando quindi il modulo di resistenza plastico Wy=39400
mm3:
88300 ⋅ 235
λLT =
= 1.37
11087211
Una volta nota la snellezza posso determinare il FATTORE DI
RIDUZIONE DELLA RESISTENZA per effetto dell’instabilità:
con
kc = 0.94.
f = 0.99;
λLT,0 può essere assunto per sezioni laminate pari a 0.4;
β può essere assunto per sezioni laminate pari a 0.75;
α LT =0.34
In definitiva:
Φ LT = 1.37
χ LT = 0.49
8
La nostra verifica si conclude determinando il momento resistente
di calcolo per i fenomeni di instabilità, pari a:
fyk
235
= 9683566.7 Nmm = 9.68 KNm
γ M1
1.05
che è > di MED= 6.61 +1.3·0.12·4.102/8= 6.94 KN/m.
Mb,Rd = χ LT ⋅ Wy ⋅
= 0.49 ⋅ 88300 ⋅
ULTERIORI ANALISI
Per completezza andiamo a verificare cosa succede nel cavalletto
che costituisce lo shed:
9
VERIFICA DEL MONTANTE
Aggiungiamo la verifica a pressoflessione del montante. Adottando
il metodo elastico, si determina:
MED = 4.91 KN/m
NED = 7.80 KN
TED = 3.09 KN
Comprensivi del peso proprio.
σx,ED=
NED MED
7.80 x 103 4.91 x 106
+
=
+
=68.27 N/mm2 < 235/1.05
A
Wy
1640
77300
Av = A -2b·sf + (sa + 2r) ·sf = 755 mm2
τ y,ED =
VED
3.09 x 1000
=
= 4.09 N/mm2
AV
755
σx,ED2+3τ y,ED2 = (68.27)2 + 3(4.09)2 =4711< (fyk / γ M0 ) = 50091 (OK)
2
Verifichiamo la necessità di una verifica di instabilità del montante
per semplicità solo flessionale:
considerando che il montante è alto 1.80 m e ipotizzando un
vincolo cerniera-cerniera, con traslazioni di estremità impedite
(β=1), la lunghezza libera di inflessione è pari a 1.80 m.
assumendo le proprietà geometriche dell’IPE140 prescelto si ricava
un carico critico pari a:
10
Ncr = 287.35 KN
E la snellezza relativa λ = 1.16 ;
si nota però che NED < 0.04 Ncr = 11.49 KN, pertanto l’effetto
dell’instabilità flessionale può essere trascurato.
Considerazioni finali
Tenuto conto che nella struttura a shed le sollecitazioni sono molto
basse rispetto al caso di elemento semplicemente appoggiato
potrebbe valere la pena di considerare una sezione inferiore, p.e.
un’IPE120 e prevenire l’instabilità con dei ritegni.
11
CORSO DI COSTRUZIONI
IN ACCIAIO
270 Laurea Magistrale
I anno – I semestre
ESERCITAZIONE:
CALCOLO DELLA STRUTTURA DI UN CAPANNONE
INDUSTRIALE SITO NELLA CITTÀ DI CAGLIARI
Parte 4
TITOLARE: Prof. Ing. Barbara De Nicolo
RELATORE: Ing. Daniel Meloni
TRAVE RETICOLARE SECONDARIA
Si procederà ora al dimensionamento e la verifica delle travi
secondarie. Nella struttura esistente questo ruolo è svolto da travi
tipo Vierendel, noi dimensioneremo invece delle travi tipo Pratt.
Le travi in oggetto hanno luce di 12 m e sono impostate sulle travi
principali. Sono divise in tre campi da 4 m dagli shed. Poiché il
carico portato dalle diagonali alle estremità è scaricato direttamente
sulle travi principali, lo schema statico prevede che il carico della
copertura si scarichi ai terzi della trave in modo concentrato in
prossimità dei montanti degli shed.
Assumeremo il seguente schema statico di riferimento.
La realizzazione dello schema unifilare deve sempre tenere conto di
alcune approssimazioni, imposte dal reale ingombro dei profili e
dall’esigenza di far convergere in un punto tutti gli assi concorrenti
in un nodo.
ANALISI DEI CARICHI
Determineremo ora i carichi concentrati agenti sulla trave sotto
esame. Ipotizzeremo che gli shed abbiano un vincolo di semplice
appoggio sul corrente superiore della trave e trascureremo la
reazione orizzontale trasmessa dal diagonale. Determineremo
1
quindi i soli carichi concentrati verticali in base alle reazioni di
appoggio degli arcarecci e il peso di diagonale e montante dello
shed ipotizzando che siano realizzati con profili IPE140.
REAZIONE DEGLI ARCARECCI
reazione di appoggio carico permanente Rp = 0.88 (0.44) KN
reazione di appoggio carico da neve Rn = 0.74 (0.37) KN
reazione di appoggio carico variabile Rv = 0.86 (0.43) KN
PESO DEL DIAGONALE
Pd = 0.13·4.10 = 0.53 KN
PESO DEL MONTANTE
Pm = 0.13·1.70 = 0.22 KN
In definitiva, avremo per la componente permanente:
Pp = 4·Rp+2·Rp/2 + 2·Pd/2 + Pm =5.15 KN
Per il carico da neve:
Pn = 4·Rn+2·Rn/2 =3.70 KN
Per il carico variabile:
Pv = 4·Rv+2·Rv/2 =4.30 KN
pertanto allo stato limite ultimo si potrà porre:
PSLU = 1.3·5.15+1.5(4.30+0.5·3.70) =15.92 KN
MATERIALI
Ipotizzeremo l’uso di profilati laminati a caldo realizzati con acciaio
duttile di grado S235JR conforme alla norma armonizzata UNI EN
10025 (ex Fe360B). Tale materiale è caratterizzato dalle seguenti
proprietà meccaniche:
modulo di elasticità E = 210000 MPa
carico unitario di rottura ftk = 360 MPa
carico unitario di snervamento fyk = 235 MPa
2
PREDIMENSIONAMENTO
Il predimensionamento di una trave reticolare richiede la
determinazione dell’altezza e la scelta del profilo degli elementi, con
particolare attenzione ai correnti inferiore e superiore. Nell’ipotesi di
aver predeterminato l’altezza dell’elemento, magari in funzione di
esigenze architettoniche, si può, in via approssimata ragionare
come segue.
Si può ipotizzare di considerare la trave reticolare come se fosse a
parete piena e determinare la sollecitazione flettente.
Facendo riferimento allo schema statico di cui sopra, in cui P = PSLU
= 15.92 KN ed L = 12 m, trascurando il peso proprio della trave, si
ottiene:
MSLU = PSLU·4.00 = 63.68 KNm
Ipotizzando un’altezza della trave pari a 0.60 m (come nella
struttura esistente) e assimilando a questa misura il braccio delle
forze interne tra la trazione nel corrente inferiore della trave
reticolare e la compressione nel corrente superiore, possiamo
determinare l’entità di queste azioni e quindi attribuire un
predimensionamento agli elementi.
NSLU = MSLU/H = 63.68/0.60 = 106 KN
Quindi l’area minima del profilo con cui realizziamo il corrente
superiore e quello inferiore (in genere uguali) sarà almeno:
Amin = 106·103/(235/1.05)=463.62 mm2
3
Ipotizziamo di utilizzare un profilo a T. In tal caso il profilo
commerciale che mi garantisce tale area resistente sarà un T50.
Consideriamo però anche la deformabilità. Supponiamo di imporre il
limite della freccia a carico totale (a meno del peso proprio), pari a:
flim= L/200 = 12000/200 = 60 mm
sempre ipotizzando un comportamento a parte piena, è noto che in
mezzeria:
fmax=
P⋅a
(3L2 − 4a2 ) = flim= 60 mm
24EJmin
In questo caso P = PSLE = 5.15+4.30+0.5·3.70 =11.30 KN
da cui:
11.30 ⋅ 103 ⋅ 4 ⋅ 103
(3 ⋅ (12.00 ⋅ 103 )2 − 4 ⋅ (4.00 ⋅ 103 )2 ) =5.5·107mm4
Jmin=
24 ⋅ 210000 ⋅ 60
A questo punto, poiché non abbiamo una
sezione a parete piena, ipotizzeremo che la
sezione trasversale della trave reticolare resti
piana e si comporti in modo rigido, ovvero le
aste di parete siano in grado di impedire gli
scorrimenti tra i due correnti inferiore e
superiore. Considereremo quindi la sezione al
lato:
Jmin≈ 2Amin·(d/2)2 ≈ 2Amin·(H/2)2 = 5.5·107 mm4
e Amin = 5.5·107/2·3002= 306 mm2
4
il limite determinato sulla resistenza sembra essere prevalente,
quindi il profilo T50 sembra essere sufficiente. In realtà dobbiamo
considerare l’effetto del peso proprio della struttura che ha un
incidenza di almeno il 10%, l’indebolimento delle sezioni in
corrispondenza delle connessioni e la presenza di azioni flettenti
(che noi trascuriamo). Inoltre abbiamo considerato il braccio delle
forze interne pari all’altezza complessiva della trave, mentre invece
sarà lievemente inferiore. Considereremo pertanto un profilo
superiore il T70 a spigoli vivi, le cui caratteristiche principali sono
riportate di seguito.
H = 70 mm
B = 70 mm
sa = 9 mm
sf = 9 mm
A = 1180 mm2
Jy = 890000 mm4
Jz = 108000 mm4
ρ = 0.09 KN/m
Il profilo ha Classe 1.
Per le aste di parete, considereremo dei profili ad L accoppiati, che
supporremo saldati o imbullonati all’anima dei correnti. In prima
approssimazione considereremo dei profili ad L40x40x4.
Globalmente possiamo stimare quindi un peso proprio della trave
pari a
4.50 KN che potremmo aggiungere alla componente
permanente dei carichi concentrati P, oppure distribuire ai nodi.
5
CALCOLO DELLA TRAVE RETICOLARE
Si ricorda che perchè la trave in esame possa essere calcolata come
elemento reticolare è necessario che sussistano delle condizioni:
1) carichi applicati solo ai nodi;
2) aste mutuamente incernierate;
la prima condizione è sostanzialmente verificata nel nostro caso. La
seconda non lo è in generale mai. Infatti le travi reticolari vengono
quasi sempre assemblate con correnti continui (al più giuntando più
elementi per ragioni di trasporto) e aste di parete connesse ad essi
con saldature o bullonature. Trascurando la valutazione del grado di
vincolo delle aste di parete, è evidente che le briglie superiore ed
inferiore saranno sempre oggetto di azioni flessionali; pertanto
assimilare questi elementi a strutture reticolari è solo
un’approssimazione.
Inoltre perché si possa avere uno schema isostatico è necessario
che:
1) Lo schema sia isostatico esternamente (vincoli a terra);
2) Il numero delle aste dello schema rispetti la relazione:
2n -3 = a
dove n = numero dei nodi
a = numero delle aste
in definitiva per poter effettuare un calcolo a mano della trave in
esame, bisogna approssimarla ad un elemento “strettamente”
reticolare, introducendo delle sconnessioni nei correnti inferiore e
superiore. Spesso neanche i vincoli delle aste di parete possono
realmente essere considerati cerniere, come nel caso dell’uso di
saldature.
Si dimostra che agli effetti dell’analisi strutturale non si commette
un errore eccessivo se si accettano queste approssimazioni.
Quanto all’isostaticità del nostro schema, si ha:
2n-3 = 2 x 26 -3 = 49 = a
6
METODO RISOLUTIVO
Essendo l’elemento isostatico, il problema è risolvibile con le sole
equazioni di equilibrio. Risolvere la struttura significa determinare le
componenti di azione interna di ogni singola asta. Essendo le aste
incernierate, caricate solo ai nodi e rettilinee lo stato di
sollecitazione prevede sole azioni assiali.
Nota che se le aste non fossero rettilinee si avrebbero in generale
anche azioni di taglio e momento.
L’analisi verrà svolta col Metodo dell’equilibrio ai nodi. Ad ogni iesimo nodo, fissato un sistema di riferimento x-y arbitrario, si
imporrà che:
∑Fx = 0
(dalle equazioni cardinali della statica)
∑Fy = 0
Tra le forze genericamente indicate con F si consideranno sia le
componenti di azione interna Fij, sia le forze esterne (carichi esterni
e reazioni vincolari).
Il metodo procede da un nodo all’altro, avendo cura di analizzare i
nodi in ordine tale da avere sempre non più di due incognite (le
azioni nelle aste) per volta.
Si considereranno convenzionalmente positive le trazioni e negative
le compressioni.
RISOLUZIONE
Considereremo lo schema riportato in figura.
7
Attenzione, in via semplificativa, si è considerata l’altezza H della
trave pari a 0.60 m, in realtà lo schema unifilare dovrebbe essere
tracciato con riferimento agli assi baricentrici dei profili utilizzati, e
già predimensionati.
Innanzitutto determiniamo le reazioni di appoggio:
R = 2·P/2 = 15.92 KN
NODO 1
Convenzionalmente partiremo per tutte le incognite con l’ipotesi che
si tratti di azioni di trazione, quindi positive. Se il risultato porgerà
un segno negativo ciò sta a significare che l’ipotesi iniziale era
errata e che l’azione è di compressione.
∑ Fx = F1-3 = 0
∑ Fy = R1+F1-2 = 0
F1-3 = 0
F1-2 = - 15.92 KN (puntone)
NODO 2
∑ Fx = F2-4+F2-3cos(31°) = 0
∑ Fy = F1-2+F2-3sen(31°) = 0
F2-4 = -0.857·F2-3
-15.92+0.514·F2-3 = 0
F2-3 = +30.95 KN (tirante)
F2-4 = - 26.54 KN (puntone)
8
NODO 3
∑ Fx = -F1-3-F2-3cos(31°)+ F3-5 = 0
∑ Fy = F3-4+F2-3sen(31°) = 0
F3-5 = 0+0.857·30.95
F3-4 = -0.514·30.95
F3-5 = 26.53 KN (tirante)
F3-4 = -15.92 KN (puntone)
NODO 4
∑ Fx = -F2-4+F4-5cos(31°)+ F4-6 = 0
∑ Fy = -F3-4-F4-5sen(31°) = 0
F4-6 = -26.53-0.857· F4-5
F4-5 = -15.92/0.514
F4-6 = -53.07 KN (puntone)
F4-5 = +30.94 KN (tirante)
NODO 5
∑ Fx = -F3-5-F4-5cos(31°)+ F5-7 = 0
∑ Fy = F5-6+F4-5sen(31°) = 0
F5-7 = 26.53+0.857·30.94
F5-6 = -30.94·0.514
F5-7 = +53.07 KN (tirante)
F5-6 = -15.92 KN (puntone)
9
NODO 6
∑ Fx = -F4-6-F6-7cos(31°)+ F6-8 = 0
∑ Fy = -F5-6+F6-7sen(31°) = 0
F6-8 = -53.07+0.857· F6-7
F6-7 = -15.92/0.514
F6-8 = -79.59 KN(puntone)
F6-7 = -30.94 KN (tirante)
NODO 7
∑ Fx = -F5-7+F6-7cos(31°)+ F7-9 = 0
∑ Fy = +F7-8-F6-7sen(31°) = 0
F7-9 = 53.07+0.857·30.94
F7-8 = -30.94·0.514
F7-9 = +79.59 KN (tirante)
F7-8 = -15.92 KN (puntone)
NODO 8
∑ Fx = -F6-8+F8-9cos(31°)+ F8-10 = 0
∑ Fy = -F7-8-F8-9sen(31°) = 0
F8-10 = -79.59-0.857· F8-9
F8-9 = 15.92/0.514
F8-10 = -106.13 KN (puntone)
F8-9 = +30.94 KN (tirante)
10
NODO 6
∑ Fx = -F4-6-F6-7cos(31°)+ F6-8 = 0
∑ Fy = -F5-6+F6-7sen(31°) = 0
F6-8 = -53.07+0.857· F6-7
F6-7 = -15.92/0.514
F6-8 = -79.59 KN(puntone)
F6-7 = -30.94 KN (tirante)
NODO 7
∑ Fx = -F5-7+F6-7cos(31°)+ F7-9 = 0
∑ Fy = +F7-8-F6-7sen(31°) = 0
F7-9 = 53.07+0.857·30.94
F7-8 = -30.94·0.514
F7-9 = +79.59 KN (tirante)
F7-8 = -15.92 KN (puntone)
NODO 8
∑ Fx = -F6-8+F8-9cos(31°)+ F8-10 = 0
∑ Fy = -F7-8-F8-9sen(31°) = 0
F8-10 = -79.59-0.857· F8-9
F8-9 = 15.92/0.514
F8-10 = -106.13 KN (puntone)
F8-9 = +30.94 KN (tirante)
11
NODO 9
∑ Fx = -F7-9-F8-9cos(31°)+ F9-11 = 0
∑ Fy = F9-10+F8-9sen(31°) = 0
F9-11 = 79.59+0.857·30.94
F9-10 = -30.94·0.514
F9-11 = 106.13 KN (tirante)
F9-10 = -15.92 KN (puntone)
NODO 10
∑ Fx = -F8-10+F10-11cos(31°)+ F10-12 = 0
∑ Fy = -F9-10-F10-11sen(31°)-P = 0
F10-12 = -106.13+0.857·F10-11
F10-11 = (15.92-15.92)/0.514
F10-12 = -106.13KN (puntone)
F10-11 = 0
NODO 11
∑ Fx = -F9-11+F10-11cos(31°)+F11-13 = 0
∑ Fy = F11-12-F10-11sen(31°) = 0
F11-13 = 106.13 KN (tirante)
F11-12 = 0
12
Il calcolo prosegue, ovviamente in condizioni di simmetria
senza
necessità di andare oltre il nodo 14. Riepiloghiamo di seguito i
risultati ottenuti:
BRIGLIA SUPERIORE
F2-4 = - 26.54 KN (puntone)
F4-6 = -53.07 KN (puntone)
F6-8 = -79.59 KN(puntone)
F8-10 = -106.13 KN (puntone)
F10-12 = -106.13 KN (puntone)
F12-14 = -106.13 KN (puntone)
BRIGLIA INFERIORE
F1-3 = 0
F3-5 = +26.53 KN (tirante)
F5-7 = +53.07 KN (tirante)
F7-9 = +79.59 KN (tirante)
F9-11 = +106.13 KN (tirante)
F11-13 = +106.13 KN (tirante)
MONTANTI
F1-2 = - 15.92 KN (puntone)
F3-4 = -15.92 KN (puntone)
F5-6 = -15.92 KN (puntone)
F7-8 = -15.92 KN (puntone)
F9-10 = -15.92 KN (puntone)
F11-12 = 0
F13-14 = 0
DIAGONALI
F2-3 = +30.94 KN (tirante)
F4-5 = +30.94 KN (tirante)
F6-7 = +30.94 KN (tirante)
F8-9 = +30.94 KN (tirante)
F10-11 = 0
F12-13 = 0
13
Si osserva che effettuando un calcolo più rigoroso, tenendo in conto
la continuità dei correnti superiori ed inferiori (p.e. per mezzo di un
codice FEM), ma mantenendo le cerniere per le aste di parete, si
ottengono i seguenti risultati:
BRIGLIA SUPERIORE
Nmax= - 105.2 KN (-1%)
BRIGLIA INFERIORE
Nmax= + 105 KN (-1%)
MONTANTI
Nmax= - 15.83 KN (-1%)
DIAGONALI
Nmax= 31.00 KN (+0.1%)
Nell’ipotesi di predimensionamento formulata, il modello FEM
consente di mettere in conto in modo molto celere il peso proprio
degli elementi:
BRIGLIA SUPERIORE
Nmax= - 119.4 KN (+12,5%)
BRIGLIA INFERIORE
Nmax= + 119.2 KN (+12,5%)
14
MONTANTI
Nmax= - 18.64 KN (+17%)
DIAGONALI
Nmax= 35.70 KN (+15%)
Come si può notare l’incremento dovuto al peso proprio va dal 12,5
al 17%, il che giustifica il fatto di tenerne conto in forma forfetaria.
Ovviamente dal modello FEM con correnti continui emerge la
presenza di azioni flessionali negli stessi che prima non era
possibile determinare:
L’entità di queste azioni è di 0.93 KNm nel corrente superiore e
0.83 KNm in quello inferiore (tenuto conto anche del peso proprio)
Effettuando un ulteriore calcolo in assenza di cerniere interne,
modellazione che avrebbe un senso in presenza di aste connesse
per mezzo di saldature, si otterrebbe invece:
BRIGLIA SUPERIORE
Nmax= - 119.4 KN (-1%)
BRIGLIA INFERIORE
Nmax= + 119.2 KN (-1%)
MONTANTI
Nmax= - 18.33 KN (-1%)
DIAGONALI
Nmax= 34.60 KN (+0.1%)
Che sono quasi identici ai valori precedenti ma con la differenza che
le aste di parete questa volta sarebbero sottoposte ad un’azione
15
flessionale distribuita linearmente. L’entità di questa azione è però
contenuta, perché la maggior parte di essa si trasmette in ogni
nodo ai correnti, vista la maggiore inerzia flessionale.
VERIFICHE DEGLI ELEMENTI
Procederemo ora alla verifica delle aste, tenuto conto del fatto che
si considererà un unico profilo per ogni tipologia di asta.
CORRENTE SUPERIORE
Il corrente superiore è sottoposto ad un’azione assiale che
raggiunge il massimo nei campi centrali ed un’azione flessionale
indotta dalla sua continuità. Allo Stato Limite Ultimo, considerando
anche il peso proprio:
NED= - 119.4 KN
MED= 0.93 KNm
VED= 1.04 KN
Abbiamo considerato il seguente profilo:
H = 70 mm
B = 70 mm
sa = 9 mm
sf = 9 mm
A = 1180 mm2
Wy = 25514.4 mm3
Jz = 108000 mm4
Jy = 890000 mm4
ρ = 0.09 KN/m
Il profilo ha Classe 1.
16
Effettuiamo la verifica a pressoflessione:
σx,ED=
NED MED
+
A
Wy
=
119.4 x 103 0.93 x 106
+
=101.20+36.45=137.65
1180
25514
N/mm2 < 235/1.05
Av = 630 mm2
τ y,ED =
VED
1.04 x 1000
=
= 1.65 N/mm2
AV
630
σx,ED2+3τ y,ED2=(137.65)2+3(1.65)2= 18955< (fyk / γ M0 ) =50091 (OK)
2
verifichiamo l’instabilità flessionale nel piano verticale (asse forte):
lunghezza dell’asta L= 1.00 m
coerentemente con lo schema reticolare che ha generato l’azione, la
lunghezza libera di inflessione corrisponde alla lunghezza
dell’elemento, quindi:
lunghezza libera di inflessione L0 = L = 1.00 m
determiniamo il carico critico elastico:
Ncr =
π 2 ⋅ E ⋅ Jy
l0
2
=
π 2 ⋅ 210000 ⋅ 890000
= 1844629 N = 1844.6 KN
10002
Determiniamo la snellezza relativa:
λ=
A ⋅ fyk
Ncr
=
1180 ⋅ 235
= 0.39 > 0.20
1844629
Nota inoltre che NED > 0.04 Ncr
Quindi, secondo le indicazioni delle NTC l’instabilità rispetto all’asse
forte (nel piano della trave reticolare) non può essere trascurata.
17
Per procedere alla verifica dobbiamo determinare il fattore di
riduzione χ:
con
α è il FATTORE DI IMPERFEZIONE riportato nella tab. 4.2.VI delle
NTC, una volta stabilita la curva di instabilità che caratterizza il
nostro profilo. Alle sezioni a T, compete la curva di instabilità c e
dalla Tab. 4.2.VI deduciamo che α =0.49, da cui:
Φ = 0.62 Æ χ = 0.90
Quindi dobbiamo effettuare la verifica:
NbRD =
χ ⋅ A ⋅ fyk
γ M1
=
0.90 ⋅ 1180 ⋅ 2350
= 238688 N= 238.7 KN > NED
1.05
Per quanto riguarda l’instabilità flessionale fuori dal piano della
trave, si fanno le seguenti osservazioni:
1) Le aste di parete non sono in grado di offrire un efficace ritegno
allo sbandamento del corrente superiore, perché poco rigide e
comunque incernierate. Ne consegue che la lunghezza libera di
inflessione del corrente corrisponde alla sua intera lunghezza (12
m!!). È pertanto evidente che la verifica di instabilità in questa
direzione sarà sempre negativa;
2) Non è pensabile di provvedere adottando
sufficientemente rigido lungo l’asse debole,
porterebbe a dimensionamenti antieconomici;
un profilo
perché ciò
3) L’unica soluzione è impedire lo sbandamento del corrente con dei
ritegni. Spesso le strutture cui il profilo è collegato (p.e. ordito
18
secondario, arcarecci) sono in grado di spezzare la luce di
inflessione, consentendo di ridurla a valori accettabili per la
verifica;
4) Nel nostro caso la situazione non è molto favorevole per la
presenza degli elementi di shed, che non appaiono in grado di
fornire un sicuro ritegno. Sarà necessario immaginare altre
soluzioni, per esempio la predisposizione di appositi controventi
di piano, come si vedrà in seguito.
CORRENTE INFERIORE
NED= - 119.2 KN
MED= 0.83 KNm
VED= 0.90 KN
Effettuiamo la verifica a tensoflessione:
N
M
σx,ED= ED + ED
A
Wy
119.2 x 103 0.83 x 106
+
=
=101.02+32.535=133.55
1180
25514
N/mm2 < 235/1.05
Av = 630 mm2
τ y,ED =
VED
0.90 x 1000
=
= 1.43 N/mm2
AV
630
σx,ED2+3τ y,ED2 =(133.55)2+3(1.43)2 =17842< (fyk / γ M0 ) = 50091 (OK)
2
19
MONTANTI
NED= - 18.64 KN
Consideriamo il seguente profilo:
L = 40 mm
s = 4 mm
A = 308 mm2
W = 1550 mm3
J = 44700 mm4
ρ = 0.024 KN/m
Abbiamo supposto di accoppiare due di questi profili in modo
simmetrico e saldarli o imbullonarli all’anima del T.
Questa configurazione permette di trascurare eventuali eccentricità
dell’azione assiale che avrebbero costretto a considerare una
sezione resistente ridotta.
Facciamo la verifica a compressione:
NED 18.93 x 103
=
=30.73 N/mm2 < 235/1.05
σx,ED=
A
308 ⋅ 2
verifichiamo l’instabilità flessionale:
lunghezza dell’asta L~ 0.60 m
lunghezza libera di inflessione L0 = L = 0.60 m
determiniamo il carico critico elastico:
Ncr =
π 2 ⋅ E ⋅ J π 2 ⋅ 210000 ⋅ 44700
=
= 257350 N = 257.4 KN
2
6002
l0
Determiniamo la snellezza relativa:
20
λ=
A ⋅ fyk
Ncr
=
308 ⋅ 235
= 0.53
257350
e NED > 0.04Ncr = 10.28 KN
L’instabilità non può essere trascurata, a meno che non accoppiamo
in qualche modo i due profili in modo che restino solidali (p.e. con
imbottiture).
Per procedere alla verifica dobbiamo determinare il fattore di
riduzione χ:
con
α è il FATTORE DI IMPERFEZIONE riportato nella tab. 4.2.VI delle
NTC, una volta stabilita la curva di instabilità che caratterizza il
nostro profilo. Alle sezioni ad L, compete la curva di instabilità b e
dalla Tab. 4.2.VI deduciamo che α =0.34, da cui:
Φ = 0.70 Æ χ = 0.87
Quindi dobbiamo effettuare la verifica:
NbRD =
χ ⋅ A ⋅ fyk
γ M1
=
0.87 ⋅ 308 ⋅ 2350
= 60008 N= 60 KN > NED/2
1.05
21
DIAGONALI
NED= 35.70 KN
Considereremo lo stesso profilo ad L
accoppiato, già utilizzato per i montanti:
L = 40 mm
s = 4 mm
A = 308 mm2
W = 1550 mm3
J = 44700 mm4
ρ = 0.024 KN/m
σx,ED
NED 35.70 x 103
=
=
=57.95 N/mm2 < 235/1.05
308 ⋅ 2
A
VERIFICA ALLO SLE DI DEFORMABILITÀ
Per celerità la freccia della trave è stata determinata sulla base del
modello FEM. Assumendo i soliti limiti già considerati per gli
arcarecci, si ha:
δmax = freccia dovuta al carico totale = L/200
δ2 = freccia dovuta al solo carico variabile = L/250
Dal modello si evince che:
δmax = 12.36 < L/200 = 60 mm
δ2 = < 6.72 L/250 = 48 mm
OSSERVAZIONI FINALI
Dalle verifiche si osserva che le aste, soprattutto quelle di parete,
sono state sovradimensionate, quindi si potrebbe ragionare su una
loro ottimizzazione.
22
CORSO DI COSTRUZIONI
IN ACCIAIO
270 Laurea Magistrale
I anno – I semestre
ESERCITAZIONE:
CALCOLO DELLA STRUTTURA DI UN CAPANNONE
INDUSTRIALE SITO NELLA CITTÀ DI CAGLIARI
Parte 5
TITOLARE: Prof. Ing. Barbara De Nicolo
RELATORE: Ing. Daniel Meloni
TRAVE RETICOLARE PRIMARIA
Si procederà ora al dimensionamento e la verifica della trave
primaria, di tipo Pratt, mostrata di seguito.
Le travi in oggetto hanno luce di 24 m e altezza complessiva di 2.40
m. Sono impostate sui pilastri disposti a maglia 24x12 m e
supportano quelle secondarie, connesse ad esse ogni 4 metri,
corrispondenti a due dei campi da 2 m in cui è scandita la trave. La
sezione trasversale è costituita come mostrato nell’immagine che
segue, in cui sono mostrati gli elementi utilizzati nella struttura
esistente di riferimento.
1
La realizzazione dello schema unifilare risente delle medesime
avvertenze già discusse in precedenza e pertanto si potrà fare
riferimento al seguente schema reticolare.
Il dettaglio del collegamento tra la trave secondaria e quella
primaria è ovviamente più complesso nella realtà, ma data la
rigidezza dell’estremità della trave secondaria indotta dal pannello
saldato tra i correnti, la schematizzazione da noi adottata, che
prevede di appendere la trave secondaria in corrispondenza dei
montanti, può considerarsi attendibile. Anche rispetto allo schema
adottato nella lezione precedente (trave Pratt, anziché Vierendel)
tale approssimazione non produrrà pesanti ripercussioni sulla
progettazione degli elementi della trave principale.
2
ANALISI DEI CARICHI
I carichi concentrati applicati ai nodi della trave principale possono
essere dedotti a partire dall’analisi delle reazioni di appoggio della
trave secondaria per quanto riguarda i nodi del corrente inferiore,
mentre per quanto attiene ai carichi applicati al corrente superiore
questi sono indotti dal diagonale degli shed che appoggia
direttamente su di essi scaricando il carico di alcuni arcarecci. In
realtà sul corrente della trave agisce anche il peso dell’infisso
direttamente impostato su di esso, ma data la sua leggerezza è
consentito tralasciarne la presenza.
REAZIONI TRAVE SECONDARIA
reazione di appoggio allo SLU RSLU = 18.84 KN (compreso p.p.)
reazione di appoggio allo SLE RSLE = 11.30 KN (escluso p.p.)
REAZIONE DI APPOGGIO DEI DIAGONALI
Pd = 0.13·4.10 = 0.53 KN
3
Assumiamo che ogni diagonale scarichi in appoggio il carico di
competenza di 3 arcarecci, di cui uno di estremità (il carico è circa
la metà degli altri).
reazione di appoggio carico permanente Rp = 0.88 (0.44) KN
reazione di appoggio carico da neve Rn = 0.74 (0.37) KN
reazione di appoggio carico variabile Rv = 0.86 (0.43) KN
In definitiva, avremo per la componente permanente:
Pp = 4·Rp+2·Rp/2 + 2·Pd/2 =4.93 KN
Per il carico da neve:
Pn = 4·Rn+2·Rn/2 =3.70 KN
Per il carico variabile:
Pv = 4·Rv+2·Rv/2 =4.30 KN
In definitiva, considerando una trave primaria intermedia, si avrà:
PSLU = 2· RSLU =37.70 KN (carichi appesi)
P’SLU = 1.3·Pp+1.5·(Pv+0.5·Pn)= 15.63 KN
MATERIALI
Ipotizzeremo l’uso di profilati laminati a caldo realizzati con acciaio
duttile di grado S235JR conforme alla norma armonizzata UNI EN
10025 (ex Fe360B). Tale materiale è caratterizzato dalle seguenti
proprietà meccaniche:
modulo di elasticità E = 210000 MPa
carico unitario di rottura ftk = 360 MPa
carico unitario di snervamento fyk = 235 MPa
4
PREDIMENSIONAMENTO
Il predimensionamento degli elementi può essere condotto come in
precedenza trattando la reticolare come una comune trave
appoggiata e determinando la coppia interna corrispondente alla
massima azione flettente in mezzeria. Si ricorderà che in genere un
predimensionamento a resistenza è sufficiente.
Supponiamo di aver selezionato i seguenti profili:
CORRENTE INFERIORE E SUPERIORE
2xUPN140
H = 140 mm
B = 60 mm
sa = 7 mm
sf = 10 mm
A = 2040 mm2
Wy = 86400 mm3
Jy = 6050000 mm4
Jz = 627000 mm4
ρ = 0.16 KN/m
Il profilo ha Classe 1.
MONTANTE
2xUPN80
H = 80 mm
B = 45 mm
sa = 6 mm
sf = 8 mm
A = 1100 mm2
Jy = 1060000 mm4
Jz = 194000 mm4
ρ = 0.09 KN/m
Il profilo ha Classe 1.
5
DIAGONALE
PIATTO 80X45 mm
H = 45 mm
B = 80 mm
A = 3600 mm2
Jy = 607500 mm4
Jz = 1920000 mm4
ρ = 0.28 KN/m
Il profilo ha Classe 1.
CALCOLO DELLA TRAVE RETICOLARE
La trave a seguito della nostra schematizzazione è a tutti gli effetti
una trave reticolare isostatica, pertanto potrò essere risolta coi
metodi consueti, tra cui l’equilibrio ai nodi come fatto in precedenza
per le travi secondarie. Lo schema di riferimento è, quindi, il
seguente.
6
Di seguito sono riportati i risultati ottenuti a seguito dell’analisi (per
comodità condotta con un codice FEM), relativi alla combinazione
allo SLU prescelta e comprensivi di peso proprio:
BRIGLIA SUPERIORE
F2-4 = -253.43 KN
F4-6 = -461.33 KN
F6-8 = -622.91 KN
F8-10 = -783.33 KN
F10-12 = -807.67 KN
F12-14 = -820.63 KN
BRIGLIA INFERIORE
F1-3 = 0
F3-5 = +253.43 KN
F5-7 = +461.33 KN
F7-9 = +622.91 KN
F9-11 = +783.33 KN
F11-13 = +807.67 KN
MONTANTI
F1-2 = - 321.36 KN
F3-4 = -265.97 KN
F5-6 = -210.85 KN
F7-8 = -155.38 KN
F9-10 = -100 KN
7
F11-12 = -44.54 KN
F13-14 = -16.54 KN
DIAGONALI
F2-3 = +396.08 KN
F4-5 = +324.95 KN
F6-7 = +252.60 KN
F8-9 = +180.49 KN
F10-11 = +108.52 KN
F12-13 = +36.08 KN
Si fa notare che l’incidenza del peso proprio sull’entità delle
suddette azioni è di circa il 4%, quindi come rilevato già in
precedenza nel calcolo può essere trascurato per analisi speditive.
Di seguito sono riportati i diagrammi delle azioni assiale, flessionale
e tagliante del modello realizzato con la continuità delle briglie.
Ovviamente l’azione flessionale nelle aste di parete è dovuta
esclusivamente al peso proprio. Come al solito si può dimostrare
che la reticolare ideale porge valori molto simili delle azioni assiali.
8
VERIFICHE DEGLI ELEMENTI
Procederemo ora alla verifica delle aste, tenuto conto del fatto che
si considererà un unico profilo per ogni tipologia di asta.
CORRENTE SUPERIORE
Il corrente superiore è sottoposto ad un’azione assiale che
raggiunge il massimo nei campi centrali ed un’azione flessionale
indotta dalla sua continuità. Allo Stato Limite Ultimo, considerando
anche il peso proprio, nelle aste centrali abbiamo:
NED= - 820.63 KN
MED= 2.60 KNm
VED= 0.40 KN
Abbiamo considerato il seguente profilo composto:
Effettuiamo la verifica a pressoflessione e taglio:
N
M
σx,ED= ED + ED
A
Wy
820.63 x 103 2.60 x 106
+
=
=
2040 ⋅ 2
2 ⋅ 86400
216.18
N/mm2
<
235/1.05
Av = 1040 mm2
τ y,ED =
VED
0.40 x 1000
=
= 0.19 N/mm2
AV
2 ⋅ 1040
9
σx,ED2+3τ y,ED2=(216.18)2+3(0.19)2= 46691< (fyk / γ M0 ) =50091 (OK)
2
verifichiamo l’instabilità flessionale nel piano verticale (asse forte),
considerando il singolo profilo:
lunghezza dell’asta L= 2.00 m
lunghezza libera di inflessione L0 = L = 2.00 m
determiniamo il carico critico elastico:
Ncr =
π 2 ⋅ E ⋅ Jy
l0
2
= 3134833 N = 3134.83 KN
Determiniamo la snellezza relativa:
λ=
A ⋅ fyk
Ncr
=
2040 ⋅ 235
= 0.39
3134833
Dobbiamo determinare il fattore di riduzione χ:
con
α è il FATTORE DI IMPERFEZIONE riportato nella tab. 4.2.VI delle
NTC, una volta stabilita la curva di instabilità che caratterizza il
nostro profilo. Alle sezioni ad C, compete la curva di instabilità b e
dalla Tab. 4.2.VI deduciamo che α =0.49, da cui:
Φ = 0.62 Æ χ = 0.90
Quindi dobbiamo effettuare la verifica:
NbRD =
χ ⋅ A ⋅ fyk
γ M1
=
0.90 ⋅ 2 ⋅ 2040 ⋅ 235
= 823690 N = 823.69 KN > NED
1.05
10
Per quanto riguarda l’instabilità flessionale fuori dal piano della
trave, l’unica soluzione è impedire lo sbandamento del corrente con
dei ritegni. Spesso le strutture cui il profilo è collegato (p.e. ordito
secondario, arcarecci) sono in grado di spezzare la luce di
inflessione, consentendo di ridurla a valori accettabili per la verifica.
in effetti questa funzione potrebbe essere in parte svolta dai
diagonali degli shed, imbullonati al corrente. Il passo di questi
elementi è però di 4.00 m, quindi la lunghezza libera di inflessione
dovrebbe essere valutata a partire da questa misura.
Verifichiamo cosa succede alla verifica considerando l’asta isolata:
lunghezza dell’asta L= 4.00 m
lunghezza libera di inflessione L0 = 4.00 m
determiniamo il carico critico elastico:
π 2 ⋅ E ⋅ Jz
Ncr =
= 81221 N = 81.22 KN
2
l0
Determiniamo la snellezza relativa:
λ=
A ⋅ fyk
Ncr
=
2040 ⋅ 235
= 2.43
81221
Si noti che la snellezza:
λ=
l0
4000
=
= 228 > 200
iz
627000
2040
supera i limiti consigliati per le membrature principali
Dobbiamo determinare il fattore di riduzione χ:
11
con
α è il FATTORE DI IMPERFEZIONE riportato nella tab. 4.2.VI delle
NTC, una volta stabilita la curva di instabilità che caratterizza il
nostro profilo. Alle sezioni ad C, compete la curva di instabilità c e
dalla Tab. 4.2.VI deduciamo che α =0.49, da cui:
Φ = 4.00 Æ χ = 0.14 !!!
Quindi dobbiamo effettuare la verifica:
NbRD =
χ ⋅ A ⋅ fyk
γ M1
=
0.14 ⋅ 2 ⋅ 2040 ⋅ 235
= 127322 N= 127.3 KN <<< NED
1.05
Quindi il fatto di aver accoppiato i profili non ci ha portato alcun
vantaggio rispetto alla verifica di instabilità. Il modo più efficace ed
economico per risolvere il problema è quello di solidarizzare le aste
in modo da indurre un comportamento analogo a quello di un unico
profilo. Questo può avvenire attraverso calastrellature o
imbottiture. Nel caso reale in esame questo effetto è stato ottenuto
tramite piastre di collegamento saldate (calastrelli).
12
In tal caso Jz =21204800 mm4, quindi:
Ncr =
π 2 ⋅ E ⋅ Jz
= 2746839 N = 2746.84 KN
2
l0
Determiniamo la snellezza relativa:
A ⋅ fyk
λ=
= 0.59
Ncr
α =0.49, da cui: Φ = 0.77 Æ χ = 0.79
NbRD =
χ ⋅ A ⋅ fyk
γ M1
=
0.79 ⋅ 2 ⋅ 2040 ⋅ 235
= 722130 N= 722 KN < NED
1.05
La verifica è ancora negativa, ma di poco. A questo punto
scegliendo un profilo superiore la verifica sarà certamente positiva.
13
CORRENTE INFERIORE
NED= - 807.67 KN
MED= 2.60 KNm
VED= 0.40 KN
Effettuiamo la verifica a tensoflessione:
σx,ED=
NED MED
+
A
Wy
=
807.7 x 103 2.60 x 106
+
=
2040 ⋅ 2
2 ⋅ 86400
213.01
N/mm2
<
235/1.05
Av = 1040 mm2
τ y,ED =
VED
0.40 x 1000
=
= 0.19 N/mm2
AV
2 ⋅ 1040
σx,ED2+3τy,ED2=(213.01)2+3(0.19)2=45373.4< (fyk / γ M0 ) = 50091 (OK)
2
14
MONTANTI
NED= - 321.36 KN
Abbiamo supposto di saldare due profili UPN80 in modo simmetrico
e saldarli alle anime degli UPN140. Questo può avvenire nei due
modi mostrati in figura, senza che emergano problemi di
eccentricità delle azioni rispetto agli assi degli elementi.
Facciamo la verifica a compressione:
σx,ED=
NED 321.36 x 103
=
=146.07 N/mm2 < 235/1.05
A
1100 ⋅ 2
verifichiamo l’instabilità flessionale, considerando la seconda
configurazione di accoppiamento; in tal caso Jmin = 742880 mm4:
lunghezza dell’asta L~ 2.40 m
lunghezza libera di inflessione L0 = L = 2.40 m
determiniamo il carico critico elastico e la snellezza relativa:
π2 ⋅ E ⋅ J
= 267310 N = 267.310 KN
Ncr =
2
l0
λ=
A ⋅ fyk
Ncr
= = 1.39
15
α =0.34, da cui: Φ = 1.67 Æ χ = 0.39
Quindi dobbiamo effettuare la verifica:
NbRD =
χ ⋅ A ⋅ fyk
γ M1
=
0.39 ⋅ 2 ⋅ 1100 ⋅ 235
= 190000 N= 190 KN < NED
1.05
Questa modalità di accoppiamento non si è rivelata vantaggiosa
perché non ottimizza l’inerzia dell’asta composta e quindi della sua
snellezza.
Accoppiando secondo la prima configurazione si verifica che l’inerzia
è tale da rendere positiva la verifica, perché in tal caso Jmin =
2364203 mm4 , cui corrisponde NbRD = 363 KN > NED.
Si nota che nella struttura reale sono state adottate entrambe le
configurazioni, la prima con maggiore inerzia nelle aste di parete di
estremità, maggiormente sollecitate.
DIAGONALI
NED= 396.08 KN
La sezioni considerate sono piatti di sezione 80x25 e 80x45. Questi
ultimi utilizzati per le aste diagonali di estremità.
H = 45 mm
B = 80 mm
A = 3600 mm2
Jy = 607500 mm4
Jz = 1920000 mm4
ρ = 0.28 KN/m
Il profilo ha Classe 1.
σx,ED
NED 396.08 x 103
=
=
= 110.02 N/mm2 < 235/1.05
3600
A
16
VERIFICA ALLO SLE DI DEFORMABILITÀ
Per celerità la freccia della trave è stata determinata sulla base del
modello FEM. Assumendo i soliti limiti già considerati per gli
arcarecci, si ha:
δmax = freccia dovuta al carico totale = L/200
δ2 = freccia dovuta al solo carico variabile = L/250
dal modello si evince che:
δmax = 51 < L/200 = 120 mm
δ2 = 32 < 6.72 L/250 = 96 mm
17
CORSO DI COSTRUZIONI
IN ACCIAIO
270 Laurea Magistrale
I anno – I semestre
ESERCITAZIONE:
CALCOLO DELLA STRUTTURA DI UN CAPANNONE
INDUSTRIALE SITO NELLA CITTÀ DI CAGLIARI
Parte 6
TITOLARE: Prof. Ing. Barbara De Nicolo
RELATORE: Ing. Daniel Meloni
CONTROVENTAMENTO
Le
strutture
metalliche
necessitano
quasi
sempre
di
controventamenti, ovvero sistemi in grado di contenere le
deformazioni orizzontali dei telai e degli elementi strutturali.
A differenza delle strutture in c.a. quelle in acciaio o legno, per
motivi economici legati al trasporto e la velocità di montaggio, sono
sempre a ridotto grado di iperstaticità; talvolta i telai, senza
adeguati controventamenti possono anche essere labili.
I motivi per predisporre elementi di controventamento sono:
- stabilizzazione di telai e falde rispetto alle azioni orizzontali
(sisma, vento, apparecchi di sollevamento e trasporto, azioni
instabilizzanti per carichi verticali fuori asse);
- ritegno di elementi soggetti ad instabilità flessionale e torsionale
(travi, correnti di capriate);
- contenimento delle deformazioni orizzontali (SLE di deformabilità
globale).
Il controventamento può essere ottenuto, soprattutto negli edifici in
acciaio multipiano, con nuclei ascensore o vani scala, oltre che con
muri di controvento in c.a.; in tali casi i solai di piano in grado di
fungere da diaframma rigido, rimandano le azioni orizzontali a
questi elementi di per sé dotati di rigidezza a flessione e taglio e
opportunamente verificati (vedi figura seguente). Un caso
particolare è quello delle strutture a orizzontamenti sospesi.
1
Nel caso degli edifici a pochi piani, e sempre in quelli industriali,
l’azione controventante è delegata ad opportuni sistemi di aste.
I controventi convogliano alle fondazioni le azioni orizzontali agenti
sulla struttura in elevazione. Poiché si tratta di strutture non diffuse
ma concentrate in alcuni punti specifici (in genere sono collocati
dentro i telai perimetrali) è però necessario che le azioni orizzontali
vengano prima convogliate ad essi. Spesso sono i solai intermedi e
di copertura, se sufficientemente rigidi nel loro piano, a riportare ai
controventi le azioni orizzontali. In assenza di solai rigidi bisognerà
provvedere con ulteriori controventamenti.
2
Si distinguono quindi:
- CONTROVENTI VERTICALI:
riportano le azioni orizzontali alle fondazioni;
- CONTROVENTI DI PIANO O DI FALDA:
riportano le azioni orizzontali ai controventi verticali;
- CROCIERE ROMPITRATTA:
stabilizzano i correnti compressi di travi e capriate.
3
In riferimento ai controventi verticali, questi possono essere:
CONCENTRICI: del tipo a diagonale tesa attiva, a “V”, a “K”.
ECCENTRICI
4
La scelta del tipo di controventamento deve tenere conto anche
delle diverse capacità dissipative di tali sistemi, rispetto alle azioni
orizzontali cicliche come quella sismica. Nell’ingegneria sismica per
le strutture in acciaio, grande attenzione viene posta sui
meccanismi di collasso dei telai controventati e lo studio della
capacità dissipativa e la duttilità degli stessi. Per esempio i
controventi a “K” poiché la plasticizzazione può avvenire nella
colonna, non sono considerati dissipativi. I controventi a diagonale
tesa o a “K” possono essere dissipativi per plasticizzazione delle
aste tese o in stabilizzazione di quelle compresse. Nei controventi
eccentrici la dissipazione avviene per azione flessionale e tagliante
nel traverso in un tratto detto “link”.
Un telaio verticale iperstatico si definisce controventato quando il
sistema di controventamento è tanto rigido da assorbire il 100%
dell’azione orizzontale di pertinenza. È efficacemente controventato,
se il controvento è in grado di ridurre di almeno l’80% lo
spostamento che il telaio avrebbe in sua assenza.
5
Un telaio efficacemente controventato può considerarsi a nodi fissi
e l’intera azione orizzontale è delegata al controvento, inoltre sono
scongiurati eventuali fenomeni di instabilità globale del telaio.
Un’avvertenza sulla disposizione in pianta dei controventi verticali
richiede che sia assicurata alla struttura adeguata rigidezza
torsionale, poiché sia l’azione sismica che il vento possono produrre
torsioni dell’edificio (p.e. per effetto dell’eccentricità tra il baricentro
delle masse e quello delle rigidezze). In tal caso è necessario che i
controventi non convergano in un punto, diversamente si
assicurerebbe l’esistenza di un centro istantaneo di rotazione e
quindi di una labilità in pianta.
6
REALIZZAZIONE
Gli elementi di controventamento sono aste semplici, in genere
facenti parte di uno schema reticolare. Per ottimizzarne l’utilizzo
sarebbe meglio che tali elementi lavorassero con sole azioni assiali
(maggiore rigidezza) di trazione (nessun rischio di instabilità).
Pertanto in linea di massima si tratterà di elementi incernierati. Si
utilizzerà qualsiasi tipo di profilo adatto alla realizzazione di tiranti:
doppi angolari, doppi UPN, profili tubolari, cavi o a sezione piena.
7
8
LIMITAZIONI DEGLI SPOSTAMENTI LATERALI E GLI
EFFETTI DELLE IMPERFEZIONI
Come sottolineato, la presenza dei controventi è spesso necessaria,
anche laddove i telai siano iperstatici, per la limitazione degli
spostamenti laterali della struttura sotto l’effetto delle azioni
orizzontali. Si tenga presente che tra le azioni si devono
considerare anche quelle fittizie legate alle imperfezioni come i
difetti di verticalità delle colonne dei telai.
Il difetto di verticalità si prende in conto ipotizzando un angolo di
“fuori piombo” convenzionale φ, che poi fa scaturire delle azioni
orizzontali del tipo φQi, ovvero una quota dei carichi verticali agenti
(vedi figura).
La norma, nella Circolare, indica i valori convenzionali che possono
essere adottati a partire da un valore di base pari a H/200, con H =
altezza della struttura.
Si noti che tali effetti possono essere trascurati, secondo le NTC, se
per ogni piano vale:
HEd ≥ 0.15QEd
dove HEd è l’azione orizzontale pertinente a quel piano, valutata
come taglio di piano = sommatoria dei tagli alla base delle colonne
verticale complessivo, anch’esso valutato
e QEd è il carico
9
sommando le azioni alla base delle colonne. In sostanza si
trascurano questi effetti in presenza di azioni orizzontali
considerevoli rispetto a quelle verticali (superiori al 15%).
Gli spostamenti orizzontali delle strutture devono essere
debitamente limitati per le solite ragioni legate al comfort,
all’integrità e funzionalità degli elementi portati e per tutte le
conseguenze negative indotte da un eccesso di spostamento.
Si ricorda a tale proposito che un eccesso di spostamento laterale
può rendere necessario tener conto degli effetti del secondo
ordine indotti dai carichi verticali sull’entità delle sollecitazioni, i
fenomeni di instabilità, ecc. La norma stabilisce i limiti entro i quali
un’analisi globale del primo ordine (equilibrio riferito alla
configurazione in deformata) è sufficiente e non è necessario
procedere oltre.
La limitazione degli spostamenti orizzontali del singolo telaio o
dell’intero edificio è espressa in genere come frazione dell’altezza
dell’edificio o delle singole colonne (∆ spostamento globale, δ
spostamento di interpiano). Alcune indicazioni possono essere
rintracciate nella tab. XI fornita dalle NTC.
10
SCHEMI STRUTTURALI
In linea di massima i sistemi di controventamento sono di tipo
reticolare. Sia i controventi verticali che quelli di piano/falda
possono essere ricondotti a strutture reticolari isostatiche,
sottoposte a carichi corrispondenti alle azioni orizzontali da
contrastare. Se si utilizzano profili molto snelli (p.e. cavi) bisogna
tener presente che a seconda del segno della sollecitazione
dovranno essere presi in conto solo gli elementi sottoposti a
trazione.
Le azioni orizzontali agenti nel piano in una determinata direzione,
prodotte dall’azione sismica (si considera sempre agente alla quota
dei solai di piano e di copertura), dal vento o dall’instabilità delle
travi, sono delegate ad un certo numero di sistemi controventanti.
Questi funzionano come travi reticolari i cui correnti e i montanti
sono in genere rappresentati dall’orditura del piano (primaria o
secondaria), mentre le aste di parete diagonali sono costituite da
aste appositamente dimensionate. Le reazioni di appoggio di tale
trave vanno a scaricarsi sui telai di controvento verticali perimetrali
o intermedi.
11
AZIONI PER INSTABILITÀ DI ASTE E DIFETTI LOCALI
Come visto per i correnti compressi delle travi reticolari di
copertura, l’instabilità fuori dal piano deve essere contrastata da
specifici elementi di ritegno (crociere rompitratta), perché sarebbe
antieconomico pensare di dotare tali elementi di sufficiente inerzia
per superare la verifica di instabilità, tenuto conto che la lunghezza
libera di inflessione corrisponde in genere all’intera luce della trave.
L’EC3 e le NTC (nella Circolare) forniscono la possibilità di
determinare un carico equivalente alla instabilità, a partire dalla
deformazione flessionale che il corrente subirebbe e tenendo conto
dell’eventuale imperfezione di rettilineità dell’asta (difetti locali):
Posti:
NEd = azione di compressione nel corrente da stabilizzare, supposta
uniformemente distribuita, ovvero MEd/h nel caso di travi
inflesse la cui piattabanda deve essere stabilizzata;
e0 =
αm500/L = scostamento
controventato, con:
dalla
rettilineità
dell’elemento
L = luce dell’elemento di controvento;
1 
1
αm =
⋅ 1 +  ;
2 
m
m = numero elementi controventati (il sistema di
controvento
in
genere
stabilizza
più
membrature
contemporaneamente);
12
si può considerare un carico uniformemente distribuito equivalente
qd, dato dall’espressione:
qd =
8 ⋅ (e0 + δ d ) ⋅ NEd
L2
δd = freccia del sistema di controvento dovuta a tutti i carichi.
Nel nostro caso avevamo il problema della stabilizzazione del
corrente superiore delle travi secondarie, non adeguatamente
ritenuto lateralmente. Possiamo allora disporre un sistema di cavi di
controventamento, che vincola i correnti superiori della trave
secondaria, siffatto:
Si può determinare in base all’azione assiale massima portata dal
corrente superiore compresso (N=119.4 KN), il carico equivalente
qd, da applicare sul sistema di controventamento, secondo lo
schema semplificato, eventualmente ponendo δd=0.
13
CALCOLO DEI CONTROVENTI NEL CAPANNONE
Nel caso del nostro capannone, il vincolo al piede dei pilastri è di
incastro. Ma andando ad applicare le azioni orizzontali determinate
(vento, o sisma), si verificherebbe che lo schema a mensola dei
pilastri indurrebbe sollecitazioni flessionali, critiche per gli stessi. È
più vantaggioso, anche per contenere gli spostamenti orizzontali,
predisporre un opportuno schema di controventamento della
struttura, costituito da controventi di falda e controventi verticali.
Diversi sono gli schemi possibili, uno è riportato di seguito:
14
Come si può osservare vi è un sistema di controventi di falda
trasversali che raccoglie le azioni orizzontali longitudinali e li
trasmette
ai
controventi
verticali
longitudinali,
disposti
perimetralmente.
Vi è poi un sistema di controventi di falda longitudinali che
trasmettono le azioni orizzontali trasversali ai controventi verticali
trasversali.
Si supporrà, in base alle indicazioni della tab.4.2.XI, che il limite
massimo tollerato per lo spostamento orizzontale dell’edificio sia
H/150 = 7500/150 = 50 mm.
Benché l’edificio sia ad un solo piano e i carichi verticali non siano
elevati si dovranno tenere in debito conto
gli effetti delle
imperfezioni sull’analisi globale, perché anche le azioni orizzontali
non sono di entità elevata (cioè non è verificato che HEd ≥ 0.15QEd).
Con riferimento all’AZIONE SISMICA avevamo determinato:
Fh = 0.07W KN
In cui W tiene conto dei carichi permanenti indotti da peso proprio,
portati e la quota quasi permanente dei carichi variabili, secondo
l’espressione di normativa:
Poiché per il carico variabile di esercizio ψ2=0, mentre per il carico
da neve ψ2=0.20, si può determinare complessivamente un “peso
sismico”:
W ≈5261 KN Fh = 368.27 KN
Questa azione è applicata nel baricentro della copertura (baricentro
delle masse), che nel nostro caso coincide con buona
approssimazione col baricentro delle rigidezze.
Dovremo
però
considerare
comunque
una
eccentricità
convenzionale, pari al ±2% della dimensione in pianta ortogonale
alla direzione del sisma considerata.
Per esempio rispetto alla direzione longitudinale si ha:
15
Ovviamente si intende che il torcente di piano può avere sia senso
orario che antiorario.
Per quanto attiene all’AZIONE DEL VENTO avevamo determinato:
pressione del vento sopravento: Qsop =0.80 (0.48) KN/m2
depressione del vento sottovento: Qsop =0.16 (0.48) KN/m2
inoltre si considera, come suggerito dalla circolare, per vento
spirante in direzione N-S (e S-N), un’azione orizzontale distribuita
sulla proiezione orizzontale della copertura pari a 0.08 KN/m2.
In direzione N-S complessivamente si ha, tenuto conto che il
prospetto dell’edificio ha dimensioni circa 9x72 m, che consideriamo
che metà della risultante della pressione si scarichi direttamente a
terra e che la dimensione in pianta è circa 72x96 m:
Fh,N-S = 9·72/2·(0.80+0.16)+72·96·0.08= 864 KN
In direzione E-O si ha:
Fh,E-O = 8.14·96/2·(0.80+0.16) = 375.09 KN
Questi carichi dovranno essere amplificati per le verifiche allo SLU.
16
Possiamo pertanto supporre che tutte queste azioni, sia quella
sismica, sia quella del vento, agiscano a livello della copertura.
Sulla determinazione delle sollecitazioni sui controventi solo queste
azioni orizzontali hanno effetto, pertanto per il solo loro
dimensionamento non è necessario considerare le altre azioni.
Con riferimento alle azioni in direzione N-S (sisma e azione del
vento non vengono combinate perché in presenza di sisma per il
vento si ha ψ2 =0), il sistema resistente rappresentato dai
controventi di falda è indicato in figura:
17
Che potrà essere calcolato come un sistema collaborante di 4 travi
reticolari del tipo mostrato di seguito, cui verrà delegata una quota
del carico orizzontale complessivo.
Il compito dei controventi di falda trasversali in questo caso è di
trasmettere ai controventi perimetrali longitudinali tale azione
orizzontale. Con la quale potrà essere dimensionato il sistema
controventante longitudinale.
Il dimensionamento dei controventi potrà avvenire risolvendo una
semplice struttura reticolare, tenendo conto, a seconda della
direzione della sollecitazione delle sole aste tese.
Discorso analogo può essere fatto per le azioni orizzontali in
direzione E-O.
18
Nel caso volessimo prendere in considerazione anche la rigidezza
alla traslazione orizzontale dei telai non controventati iperstatici
(abbiamo ipotizzato che il vincolo alla base potesse essere di
incastro), lo schema per i controventi di falda diverrebbe:
Perché parte dell’azione orizzontale si scaricherebbe sui telai
longitudinali non controventati, in ragione della loro rigidezza
rispetto ai telai perimetrali controventati. Si rende necessario allora
stabilire la rigidezza delle molle sopra riportate facendo un’analisi
sulla rigidezza allo spostamento laterale dei telai stessi, interni e
perimetrali.
Le reazioni così determinate in corrispondenza degli appoggi
cedevoli servirebbero a fare poi le analisi dei vari telai longitudinali
di controvento e non.
Ovviamente in questo caso anche quest’ultima analisi diverrebbe
più complessa per l’iperstaticità del problema.
Discorsi analoghi si potrebbero fare nel caso in cui si inserissero
anche telai di controvento interni.
Come detto il dimensionamento dei controventi dipende dalle sole
azioni orizzontali e non è influenzato dalle altre azioni. Così non può
dirsi per gli altri elementi del sistema controventante (i correnti e i
montanti del sistema reticolare).
Richiede attenzione il caso del collegamento di base delle colonna in
corrispondenza dell’aggancio del controvento, infatti in questo caso
se si minimizzano i carichi verticali e si massimizza l’azione
orizzontale si può verificare che il collegamento vada in trazione.
Questo è un caso particolare da tenere in conto per il progetto dei
tirafondi.
19
CORSO DI COSTRUZIONI
IN ACCIAIO
270 Laurea Magistrale
I anno – I semestre
ESERCITAZIONE:
CALCOLO DELLA STRUTTURA DI UN CAPANNONE
INDUSTRIALE SITO NELLA CITTÀ DI CAGLIARI
Parte 7
TITOLARE: Prof. Ing. Barbara De Nicolo
RELATORE: Ing. Daniel Meloni
VERIFICA PILASTRI
Procederemo infine alla verifica dei pilastri del capannone. Ci
limiteremo alla verifica di quelli che sostengono le travate principali,
tralasciando quelli perimetrali.
Dall’analisi delle travi principali e quindi dalle reazioni di appoggio
determiniamo l’azione di compressione esercitata sui pilastri.
Riepilogando:
Rp = reazione trave c. permanente (compreso p.p.) = 141.60 KN
Rvar = reazione trave c. variabile = 83.85 KN
Rp = reazione trave c. da neve = 72.15 KN
Consideriamo per ora solo i carichi verticali (a meno del peso
proprio del pilastro):
NED = 2·(1.3·Rp +1.5·Rvar +1.5·0.5·Rn )= 728 KN
Il profilo prescelto è un HEA260, con le seguenti caratteristiche:
H = 250 mm
B = 260 mm
sa = 7.5 mm
sf = 12.5 mm
A = 8682 mm2
Wy = 836395 mm3
Wz = 282120 mm3
Jz = 36675579 mm4
Jy = 104549360 mm4
ρ = 0.68 KN/m
Il profilo ha Classe 1.
Il peso proprio è pari a Pp = 7.50·0.68 =5.10 KN
da cui infine NEd = 733.10 KN
1
Facciamo la verifica a compressione:
σx,ED=
NED 733 x 103
=
=84.44 N/mm2 < 235/1.05
A
8682
verifichiamo l’instabilità flessionale, considerando la seconda
direzione con minore inerzia; in tal caso Jmin = 36675579 mm4:
lunghezza dell’asta H = 7.50 m (dallo spiccato di fondazione alla
piastra d’imposta della trave reticolare).
Se consideriamo i telai a nodi fissi, perché efficacemente
controventati, possiamo ipotizzare che β =1.0, pertanto lunghezza
libera di inflessione L0 = L = 7.50 m
determiniamo il carico critico elastico:
Ncr =
π 2 ⋅ E ⋅ Jmin
= 1351368 N = 1351.4 KN
2
L0
La snellezza è pari a λ = 115.4 < 200
Determiniamo la snellezza relativa:
λ=
A ⋅ fyk
Ncr
= = 1.23
α =0.34, da cui: Φ = 1.43 χ = 0.46
Quindi dobbiamo effettuare la verifica:
NbRD =
χ ⋅ A ⋅ fyk
γ M1
=
0.46 ⋅ 8682 ⋅ 235
= 899000 N= 899 KN > NED
1.05
2
Si fa osservare che alcune delle colonne che fanno parte dei telai
controventati sono sottoposte ad un’azione assiale aggiuntiva (la
componente verticale del tiro nei controventi). Però si tratta nel
nostro caso di colonne perimetrali pertanto si può verificare che
l’azione di progetto è comunque inferiore a quella appena
determinata.
Si potrebbe altresì considerare i difetti locali dell’asta, quali errore
di verticalità, difetto di rettilineità, eccentricità nei collegamenti ecc.
La norma, nella Circolare, consente di prendere in conto tali
problematiche in modo forfetario applicando un carico trasversale
uniformemente
distribuito
lungo
l’altezza
della
colonna
corrispondente ad un difetto di curvatura.
Tale carico è pari a: qh =
8 ⋅ NEd ⋅ e o,d
L2
In cui:
L = lunghezza (altezza) elemento;
NEd = azione assiale di calcolo;
e0,d = scostamento convenzionale di rettilineità dedotto dalla tabella
C.4.2.I fornita dalla Circolare e di seguito riportata.
3
Nel nostro caso:
L = 7.50 m; NEd=728 KN; e0,d =1/250.
Pertanto qh =0.42 KN/m
Con esso si può determinare un momento flettente, massimo in
mezzeria, pari a Md = 2.93 KNm, con cui si può fare una verifica di
pressoflessione ed eventualmente di instabilità.
Nel caso in cui si considerasse i telai non controventati collaboranti
alla rigidezza orizzontale dell’edificio, in virtù dell’incastro alla base
delle colonne, bisognerebbe valutare le azioni flessionali e taglianti
aggiuntive alla base delle stesse. In tal caso la colonna sarebbe a
tutti gli effetti pressoinflessa e quindi bisognerebbe effettuare le
relative verifiche di resistenza e instabilità.
4