Economia Applicata
Lezione 12
la concorrenza di prezzo
Prof. Giorgia Giovannetti
[email protected]
Giorgia Giovannetti
1
w1
w2
w3
w4
w5
w6
w7
w8
w9
w10
w11
w12
w13
w14
w15
martedi
giovedi
martedi
giovedi
martedi
giovedi
martedi
giovedi
martedi
giovedi
martedi
giovedi
martedi
giovedi
martedi
giovedi
martedi
giovedi
martedi
giovedi
martedi
giovedi
martedi
giovedi
martedi
giovedi
martedi
giovedi
martedi
giovedi
28
2
7
9
14
16
21
23
28
30
4
6
11
13
18
20
25
27
2
4
9
11
16
18
23
25
30
1
6
8
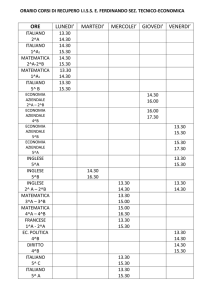
Intro
Intro, elasticitá
Il concetto di mercato, esempi
richiami micro, curve dei costi
Domanda, equilibrio di mercato, statica comparata, curve dei costi
Curve dei costi, forme mercato: concorrenza, monopolio
ESERCIZI concorrenza, monopolio, curve dei costi, ricavi
forme di mercato: concorrenza imperfetta e economia del benessere
esercizi su forme di mercato
forme di mercato concorrenza imperfetta e oligopolio
Oligopolio, curva di domanda ad angolo, benessere
Benessere Introduzione teoria dei giochi,
Primo compito
Vacanza pasqua
Vacanza pasqua
Soluzioni compito
vacanza
giochi Bertrand, Cournot, Stackelberg
giochi ripetuti, nozioni
Investimenti
Investimenti pubblici e privati
investimenti e incertezza
investimenti analisi costi benefici
esercizi su investimenti
Q&A
Lezione su crisi
esempi acqua e terra
secondo compito
Outline di oggi
• Soluzioni compito
• Riassunto lezione precedente
• Introduzione Teoria dei giochi: modello di
Bertrand
Primi cenni alla teoria dei giochi
• Le imprese oligopolistiche adottano un comportamento strategico: agiscono
in base alle mosse compiute dagli avversari per “rubare” quote di mercato.
• Per questo, spesso, in mancanza di accordi per cooperare, producono esiti
negativi per tutte (riduzione dei margini di profitto).
• La “teoria dei giochi” ha studiato il comportamento strategico tipico di
queste imprese.
• Esempio di “gioco non cooperativo” è il dilemma del prigioniero.
• Supponiamo che Bonnie e Clyde siano arrestati.
• Al momento dell’arresto hanno addosso armi illegali per il cui porto la
condanna è 1 anno.
• Vengono interrogati in stanze diverse contemporaneamente.
• Il magistrato propone a ciascuno un patto: se confessa e denuncia il
complice, gli verrà condonato il reato di porto d’armi e verrà liberato. Al
complice verranno dati 20 anni. Se entrambi confessano, la condanna è 8
anni (parziale condono per avere confessato).
Questa è la “matrice delle vincite (payoffs):
La strategia consistente nel confessare è detta strategia dominante. A entrambi conviene non conoscendo la scelta
dell’altro. Se potessero comunicare potrebbero cooperare e scegliere la strategia dell’omertà.
Per questo spesso le imprese oligopolistiche stabiliscono accordi espliciti o segreti (detti “di cartello” o “trust”), per
cooperare e mantenere così alti i profitti.
Esempi:
1. OPEC
2. Società assicuratrici
Gli stati moderni hanno adottato politiche “anti-trust” per proibire questi accordi.
Il dilemma del prigioniero
I numeri rappresentano anni di carcere
Giocatore 1
Il dilemma del prigioniero
Giocatore 2
C
N
-100
-10
C
-10
0
0
-2
N
-100
-2
0
I numeri rappresentano anni di carcere
Giocatore 1
Perché questo gioco è paragonato da Cabral
al”Dilemma del prigioniero”?
T
B
Giocatore 2
L
R
5
6
5
3
3
4
6
4
0
Dilemma del prigioniero e fissazione dei prezzi
(profitti)
impresa A
prezzo alto prezzo basso
prezzo alto
500 ; 500
100 ; 700
prezzo basso
700 ; 100
300 ; 300
impresa
B
fonte: A. Schotter Microeconomia, Giappichelli, Torino
La teoria dei giochi
Sarebbe stato possibile colludere per ottenere il
payoff (500,500).
Ma per entrambe le imprese ci sarebbe stato
l’incentivo a tradire l’accordo per ottenere un
payoff superiore
Fissazione dei prezzi, qual è la differenza rispetto
alla diapositiva precedente? (i numeri sono profitti)
impresa A
prezzo alto prezzo basso
prezzo alto
900 ; 900
0
; 500
500 ; 0
750 ; 750
impresa
B
prezzo basso
fonte: A. Schotter Microeconomia, Giappichelli, Torino
La teoria dei giochi
Studia con approccio formale l’interazione
strategica tra due o più soggetti
Introduzione
In molti mercati le imprese competono sui prezzi
–
–
–
–
Accesso ad Internet
Ristoranti
Consulenti
Servizi finanziari
In monopolio è indifferente scegliere prima il prezzo o la
quantità
In oligopolio invece è fondamentale in quanto
– la concorrenza dei prezzi è molto più aggressiva rispetto alla
concorrenza delle quantità
14
Concorrenza dei prezzi: Bertrand
In Cournot, il prezzo è stabilito da qualche meccanismo di
allocazione di mercato
Un approccio alternativo è ipotizzare che le imprese competano
sui prezzi: questo è l’approccio di Bertrand, che conduce a
risultati completamente diversi
Prendete un semplice esempio
–
–
–
–
–
due imprese che producono lo stesso bene (acqua???... frizzante)
le imprese decidono il prezzo a cui vendere il bene
ciascuna impresa ha un costo marginale pari a c
la domanda inversa è P = A – B.Q
la domanda diretta è Q = a – b.P (con a = A/B e b= 1/B)
15
La competizione “a la Bertrand”
Abbiamo bisogno della domanda “derivata” di ogni impresa
– domanda condizionata al prezzo praticato dall’altra impresa
Prendete l’impresa 2. L’impresa 1 pratica il prezzo p1
– se l’impresa 2 pratica un prezzo > p1 non vende nulla
– se l’impresa 2 pratica un prezzo < p1 ottiene tutto il mercato
– se l’impresa 2 pone un prezzo pari a p1 i consumatori sono
indifferenti tra le imprese:
il mercato si divide, presumibilmente, in quote uguali 50:50
– q2 = 0
se p2 > p1
– q2 = (a – bp2)/2
se p2 = p1
– q2 = a – bp2
se p2 < p1
16
La competizione “a la Bertrand” (2)
Possiamo illustrare tale funzione di domanda:
– la domanda è discontinua
– la discontinuità nella domanda comporta una discontinuità nei
profitti
p2
C’è un salto
in p2 = p1
p1
(a - bp2)/2
a - bp2
a q2
17
La competizione “a la Bertrand” (3)
I profitti dell’impresa 2 sono:
p2(p1,, p2) = 0
p2(p1,, p2) = (p2 - c)(a - bp2)
p2(p1,, p2) = (p2 - c)(a - bp2)/2
Chiaramente dipendono da p1.
se p2 > p1
se p2 < p1
se p2 = p1
Per qualche
arcano motivo!
Supponete che l’impresa 1 pratichi un prezzo “molto alto”: superiore
al prezzo di monopolio: pM = (a +bc)/2b
18
Che prezzo
La competizione “a la dovrebbe
Bertrand” (4)
praticare
L’impresa 2 otterrà un l’impresa 2?
Con p1 > (a + profitto
c)/2b,positivo
i profitti dell’impresa 2 sono:
A p2
Profittosolo
impresa
2
tagliando
i prezzi
a = p1
Prezzo di
l’impresa
2
ottiene
(a + c)/2b
monopolio
L’impresa
2
dovrebbe
metà
dei
profitti
o a livelli ancora più bassi
tagliare un po’ il prezzo p1 di monopolio
p2 < p 1
e ottenere quasi
tutti
E se l’impresa 1
i profitti di monopolio
praticasse
il prezzo(a + c)/2b?
p2 = p1
p2 > p 1
c
(a+bc)/2b
p1 Prezzo impresa 2
19
La competizione “a la Bertrand” 5
Supponete ora che p1 < (a + c)/2b
Finché
p1 > c,
prezzo
I profitti dell’impresa 2 sono: Che
Ovviamente, l’impresa 1
l’impresa 2 dovrebbe
deve praticare
Profitto impresa
farebbe2altrettanto
tagliare i prezzi dell’
ora l’impresa
e così ancora
impresa 1 2?
Allora
anche l’impresa
l’impresa
2 p2 < p1 2
dovrebbe avere prezzo c.
Con prezzo inferiore a c si ottiene
l’intero
mercato ma si fanno perdite
E se l’impresa
ogni
1 avesse per
prezzo
c?acquirente
p 2 = p1
p 2 > p1
c
p1(a+bc)/2b
Prezzo impresa 2
20
La competizione “a la Bertrand” (6)
Abbiamo ora la funzione di reazione dell’impresa 2 per ogni
prezzo praticato dall’impresa 1:
– p2* = (a + c)/2b
– p2 * = p1 - ε
– p2 * = c
se p1 > (a + c)/2b
se c < p1 < (a + c)/2b
se p1 < c
Simmetricamente, per l’impresa 1
– p1 * = (a + c)/2b
– p1 * = p2 - ε
– p1 * = c
se p2 > (a + c)/2b
se c < p2 < (a + c)/2b
se p2 < c
21
La competizione “a la Bertrand” (7)
Le
Funzione di
impresasi1 rappresentanoFunzione
funzioni reazione
di reazione
così di
reazione impresa 2
p2
R1
R2
(a + c)/2b
In equilibrio di
Equilibrio con
Bertrand
entrambe le imprese
entrambe
le imprese
che praticano
prezzo
pari a c
praticano
prezzi pari
ai costi marginali
c
p1
c
(a + c)/2b
22
Il modello di Bertrand rivisitato
Il modello di Bertrand chiarisce che la competizione sui prezzi
è molto diversa da quella sulle quantità
Dato che molte imprese stabiliscono i prezzi (e non le quantità),
ciò è una critica all’approccio di Cournot
Ma nella versione originale di bertrand viene criticato il fatto
che qualsiasi deviazione del prezzo anche infinitesimale
porta a un’immediata e completa perdita di domanda per
l’impresa che applica il prezzo più elevato
Possiamo considerare due estensioni del modello di Bertrand
– l’impatto dei vincoli di capacità
– la differenziazione di prodotto
23
I vincoli di capacità
Affinché in equilibrio si abbia p = c, entrambe le imprese devono avere
capacità sufficiente da coprire l’intera domanda al prezzo p = c
Ma quando p = c ottengono solo metà del mercato, e ci sarà quindi un
enorme eccesso di capacità
I vincoli di capacità possono dunque influenzare l’equilibrio
Considerate un esempio
– domanda giornaliera servizi sciistici sul monte Norda: Q = 6000 – 60P
– Q è il numero di sciatori giornalieri e P il prezzo dello skipass
giornaliero
– 2 stazioni: Punta Resia con capacità giornaliera 1000 e Sport Resort con
capacità giornaliera 1400 (le capacità sono fisse)
– il costo marginale dei servizi sciistici è €10 in entrambe le stazioni
24
Esempio
Il prezzo P = c = €10 è un equilibrio?
– la domanda totale a P=10 è 5400 (ben oltre la capacità)
Supponete entrambe le stazioni pongano P = €10: entrambe
hanno dunque domanda di 2700
Considerate Punta Resia:
–
–
–
–
aumentando i prezzi si perde parte della domanda
ma dove possono andare? Non certo a Sport Resort
alcuni sciatori non andranno a Sport Resort con i maggiori prezzi
ma allora Punta Resia sta facendo profitti sugli sciatori rimanenti
tramite un prezzo superiore a C’
– perciò P = €10 non può essere un equilibrio
25
Esempio (2)
Supponete che ad ogni prezzo tale per cui la domanda ad una
stazione è superiore alla capacità ci sia razionamento efficiente
– vengono serviti i turisti con la più alta disponibilità a pagare
Allora possiamo ricavare la domanda residuale
Assumete P = €60
– domanda totale = 2400 = capacità totale
– perciò Punta Resia ottiene 1000 clienti
– la domanda residuale per Sport Resort è
Q = 5000 – 60P ossia P = 83,33 – Q/60
– i ricavi marginali sono dunque R’ = 83,33 – Q/30
26
Esempio (3)
Domanda residuale e R’:
Supponete Sport Resort ponga P = €60
Vuole cambiare?
– dato che R’ > C’ Sport Resort
non vuole alzare i prezzi e
perdere clienti
– dato che QS = 1400 Sport Resort
impiega tutta la capacità e
non vuole ridurre i prezzi
Prezzo
€83,33
Domanda
€60
R’
€36,66
€10
La stessa logica vale per Punta Resia,
perciò P = €60 è equilibrio di Nash per questo gioco
C’
1.400
Quantità
27
Ancora i vincoli di capacità
La logica è piuttosto generale:
le imprese difficilmente sceglieranno di installare tanta capacità
da servire l’intero mercato quando P = C’
In equilibrio ottengono infatti solo una parte della domanda
– perciò la capacità di ciascuna impresa è inferiore a ciò che è
richiesto per servire l’intero mercato
– ma non c’è incentivo ad abbassare i prezzi fino ai costi marginali
Perciò la proprietà di efficienza dell’equilibrio di Bertrand perde
validità se ci sono vincoli di capacità
28
Differenziazione di prodotto
L’analisi originale assume inoltre che i prodotti offerti dalle
imprese siano omogenei
Le imprese hanno un incentivo a differenziare i prodotti
– per fidelizzare i clienti
– per non perdere tutta la domanda quando i prezzi sono superiori
a quelli dei rivali (mantenimento dei consumatori “più fedeli”)
29
Un esempio di differenziazione
Coca-Cola e Pepsi sono simili, ma non identiche.
Di conseguenza, con prezzo più basso non si ottiene l’intero
mercato.
Stime econometriche dicono che:
QC = 63,42 – 3,98PC + 2,25PP
C’C = €4,96
QP = 49,52 – 5,48PP + 1,40PC
C’P = €3,96
Ci sono almeno due metodi per ottenere PC e PP
30
Bertrand e differenziazione del prodotto
Metodo 1: calcolo differenziale
Profitto Coca-Cola: pC = (PC – 4,96)(63,42 – 3,98PC + 2,25PP)
Profitto Pepsi: pP = (PP – 3,96)(49,52 – 5,48PP + 1,40PC)
Derivate rispetto a PC per la Coca e a PP per la Pepsi
Metodo 2: R’ = C’
Riorganizzate le funzioni di domanda
PC = (15,93 + 0,57PP) – 0,25QC
PP = (9,04 + 0,26PC) – 0,18QP
Calcolate i ricavi marginali, uguagliate ai costi marginali,
risolvete per QC e QP e sostituite nelle funzioni di domanda
31
Bertrand e differenziazione del prodotto (2)
Entrambi i metodi restituiscono le funzioni di reazione:
PP
PC = 10,44 + 0,2826PP
PP = 6,49 + 0,1277PC
Possono essere risolte
per i prezzi di equilibrio
L’equilibrio di
Bertrand è alla
loro intersezione
RC
RP
€8.11
B
€6.49
I prezzi di equilibrio sono
entrambi superiori ai costi marginali
€10.44
PC
€12.72
32
Bertrand in un contesto spaziale
Un approccio alternativo: il modello di Hotelling
–
–
–
–
una Via Centrale sulla quale si distribuiscono i consumatori
rifornita da due negozi posti ai due estremi
ora i due negozi sono concorrenti
ciascun consumatore acquista esattamente una unità di bene
finché il prezzo pieno è inferiore a V
– un consumatore compra dal negozio che offre il minor prezzo
pieno
– i consumatori sopportano costi di trasporto pari a t volte la
distanza percorsa per raggiungere un negozio
Ricordatevi l’interpretazione più ampia del modello:
che prezzi praticheranno i negozi?
33
Bertrand in un contesto spaziale (2)
Prezzo
Assumete
che il1negozio 1
E se il negozio
ponga
prezzo
p1 e il negozio 2
alzasse
il prezzo?
pratichi un prezzo p2
p’1
p1
x’m
xm
Prezzo
xm segna la posizione del
p2
consumatore marginale,
quello che è indifferente
ad acquistare presso
l’uno o l’altro negozio
Tutti i consumatori a
E tutti
i consumatori alla
x
si
sposta
verso
sinistra:
m
m
Negozio 1sinistra di x comprano
Negozio 2
sua destra comprano
alcuni consumatori
dal negozio 1
passano al negoziodal
2 negozio 2
34
Bertrand in un contesto spaziale (3)
p1 + txm = p2 + t(1 – xm)
2txm = p2 - p1 + t
xm(p1, p2) = (p2 - p1 + t)/2t
Ci sono in tutto N consumatori
La domanda per l’impresa 1 è
Questa è la frazione
Come è
di consumatori chem
determinato x ?
comprano dall’impresa1
D1 = N(p2 - p1 + t)/2t
Prezzo
Prezzo
p2
p1
xm
Negozio 1
Negozio 2
35
Equilibrio di Bertrand
Profitti impresa 1:
p1 = (p1 - c)D1 = N(p1 - c)(p2 - p1 + t)/2t
p1 = N(p2p1 - p12 + tp1 + cp1 - cp2 -ct)/2t
Derivate rispetto a p1
N
(p2 - 2p1 + t + c) = 0
p1/ p1 =
2t
p*1 = (p2 + t + c)/2
Risolvete per p1
Questa è la
funzione di reazione
dell’impresa 1
E l’impresa 2?
Per simmetria, ha una funzione di reazione simile
p*2 = (p1 + t + c)/2
Questa è la
funzione di reazione
dell’impresa 2
36
Equilibrio di Bertrand (2)
p2
p*1 = (p2 + t + c)/2
R1
p*2 = (p1 + t + c)/2
2p*2 = p1 + t + c
R2
= p2/2 + 3(t + c)/2
p*2 = t + c
p*1 = t + c
Il profitto unitario di
ciascuna impresa è t
c+t
(c + t)/2
(c + t)/2 c + t
p1
I profitti aggregati per ogni impresa sono Nt/2
37
Equilibrio di Bertrand (3)
Due osservazioni finali
1) t è una misura dei costi di trasporto
– è anche una misura implicita del valore che i consumatori
ricavano dall’ottenere la loro varietà preferita
– quando t è grande la competizione si attenua
e i profitti aumentano
– quanto t è piccolo la competizione è più accesa
e i profitti diminuiscono
2) Le posizioni sono state assunte come esogenamente date:
supponete le imprese decidano la varietà del prodotto
– bilanciano la tentazione a “rubare clienti” avvicinandosi al rivale
– contro il desiderio di “ridurre la competizione” allontanandosi
38
Complementi strategici e sostituti strategici
Le funzioni di reazione sono molto diverse in Cournot e Bertrand
q2
– hanno inclinazioni opposte
– riflettono forme del tutto
diverse di competizione
– le imprese reagiscono
diversamente agli
incrementi di costo
delle rivali
Impresa 1
Cournot
Impresa 2
q1
p2
Impresa 1
Bertrand
Impresa 2
p1
39
Complementi strategici e sostituti strategici (2)
Supponete che aumentino i costi dell’impresa 2
– la funzione di reazione di Cournot
dell’impresa 2 si sposta verso il basso
• ad ogni output dell’impresa 1
l’impresa 2 ora produce di meno
q2
risposta
aggressiva
Impresa 1
dell’impresa 1Cournot
– l’impresa 1 aumenta l’output
risposta
passiva
e l’impresa 2 lo riduce
dell’impresa 1
– la funzione di reazione di Bertrand
p2
dell’impresa 2 si sposta verso l’alto
• ad ogni prezzo dell’impresa 1
l’impresa 2 vuole aumentare il suo prezzo
– il prezzo dell’impresa 1 aumenta
come quello dell’impresa 2
Impresa 2
q1
Impresa 1
Impresa 2
Bertrand
p1
40
Complementi strategici e sostituti strategici (3)
Se le funzioni di reazione sono inclinate positivamente
(es. Bertrand): complementi strategici
–
azioni passive inducono reazioni passive
Se le funzioni di reazione sono inclinate negativamente
(es. Cournot): sostituti strategici
– azioni passive inducono reazioni attive
Difficile determinare quale sia la variabile di scelta strategica:
prezzo o quantità
– scelta dell’output prima della vendita -> forse quantità
– piani di produzione facilmente modificabili e intensa
competizione per accaparrarsi i clienti -> forse prezzo
41