Ricerca di un elemento in un
vettore ordinato
Lezione n°10
Algoritmi Avanzati
Prof.ssa Rossella Petreschi
Idea
Variabili:
N: numero dei processori
y: elemento da cercare
X = (x1, x2, …, xn), tale che x1 x2 … xn: vettore in cui cercare y
l ed r (inizializzati a 0 ed n rispettivamente): estremi del vettore su cui si lavora;
q0,…qN+1 (relative a ciascun processore + 2 aggiuntive): indice degli elementi da
analizzare;
c0,…cN+1 (inizializzate a 0, cN+1 inizializzata ad 1): identificatori del sottovettore su cui
iterare.
Input: X, y
Output: i t.c. xi y xi+1
Passo 1: dividi iterativamente il vettore in sottovettori più o meno bilanciati finché il
numero di elementi nel sottovettore identificato non è N e controlla se X[qi]=y;
Passo 2: controlla se nel sottovettore di dimensione N è presente l’elemento cercato.
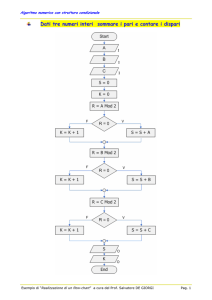
Algoritmo
P1:
c0 = 0; cN+1 = 1; l=0; r=n+1;
while (r-l) > N do
Pj:
for j = 1 to N pardo
if j = 1 then q0 = l; qN+1 = r
qj = l + j (r-l) / (N+1)
if y = X[ qj ] then return qj
else if y > X[ qj ] then cj = 0 else cj = 1
if cj < cj+1 then l = qj; r = qj+1
if j = 1 and c0 < c1 then r = q1
Pj:
for j = 1 to N pardo
if y = X[ l+j ] then return l+j
else if y > X[ l+j ] then cj = 0 else cj = 1
if cj < cj+1 then return l+j
if j = 1 and c0 < c1 then return l
Passo 1
Passo 2
Esempio
l
0
r
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
n = 14
N=2
y = 37
x - -22 -3 4 10 12 15 27 32 35 42 55 56 61 70
q0
q1
q2
0
c
l
4
1
6
7
8
9
10
11
x 10 12 15 27 32 35 42 55
q0 q1
0
c
q2
1
2
q3
3
0 0 1 1
r
5
2
q3
Passo 2
l
7
8
9
10
11
x 27 32 35 42 55
0
3
0 0 0 1
r
c
1
2
3
0 0 1 1
return 9
Complessità dell’algoritmo
•Ciascuna iterazione del Passo 1 richiede tempo O(1).
•Dimensione del sottovettore alla iterazione i-esima:
si+1 = si / (N+1) = s0 / (N+1)i = n+2 / (N+1)i
•Numero totale di iterazioni:
logN+1(n+2) = log2(n+2) / log2(N+1)
•Il Passo 2 richiede tempo costante.
Tempo complessivo richiesto dall’algoritmo: O(log2(n+2) / log2(N+1)).
Il modello di PRAM è CREW perché tutti gli N processori accedono
contemporaneamente alle variabili y, l, r e c.
Quando N = O(1), il costo complessivo dell’algoritmo è O(log n): pari all’ottimo nel
sequenziale.
Quando N = O(n) il tempo diventa costante.
Algoritmo pari/dispari
L’idea base è quella di far lavorare prima tutti i processori di indice pari e poi quelli di
indice dispari per evitare letture e scritture concorrenti nei confronti.
0
• for s = 1 to n/2 do
• for i = 0 to i < n-1 step 2 pardo
•Pi:
if x[i] > x[i+1] then swap(x[i], x[i+1])
• for i = 1 to i < n-1 step 2 pardo
•Pi:
if x[i] > x[i+1] then swap(x[i], x[i+1])
1
2
3
4
5
6
s=1 pari
8 5 9 2 4 3 6
s=1 dispari
5 8 2 9 3 4 6
s=2 pari
5 2 8 3 9 4 6
s=2 dispari
2 5 3 8 4 9 6
s=3 pari
2 3 5 4 8 6 9
s=3 dispari
2 3 4 5 6 8 9
Fine
2 3 4 5 6 8 9
•Richiede tempo O(n) su una PRAM EREW con O(n) processori.
•Il costo complessivo è O(n2).
Algoritmo pari/dispari
con p < n processori
Ogni processore Pi gestisce un blocco Si composto di b = n/p elementi.
Pi: ordina Si in modo sequenziale
for s = 0 to p/2 do
for i = 0 to i < p-1 step 2 pardo
Pi:
Si' = Merge(Si, Si+1)
Si = Si' [0, b-1]
Si+1 = Si' [b, 2b-1]
for i = 1 to i < p-1 step 2 pardo
Pi:
Si' = Merge(Si, Si+1)
Si = Si' [0, b-1]
Si+1 = Si' [b, 2b-1]
Il tempo richiesto è Tp = O(n/p log (n/p)) + p/2 O(n/p).
Se p = O(log n), il tempo Tp diventa O(n), ovvero costo totale O(n log n).
Ordinamento su PRAM CRCW
Sfruttiamo la scrittura concorrente per ottenere un semplice algoritmo di ordinamento.
Assumiamo una PRAM CRCW con scrittura concorrente della somma dei valori scritti.
xiniz
for i = 0 to n-1 pardo
for j = 0 to n-1 pardo
Pi,j:
if (x[ i ] > x[ j ]) or
(x[ i ] = x[ j ] and i > j) then c[ i ] = 1
for i = 0 to n-1 pardo
Pi,1: x[ c[ i ] ] = x[ i ]
7
5
3
8
5
0
1
2
3
4
1
2
3
4
0
1
2
3
4
xfin
3
5
5
7
8
Risultati dei confronti
effettuati
i
Con n2 processori il tempo richiesto è O(1).
Il costo totale è quindi O(n2).
0
C
3
1
0
4
2
0
1
2
3
4
j
0
1
2
3
4
F
F
F
V
F
V
F
F
V
V
V
V
F
V
V
F
F
F
F
F
V
F
F
V
F