Le prime osservazioni

Le prime osservazioni e i
primi modelli
Di Pietro Pantano
Centro Interdipartimentale della
Comunicazione
Università della Calabria
Indice
Osservazione dei
fenomeni terrestri
Osservazione dei
fenomeni astronomici
La Scienza greca
I modelli astronomici
La fisica aristotelica
Il sistema tolemaico
I fenomeni terrestri
Per l’uomo primitivo, i fenomeni naturali
sono causati da divinità, alcune volte
benevole o irate con gli abitanti della
Terra.
Tutto quel che accade è riconducibile non
a cause naturali, ma ad azioni divine.
Bisogna aspettare la Scienza greca perché
facciano la loro comparsa le prime teorie
interpretative.
Osservazioni astronomiche
Seq 1 - cd 4
A) Fin dall’antichità i fenomeni astronomici colpirono
l’immaginario dell’uomo, che imparò ad osservarli ed a
classificarli.
I più evidenti fenomeni celesti riguardano:
B) il moto apparente della volta celeste
C) le fasi lunari
D) la posizione del sole nel cielo ed i cicli stagionali
E) l’apparizione di comete e meteore
Video sulle osservazioni
astronomiche
QuickTime™ and a
Video decompressor
are needed to see this picture.
Disomogeneità ed anisotropia
del cielo stellato
Seq 2 - cd 4
Se osserviamo il cielo sopra di noi ci accorgiamo che:
A) Cambia a seconda dell’ora di osservazione con un
moto apparente da Est verso Ovest;
B) Cambia a seconda della direzione di osservazione;
C) Cambia a seconda della latitudine e della longitudine
D) Cambia a seconda delle stagioni
E) In determinati periodi alcuni astri sembrano apparire e
scomparire nel cielo
Video sul cielo stellato
QuickTime™ and a
Video decompressor
are needed to see this picture.
Le stelle fisse e i pianeti
Seq 3 - cd 4
A) Se osserviamo attentamente la volta celeste nella stessa
posizione ma in tempi differenti, ci accorgiamo che:
B) alcuni astri si ripresentano esattamente nella stessa
posizione gli uni rispetto agli altri e li chiameremo pertanto
Stelle Fisse
C) Altri invece cambiano a seconda dei giorni, delle stagioni e
degli anni, cioé hanno un movimento apparente rispetto alle
stelle fisse : i pianeti
D) Altri ancora appaiono solo in determinati periodi e poi
scompaiono: le comete
Video sulle stelle fisse e i
pianeti
QuickTime™ and a
Video decompressor
are needed to see this picture.
I cicli celesti: diurno,
mensile, stagionale
Seq 4 - cd 4
A) Nella sfera celeste due grandi astri sono dominanti: il Sole e la Luna
B) Il Sole, come tutti gli altri astri sorge ad Est e tramonta ad Ovest, scandendo la
durata del giorno.
C) la sua traiettoria nel cielo cambia nel corso di un anno, ritmando le stagioni.
Quando il sole é presente nel cielo, nessun altro astro, tranne la Luna in alcune
condizioni, é visibile
D) Il secondo grande astro é la Luna; visibile di notte, anch’essa sorge ad Est e
tramonta ad Ovest. La sua forma cambia nel corso del mese per le fasi lunari ,
passando da Luna Piena a Luna Nuova e di nuovo a Luna Piena.
E) I due astri cambiano la loro posizione relativa nel corso del giorni e dei mesi
rispetto alle stelle fisse.
Video sui cicli celesti
QuickTime™ and a
Video decompressor
are needed to see this picture.
I pianeti
Seq 5 - cd 4
A) Se escludiamo il Sole e la Luna, solo cinque astri la cui
posizione varia rispetto alle stelle fisse sono osservabili ad
occhio nudo: Mercurio, Venere, Marte, Giove e Saturno
variano
B) Non tutti sono osservabili nella medesima direzione ed allo
stesso tempo, ma bisogna girare lo sguardo ed anche attendere
la loro comparsa nel cielo;
C) Questi erano gli unici pianeti noti fin dall’antichità; bisogna
aspettare Galileo e la scoperta del cannocchiale per osservarne
di nuovi
Video sui pianeti
QuickTime™ and a
Video decompressor
are needed to see this picture.
Comete e meteore
Seq 6 - cd 4
A) Alcuni astri compaiono nel cielo in determinati periodi; si comportano come
pianeti nel senso che varia la loro posizione rispetto alle stelle fisse, ma poi non
riappaiono più: questi astri si chiamano comete.
B) Molti di questi corpi celesti furono osservati fin dall’antichità e la loro
apparizione fu registrata dagli astronomi del passato: la più famosa é la cometa di
Halley;
C) l’ultima cometa che é apparsa ed é stata visibile ad occhio nudo é la cometa di
Hale-Bopp
D) Bisognò aspettare il 1759 perché fosse confermato che alcune comete potessero
ripresentarsi dopo un periodo di tempo più o meno lungo com’é il caso della cometa
di Halley, che ha una periodicità di 76 anni circa
Video su comete e meteore
QuickTime™ and a
Video decompressor
are needed to see this picture.
La volta celeste
Seq 7 - cd 4
A) In realtà, se osserviamo attentamente il cielo verso Nord nell’emisfero
boreale, ci accorgiamo che una stella non si muove, non cambia cioé la sua
posizione nel corso della notte: é la stella polare.
B) Le altre stelle sembra che girino attorno a questa stella, descrivendo delle
circonferenze. Una parte della circonferenza finisce dietro l’orizzonte e non
é più visibile. Per questo le stelle sembra che si spostino da Est verso Ovest.
Quelle che invece restano sempre sopra l’orizzonte sono dette circumpolari.
C) La Terra pertanto sembra sia contenuta in una sfera, detta Sfera Celeste,
sulla quale sembra siano fissati tutti gli astri;
D) Questa sfera sembra ruotare attorno ad un asse passante per i poli
terrestri. I punti in cui l’asse di rotazione incontra la sfera celeste sono detti
“poli celesti”.
Video sulla volta celeste
QuickTime™ and a
Video decompressor
are needed to see this picture.
Ancora un video sulla volta
celeste
La Grecia
La Scienza greca
La scienza moderna deve molto all’eredità
degli antichi greci.
Questi hanno iniziato a considerare i
fenomeni come naturali, piuttosto che
dovuti a cause soprannaturali.
Essi introdussero ragionamenti formali e li
applicarono alla matematica ed alla
geometria.
Aspetti generali della
Scienza greca
Lo studio e la conoscenza della natura fu
definita filosofia naturale
La rappresentazione del mondo era
consistente con la filosofia
Fu data preferenza alla comprensione
delle aspirazioni degli oggetti piuttosto
che ai principi
La scienza fu separata dalla religione
Non esiste nessuna causa soprannaturale
Basi della scienza greca
Le teorie fisiche sono basate su
considerazioni metafisiche a priori
La logica è la chiave per la comprensione
Esistono relazioni significative tra numeri
e geometria
Il primo periodo
Talete (VII sec. A. C.)
rimuove Dio dai fenomeni naturali
Pitagora
Immagine di Pitagora
Il teorema di Pitagora
da un testo arabo
Pitagora (VI sec. A. C.)
visione mistica
i numeri e la geometria forniscono un
modello concettuale di Universo
Numerologia e misticismo
Simmetria, bellezza, verità, perfezione e
semplicità sono tutti concetti correlati
Il cerchio è la più perfetta forma geometrica
La Grecia
Immagini di Platone
L’età aurea
Platone (IV sec. A.C.)
La geometria entra nella Scienza
Perfezione sferica-->orbite circolari
primo modello consistente con le
osservazioni
bassa opinione della filosofia naturale
(influenzato da Socrate)
Le idee sono eterne, reali; le cose vanno e
vengono
L’età aurea/2
Platone (continua)
Obiettivo del filosofo: determina la verità
dietro le apparenze
• APPARENZA: il moto del sole e dei pianeti, e le fasi della
luna sono disordinati
• VERITA’: Le traiettorie dei pianeti sono circonferenze
perfette
– il cerchio è la forma più perfetta
– i pianeti sono perfetti
– i numeri e la geometria sono perfetti
– la realtà è geometria e numeri
I solidi platonici
 I poliedri regolari (tetraedro, cubo, ottaedro e icoesaedro) corrispondono ai
quattro elementi fondamentali ( acqua, aria, terra, fuoco), mentre il
dodecaedro corrisponde all’universo
Platone conosceva le
proprietà elettriche dei pesci
Primi modelli: universo a due
sfere
Seq.11 - cd4
A) Già a partire dal IV secolo avanti Cristo, i Geci utilizzarono per rappresentare
l’universo il modello a due sfere: la Terra, che costituisce la prima sfera, é al centro
di un’altra sfera rotante dove sono collocate le stelle.
B) Il Sole, la Luna e gli altri cinque pianeti noti a quel tempo si pensava che si
muovessero in uno spazio tra le due sfere.
C) Il grande problema dell’astronomia antica é stato lo studio del moto irregolare dei
pianeti e la determinazione della loro posizione sulla volta celeste (ricordiamo che la
parola pianeta deriva da una parola greca che significa errante, e che il Sole era
considerato uno di tali pianeti).
D) Mentre si era in grado di completare tavole molto rigorose sulla posizione dei
vari pianeti nel corso del tempo, il modello a due sfere non era assolutamente in
grado di spiegare e predire tali moti.
Video sui primi modelli
QuickTime™ and a
Video decompressor
are needed to see this picture.
Epicicli e deferenti
A) Vari tentativi furono fatti per rappresentare il moto dei pianeti. Uno di questi
fu la teoria degli Epicicli e dei Deferenti elaborata tra il terzo e il secondo secolo
avanti Cristo.
B) Questa teoria é basata sulla rotazione con velocità costante di un punto che si
muove su un piccolo cerchio, l’epiciclo, attorno ad un secondo punto che si
muove sulla circonferenza di un secondo cerchio, il deferente. Il Pianeta P é
posto sull’epiciclo ed il centro del deferente coincide col centro della Terra.
C) Questo sistema tenta di rappresentare il moto irregolare del pianeta rispetto
alle stelle ed il moto giornaliero del pianeta rispetto alla Terra.
D) Purtroppo le osservazioni sperimentali differivano da quelle previste
teoricamente con questo modello.
Video su Epicicli e deferenti
QuickTime™ and a
Video decompressor
are needed to see this picture.
Questione Platonica
Quali moti circolari uniformi e ordinati bisogna
considerare per ciascun pianeta per ottenere la
sua apparente traccia irregolare nel corso del
tempo?
Questo è uno degli obiettivi degli astronomi
La definizione di realtà è cambiata profondamente
nel corso della storia
Eudosso (IV sec. A.C.)
 Studente di Platone
 Sfere dentro sfere
(visione omocentrica)
 combinazione di moti
circolari multipli
 27 sfere sembravano
sufficienti per i 7 corpi
pesanti
 La causa del moto è
ignorata
 Sono predette le
posizioni dei pianeti
Immagine di Aristotele
Aristotele ( 384-322 A. C.)
 Studente di Platone
 E’ stato un osservatore oltre che un pensatore
è reattivo rispetto agli sforzi di Socrate e Platone di riformulare
le leggi senza tener conto dei fatti empirici
 Raffinò il modello di Eudosso
considerò il moto delle sfere simile a meccanismi
introdusse il primum movens
aumentò fino a 56 il numero di sfere interagenti per cancellare
le irregolarità
Pose le basi per l’avvento del sistema tolemaico
 E’ il fondatore di un paradigma scientifico e filosofico
durato molti secoli
La scuola di Atene
Il sistema aristotelico del
mondo
Le sostanze
possiedono proprietà
che ne determinano il
comportamento
L’universo è fatto da 5
sostanze con una
collocazione preferita
Il sistema aristotelico del
mondo / 2
 Combina le sfere
omocentriche con la
filosofia platonica
 Il Primum Movens è
l’orologiaio del mondo
il modello d’universo è
meccanicistico
simile ad un meccanismo di
sfere interconnesse
Non esistono relazioni
causali tra tutti i corpi
pesanti
Il sistema aristotelico del
mondo : Teorie del moto
Il moto di qualsiasi tipo richiede una motivazione
Il moto naturale è causato dal desiderio di ciascun
elemento di trovare la sua collocazione naturale in
relazione alla sua leggerezza o pesantezza
i moti celesti sono causati dal primum movens
Debolezze della teoria
scarsa precisione osservativa
le dimensioni della luna variano di circa il 10%
la brillantezza dei pianeti varia molto durante il moto
L’Egitto
Alessandria e l’impero
ellenistico
Alessandria è uno dei centri intellettuali
del mondo greco
L’atmosfera della città è più pratica e
meno metafisica di Atene
Famosa per la sua biblioteca che
conteneva almeno 400.000 volumi
Hanno studiato in questa città Archimede
ed Euclide
Il faro di Alessandria
Aristarco ( III sec. A. C.)
Considera la terra rotante e l’eliocentrismo
Le sue idee sono deboli per tre ragioni
principali:
Il sistema è qualitativo: non fa nessun calcolo dei
cammini planetari
è contrario al paradigma dominante
• non spiega i moti sublunari
• E’ empio in quanto pone la Terra in moto nell’universo
Non considera i parallasse
Parallasse
Parallasse stellare
Parallasse angolare
Eratostene ( 235 - 195 A. C.)
Usò la Geometria per
misurare la
circonferenza della
Terra
Calcolò la curvatura
dai differenti angoli di
illuminazione
Osservazioni di Eratostene
 I greci avevano intuito la
rotondità della Terra
 Osservando la forma delle
ombre nelle eclissi
 Notando che alla distanza le
vele della nave apparivano
prima della nave stessa
 Per misurare il raggio,
Eratostene partì
dall’osservazione che a Siene,
a differenza di Alessandria, il
Sole di mezzogiorno illuminava
il fondo dei pozzi
Considerazioni di Eratostene
 Analogamente le
colonne a Syene non
proiettavano ombra.
 Allora, misurando
l‘ombra proiettata ad
Alessandria, poteva
dedurre l’angolo tra le
due città, rispetto al
centro della Terra
Calcoli di Eratostene
Conoscendo la
distanza tra le
due città, poté
quindi risalire al
raggio della
Terra;
Bisogna aspettare
il XVII con Picard
per avere una
stima migliore
Euclide ( 330 - 275 A. C.)
Sistematizzò la geometria
Gli elementi di Euclide è considerato il Libro più
influente dopo la Bibbia
Usò la logica per la risoluzione di problemi
Effettuò la costruzione di molte figure
geometriche
Introdusse il linguaggio matematico moderno:
assiomi, teoremi, dimostrazioni, corollari
Immagine di Euclide
Ipparco ( II A. C. )
Fece accurate osservazioni mogliorando gli
strumenti di misura
calcolò la distanza del Sole e della Luna dalle eclissi solari
Il calcolo della distanza solare non era corretta
Introdusse i cataloghi stellari
Introdusse latitudine e longitudine
rigettò l’eliocentrismo di Aristarco
aggiunse epicicli ed eccentricità
Molte modifiche raggiunsero il culmine con
Tolomeo
Calcolo della posizione
stellare
Seq. 8 - cd 4
A) Per determinare la posizione di un astro nel cielo, si ricorre alla misura di due angoli:
altezza e Azimut.
B) L’altezza misura la distanza angolare dell’astro sopra l’orizzonte.
C) L’Azimut misura la distanza angolare dell’oggetto sull’orizzone, partendo da Nord in
direzione Est.
D) Questo metodo, creato nei tempi più antichi, consente di individuare immediatamente
la posizione di un astro nel Cielo, assegnandogli due coordinate sferiche, l’azimut e
l’altezza. Non consente però di creare atlanti stellari universali in quanto la posizione
dell’astro dipende dal luogo e dal tempo dell’osservazione.
E) L’astronomia moderna individua invece gli astri direttamente sulla volta celeste, sulla
quale sono state proiettate le coordinate terrestri: latitudine e longitudine. Questo
permette la determinazione della posizione dell’astro indipendentemente dall’osservatore
e consente la creazione di cataloghi stellari universali.
Video sul calcolo della
posizione stellare
QuickTime™ and a
Video decompressor
are needed to see this picture.
Tolomeo ( 100-170 d.C. )
La sua vita è poco nota
Scrisse testi di Ottica e di Geografia
L’almagesto fu una compilazione ed una
collezione di dati
Il titolo greco era Grande Sintesi o grande compilazione,
tradotto in arabo come Al Majisti
E’ un compendio dell’astronomia greca
Presenta nuovi lavori originali sul moto planetario
presenta cataloghi stellari
Fornisce metodi di calcolo
E’ la base dell’astronomia fino la XVII secolo
Immagine di Tolomeo
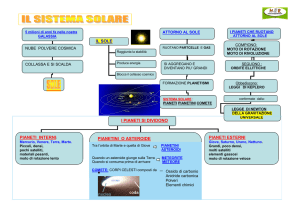
Il sistema tolemaico
Seq.13 - cd 4
A) Il sistema degli epicicli e deferenti fu soltanto il punto di partenza di ulteriori
sviluppi che condussero all’elaborato sistema di Tolomeo.
B) Tolomeo indrodusse una serie particolare di sfere per spiegare non solo i moti del
Sole e della Luna, ma anche le regolarità e le irregolarità che venivano osservate nel
moto apparente dei sette pianeti noti fino ad allora: Luna, Sole, Mercurio, Venere,
Marte, Giove e Saturno.
C) Nel sistema geocentrico di Tolomeo, la Terra era immobile al centro
dell’universo; intorno ad essa orbitavano i pianeti descrivendo delle traiettorie assai
complesse.
D) Per rendere ragione dell’apparente irregolarità del loro moto Tolomeo spiegava
che ogni pianeta descriveva un cerchio, detto epiciclo, il cui centro descriveva a sua
volta una grande orbita intorno alla Terra.
E) Quasi sempre le rappresentazioni del modello tolemaico rappresentavano solo i
deferenti dei pianeti.
Video sul sistema tolemaico
QuickTime™ and a
Video decompressor
are needed to see this picture.
Il sistema tolemaico /2
 Mantenne l’astronomia dividendola dalla cosmologia
 usò la matematica senza indagare sulle cause
 mantenne l’eleganza matematica della trattazione antica
 Fece accurati calcoli per costruire tavole planetarie da
usare nella navigazione
Il limite era legato all’accuratezza della misura dei tempi
Usò 80 epicicli
Spiegò il moto retrogrado
Spiegò la differente velocità
 Spiegò i cambiamenti nella brillantezza e le dimensioni
Eccentricità ed equanti
Eccentricità
Equanti
Sistema tolemaico / 3
 Fornisce argomenti a favore della sfericità della Terra
perfezione della sfera
 Il modello tolemaico era il più semplice in accordo con i
dati sperimentali
 Gli astronomi successivi cercarono di rendere il sistema
tolemaico ragionevole e coerente con i dati fisici
le sfere devono essere trasparenti
Lo spazio tra le sfere deve essere riempito da una sostanza (
l’etere)
Definirono le proprietà di tale sostanza