G-Lez_7-tras-verific..

Transitori di Corrente nei Trasformatori
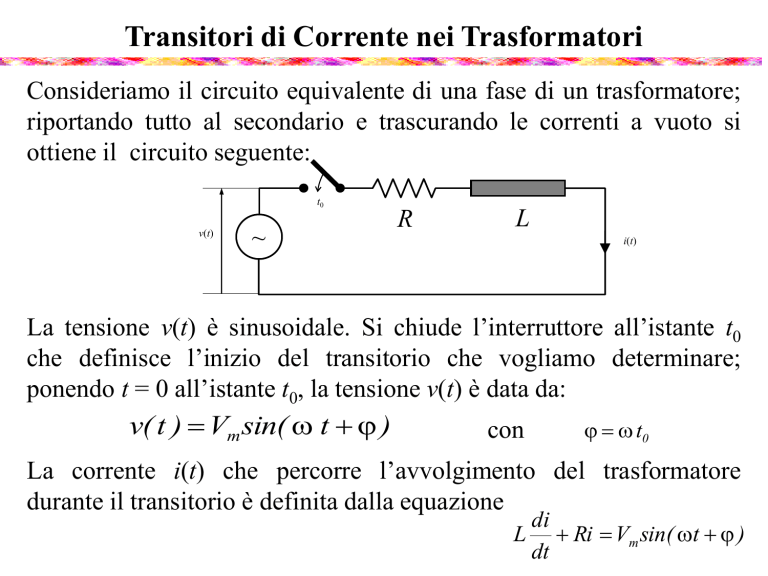
Consideriamo il circuito equivalente di una fase di un trasformatore;
riportando tutto al secondario e trascurando le correnti a vuoto si
ottiene il circuito seguente:
t0
v(t)
~
R
L
i(t)
La tensione v(t) è sinusoidale. Si chiude l’interruttore all’istante t0
che definisce l’inizio del transitorio che vogliamo determinare;
ponendo t = 0 all’istante t0, la tensione v(t) è data da:
v( t )  Vm sin(  t   )
con
   t0
La corrente i(t) che percorre l’avvolgimento del trasformatore
durante il transitorio è definita dalla equazione
L
di
 Ri  Vm sin( t   )
dt
L’omogenea associata a questa equazione differenziale è data da
di
L
 Ri  0
dt
ed ha come soluzione
R
t 

i0 ( t )  C e
con
L
L’integrale generale è quindi dato da i(t)=i0(t)+ip dove ip è un
integrale particolare la cui forma è del tipo
i p  A cos(  t   )  Bsin (  t   )
di p
L
 Ri p  Vm sin( t   )
dove A e B sono delle costanti. Ora
dt
e la derivata di ip vale
di p
  A sin(  t   )  B cos(  t   )
dt
sostituendo:
L  (  A sin(  t   )  B cos(  t   ))  R( A cos(  t   )  Bsin (  t   ))  Vm sin(  t   )
( BR  AL )sin(  t   )  ( BL  RA ) cos(  t   )  Vm sin(  t   )
eguagliando i coefficienti dei termini simili si ottengono le due
equazioni che permettono di determinare i due coeff. incogniti.
BL 
A
BL   RA  0
R
2 2

BL

L

BR 
L  Vm ;
BR  B
 Vm ;
BR  AL  Vm
R
B( R 2  2 L2 )  RVm
BL 
L RVm
A

R
R R 2  2 L2
R
RV
B  2 m2 2
R  L
A
 LVm
R 2  2 L2
L’integrale particolare che soddisfa l’equazione diff. risulta quindi
 L Vm
RVm
ip   2
cos(  t   )  2
sin(  t   )
2 2
2 2
R  L
R  L
L
R


i p  Vm  2 2 2 cos(  t   )  2 2 2 sin(  t   )
R  L
 R  L

i p  Vm  p cos(  t   )  q sin(  t   )
Semplificando
dove è stato posto
p
sapendo che
 L
R 2  2 L2
q
r
p cos   qsin   r sin(    )
2 L2  R 2
1
p q  2

( R  2 L2 )2 R 2  2 L2
2
R
R 2  2 L2
r
2
 L
L
  arc tan
 arc tan
R
R
p2  q2
  arc tan
p q 
2
1
2
   arc tan
p
q
R 2  2 L2
L
R
L’integrale particolare cercato assume quindi la forma
ip 
Vm
R  L
2
2
2
sin (  t     )
Gli elementi R ed X=L sono i componenti dell’impedenza di corto circuito:
Z cc  R  j L
ed in modulo:
R 2  2 L2  Z cc
Vm
ip 
sin (  t     )
Z cc
In definitiva possiamo scrivere
L’integrale generale dell’equazione, dato da i( t )  i0 ( t )  i p risulta
i( t )  C e

R
t
L
Vm

sin (  t     )
Z cc
La costante C si determina dalle condizioni iniziali. Per t=0 => i(0)=0. Si ha
V
C  m sin(    )  0
Z cc
C
Vm
sin(    )
Z cc
La soluzione generale dell’equazione generale è quindi
 Vm
  RL t Vm
i( t )  
sin(    ) e 
sin (  t     )
Z cc
 Z cc

2V
icc (t ) 
Z cc
R
 t

L
sin ( t     )  sin (   ) e 


;
L
tan  
R
L’andamento della icc nel tempo (a partire dall’istante t = 0 in cui si chiude
l’interruttore M) è indicato nel grafico seguente, in cui si è posto:
Ip : valore massimo della corrente di corto circuito
Iccr : valore di cresta della corrente di corto circuito a regime;
i
R
icc(t)
corrente unidirezionale
 t
2V
sin (   ) e L
Z cc
Ip
Iccr
t
La corrente di corto circuito a regime si determina per t=>
Vm
iccr ( t ) 
sin (  t     )
Z cc
L
  arc tan
R
La corrente di corto a regime è sfasata in
ritardo rispetto alla tensione dell’angolo
ed ha (com’è ovvio) un valore efficace I cc 
ed un valore di cresta
V
Z cc
I ccr 
2V
Z cc
Se la resistenza degli avvolgimenti Rcc è trascurabile nei confronti della reattanza
Xcc=L (Rcc<<Xcc), si ha che /2 e quindi la corrente di corto a regime, sfasata di
90° in ritardo rispetto alla tensione, è data da:
2V
icc ( t ) 
cos (  t   )
Z cc
Il valore di picco della corrente di corto circuito, Ip, dipende dall’angolo di fase della
tensione applicata, =t0 e quindi dall’istante t0 in cui ha inizio il corto circuito.
Nel grafico seguente è riportato l’andamento della corrente di corto per diversi valori
dell’angolo  –  (arctan(-L/R) dipende dagli elementi circuitali e dalla pulsazione
 che possiamo ritenere costante dal momento che il sistema funzione a 50 Hz)
Ip / Iccr
icc(t)
   = 90°
2
   = 60°
   = 30°
1
Iccr
Ip
0
t
   = 0°
Nelle ordinate del grafico precedente è anche riportato il rapporto fra valore di picco Ip
della corrente e valore di cresta della corrente di corto a regime Iccr .
Il più alto valore di tale rapporto si ha per  –  =90°, cioè per  = /2, dove si ha
Ip/Iccr = 2.
In realtà la parte iniziale del transitorio è descritta da un circuito equivalente più
complesso di quello utilizzato, che tenga conto anche delle capacità degli
avvolgimenti ecc. ;
il transitorio che ne deriva è del tipo di quello indicato nel grafico seguente, in cui il
valore di picco della corrente di corto è inferiore a Ip=2Iccr.
Ip/Icc
t
Per i calcoli di progettazione di solito si assume Ip/Iccr = 1,8 , cioè
I p  1,8 I ccr  1,8  2 I cc  2,54558  I cc  2,55 I cc
e
I cc 
V
X cc
è il valore efficace della corrente di corto a regime. Per quanto riguarda la durata
delle sovracorrenti, si assume di solito che esse non superino il tempo tmax = 1 s, in
quanto si conta su un efficace e tempestivo intervento delle protezioni.
Le sovracorrenti producono sollecitazioni termiche e meccaniche.
• Le sollecitazioni termiche vengono integrate dalla massa
dell’avvolgimento e si possono trattare considerando il fenomeno
adiabatico.
• Le sollecitazioni meccaniche sono invece proporzionali al quadrato
del valore istantaneo della corrente.
• Le sollecitazioni elettrodinamiche negli avvolgimenti, in presenza
delle correnti nominali, sono modeste, con effetti termici e meccanici
trascurabili, anche le sovracorrenti di inserzione, pur essendo 15-20
I0 sono dell’ordine delle correnti di pieno carico.
•È invece necessario effettuare delle verifiche meccaniche in
corrispondenza delle correnti di corto circuito, tali correnti infatti, non
producono di solito effetti termici apprezzabili, ma possono creare
problemi meccanici anche assai rilevanti, soprattutto in presenza di
lacune o di dissimmetrie negli avvolgimenti.
FORZE ELETTRODINAMICHE
Per capire a quali sforzi elettrodinamici sono sottoposti gli avvolgimenti dei
trasformatori, partiamo dal fenomeno che si verifica quando un conduttore percorso
da corrente I è immerso in un campo magnetico B:
F  B  I l
Sul conduttore si sviluppa una forza elettrodinamica F che agisce in direzione
perpendicolare sia al campo magnetico B sia alla corrente I.
Il verso della forza F è determinato dalla regola della mano sinistra: è quello del
pollice della mano sinistra disposta lungo il conduttore nel verso della corrente I,
con le linee del campo B entranti nel palmo della mano.
Il modulo della forza F è dato da:
F  B  I l
dove l è la lunghezza della parte di conduttore interessata dal campo magnetico B.
 V s 
 Wb 
 V  A s 


Dimensionalmente:  N    T  A  m    2   A  m   
A
m

   

2
m
m 


m


Conduttore rettilineo percorso da corrente continua e immerso in un mezzo
omogeneo lineare di estensione infinita:
• la corrente che scorre nel conduttore crea attorno a sé un campo di induzione
magnetica, le cui linee sono di forma circolare, centrate rispetto al conduttore e
giacenti in piani ortogonali al conduttore stesso.
• il verso del campo di induzione magnetica è dato dalla regola della mano destra:
considerando il pollice nel verso in cui scorre la corrente, il verso del campo di
induzione magnetica è dato dal verso di chiusura della mano.
L’intensità del campo di induzione magnetica prodotta dalla corrente I è data da:
I
B
2 d
 = permeabilità magnetica del mezzo,
d = distanza dal conduttore
SFORZI ELETTRODINAMICI
In conseguenza a questi due fenomeni, si ha che, tra due conduttori percorsi da
corrente si instaurano delle forze, di attrazione o di repulsione a seconda dei versi
delle correnti, dovute al campo magnetico creato da un conduttore e agente
sull’altro.
1° CASO: il conduttore di lunghezza l percorso da corrente I2 è immerso in un
campo magnetico B1 prodotto dalla corrente I1:
 I1
B1 
2 d
Di conseguenza, il conduttore percorso da corrente I2 è sottoposto a una forza
elettrodinamica F nel verso determinato dalla regola della mano sinistra:
F  B1  I 2  l 
 I1 I 2l
2 d
SFORZI ELETTRODINAMICI
Analogamente, il conduttore di lunghezza l percorso da corrente I1 è immerso in un
campo magnetico B2 prodotto dalla corrente I2:
B2 
 I2
2 d
Di conseguenza, il conduttore percorso da corrente I1 è sottoposto a una forza
elettrodinamica F nel verso determinato dalla regola della mano sinistra:
F  B2  I1  l 
 I 2 I1l
2 d
Questa forza F è di attrazione se i
conduttori sono percorsi da correnti
concordi (entrambe uscenti o entrambe
entranti).
SFORZI ELETTRODINAMICI
2° CASO: se i conduttori sono percorsi da correnti discordi, si ha:
F
 I1 I 2l
2 d
Questa forza F è di repulsione se i conduttori
sono percorsi da correnti discordi (una
uscente e una entrante).
SFORZI ELETTRODINAMICI NEI
TRASFORMATORI
Cosa succede nei trasformatori?
i1
R1
L 1
i’2
i2
L2
R2
i0
v1
Lm1
e1
e2
Z
v2
In ciascuna fase del trasformatore, la corrente entra da un avvolgimento (primario)
e esce dall’altro avvolgimento (secondario): quindi le correnti che circolano negli
avvolgimenti BT e AT sono discordi tra loro.
AVVOLGIMENTO CONCENTRICO
Per esempio, nel caso di avvolgimento
concentrico, si hanno forze radiali di repulsione
tra i conduttori BT e AT:
Rb
 le forze sono di compressione
dell’avvolgimento BT sul nucleo e di
dilatazione radiale dell’avvolgimento AT verso
l’esterno.
Il valore massimo dell’induzione che si
raggiunge nel canale di separazione tra i due
avvolgimenti è:
Bmax 
0 N1 2 I1
h

0 N 2 2 I 2
h

0 N 2 I
h
dove I1, I2 e I sono i valori efficaci delle correnti.
Bmax
BT
AT
Fr
X
O
Fr
h
a1 b a2
AVVOLGIMENTO CONCENTRICO
In corrispondenza di ciascun avvolgimento
l’induzione magnetica cresce linearmente dal
valore nullo al valore massimo Bmax.
Se si considera il valore medio pari alla metà
del valore massimo e la lunghezza media della
spira pari a 2Rb, la forza elettrodinamica media
a cui è sottoposto ciascun avvolgimento è data
da:
B
F  max  N 2 I  2 Rb
2
F
0 N 2 I
2h
 N 2 I  2 Rb 
 N I Mcc
FM  6,4 * 
4
 10
0 Rb
h
2

 N 2I
 lm

(N)
 h

Rb
Bmax
BT
AT
Fr
X
O
Fr
h
2
a1 b a2
Osservazioni:
• La forza elettrodinamica dipende dal quadrato della corrente.
• La corrente è periodica alternata sinusoidale con frequenza f = 50 Hz.
• Di conseguenza, la forza elettrodinamica avrà una componente periodica
alternata sinusoidale con frequenza doppia di quella della corrente, cioè 100 Hz.
nucleo
Si considerino avvolgimenti cilindrici e coassiali di
cui quello esterno (ES) è generalmente di AT,
mentre quello interno (INT) è generalmente di BT.
Fra gli avvolgimenti ES e INT del trasformatore
sono sollecitati dalle

forze di repulsione radiali Fr

forze di compressine assiali Fa
E’ dunque necessario determinare le forze
meccaniche che sollecitano gli avvolgimenti al fine
di prevedere opportuni ancoraggi meccanici che
impediscano la deformazione o la distruzione
meccanica degli avvolgimenti stessi.
Fa
Fa
Fr
Fr
Aest
Aint
Fa
Fa
Sforzi Radiali:
forze radiali di
dilatazione FES
In pianta si ha:
forze radiali di
compressione FINT
INT
ES
a1
R
b
a2
Gli avvolgimenti esterno (ES) ed interno (INT) sono
separati da un canale di spessore b. Si consideri la
distanza elettromagnetica degli avvolgimenti c,
definita nel calcolo delle reattanze di dispersione:
a  a2
c b 1
3
h
a2/3
a1/3
Rb
c
c
Per determinare le forze che sollecitano l’avvolgimento si usa il principio dei
lavori virtuali. Sia W(xyz) l’energia del campo magnetico connesso con gli
avvolgimenti e F(xyz) la forza generata da questo campo magnetico.
Consideriamo una componente di tale forza lungo una determinata coordinata, ad
esempio la componente Fx(x ) lungo l’asse x;
Se la geometria del sistema varia lungo la coordinata x di una quantità
infinitesima dx, il lavoro svolta dalla relativa componente della forza F è dato da
dL=Fx(x)dx
Questo lavoro può svolgersi solo per effetto di una variazione dW dell’energia del
campo W, per cui si ha (conservazione dell’energia)
Fx(x)dx-dW=0
e quindi
Fx(x)=dW/dx
Poiché dobbiamo determinare le forze radiali e supponiamo che entrambi gli
avvolgimenti siano costruiti in modo da avere una simmetria cilindrica,
assumeremo come coordinata di riferimento la coordinata radiale r .
Avvolgimento Esterno:
Si assume come distanza di riferimento la distanza elettromagnetica c.
FINT
FES
FINT
h
a)
FES
b)
Rb
Rb
c
c
c
dc
c
Supponiamo ora che per effetto delle forze FES l’avvolgimento esterno si deformi
simmetricamente provocando un incremento dc della coordinata c. Possiamo
scrivere
FES (c)dc=dW
dove W è l’energia del campo relativa all’intero avvolgimento;
quest’ultima è data da
1
1 X cc
2
2
W( t ) 
2
L i( t ) 
2 
i( t )
dove Xcc è la reattanza di corto circuito dell’avvolgimento ed i(t) la corrente che lo
percorre. La reattanza di cto.cto. è data da
2 pc
X cc  2  f  0 N
h
dove N è il numero di spire di un avvolgimento (NAT o NBT) e p=2Rb è il perimetro
medio del canale. Poiché si ritiene che la deformazione dell’avvolgimento sia solo
radiale, l’altezza dell’avvolgimento h rimane costante, l’eq. diventa
X cc ( c )  A  c
con
A  2 f 0 N 2
p
h
costante, e si ha
dW 1 A 2
1 Ac
2
da
cui
risulta
FES 

I
W 
i( t )
dc 2 
2 
In prima approssimazione, A può essere determinato dalla reattanza nominale di
cto.cto. (valore determinato in assenza di deformazioni dovute al corto circuito),
ottenendo A=Xcc/c e quindi
1 X cc
FES 
i( t )2
2 c
ricordando che Ip=2.5 Icc=2.5 V/Xcc , il valore massimo della forza è
2
1 X cc 2 1 X cc 
V 
2 ,5 2 V 2
FES 
Ip 
2 ,5
 
2 c
2 c
X cc 
2 c  X cc
2
semplificando 2 ,5  3,125  
2
e X cc  Z cc
risulta
V2
V2
V2
FES  


2 f c X cc 2 f c X cc 2 f c Z cc
La forza
V2
FES 
2 f c Z cc
PES
è dovuta al campo magnetico creato dall’intero
avvolgimento, e quindi è la risultante delle forze di
dilatazione che, sulla base dell’ipotesi fatta di
avvolgimento omogeneo e a simmetria cilindrica, sono
uniformemente distribuite su tutto l’avvolgimento.
Questo significa che l’avvolgimento esterno è soggetto
ad una pressione, dall’interno verso l’esterno, data da
RES
PES 
dove
RES è il raggio medio dell’avvolgimento
(approssimazione).
Per valutare lo sforzo che sollecita l’avvolgimento,
consideriamo una generica sezione dell’avvolgimento.
Se indichiamo con dS=RES d h un elemento di
superficie del cilindro che costituisce l’avvolgimento,
valutato in corrispondenza del raggio medio, la forza
dF che agisce su dS è data da
dF  PES  dS
FES
F
 ES
( 2 RES )  h l ES h
h
FS
dES
Fx
RES
FS
E la sua componente lungo l’asse x è
dFx  PES cos   dS  PES RES h cos  d
La risultante, lungo l’asse x, delle forze che agiscono sul semicilindro che stiamo
considerando è quindi
2
Fx 
 PES RES h cos  d  PES RES h sin 2  2 PES RES h
2
 2
FS
FES
FES
Fx  2
RES h 
2 RES  h

dF
dS
dFx

V2
V2
sapendo che FES 
si ottiene Fx 
2 f c Z cc
2 f c Z cc
RES
Questa forza è bilanciata dalle due forze di trazione
F
Fs=Fx/2 che agiscono sull’avvolgimento nella
sezione considerata; questa sezione di avvolgimento è data da Savv=dES h
per cui è sollecitata da uno sforzo di trazione
2
S
F
Fx
FES
S  S 

d ES h 2 d ES h 2  d ES h
V
S 
4  f  Z cc  c d ES h
x
Fx
L’eq. esprime lo sforzo di trazione
che sollecita
l’avvolgimento, e tale sforzo deve essere inferiore allo
V2
sforzo massimo ammesso max per quel tipo di struttura:
S 
4  f  Z cc  c d ES h
s <max.
A titolo indicativo si può ritenere che per un avvolgimento
di trasformatore sia  max  8 kg/mm2
Lo sforzo s è un valore medio, di prima approssimazione, ottenuto ipotizzando un
avvolgimento cilindrico massiccio ed omogeneo, uniformemente sollecitato.
In realtà le singole spire che giacciono sullo stesso piano diametrale, anche se percorse
dalla stessa densità di corrente, sono sollecitate forze diverse che diminuiscono
all’aumentare della distanza dal nucleo per la non uniformità dei flussi concatenati (la
Fx diminuisce all’aumentare di c):
le spire più interne sono sollecitate da una forza maggiore, e quelle più esterna da una
F1  F3  F6
forza minore.
F1
interno
F3
avvolgimento
F6
esterno
Colonna
Studio ad elementi finiti per la visualizzazione
degli sforzi elettrodinamici
Flusso
disperso
Avv.BT
Avv.AT
Risultanti
di forze
Cassone
V2
V2
S 
K
4  f  Z cc  c d ES h
Z cc
K
1
4  f  c d ES h
dove K è un fattore che dipende dalla frequenza (50 Hz) e dai parametri geometrici di
dimensionamento degli avvolgimenti. Poiché Zcc=Vcc/In , facendo riferimento alla
2
2
tensione nominale (V = Vn) , si ha:
V
V
S  K
K
Vcc
Z cc
A parità di valori di K e della tensione
di corto circuito vcc% , lo sforzo
aumenta con la potenza nominale
della macchina;
In realtà anche la tensione di corto
circuito aumenta con la potenza
nominale, per cui l’incremento degli
sforzi meccanici con la potenza
nominale ha all’incirca l’andamento
mostrato nella figura seguente (valori
indicativi):
VI n
Pn
K
K
Vcc
Vcc%
In
V
Avvolgimento Interno
La forza radiale di compressione che sollecita
l’avvolgimento interno ha (ripetendo lo stesso
ragionamento fatto in precedenza) la stessa
espressione
della
precedente,
facendo
ovviamente riferimento ai parametri geometrici
dell’avvolgimento interno; si ha cioè
FINT
RINT
FES
FINT
h
Aest
Aint
V2

2 f c Z cc
PINT
RINT
Facendo ancora l’ipotesi che l’avvolgimento
interno sia un unico cilindro omogeneo dotato di
simmetria cilindrica, la forza FINT dà luogo ad
una pressione (di compressione) data da :
appoggi
PINT 
FINT
F
 INT
( 2  RINT )  h l INT h
Questa pressione è contrastata da n appoggi verticali,
ancorati al nucleo del trasformatore, posti alla distanza
b
lINT 2 RINT

n
n
Consideriamo un settore di questo avvolgimento, compreso fra due appoggi contigui
come schematizzato nel disegno seguente:
PINT
b
dINT
RINT
b
h
Questo tratto di avvolgimento può essere trattato come una trave, di lunghezza b,
spessore dINT e larghezza h, incastrata alle estremità, uniformemente caricata dalla
forza Fc  PINT  h b
P
INT
dINT
b
h
2
h d INT
W 
6
Il modulo di resistenza a flessione di questa trave è dato da
Sappiamo inoltre che
l’avvolgimento è dato da
l’andamento
del
momento
flettente
FINT b  x x 2 1 
M( x ) 
  2 
2 b b 6 
Il momento flettente massimo si ha nella mezzeria della trave e vale
M max
Fc b PINT h b 2


24
24
che
sollecita
Fc b PINT h b 2
M0 

12
12
Mentre quello sugli incastri (x=0; x=b) è dato da
e quest’ultima sollecitazione risulta quella massima (M0>Mmax).
Quindi il massimo sforzo a flessione che sollecita l’avvolgimento, che si ha agli
2
2
incastri, risulta
 b 
M
hb
6
1
I 
max
W
 PINT
12 h d
2
INT


PINT 
2
 d INT 
aumenta con la distanza fra gli appoggi b e diminuisce all’aumentare dello spessore
dINT dell’avvolgimento. La pressione che sollecita l’avvolgimento interno è data da
2
V
FINT
F
FINT 
PINT 
 INT
mentre FINT è
2 f c Z cc si ha, allora
( 2  RINT )  h l INT h
1 V2
1
b2
I 
2
2 2 f c Z cc 2 RINT h d int
con
K INT
1 1
b2

2
4 2 f c RINT h d INT
1 V2
b2
V2
I 
 K INT
2
4 2 f Z cc c RINT h d INT
Z cc
 I  K INT
VI n
P
V2
 K INT
 K INT n
Vcc I n
Vcc V
vcc%
A parità di KINT e della tensione di corto circuito percentuale, lo sforzo a flessione
aumenta con la potenza nominale della macchina.
Sforzi Assiali
Con riferimento a due avvolgimenti cilindrici,
concentrici, omogenei ed a simmetria cilindrica, le forze
generate dalle correnti che circolano negli avvolgimenti
sono di compressione per ambedue gli avvolgimenti.
Queste forze possono raggiungere valori elevati, e
quindi pericolosi per l’integrità meccanica degli
avvolgimenti, durante il transitorio di corto circuito.
Per valutare queste forze e gli sforzi di compressione
che ne derivano, si ricorrere ancora al principio dei
lavori virtuali.
Si consideri un solo avvolgimento (interno o esterno)
Fa
Fa
Aest
Aint
Fa
Fa
Si ipotizza la deformazione dovuta alle forzi assiali si manifesti
solamente con una variazione dh dell’altezza h
dell’avvolgimento; con riferimento alla figura si ha che
Fa
dh
FA( h )  dh  dW
dove W è l’energia del campo relativa all’intero avvolgimento
W( t ) 
h
1
1 X cc
L i( t )2 
i( t )2
2
2 
con Xcc reattanza di corto circuito dell’avvolgimento ed i(t) corrente che lo percorre.
La reattanza di cto.cto. Vale
pc
X cc  2  f  0 N 2
h
dove N è il numero di spire di un avvolgimento (NAT o NBT) e p è il perimetro medio
del canale (vedi par. 2.2.1); si ha quindi
e si ottiene
1
1
2 p c 2
2 p c 2
W
2 f 0 N
i  0 N
i
2
h
2
h
dW 1
1
 1  2
2
2 p c 2
FA 
 0 N p c  2  i   0 N
i
2
dh 2
4
h
 2h 
La forza FA risulta negativa rispetto al sistema di coordinate utilizzato, e quindi è di
compressione.
V
Il suo valore massimo si ha in corrispondenza del picco di corrente I p  2 ,5 I cc  2 ,5
X cc
Pertanto il valore della forza assiale di compressione che deve essere utilizzato per il
calcolo degli sforzi è
2
1
pc
FA  0 N 2 2
4
h
2

V 
p
c
V
2
2
,
5

1
,
6

N
0


2
2
X
h
X
cc 
cc

A questa forza corrisponde uno sforzo di compressione dell’avvolgimento
FA
pc
V2
2
A 
 1,6 0 N
2 Ravv d avv
( 2 Ravv d avv  h ) h X cc2
pc V2
 A  1,6 0 N
2
Volavv h X cc
 2Ravv d avv h
2
dove
Volavv
è il volume dell’avvolgimento.
ESEMPIO
In=150 A
lm=250 cm
Im=215 A
h=155 cm
N=500
Icc=3520 A
2
 500  215  250
F  6.4
 1140kg

4
 10
 155
2
 500  3520  1.8  250
F  6.4
 104000kg

4
10

 155
Questo esempio mostra come non sia possibile
dimensionare le strutture per resistere agli sforzi
meccanici di un corto secco a valle del trasformatore
Il rame elettrolitico è duttile e quindi le bobine e gli
avvolgimenti tendono ad adattarsi agli sforzi
Per il dimensionamento degli sforzi meccanici si
considera un aumento del 20%-30% rispetto alla 2In
che corrisponde al picco di corrente che si viene a
determinare nei transitori sotto carico
Il corto netto immediatamente a valle del trasformatore
non lo riesco a tenere, pena la realizzazione di
trasformatori immensi.
Se avviene, il trasformatore esplode.
AVVOLGIMENTO DOPPIO CONCENTRICO
Nell’avvolgimento
doppio
concentrico,
l’avvolgimento BT è diviso in due metà, una
disposta vicino al nucleo e l’altra all’esterno.
BT
In questo caso, il valore massimo
dell’induzione è pari alla metà rispetto al caso
concentrico semplice:
Bmax 
0 N1 2 I1
2h

0 N 2 2 I 2
2h

0 N 2 I
2h
Mentre la forza elettrodinamica risulta un
quarto rispetto al caso concentrico semplice:
F
0 Rb
4h

 N 2I

Bmax
Rb
X
Fr
O
Fr
Fr
AT
Fr
h
a1/2 a2 a1/2
b
2
X
b
Avvolgimento a Bobine Alternate
B max vale: BM=0H = 0NI/h*cs
Fm 
 0l m
2h  cs
NI 
2
2
(N)
AVVOLGIMENTI CONCENTRICI SPOSTATI
ASSIALMENTE O CON LACUNE
Si ricerca la simmetria degli avvolgimenti e si cambia il verso di
circolazione della corrente ad alcune bobine
Fa
h”
BT
h
AT
Fa
AVVOLGIMENTI CONCENTRICI SPOSTATI
ASSIALMENTE O CON LACUNE


Nel caso di avvolgimenti concentrici spostati
assialmente o con lacune di solito dovute alla
regolazione di tensione sono presenti sforzi assiali che
tendono a sfilare i due avvolgimenti.
Nel caso di avvolgimenti spostati assialmente si ha un
incremento di induttanza di dispersione circa pari a:
2
 h"
l"  N   R10 7 (H)
 h
2
1

R = raggio dell’avvolgimento in cm.

Poichè per uno spostamento dh” il lavoro delle forze
esterne deve essere pari alla corrispondente
variazione dell’energia magnetica si ha:
1 2
Fa dh"  I1 dl"
2

da cui
1 2 dl"
Fa  I1
2 dh"
Si ottiene quindi la forza assiale:
I12 N12
Fa  2 Rh" (N)
h

E’ necessario tenere conto che tutte le forze
considerate variano con una frequenza pari a 2f.
Forze Elettromagnetiche sul Nucleo




Le forze che agiscono sull’avvolgimento interno si
trasmettono al nucleo della colonna
Tali forze tendono ad avvicinare tra loro i lamierini ed
a ridurre i traferri equivalenti
Sono proporzionali ad I2 e quindi a B2
Sono pulsanti a 100 Hz
DIMENSIONAMENTO DEL CASSONE
Si assumono come parametri di progetto i seguenti
dati:
Sorgenti di calore:
 Pfe: perdite nel ferro
Pcu1, Pcu2: perdite negli avvolgimenti primario e
secondario (80 - 90% delle perdite totali)
Temperature di riferimento
 Temperatura esterna dell’aria a=40°C (convenzionale,
norme)
 Temperatura massima ammissibile, dettata dalla
classe di isolamento (es.:olio in classe A => 105 °C)
 Mf= temperatura massima nel ferro
Mcu= temperatura massima del rame
 Mo= temperatura massima dell’olio
 mo= temperatura media dell’olio
 min o= temperatura minima dell’olio

La temperatura dell’olio cresce lungo la verticale raggiungendo
il massimo vicino al coperchio
Temperatura funzionamento per la classe A = 105°C
Salto di temperatura che deve essere garantito dal sistema di
raffreddamento =65°C
Condizioni normali di funzionamento:
Mo< o =60°C
mo< o =50°C
Mo / mo= 1.1 - 1.15
Mo- min o=20- 30°C
Lamiere per cassoni
Psm [W/dm2] potenza smaltita per unità di superficie
dal materiale scelto per realizzare il cassone o
superficie necessaria per smaltire 1 W di potenza
persa (es.: 35-40 cm2/W, spessore 1-2 mm, pressione di
tenuta 10 kg/cm2)
Altezza del Cassone
Hc=H+2hg+bsup+binf
dove
Hc : l’altezza complessiva del cassone
H: altezza di colonna
hg: altezza dei gioghi
bsup e binf: battenti di olio della parte superiore ed inferiore del
trasformatore. Possiamo fissare bsup=15-30 cm e binf=5-10 cm i
due battenti
Il battente inferiore ampio è necessario per consentire alla
fanghiglia di olio di depositarsi sul fondo senza che ci siano
problemi per la circolazione
Il battente superiore deve essere abbastanza ampio per
consentire il moto convettivo dell’olio. Si può abbassare nel
caso di forzatura di circolazione
Dimensionamento delle Alette del Mantello
Se scegliamo una struttura ad alette, per modellare e realizzare
la necessaria superficie di scambio termico siano:
a:passo di alettatura,
h=altezza di aletta
a: passo interno
b=passo esterno
le alette devono essere dimensionate in modo che non si creino
ristagni o moti turbolenti nelle intercapedini
a
a
b
h
Si fissano delle dimensioni di
riferimento
45<a<75 mm
a=10-75 mm
h=60-300
b/a=2.5-3
h/a =4.5-5.5
Devo determinare la lunghezza del perimetro del cassone che
circonda e contiene il trasformatore stesso. Tra cassone e
trasformatore ho la tensione di fase
Perimetro
interno Pi
z
Re
Ri
y
h
Parete Cassone
X
Perimetro
esterno Pe
Siano Pi e Pe i perimetri interno ed esterno del cassone,
rispettivamente
Pi=4X+2(Ravv+y) Pe=4X+2(Ravv+y+h)
L’area della superficie totale radiante è:
A=HcPe
La superficie necessaria per smaltire il calore prodotto
all’interno del trasformatore è
St= Psm Pd
Se Hc è l’altezza del cassone, lo sviluppo in lunghezza del
perimetro, comprese le alettature è
L=St/Hc
Inoltre
L=N(a+b+2h)=N(a+2h)=Pi+N2h
N=(L-Pi)/2h
(N deve essere intero e pari per simmetria)
essendo
a=a+b=Pi/N
(b/a=2.5-3)
Fisso h e ricavo tutti i dati che mi servono per progettare le
alette
Va segnalato che il processo è iterativo in quanto si stima l’area
necessaria a smaltire la potenza persa, si calcola la lunghezza
del mantello, (l’altezza è fissata), si calcolano il numero e le
dimensioni delle alette e si correggono i dati ottenuti per
ottenere una struttura simmetrica. Si ricalcolano tutte le
dimensione alla luce dei dati che sono stati fissati per ottenere
dimensioni di facile realizzabilità e controllo
VERIFICA DELLE SOVRATEMPERATURE:
Metodo delle Resistenze Termiche
Si verifica se i salti termici sono quelli previsti
fe
Pfe
cu1
Pcu1
Pcu2
M o
Rcu1 o: RT avv.1 olio
cu2
Rcu2 o: RT avv.2 olio
Rcu2 o
Ro a : RT oliocassone-aria
Rcu1 o
Rfe o
m o
min o
a
Rfe o: RT nucleo olio
Ro a
 Rfe o Rcu1 o Rcu2 o: serie di resistenze di conduzione e
convezione (R=Rcond+Rconv)
Ro a : resistenza di conduzione in serie con il
parallelo delle resistenze di convezione e di
irraggiamento esterno

Def di Resistenze Termiche: RT nucleo olio
si trascura la conduzione
R feo
1

 0 A fe
Afe: superficie di contatto nucleo olio in m2 (con canali di raff.)
0: coeff. di convezione => 80 (W/m2°C)
RT rame olio (si trascura la conduzione)
R cu o
1

 0 A cu
Acu: superficie di contatto rame olio in m2
0: coeff. di convezione => 80 (W/m2°C)
Per Acu, che è la superficie dell’avvolgimento a contatto con
l’olio, si ricorre alla relazione
Acu=kNlm(2B+k’2H)
dove (k=0.8, k’=0,5
B
H
Per avvolgimenti a bobina stilizzati a forma di toroide si
utilizza sempre una relazione empirica
Acu=2kcN(a+b)+ 2k’N(a2-b2)
dove:
k è un coefficiente che tiene conto
del cattivo contatto tra rame ed olio
per la presenza dei distanziatori
bobina-bobina (k=0.8)
c
a
b
k’ tiene conto della superficie sottratta allo scambio termico per
la presenza dei separatori primario e secondario
c altezza di bobina
a e b raggi esterni ed interni di bobina
RT olio aria
R o a
R ca R ia
 R o c 
R ca  R ia
RT olio cassone
R o c
1

 ocuA c
0c: coeff. di convezione olio cassone => 35 (W/m2°C)
Ac: superficie totale esterna del cassone in m2
u: rapporto tra la superficie di contatto olio-cassone e
superficie esterna
RT cassone aria
R ca
1

 ca yA c
0c: coeff. di convezione cassone-aria => 6-8 (W/m2°C) con
velocità dell’aria di circa 1m/s
y: coefficiente correttivo della convezione (<1), di valore minore
di uno, dipendente dal tipo di radiatore o tubo considerato
R i a
1

 ia A i
ia: coeff. di irraggiamento.
Con colori grigi normali=> 6 (W/m2°C)
Ai: superficie esterna di irraggiamento (superficie di inviluppo)
Ai
Sia i=Ai/Ac rapporto tra superficie radiante e quella esterna
allora:
1  1
1 


R oa 

A c  35u 8y  6i 
u, y, i dipendono strettamente dalla forma del cassone

cassone liscio: u=1, y=1, i=1

cassone alettato: u1, y dal grafico, i=a/(2h+ a)

a
a
b
h

cassone a tubi: u1, y=0.6 - 1, i calcolato (y basso => elevato
numero di radiatori e/o tubi lunghi)


cassone a radiatori: u1, y fornito dai costruttori, i calcolato
VERIFICA DELLE SOVRATEMPERATURE
cu< o =65°C
Mo< o =60°C
mo< o =50°C
min o< o =40°C
cu o =15°C
Mo- min o =20°C
Si deve verificare che le sovra-temperature stiano nei limiti
previsti. Con riferimento alla rete termica:
Pcu
cu o  Pcu R cu o 
 o A cu
Pfe
feo  PfeR feo 
 o A fe

Pd  1
1


mo  Pd R oa 

Ac   ocu  ca y   i i 
cu  mo  cu o
fe  mo  feo
Si deve verificare che le
sovratemperature siano
nei limiti prescritti
SISTEMA ONAF
I ventilatori spingono l’aria contro i tubi o radiatori.
La velocità dell’aria è circa 2 m/s; ciò implica che:
caf: coeff. di convezione aria forzata => 13 - 16 (W/m2°C)
Si suppone un salto termico tra l’aria fredda e calda di 10 °C
La portata di aria Q [m3/s]
P
Q
v
1220   a
SISTEMA OFAN
Si applicano pompe di circolazione dell’olio. Si aumenta il coeff.
Di convezione dell’olio, specialmente quello tra olio e cassone
(tutti gli  sono funzione della velocità ed aumentano con essa)
SISTEMA OFAF
Il salto termico dell’olio è contenuto attorno a 8 -10 °C (metà
rispetto ad ONAN); l’aria subisce un incremento di 20 - 25 °
La portata dell’olio si stima in Qo=5 - 7 l/min per 1 kW di
perdita; la portata di aria Qa=2 - 2.5 m3/min per kW di perdita
 coeff. di convezione olio aria-aumentano con la velocità
La prevalenza aumenta con il numero di canali di
raffreddamento
SISTEMA OFWF
Il salto termico dell’olio è circa 8°C; l’acqua subisce un
incremento di 15 °C a partire da una T=25°C
La portata dell’olio si stima in Qo=5 - 7 l/min per 1 kW di
perdita; la portata di acqua Qaq=1 m3/min per kW di perdita
con una velocità di 0.7 l/min
VERIFICA DELLE SOVRATEMPERATURE
Utilizziamo un metodo empirico consigliato dalle norme
Siano Pp le perdite del trasformatore. Il valore del salto di
temperatura tra parti attive ed aria esterna può essere stimato
con la relazione:
 M 
0.25Pp
A  0.8S t  0.001Pp
dove A è la superficie radiale esterna (A=HcPe) e tiene conto del
contributo di calore irradiato ed St è la superficie totale del
cassone
Se il dimensionamento è stato correttamente eseguito
M<50°C (47°C-49°C)
Si fa una verifica sperimentale in sala prove posizionando le
termocoppie nella parte alta del trasformatore
Un’altra relazione empirica fornisce la sovra-temperatura
media dell’olio rispetto al cassone
 m 
0.13Pp
A  0.85S t
e deve risultare che M/ m=1.1-1.5
Si può valutare anche la sovra temperatura media dell’olio a
contatto con il cassone
M  m
 0 
2
Esistono anche formule empiriche che valutano le sovra
temperature per il rame ed il ferro di colonna sull’olio
circostante
SOVRATEMPERATURE DEL RAME/OLIO
Per avvolgimenti a bobina stilizzati a forma di toroide si
utilizza sempre una relazione empirica
Cu
PCu

3k t A Cu
dove 3 è il numero di colonne,
kt è il coefficiente di trasmissione del calore (80 [W/m2°C]
Acu è la superficie dell’avvolgimento a contatto con l’olio e
Cu è la sovratemperatura del rame sull’olio
Acu si stima con una relazione empirica
Per avvolgimenti a bobina stilizzati a forma di toroide si
utilizza sempre una relazione empirica
Acu=2kcN(a+b)+ 2k’N(a2-b2)
dove:
k è un coefficiente che tiene conto
del cattivo contatto tra rame ed olio
per la presenza dei distanziatori
bobina-bobina (k=0.8)
c
a
b
k’ tiene conto della superficie sottratta allo scambio termico per
la presenza dei separatori primario e secondario
c altezza di bobina
a e b raggi esterni ed interni di bobina
Per avvolgimenti a spirale, tipici delle BT, per stimare le
sovratemperature, si ricorre alla medesima relazione empirica
Cu
PCu

3k t A Cu
ed i parametri hanno lo stesso significato già indicato
Per Acu, che è la superficie dell’avvolgimento a contatto con
l’olio, si ricorre alla relazione
Acu=kNlm(2B+k’2H)
dove anche k e k’ hanno il significato
già spiegato in precedenza (k=0.8, k’=0,5)
Inoltre, il salto deve cadere nello stesso
intervallo di valori
B
H
SOVRATEMPERATURE DEL FERRO/OLIO
Facendo riferimento alla medesima relazione
 Fe
PFe

3k t A C / G
dove
AC=2Rchckf
AG=2(Sg+Pglg )
kf tiene conto della presenza dei gradini, Rc ed hc sono il raggio
e la altezza di colonna
mentre Sg è la sezione di base, Pg il perimetro e lg la lunghezza
dei gioghi
I salti di temperatura devono rimanere sotto i 10 °C