Flusso del campo elettrico e teorema di
Gauss
Flusso di un campo vettoriale uniforme
Problema (idrodinamico)
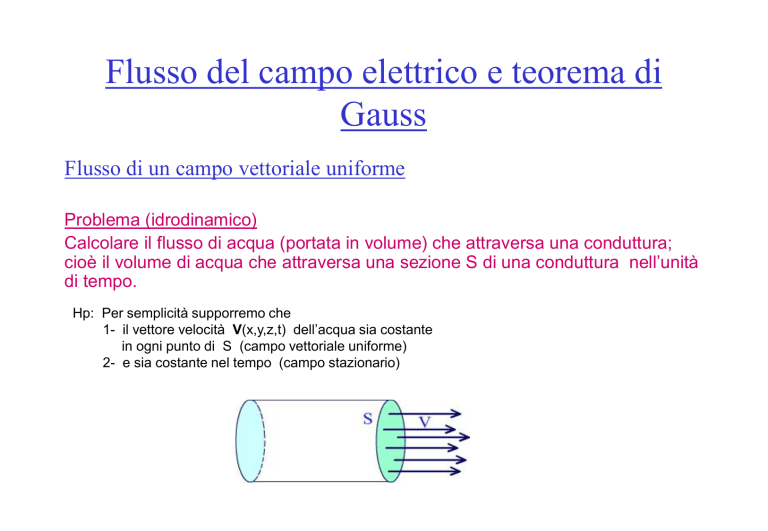
Calcolare il flusso di acqua (portata in volume) che attraversa una conduttura;
cioè il volume di acqua che attraversa una sezione S di una conduttura nell’unità
di tempo.
Hp: Per semplicità supporremo che
1- il vettore velocità V(x,y,z,t) dell’acqua sia costante
in ogni punto di S (campo vettoriale uniforme)
2- e sia costante nel tempo (campo stazionario)
Caso A
Il vettore velocità è perpendicolare alla sezione S della conduttura V S
S
x = Vt
nel tempo t = t – t0 la sezione S è attraversata dal cilindro di acqua
di altezza x = V t, cioè da un volume di acqua
Volume Area sezione x S x S v t
per cui il flusso sarà
Volume S x S v t
( S )
S V
t
t
t
m3
sec
Caso B
Il vettore velocità NON è perpendicolare alla sezione S della conduttura V S
K
H
x = Vt
Volume S HK S x cos S V t cos
Volume S v t cos
( S )
S V cos
t
t
(S ,V ) S V cos S xV
m3
sec
Def Ogni superficie piana può essere rappresentata mediante un vettore S che
ha:
1.
2.
3.
Intensità = Area della superficie
Direzione perpendicolare alla superficie
Verso, diretto all’esterno se la superficie è chiusa, arbitrario se è aperta
S
A
Def Si dice flusso di un campo vettoriale A uniforme
attraverso una superficie piana S il prodotto scalare:
( A) S x A S A cos
Flusso del campo elettrico
Esaminiamo il caso più semplice:
1° Caso
Hp: 1- Il campo elettrico è uniforme (uguale in ogni punto dello spazio)
2- La superficie è piana (il vettore superficie è definito in modo unico)
S
E
S ( E ) S x E S E cos
Il flusso del campo elettrico si misura in Nm2/C
2° Caso
Hp: 1- Il campo elettrico NON è uniforme (in generale varia da punto a punto)
2- La superficie NON è piana (il vettore superficie Non è definito in
modo unico)
E3
E2
E4
S4
S2
S3
E1
S1
n
ΦS (E) Φ1 Φ2 Φ3 .....Φn Φi
i 1
n
ΦS (E) lim Φi
n i 1
Teorema di Gauss
Ob Calcolare il flusso del campo elettrico attraverso una
superficie chiusa qualsiasi..
Consideriamo anzitutto una superficie sferica
nel cui centro è
posta una carica elettrica positiva Q
Si
+Q
+
Q
Consideriamo un “elementino” di superficie Si
il flusso del campo elettrico E attraverso Si è:
i = Si x Ei = Si Ei cos 0° = Si Ei
allora il flusso totale attraverso la sfera sarà
Ei
Ei
n
n
n
Sfera ( E ) lim i lim Si E E lim Si E Supsfera E 4 r 2
n
n
i 1
i 1
n
i 1
e poiché il campo elettrico generato da una carica puntiforme è
E k
Q
r2
avremo che
Q
1
Q
2
S ( E ) E 4r k 2 4r 4kQ 4
Q
r
4
2
Q
S E
Quindi: il flusso del campo elettrico generato dalla carica puntiforme
attraverso la superficie sferica è uguale alla carica diviso la costante
dielettrica del mezzo.
+
Q
Questo risultato è generalizzabile ad una superficie chiusa qualsiasi
S E
+
Q
Q
e ad una distribuzione qualsiasi di carica.
S
E
Q3
Q1
Q1
Q2
Q1 Q2
S E
Teorema di GAUSS
Il flusso del campo elettrico S E attraverso una superficie
chiusa qualsiasi S, è uguale alla somma algebrica di tutte e sole le
cariche Qi contenute all’interno della superficie diviso la costante
dielettrica del mezzo:
Q1 Q2 .... Qn 1 n
S E
Qi
i 1
Osservazione 1
Il flusso del campo elettrico non dipende dalla particolare superficie
considerata e quindi non dipende dalla sua forma.
S2
S1
Q1
Q2
Q3
Q4
Q1 Q2 Q3 Q4
S1 E S2 E
Osservazione 2
Il flusso del campo elettrico è dovuto esclusivamente alle cariche
interne, le cariche esterne non danno alcun contributo al flusso.
Q1
Q2
Q3
Q1 Q2
S E
Applicazioni Del Teorema Di Gauss
Campo Elettrico generato da una distribuzione sferica di carica
Dati
Corpo sferico carico uniformemente con una carica totale +Q
Obiettivo
Calcolare il campo elettrico E ad una distanza d dal centro del corpo sferico
+Q
Osserviamo che il campo elettrico
generato dalla sfera carica è un campo
radiale (la distribuzione di carica ha
una simmetria centrale), uscente (la
carica è positiva).
Campo Elettrico generato da una distribuzione sferica di carica
S
E
+Q
s E x S E S cos 0 E S
n
n
i 1
i 1
s lim n E Si E lim n Si E 4 d 2
Campo Elettrico generato da una distribuzione sferica di carica
applicando invece il teorema di Gauss avremo:
S E
Q
e poiché i due flussi devono essere uguali avremo:
E 4d 2
E
Q
0
1 Q
1 Q
Q
k
4d 2 0
40 d 2
d2
Oss. Il campo elettrico è lo stesso che si avrebbe se tutta la carica Q fosse
concentrata nel centro del corpo sferico carico.
Campo Elettrico generato da una distribuzione piana infinita di carica
Dati
Piano infinito carico uniformemente (e positivamente)
Q
Densità superficiale di carica
C/m2
costante
S
Problema Calcolare il campo elettrico in un punto P a distanza d dal
piano infinito di carica.
Il campo elettrico è
perpendicolare al piano in ogni
suo punto
E
P
E
d
E
La distribuzione di carica è
simmetrica rispetto a qualunque
perpendicolare al piano, oppure un
osservatore che si muove
parallelamente al piano vede
sempre la stessa distribuzione di
carica.
Il campo elettrico è uscente
(perché la carica è +)
Campo Elettrico generato da una distribuzione piana infinita di carica
E
cil base1 base2 sup laterale
B1
E
P
S
B2
E
base1 B1 xE1 B E1 cos 0 B E
base2 B2 xE2 B E2 cos 0 B E
n
suplaterale Ei xS i Ei S i cos 90 0
n
i 1
i 1
quindi il flusso totale è dato da
cil base1 base 2 sup laterale B E B E 0 2 B E
d’altronde per il Teor. di Gauss
cil
1
1
Qi B
i
e i due flussi devono essere uguali, quindi
1
2 B E B
allora
E
2
quindi il campo elettrico è uniforme ed ha direzione verso e intensità
costanti (in ogni punto dello spazio).
Campo Elettrico generato da una distribuzione lineare
infinita di carica
Dato un filo infinitamente lungo carico positivamente e in modo
Q
uniforme
densità lineare
C/m costante
l
il campo elettrico generato dal
filo infinito è uguale a:
E k
2
r
Campo elettrico in prossimità della superficie di un conduttore
Teorema di Coulomb
Il campo elettrico sulla superficie di un conduttore è sempre perpendicolare alla
superficie del conduttore ed ha intensità uguale alla densità superficiale di carica
diviso la costante dielettrica del mezzo nel quale si trova il conduttore
E
E
+
+
E
E
+
+
+
E
+
+
+
E
+
E
+
Il teorema è un’immediata conseguenza
del teorema di Gauss
Teorema di Coulomb
Per calcolare il campo nelle immediate vicinanze del conduttore consideriamo un
cilindro (non serve che sia reale) che racchiude un elementino di superficie S = B del
conduttore
Se il cilindro è sufficientemente piccolo
E
+
E
+
+
+
E
E
E
E
• Il campo elettrico E sulla base superiore
B1 del cilindro è perpendicolare alla base e
uniforme
• Il campo elettrico sulla base inferiore B2 è
zero (il campo all’interno del conduttore è
nullo)
• Il campo elettrico è tangente alla superficie
laterale esterna del cilindro
Teorema di Coulomb
Calcoliamo ora il flusso del campo elettrico attraverso il cilindro nei due modi studiati:
mediante la definizione di flusso e mediante il teor. di Gauss.
Calcolo il flusso secondo la definizione:
E
+
E
+
+
+
E
E
E
cil base1 base 2 sup laterale
base1 B1 xE1 B E1 cos0 B E
base2 B2 xE2 B 0 0
n
suplaterale Ei xSi Ei Si cos90 0
n
E
i 1
i 1
Teorema di Coulomb
Quindi il flusso totale attraverso il cilindro sarà il prodotto dell’area di base B per il
campo E:
cil base1 base2 suplaterale B E 0 0 B E
E
+
Calcolo il flusso mediante il teorema di Gauss:
E
+
+
+
1
1
cil Qi B
i
E
E
E
E
Il flusso è uguale alla carica totale B
contenuta nel cilindretto diviso la costante
dielettrica
Teorema di Coulomb
Uguagliando i due flussi avremo:
BE
E
+
E
+
1
B
Da cui
+
+
E
E
E
E
E












