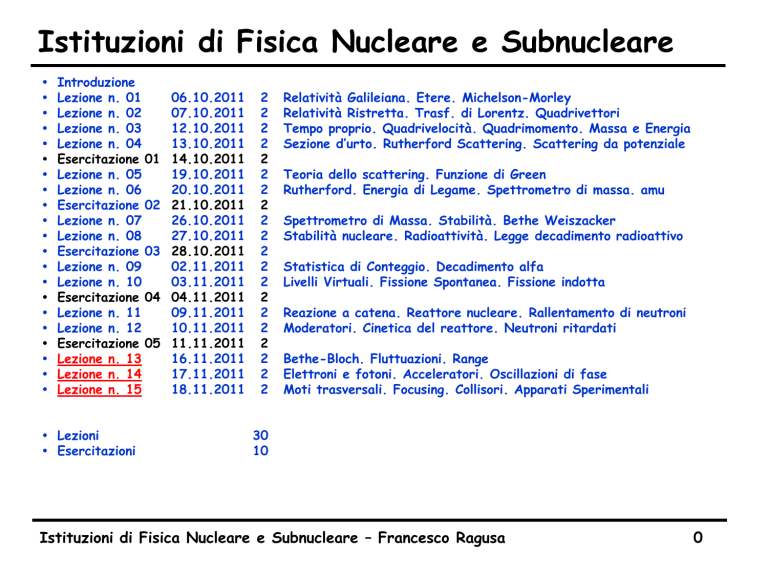
Istituzioni di Fisica Nucleare e Subnucleare
Introduzione
Lezione n. 01
Lezione n. 02
Lezione n. 03
Lezione n. 04
Esercitazione 01
Lezione n. 05
Lezione n. 06
Esercitazione 02
Lezione n. 07
Lezione n. 08
Esercitazione 03
Lezione n. 09
Lezione n. 10
Esercitazione 04
Lezione n. 11
Lezione n. 12
Esercitazione 05
Lezione n. 13
Lezione n. 14
Lezione n. 15
Lezioni
Esercitazioni
06.10.2011
07.10.2011
12.10.2011
13.10.2011
14.10.2011
19.10.2011
20.10.2011
21.10.2011
26.10.2011
27.10.2011
28.10.2011
02.11.2011
03.11.2011
04.11.2011
09.11.2011
10.11.2011
11.11.2011
16.11.2011
17.11.2011
18.11.2011
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
Relatività Galileiana. Etere. Michelson-Morley
Relatività Ristretta. Trasf. di Lorentz. Quadrivettori
Tempo proprio. Quadrivelocità. Quadrimomento. Massa e Energia
Sezione d’urto. Rutherford Scattering. Scattering da potenziale
Teoria dello scattering. Funzione di Green
Rutherford. Energia di Legame. Spettrometro di massa. amu
Spettrometro di Massa. Stabilità. Bethe Weiszacker
Stabilità nucleare. Radioattività. Legge decadimento radioattivo
Statistica di Conteggio. Decadimento alfa
Livelli Virtuali. Fissione Spontanea. Fissione indotta
Reazione a catena. Reattore nucleare. Rallentamento di neutroni
Moderatori. Cinetica del reattore. Neutroni ritardati
Bethe-Bloch. Fluttuazioni. Range
Elettroni e fotoni. Acceleratori. Oscillazioni di fase
Moti trasversali. Focusing. Collisori. Apparati Sperimentali
30
10
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
0
Istituzioni di Fisica Nucleare e Subnucleare
Introduzione
Lezione n. 01
Lezione n. 02
Lezione n. 03
Lezione n. 04
Esercitazione 01
Lezione n. 05
Lezione n. 06
Esercitazione 02
Lezione n. 07
Lezione n. 08
Esercitazione 03
Lezione n. 09
Lezione n. 10
Esercitazione 04
Lezione n. 11
Lezione n. 12
Esercitazione 05
Lezione n. 13
Lezione n. 14
Lezione n. 15
Lezioni
Esercitazioni
06.10.2011
07.10.2011
12.10.2011
13.10.2011
14.10.2011
19.10.2011
20.10.2011
21.10.2011
26.10.2011
27.10.2011
28.10.2011
02.11.2011
03.11.2011
04.11.2011
09.11.2011
10.11.2011
11.11.2011
16.11.2011
17.11.2011
18.11.2011
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
Relatività Galileiana. Etere. Michelson-Morley
Relatività Ristretta. Trasf. di Lorentz. Quadrivettori
Tempo proprio. Quadrivelocità. Quadrimomento. Massa e Energia
Sezione d’urto. Rutherford Scattering. Scattering da potenziale
Teoria dello scattering. Funzione di Green
Rutherford. Energia di Legame. Spettrometro di massa. amu
Spettrometro di Massa. Stabilità. Bethe Weiszacker
Stabilità nucleare. Radioattività. Legge decadimento radioattivo
Statistica di Conteggio. Decadimento alfa
Livelli Virtuali. Fissione Spontanea. Fissione indotta
Reazione a catena. Reattore nucleare. Rallentamento di neutroni
Moderatori. Cinetica del reattore. Neutroni ritardati
Bethe-Bloch. Fluttuazioni. Range
Elettroni e fotoni. Acceleratori. Oscillazioni di fase
Moti trasversali. Focusing. Collisori. Apparati Sperimentali
28
12
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
1
Istituzioni di Fisica Nucleare e Subnucleare
prof. Francesco Ragusa
Università di Milano
Lezione n. 13
13.11.2013
anno accademico 2012-2013
Energia trasferita in collisioni con elettroni
Una particella carica (ze) che attraversa la materia urta con gli atomi
Può cedere energia agli atomi eccitando gli elettroni
q
b
ze
Può cedere energia estraendo elettroni: ionizzazione
x
Consideriamo inizialmente un problema più semplice
ze 2
1
E =
Una particella pesante interagisce con un elettrone
4peo b2 + x 2
Il momento trasferito dalla particella all’elettrone è
dx
dx
dpy = Fy dt = Fy
= eE y
v
v
ze 2
1
Ey =
4peo b2 + x 2
b
b2 + x 2
Solo la componente verticale dà un contributo non nullo
La componente orizzontale riceve contributi di segno opposto
dalle due parti simmetriche della traiettoria
Supponiamo che l’energia trasferita all’elettrone sia molto più piccola di
quella della particella incidente
La velocità può essere considerata costante
Il momento trasferito totale si trova integrando
Dp =
+¥
ò- ¥
ze 2
b
dx
4peo [b2 + x 2 ]3/ 2 v
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
cosq
ze 2
D py =
2peo vb
3
Perdita di energia per ionizzazione
Passiamo all’energia trasferita al singolo elettrone
D p2
D E1 =
2m e
ze 2
D py =
2peo vb
Il calcolo fatto è relativo a
Un singolo elettrone ad una distanza b
Suddividiamo il materiale in gusci cilindrici
r
La densità di elettroni è ne = Z N A
é ze 2
D E1 = ê
êë4peo
ù2 2
ú
2 2
ú
û mev b
b
A
ze
dx
dN = ne 2pbdbdx
Gli elettroni nel guscio sono
L’energia trasferita agli elettroni del guscio (e quindi persa dalla particella
pesante) è
2 2
é ze
dE = D E 1dN = ê
êë4peo
ù
2
ú
n 2pbdbdx
2 2 e
ú
m
v
b
û e
Integrando sul parametro d’impatto b (e ponendo c =1 )
dE
=
dx
bmax
òb
min
é ze 2
ê
êë4peo
é e2
ù2 4pne
ú
bdb = ê
2 2
êë4peom e
ú
û me b b
ù2 4pm e z 2ne
ú
ú
b2
û
bmax
òb
min
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
2
bmax
1
2 4p m e z n e
ln
db = re
bmin
b
b2
4
Energia trasferita in collisioni con elettroni
Il calcolo fatto per ricavare DE era basato su
due ipotesi
Gli elettroni sono liberi
Si può trasferire all’elettrone una quantità
arbitraria di energia
Con queste ipotesi l’energia trasferita è
ù2 1
ú
2 2
ú
û mev b
logDE(b)
é ze 2
D E1 = ê
êë2peo
DEmax
Un calcolo esatto senza le ipotesi sopra indicate
conduce al risultato della figura
Occorre tenere conto del fatto che gli
elettroni sono legati all’atomo
Questo determina bmax
Occorre tenere del fatto che esiste
un’energia massima trasferibile
Questo determina bmin
In letteratura si trovano formule che differiscono per
le scelte fatte su bmax e bmin
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
bmin
logb
bmax
5
Parametro d’impatto: limite superiore
Discutiamo adesso i limiti di integrazione sul parametro d’impatto
Il limite superiore dipende dall’assunzione che abbiamo
fatto di considerare gli elettroni liberi
b
La forza esercitata sull’elettrone è schematizzabile
t =
come un impulso di durata t (ordine di grandezza)
v
b
b
Se inoltre teniamo conto del fatto che la velocità è
t =
1 - b2
relativistica, la durata dell’impulso viene ridotta
v
Gli elettroni non sono liberi: sono legati in orbitali atomici
Dalla teoria perturbativa dipendente dal tempo si
1
v
può verificare che se l’elettrone è in un orbitale
n<
=
caratterizzato da una frequenza n (E = hn) perchè
t
b 1 - b2
sia possibile una transizione deve essere
Pertanto deve essere b < bmax dove bmax è dato da
bmax =
v
n
1 - b2
La frequenza <n> è una opportuna frequenza media
degli orbitali esterni che caratterizza il materiale
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
6
Parametro d’impatto: limite inferiore
Consideriamo adesso il limite inferiore bmin
Possiamo stimare il limite minimo bmin come il parametro d’impatto che
corrisponde alla massima energia trasferibile
Si può calcolare che, se una particella pesante (es. protone) di velocità
b ~ 1 (e fattore relativistico g 1) collide con un elettrone, la massima
energia trasferibile all’elettrone è data da
D E = 2m e g 2 b 2
Abbiamo visto che la relazione fra parametro d’impatto ed energia
trasferita è
2 2
é ze
D E1 = ê
êë2peo
ù
1
ú
2 2
ú
û mev b
Pertanto il parametro d’impatto minimo è dato da
é ze 2
ê
êë2peo
ù2
1
ú
= 2m e g 2 b 2
2
2
ú
û m e b bmin
bmin
ze 2
=
2peo
1
2m e gb 2
Questa approssimazione (classica) risulta troppo grossolana
Produce un valore di bmin troppo piccolo
Non tiene conto della meccanica quantistica
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
7
Perdita di energia per ionizzazione
La formula trovata non tiene conto della natura quantistica della materia
Tenendo conto della meccanica quantistica il limite inferiore può essere
stimato pensando che la posizione di una particella non può essere definita
meglio della sua lunghezza d’onda di De Boroglie
bmin » l =
h
p
Sia la posizione della particella incidente che l’elettrone bersaglio hanno una
incertezza dovuta al principio di indeterminazione
Consideriamo sia il momento dell’elettrone che quello del protone
Nel sistema in cui l’elettrone è a riposo pp = mp gb
Nel sistema in cui il protone è a riposo pe = me gb
Scegliamo il bmin più grande (che corrisponde al momento più piccolo)
Ricordando bmax
bmax
bg
=
n
bmin =
h
2m e gb
bmax
2m e g 2 b 2
2m e b 2
=
=
bmin
h n
h n (1 - b 2 )
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
8
Perdita di energia per ionizzazione
Otteniamo in definitiva
2
2
dE
bmax
2me b 2
2 4p m e z n e
2 4pm e z ne
= re
ln
= re
ln
dx
bmin
b2
b2
h n (1 - b 2 )
Un calcolo che tiene conto più accuratamente degli effetti quantistici (e dello
dello spin) è stato fatto da Bethe, completato da Bloch con l’introduzione di I
2
dE
2 4p m e z n e
= re
dx
b2
2
é
ù
2
m
b
e
2ú
êln
b
êê I (1 - b 2 )
ú
ú
ë
û
vedi PDG 2008 pag. 217:
passage of particle throgh
matter
b
alta velocità: gb > 1 crescita logaritmica
dE/dx (MeV cm2/g)
I è il potenziale medio di ionizzazione (vedi diapositiva seguente)
Le unità di misura saranno discusse in seguito
Notiamo che dE/dx è funzione solo della velocità
100
Ci sono due regioni
1
bassa velocità: gb < 1 dipendenza da :
2
La formula diverge per g b
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
10
1
0.1
1
10
100
gb
9
Perdita di energia per ionizzazione
Il potenziale di ionizzazione dipende dalla sostanza
Una calcolo teorico non sempre è possibile
I
La figura mostra risultati sperimentali e calcoli teorici per b =
Z
Per bibliografia v. PDG 2008 (C. Amsler et al. Phys. Lett. B667 p. 267)
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
10
Perdita di energia per ionizzazione
Il calcolo di Bethe e Bloch è stato completato da numerosi altri calcoli
Per tenere conto di effetti trascurati
Per estenderlo ad altre regioni di velocità
Per curve e riferimenti vedi PDG 2008 pag. 267: passage of particle
throgh matter
2
dE
2 4p m e z n e
= re
dx
b2
2
é
2
m
b
d (bg )ù
e
2
êln
ú
b
êê I (1 - b 2 )
ú
2
ú
ë
û
Nelle varie regioni
Importanti interazioni
atomiche (legami)
Dipendenza da 1/b2
Risalita relativistica compensata da effetti polarizzatori (d)
Regione dominata da radiazione
di fotoni (Bremsstrahlung)
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
11
Perdita di energia per ionizzazione
2
Studiamo altri aspetti della formula dE
2 4p m e z n e
= re
Dipende solo dalla velocità della
dx
b2
particella
La stessa curva può essere utilizzata per
particelle di massa diversa
Allo stesso valore di g b corrispondono
momenti diversi: p = m g b
Ha un minimo intorno a g b 3 - 3.5 al
variare di Z da 100 a 7
La dipendenza da Z è contenuta in ne,
nell’argomento del logaritmo e in d
Introduciamo il valore di ne nella formula
2
r
dE
2 4p m e z Z
= re
rNA [ ]
ne = Z N A
dx
b2 A
A
2
é
2
m
b
d (bg )ù
e
2
êln
ú
b
êê I (1 - b 2 )
ú
2
ú
ë
û
La dipendenza della formula dal
materiale può essere resa più debole
introducendo la variabile x = xr
2
dE
2 4p m e z Z
= re
NA [ ]
2
dx
A
b
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
12
Perdita di energia per ionizzazione
L’unità di misura di x = xr è [x] = g cm-2
Con questa unità di misura si ha una debole dipendenza dal materiale
Un numero utile da ricordare è
dE/dx (MeV cm2/g)
dE
dx
: 1.5
min
MeV
g/ cm 2
100
10
1
0.1
1
10 100 g
b
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
13
Perdita di energia per ionizzazione
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
14
Ordini di grandezza per i rivelatori
Molti rivelatori di particelle sono basati sulla misura
della ionizzazione rilasciata da una particella carica
Calcoliamo l’energia rilasciata per
alcuni materiali usati normalmente
come rivelatori
1 cm Ar gassoso
1 cm scintillatore plastico
300 mm di silicio
Materiale
Materiale
rr
Ar
1.792 g/
g/ll
1.792
Scint.
Scint.
Si
dE/dx
dx rdE/ dx
dE/
1.66
1.66
0.003
1.032
1.032 g/
g/ cm
cm33 1.936
1.936
1.998
2.33
2.33 g/
g/ cm
cm33
3.5
1.519
1.519
Moltiplichiamo per la densità
Moltiplicando per lo spessore si ottiene
1 cm Ar gassoso
0.003
MeV
1 cm scintillatore plastico 1.998
MeV
300 mm di silicio
0.106
MeV
MeV
g/ cm 2
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
MeV
cm
15
Perdita di energia “limitata”
Il termine in inglese è “restricted energy loss”
In molte applicazione l’energia rilasciata viene utilizzata
per creare ionizzazione che viene poi in qualche modo
rivelata e misurata
Nei casi in cui l’energia rilasciata è molto elevata l’elettrone può ricevere tanta energia e uscire dal rivelatore
In questi casi l’energia rilasciata e l’energia rivelata sono
diverse
Per questo motivo si usa anche una
funzione che descrive il rilascio di
energia escludendo i trasferimenti
più energetici
La curva ovviamente dipende dal
“taglio”
4p N A re2m e
K =
= 0.307 MeV g- 1 cm 2
A
A = 1g/ mol
dE
dx
Z 1 é1 2m e g 2 b 2T cut
b2 æ
T cut
ç
= Kz
r 2 ê ln
1
+
A b êë2
2 çè
Tmax
I2
2
T < T cut
d-rays
E
ö
d ( bg )ù
÷
ú
÷
÷
ø
2 ú
û
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
16
Fluttuazioni nella ionizzazione
La perdita di energia di una particella è un fenomeno statistico
Le collisioni responsabili del trasferimento di energia sono casuali
Le collisioni sono indipendenti
La quantità di energia trasferita in ogni collisione è casuale
Ha una sua distribuzione di probabilità
Se considero l’energia persa da n particelle che attraversano lo stesso
spessore di materiale non tutte hanno perso la stessa energia
Il fenomeno delle fluttuazioni è stato studiato da Landau†
Successivamente da Vavilov
1 dN
La distribuzione dell’energia rilasciata D in uno
= f (D, bg, x )
N
d
D
o
spessore x di materiale è data dalla funzione
La funzione ha un picco (valore più probabile) dato da
D mp
é 2m e g 2 b 2
ù
x
= x êln
+ ln + 0.2 - b 2 - d ( bg )ú
êë
ú
I
I
û
x = 4p N A re2m e
†L.D.
Z x
r
A b2
Landau, J. Exp. Phys. (USSR) 8,p. 201 (1944)
P.V. Vavilov, Sov. Phys. JETP 5, p 749 (1957)
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
17
Fluttuazioni nella ionizzazione
La funzione che dà Dmp è simile alla funzione di Bethe –Bloch
Come nel caso della “restricted energy loss” anche nel caso dell’energia più
probabile occorre eliminare i rilasci di energia troppo grandi
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
18
Arresto delle particelle: Range
Abbiamo detto che la perdita di energia per
ionizzazione è funzione solo della velocità della
particella ( e del materiale)
dE
= z 2 f (b )
dx
Possiamo invertire la formula e scrivere
dE
dx = - 2
z f (b )
Inoltre, dal momento che
E = m g ® dE = md g
Possiamo pertanto calcolare la distanza percorsa da una particella prima di fermarsi (Range)
calcolando l’integrale (cambiando la variabile
d’integrazione da g a gb)
R ( gb ) =
R
ò0
dx = -
Arriviamo al risultato
R (E ) =
m
z2
0
p
m
ò
m
E
F
,Z
m
z2
(
1
d gb
f (b )
)
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
19
Fluttuazioni nel Range
dE/dx (MeV cm2/g)
Abbiamo visto che la perdita di energia per ionizzazione è un fenomeno
casuale soggetto a fluttuazioni
Fluttuazioni di Landau
Poichè la quantità di energia rilasciata fluttua anche lo spazio percorso prima
di arrestarsi fluttua
Non tutte le particelle di uguale energia si arrestano dopo aver percorso
lo stesso spazio
Si può calcolare la distribuzione dello spazio percorso
Infine, osserviamo che man mano che la particella rallenta la sua perdita di
energia per unità di percorso aumenta
Molta energia viene rilasciata alla fine del percorso (picco di Bragg)
100
10
1
0.1
1
10
100
gb
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
20
Istituzioni di Fisica Nucleare e Subnucleare
prof. Francesco Ragusa
Università di Milano
Lezione n. 14
14.11.2013
anno accademico 2012-2013
Perdita di energia per gli elettroni
A basse energie gli elettroni perdono
energia con meccanismi simili a quelli
visti per le particelle pesanti
Ci sono tuttavia differenze
Si deve tenere conto dell’identità
delle particelle
L’approssimazione che l’energia persa
sia trascurabile non è sempre adeguata
A bassa energia la traiettoria
dell’elettrone può essere non rettilinea
2
dE
2 4p m e z n e
= re
g : 1 dx
b2
g? 1 -
dE
= re2 4pme z 2ne
dx
gb : 103 ® E : 500 MeV
é me b 2 1
1ù
êln
- ln 2 + ú
êë 2I
2
2ú
û
radiazione
ionizzazione
é me
3
1
1
1ù
êln
ú
+ ln
ln
8
+
4 1 - b2 2
16 ú
êë 2I
û
Occorre tenere conto della radiazione già ad energie relativamente basse
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
22
Perdita di energia per radiazione (elettroni)
Quando l’energia dell’elettrone è molto maggiore della massa a riposo ( Eme ) diventa
importante il meccanismo di perdita di
energia per radiazione
La radiazione dipende da Z2 e da E
La ionizzazione dipende da Z e da lnE
Si definisce energia critica il valore Ec per il
quale la perdita per ionizzazione e quella per
radiazione sono uguali
elettrone - positrone
fotone
dE
dE
(E c )
(E c )
=
dx
dx
rad
ion
Approssimativamente
610 MeV
Ec =
Z + 1.24
710 MeV
Ec =
Z + 0.92
solidi
gas
I fenomeni della radiazione e della creazione
di coppie sono strettamente legati
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
23
Perdita di energia per radiazione (elettroni)
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
24
Perdita di energia per radiazione (elettroni)
L’energia irraggiata appare sotto forma di raggi X e prende il nome di
Bremsstrahlung
Ha uno spettro continuo
Ė la radiazione emessa dagli elettroni nei tubi a raggi X
La distanza percorsa nel materiale dopo la quale l’energia dell’elettrone è
ridotta a 1/e del valore iniziale prende il nome di lunghezza di radiazione
Xo =
716.4A
Z (Z + 1 )ln [287 /
Z]
g cm-
2
La perdita di energia per radiazione
si può scrivere come
-
dE
E
=
dx
Xo
Ciò significa che l’energia dell’elettrone
varia (diminuisce) secondo la legge
E = E o exp [- x / X o ]
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
25
Bremsstrahlung
La radiazione emessa ha le seguenti caratteristiche
A bassa energia
L’intensità della radiazione emessa ha un massimo
in una direzione perpendicolare alla direzione
del moto dell’elettrone
La radiazione è polarizzata: il vettore elettrico
della radiazione (onda) emessa è prevalentemente
parallelo alla velocità
Ad alta energia
me
q:
Il fotone è emesso in avanti
Ee
L’angolo di emissione non dipende
dall’energia del fotone
Il vettore elettrico è prevalentemente
perpendicolare al piano (elettrone-fotone)
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
E
E
q
26
Passaggio dei fotoni nella materia
L’interazione dei fotoni con la materia provoca sostanzialmente
3 tipi di fenomeni
Effetto fotoelettrico
Estrazione di elettroni legati
Diffusione da parte degli elettroni
Nell’ipotesi che gli elettroni siano considerati liberi
Produzione di coppie elettrone-positrone
Sono 3 processi molto complessi e molto diversi tra di loro
L’importanza relativa dei 3 processi dipende sostanzialmente da
L’energia del fotone
Numero atomico del materiale assorbitore
Anche nel caso dei fotoni si ha una legge di assorbimento di tipo esponenziale
N (x ) = N o exp [- mx ]
m=
r
N s
A A
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
27
Effetto fotoelettrico
IN
IM
Ci sono più soglie IL
IK
E
Il processo è possibile solo se l’energia del
fotone è maggiore dell’energia della shell
E g > I K ,L K
L’elettrone emesso ha un’energia
sezione d’urto (barn)
In questo processo il fotone riesce a trasferire all’elettrone atomico una
quantità di energia sufficiente a ionizzarlo
Ovviamente questo processo ha una soglia
L’energia di legame degli elettroni in un
Z5
atomo complesso ha diversi valori discreti
s :
legati alla struttura a shell:
E g3.5
10
Piombo
103
102
101
100
10
105
106
Eg (eV)
107
108
Te = E g - I X
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
28
Effetto fotoelettrico
Il valore delle energie a cui si hanno le discontinuità
(Z - s )2
è dato approssimativamente dalla relazione
E X = R hc
2
n
Rhc = 13.605 eV è l’energia di Rydberg
n numero quantico principale
K n = 1 s = 3
s costante di schermo
L n = 2 s = 5
Dipendono dalla shell
L’orbitale lasciato vuoto dal processo viene successivamente riempito da un
elettrone più esterno con emissione di radiazione
Radiazione di fluorescenza
Ė anche possibile che nel processo di riempimento di un orbitale interno da un
elettrone esterno l’energia in eccesso venga emessa come energia cinetica di
un elettrone esterno espulso anch’esso
Effetto Auger: elettroni monocromatici
Ad esempio
Effetto fotoelettrico su shell K
Tauger = E K - E L - E M
Riempita da elettrone della shell L
Emissione di un elettrone della shell M
L’effetto fotoelettrico è trascurabile per energie maggiori di 1 MeV
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
29
Scattering Compton
Lo scattering Compton è l’interazione di un fotone con un elettrone debolmente
legato che può essere considerato libero
Può essere visto come l’urto di un fotone
su un elettrone inizialmente a riposo
E g¢
Eg
Ė facile verificare che
E g¢ = E g - T e =
Eg
k =
me
Eg
1 + k (1 - cos q )
sezione d’urto (barn)
q
Ee
Piombo
102
s :
101
Z
Eg
100
10-1
10-2
L’effetto Compton è il processo dominante
102
nella regione fra 0.1 e 10 Mev
Ad energie molto basse è importante lo scattering
Rayleigh: interazione coerente con tutto l’atomo
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
10
106
Eg (eV)
108
1010
30
Produzione di coppie
q:
me
Ee
L’energia k si suddivide fra i due elettroni
0.5 GeV
sezione d’urto (barn)
Come abbiamo detto la produzione di coppie è molto simile alla Bremsstrahlung
La produzione di coppie deve avvenire in presenza di un campo elettrico
intenso (ad esempio il campo elettrico di un nucleo)
Nello spazio vuoto non è cinematicamente possibile
La sezione d’urto cresce rapidamente appena
superata la soglia
Piombo
Ad alta energia gli elettroni hanno un momento 102
che forma con la direzione del fotone un angolo
s : Z2
101
100
10-1
0.1 GeV
10-2
102
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
10
106
Eg (eV)
108
1010
31
Assorbimento di fotoni
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
32
Dosimetria
La perdita di energia è importante anche per i suoi effetti biologici
La dose è la quantità di energia depositata per unità di massa
La sua unità di misura è il Gray
1Gy = 1J kg- 1 = 6.25 ´ 1012 MeVkg-
1
L’effetto della radiazione dipende non solo dalla quantità di energia rilasciata
ma anche dalla densità della radiazione depositata
Si usa la dose equivalente per avere una stima migliore del danno biologico
causato dalla distruzione nelle cellule di legami chimici e molecolari
Il rischio più importante costituito dalle mutazioni
che possono originare cancro
L’unità di misura della dose equivalente è il Sievert (Sv)
1Sv =
å
wR ´ Gy
Il fattore wr ha una origine empirica
Tiene conto del rischio causato da
lunga esposizione a diversi tipi di
radiazione
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
33
Acceleratori di particelle
Per accelerare una particella carica occorre un campo elettrico
0 KV
-
100 KV
+
-
200 KV
+
-
300 KV
+
-
400 KV
+
-
500 KV
+
-
600 KV
+
Poco pratico:
Per raggiungere elevate energie occorrono tensioni elevatissime
1 milione di volt per 1 MeV
LHC avrà energie di 7 TeV
1 TeV = 1012 eV = 106 MeV
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
34
Acceleratori di particelle
Si fa in modo che il potenziale acceleratore viaggi con la particella
-50 KV
-
-50
+50 KV
+
-
-50
+50 KV
KV
+
-
-50
+50 KV
KV
+
-
-50
+50 KV
KV
+
-
-50
+50 KV
KV
+
-
+50 KV
+
Il potenziale che viaggia è un’onda elettromagnetica
Il campo elettrico deve essere longitudinale
La velocità dell’onda e della particella devono
essere uguali
Cavità risonanti: immagazzinano tanta energia
( r ~ |E|2 )
Limitato dall’emissione di elettroni dalle pareti
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
35
Acceleratori lineari
Per costruire un acceleratore si possono disporre tante cavità
acceleratrici in serie ( Acceleratore Lineare )
e
e
L’Acceleratore Lineare PEP II di SLAC (Stanford, California)
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
36
Acceleratori Circolari
acceleratore lineare
dipoli magnetici
cavità acceleratrici
Anello con alto vuoto ( Beam Pipe)
Un campo magnetico perpendicolare al
disegno confina le particelle in una orbita
circolare
Le particelle sono preaccelerate da un
acceleratore lineare (LINAC)
Vengono iniettate nell’anello dell’acceleratore:
Il campo magnetico viene regolato in
modo che
p = 0.3 BR
Le particelle seguono un’orbita circolare
Una cavità accelera le particelle ad ogni
attraversamento
Il campo magnetico aumenta in fase con
l’aumento di energia: sincrotrone
La cavità compensa l’energia radiata
Essenziale per accelerare elettroni
Per raggiungere energie molto elevate
si utilizzano molte cavità
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
37
Moto in campo magnetico
L’equazione del moto di una particella carica in un campo magnetico è
dp
= ev´ B
dt
In relatività ristretta la quantità di moto
si può scrivere come pc = e v/c con
e l’energia della particella
v la sua velocità
L’equazione del moto diventa
dp
1 de
e dv
= 2
v+ 2
= ev´ B
dt
c dt
c dt
Moltiplicando per v si ottiene ( v è perpendicolare a dv e a vB )
de
= 0
dt
L’equazione del moto diventa pertanto
dv
= v ´ Wv
dt
Wv =
eB 2
c
e
Cioè la velocità precessa con velocità
angolare Wv
Se v è perpendicolare a B la traiettoria
della particella è una circonferenza percorsa in un tempo T = 2p/Wv
Per trovare il raggio della circonferenza
2p R
vT
v
= v® R =
=
T
2p
Wv
ve
p
be
=
pc
R =
R
=
eB
eBc 2
Esprimendo il momento pc in GeV, il raggio
in metri e il campo magnetico in Tesla
Ritroviamo il risultato che il campo magnetico non fa lavoro e l’energia si
conserva
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
pc = 0.3 R B
38
Acceleratori Circolari
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
39
Cavità acceleratrici
Consideriamo un acceleratore con una sola
cavità
LEP: C = 26.6589 Km
Quando una particella entra nella cavità
trova un campo elettrico longitudinale
Il campo elettrico è un’onda elettromagnetica che viaggia con la stessa
velocità della particella
All’interno di una cavità il campo elettrico
varia in funzione del tempo
Ad esempio, all’ingresso della cavità
E (t ) = E o cos wot
La frequenza di rivoluzione della particella è
frev =
1
bc
=
T
C
La particella deve trovarsi in fase con
l’onda elettromagnetica
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
40
Traiettoria sincrona
La condizione che la particella entri nella
cavità con la stessa fase rispetto alla RF
impone che la frequenza nella cavità sia
un multiplo della frequenza di rivoluzione
fRF = h ×frev
LEP
LHC
f r ev (KHz)
11.2455
11.2455
f R F (KHz)
352 209.060
40 000
h
31320
3564
Il campo accelerante visto dalla particella
dipende dalla fase all’ingresso
E f = E o cos f
L’energia guadagnata dalla particella alla
fine del suo percorso all’interno della
cavità è pertanto
D E = Eo ×L cos f
Eo è il campo acceleratore massimo della
cavità e viene espresso in MV/m
La traiettoria sincrona è quella che consente alla particella di entrare nella cavità sempre con la stessa fase
Nel LEP gli elettroni sono fortemente
relativistici ( E ≈ 45 GeV, g ≈ 105 )
Anche in LHC i protoni sono molto
relativistici ( E = 7 TeV, g 7.5 103 )
La variazione di energia di una particella
lungo l’orbita ( DE 10-100 MeV ) non può
cambiare la velocità al punto di alterare
la fase
C
T =
bc
dT
db
= T
b
2
1 - b2
1 mc 2
- 2b
dE = db
2 1 - b2 1 - b2
dE
db
= g 2b 2
E
b
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
E = mc g =
mc 2
DT
1 DE
= - 2 2
T
b g E
41
Oscillazioni di Fase
La fase può variare a causa della variazione del raggio dell’orbita
C
T =
bc
Pertanto
-p
DT
DC
DR
=
=
T
C
R
Il raggio è determinato dal campo magnetico e dal momento ( energia, E = p )
dell’elettrone
Dg
E
p
f
fs
f
p = 0.3 ×B ×R
DT
DE
=
T
E
Dp
p
Esiste una intervallo di fasi che permette
il funzionamento stabile della macchina
Ad esempio fs
Una particella in anticipo rispetto fs:
È soggetta ad un campo maggiore
Acquista più energia
Percorre una circonferenza maggiore
Al giro successivo è in ritardo
Viceversa, una particella in ritardo:
È soggetta ad un campo minore
Acquista meno energia
Percorre una circonferenza minore
Al giro successivo è in anticipo
Le particelle pertanto oscillano intorno al
punto di stabilità fs
La regione di stabilità è individuata nel
piano Dg - f
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
42
Istituzioni di Fisica Nucleare e Subnucleare
prof. Francesco Ragusa
Università di Milano
Lezione n. 15
15.11.2013
anno accademico 2012-2013
Moti trasversali
Per descrivere il moto di una particella in
un acceleratore circolare si utilizzano le
seguenti convenzioni
In un dipolo reale il campo non è perfettamente uniforme
l’equazione del moto
d 2x
= - K x ×x
ds 2
z
z
s
x
da
R
ds=Rda
Oltre al moto circolare le particelle hanno dei moti trasversali
Il campo magnetico è fornito da dipoli
magnetici
Kx =
1 ¶ Bz
BR ¶ x
Kx =
1
b x2
x
La soluzione è simile a un moto armonico
x (s ) =
bx ex sin (y (s ) + l )
y (s ) =
ds
ò bx (s )
Considerazioni analoghe per il moto lungo
z determinato dalla componente Bx
I moti trasversali sono pertanto moti armonici determinati dalle disuniformità del
campo magnetico tramite le funzioni
bx(s) e by(s)
LEP 45 m < b < 135 m
LHC 40 m < b < 180 m
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
44
Oscillazioni di betarone
Nella loro orbita le particelle compiono
pertanto un moto oscillatorio, le oscillazioni di betatrone
Le oscillazioni sono governate dalle
funzioni b
ds
(s )
ò bx
y (s ) =
L’avanzamento di fase complessivo in una
rivoluzione completa è
Dy =
ds
(s )
òÑbx
Dy
Q =
2p
Q è detto “tune” (orizzontale o verticale) e
rappresenta il numero delle oscillazioni nel
corso di una rivoluzione completa
LEP : 60 < QH ,V < 100
Q dipende dalle funzioni b e quindi dai
gradienti magnetici
Può essere modificato modificando le
correnti dei magneti
Per una macchina sia stabile occorre che
Q non sia un numero intero o razionale
In questo caso infatti una particella
ripasserebbe con la stessa fase
attraverso inevitabili difetti magnetici
che farebbero crescere l’ampiezza delle
oscillazioni fino alla perdita del fascio
La seguente condizione di risonanza deve
essere evitata
lQH + mQV = n
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
45
Risonanze
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
46
The LHC tune diagram
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
47
Focalizzazione
È importante contenere l’ampiezza dei
moti trasversali: quadrupoli
z
S
B x = - K x ×z
N
B z = - K z ×x
F
F
B
N
v
v
S
Si può ottenere una funzione focalizzante
in entrambe le direzioni utilizzando due
quadrupoli ( uno F, uno D) posti in serie e
separati da una sezione dritta vuota (O)
x
F
F = ev´ B
B
La Forza di Lorentz che un campo di
questo tipo esercita su una particella
positiva è
defocalizzante in direzione x
focalizzante in direzione z
O
D
O
La struttura FODO è detta “a Gradiente
Alternato” o “Focalizzazione Forte”
In un quadrupolo il campo magnetico è
nullo al centro (e solo al centro)
la traiettoria centrale è definita dai
centri dei quadrupoli
Beam Orbit Monitors ( BOM ) sono
montati sui quadrupoli
Una particella che non attraversa un quadrupolo al centro è soggetta ad un ulteriore campo dipolare
Il campo dei quadrupoli contribuisce alle
funzioni b
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
48
“Strong Focusing”
La focalizzazione forte permette di ridurre l’ampiezza delle oscillazioni
trasversali di circa un fattore 100, quindi da metri a centimetri
Le camere a vuoto e i magneti possono essere ridotti di conseguenza
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
49
Energia e Campo Magnetico
La relazione fra momento e campo magnetico è (per gli elettroni di LEP p = E)
p = 0.3 ×B ×R
Tenendo conto delle variazioni di B lungo l’orbita
ds
p = 0.3 ×B (s ) ×
da
òÑpd a
= 0.3ò
ÑB (s )ds
Definendo il momento medio
p º
1
2p
òÑpda
E =
p =
0.3
ÑB (s )ds
2p ò
Il sistema magnetico di LEP (dipoli, quadrupoli, sestupoli) è conosciuto con
elevata precisione (relativa):
Modelli per la variazione del campo nelle varie posizioni
Durante il funzionamento dell’acceleratore vengono registrate continuamente:
La corrente dei magneti
La temperatura dei magneti
Le letture delle sonde NMR
… molto altro …
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
50
Bersaglio Fisso e Collis(ionat)ori
Gli acceleratori vengono utilizzati con due modalità di funzionamento
Fascio estratto: esperimenti a bersaglio fisso
Collider: collisione di fasci
Storicamente la modalità con fascio estratto è stata la prima a essere
utilizzata
La differenza principale fra le due modalità è la massima energia disponibile
per produrre nuove particelle
Fondamentale nella scoperta di nuovi fenomeni
Vediamo qual’è l’energia minima che deve avere un protone pre produrre una
particella di massa MX
In una collisione di un protone fascio con un nucleone bersaglio si ha
p+ N ® N + X
Tralasciamo la conservazione di numeri quantici (carica, numero barionico,…)
Dalla cinematica
s = ( p1 + p2 )2 = ( p3 + pX )2
La soglia per la produzione corrisponde al valore di s per il quale nel centro di
massa della particelle 3 e della particella X esse sono a riposo
L’energia è stata usata solo per produrre massa (zero energia cinetica)
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
51
Bersaglio Fisso e Collisori
Il valore di s corrispondente è
s = (m 3 + M X )2
Per un esperimento a bersaglio fisso si ha
s = ( p1 + p2 )2 = m 12 + m 22 + 2m 2E 1
L’energia minima per la produzione della massa MX è pertanto
E1 =
(m 3 + M X )2 - m 12 - m 22
2m 2
L’energia minima per la produzione della
massa MX è pertanto
m + MX
E1 = 3
2
E1 :
Ebeam (GeV)
Per un esperimento con fasci in collisione
si ha
s = ( p1 + p2 )2 = (E 1 + E 2 )2 = 4E 12
M X2
E1 :
2m p
MX
2
Con i fasci in collisione, a parità di energia
del fascio, si producono masse più elevate
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
MX (GeV)
52
La luminosità
Abbiamo visto che in un collisore due fasci di
particelle sono fatti circolare in direzione opposta
e fatti collidere in opportune regioni (punti di
intersezione) dove sono installati i rivelatori
I fasci sono raggruppati in pacchetti (bunches):
n1 e n2 sono il numero di particelle nei bunches
dei due fasci di area (sezione) S
La frequenza delle collisioni dei due bunches è f
Se s è la sezione d’urto di un dato processo,
il numero di eventi di quel processo prodotti
al secondo è
n
dN
Si definisce
= n1f 2 s
Luminosità Integrata
dt
S
n
L = n1 f 2
S
Si definisce Luminosità
Si misura in cm-2s-1
In un dato esperimento il numero
di eventi prodotti è
N =
ò dN =
ò n1f
ò L dt
La luminosità integrata è l’inverso
di una sezione d’urto; si misura in
nb-1, pb-1…
In un esperimento, nota la luminosità integrata la sezione d’urto è
n2
s dt = s ò L dt
S
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
s = N/
ò L dt
53
Apparati Sperimentali
In una interazione vengono prodotte:
Particelle cariche
Adroni (interazione forte)
Leptoni carichi (interazione
elettromagnetica)
Particelle neutre
Fotoni
Adroni (neutroni, kaoni)
Leptoni neutri: neutrini (invisibili)
Funzioni del rivelatore
Misura della quantità di moto
delle particelle cariche
Misura dell’energia delle
particelle neutre
Identificazione
Elettroni,fotoni
Adroni
Muoni
rivelatore adroni
rivelatore muoni
B
tracciatore
rivelatore elettroni/fotoni
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
54
Esempio: Interazione e+e- in ALEPH
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
55
The first ATLAS Collision
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
56
ATLAS Beam Halo Event (November 2009)
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
57
Dati dai rivelatori
Come funzionano i rivelatori:
I rivelatori producono Mbytes di
informazioni al secondo
Le informazioni vengono raccolte ed
elaborate da computers
Si possono produrre “immagini
virtuali” dell’evento
Si analizzano i dati per misurare
grandezze fisiche
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
58
Immagini virtuali
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
59
Gli Esperimenti: ATLAS
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
60
Istituzioni di Fisica Nucleare e Subnucleare
prof. Francesco Ragusa
Università di Milano
Lezione n. 12
25.11.2010
anno accademico 2012-2013
Tracking
Per Tracking si intende la ricostruzione della
traiettoria di particelle cariche (tracce) negli
esperimenti di fisica delle particelle elementari
Lo scopo è misurare (lista non completa )
segno della carica
F = qv´ B
momento (campo magnetico)
v
B
p = 0.3·B·R
Identificazione delle particelle (massa);
non necessariamente lo stesso rivelatore
tagging di vita media
vertice secondario
vertice primario
p = mo g b
parametro d’impatto
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
62
Moto in campo magnetico
Abbiamo già visto che in un campo magnetico l’energia di una particella non
cambia
d 2r
dr
mo g 2 = e ´ B
L’equazione del moto è
dt
dt
Untilizzando come variabile la
lunghezza l della traiettoria
dl = vdt
percorsa invece di t
Si ottiene
d 2r
dr
m o gv 2 = e ´ B
dl
dl
d 2r
e dr
=
´ B
p dl
dl 2
Nel caso di un campo magnetico non omogeneo
B(l) varia lungo la traiettoria
la traiettoria r(l) si trova risolvendo
un’equazione differenziale
Nel caso di B omogeneo
La soluzione è un’elica
vz
B
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
vs
v
63
Spettrometri magnetici
Molti esperimenti di fisica delle particelle elementari con acceleratori hanno
uno spettrometro magnetico per misurare il momento delle particelle cariche
Si utilizzano prevalentemente 2 configurazioni
campo magnetico solenoidale
campo magnetico dipolare
Campo dipolare
Campo solenoidale
x
B
B
x
z
y
Simmetria cilindrica
Deflessione nel piano x - y (r - f)
I rivelatori sono disposti su gusci
cilindrici (chiusi da “tappi”)
Misura della traiettoria curva nel
piano r - f a fissati r
z
y
Simmetria rettangolare
Deflessione nel piano y - z
I rivelatori sono disposti su piani
paralleli perpendicolari a z
Misura della traiettoria curva nel
piano y - z a fissati z
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
64
Tracking Systems: ATLAS
Pixel Detector
3 barrels, 3+3 disks: 80106 pixels
barrel radii: 4.7, 10.5, 13.5 cm
pixel size 50400 mm
srf= 6-10 mm sz = 66 mm
SCT
4 barrels, disks: 6.3106 strips
barrel radii:30, 37, 44 ,51 cm
strip pitch 80 mm
stereo angle ~40 mr
srf= 16 mm sz = 580mm
TRT
barrel: 55 cm < R < 105 cm
36 layers of straw tubes
srf= 170 mm
400.000 channels
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
65
Tracking Systems: CMS
Outer
Barrel –TOBInner Barrel
–TIBInner Disks
–TID-
Pixel
End cap –
TEC-
2,4
m
Pixel Detector
2 barrels, 2 disks: 40106 pixels
barrel radii: 4.1, ~10. cm
pixel size 100150 mm
srf= 10 mm sz = 10 mm
Internal Silicon Strip Tracker
4 barrels, many disks: 2106 strips
barrel radii:
strip pitch 80,120 mm
srf= 20 mm sz = 20 mm
External Silicon Strip Tracker
6 barrels, many disks: 7106 strips
barrel radii: max 110 cm
strip pitch 80, 120 mm
srf= 30 mm sz = 30 mm
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
volume 24.4 m3
66
Tracking Systems: ATLAS & CMS
ATLAS
CMS
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
67
Misura del momento
Il momento della particella è proiettato lungo 2 direzioni
Nel piano r - f si misura
il momento trasverso p
l
P^ = P cos l = 0.3BR
Nel piano r - z si
misura l’angolo di dip l
r
z
l
z
Ordini di grandezza
P^ = 1GeV
B = 2T
R = 1.67 m
P^ = 10GeV
B = 2T
R = 16.7 m
Assumiamo una lunghezza di 1 m
s
s = R (1 - cos a )
2a
P^
r
Sagitta e momento
La misura della sagitta e della lunghezza della traiettoria permettono
la misura di R (e quindi di p )
R
L
2a =
R
r
P
PL
r
f
P^ = 1GeV
s = 7.4 cm
P^ = 10GeV
s = 0.74 cm
a2
L2
s » R
=
2
8R
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
68
Misura del momento
Una volta misurato il momento trasverso e l’angolo di dip il momento totale è
P =
P^
0.3BR
=
cos l
cos l
L’errore sul momento è
P
¶P
= ^
¶R
R
¶P
= - P^ tan l
¶l
2
2
D
R
æD P ö
æ
ö
÷
÷
çç
= çç
+ ( tan l D l )2
÷
÷
è P ø
è R ø
Ė necessario studiare
L’errore sul raggio misurato sul piano di curvatura r - f
L’errore sull’angolo di dip misurato sul piano r - z
Commento:
In un collider adronico l’enfasi è sul momento trasverso
I processi elementari fra i partoni non sono a riposo nel sistema di
laboratorio
La conservazione dell’impulso per vincolare grandezze non misurate è
utilizzabile solo nel piano trasverso
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
69
Misura del momento
Vediamo come l’errore sul momento è legato alla
precisione con cui vengono misurati le coordinate
della traiettoria (risoluzione spaziale)
Ritornando alla sagitta
Assumiamo di avere 3 misure: y1, y2, y3
y1
Otteniamo
a2
L2
y + y2
s = y3 - 1
2
3
ds =
dy : dy
2
s » R
Combinando i risultati ottenuti
L2 dp
= dy
8R p
dp
8R
= 2 dy
p
L
2
=
8R
R =
dp
dR
=
p
R
y3 s
y2
R
2
ds =
p
0.3B
L dR
: dy
8R R
dp
8p
=
dy
p
0.3BL2
2a =
2a
s = R (1 - cos a )
dp
8dy
=
p2
0.3BL2
Aspetti salienti dell’errore sul momento
L’errore percentuale è proporzionale al momento stesso
È inversamente proporzionale a B
È inversamente proporzionale a 1/L2
È direttamente proporzionale alla risoluzione spaziale dy
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
L
R
70
Equazione dell’elica
In forma parametrica l’elica è descritta
dalle equazioni
hs cos l
é
x (s ) = x o + R êcos F o +
R
ë
(
hs cos l
é
y (s ) = yo + R êsin F o +
R
ë
(
)
)
R (m ) =
p^ (GeV )
0.3B (T )
ù
- cos F o ú
û
PL
ù
- sin F o ú
û
l
z (s ) = zo + s sin l
B
l è l’angolo di “dip”
h =±1 è il senso di rotazione sull’elica
La proiezione sul piano x-y plane è una
circonferenza
2
r
P
(x o , y o )
2
(x - xo + R cos F o ) + (y - yo + R sin F o ) = R
xo e yo sono le coordinate a s = 0
Fo è anche legato alla pendenza della
tangente alla circonferenza a s = 0
P^
Fo
2
R sin F o
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
R cos F o
71
Equazione dell’elica
Per ricostruire la traiettoria si posizionano piani
di misura lungo il percorso della particella
Usualmente si considerano le proiezioni
su due piani
perpendicolare a B (x,y): circonferenza
linea retta
contenente B (x,z), (y,z) or (r,z)
(x 2, y2, z 2 )
Nel piano che contiene B (per esempio il piano
y - z) la traiettoria è una funzione periodica di z
hs cos l
é
y (s ) = yo + R êsin F o +
R
ë
y (z ) = yo
(
é
+ R êsin (F
ëê
o
+
)
ù
- sin F o ú
û
(x1, y1, z1 )
s =
z - zo
sin l
h (z - zo )
ù
- sin F o ú
ú
R t an l
û
)
Tuttavia, per momenti elevati, ad esempio R tanl >> ( z-zo ),
assumendo per semplicità h = 1, Fo = 0
y (z ) » yo +
1
(z - zo )
t an l
y (z ) = yo + ct an l (z - zo )
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
linea retta
72
The Helix Equation
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
73
Rivelatori a semiconduttore
Si realizzano rivelatori di posizione utilizzando semiconduttori
si utilizza silicio con tecniche di fabbricazione di circuiti integrati
spessore tipico 300 mm
alluminio
Un tipico esempio:
materiale n
passivazione di SiO2
giunzione p-n
implantazioni p
implantazione di silicio p+
passo tipico 50 mm
giunzione p - n
silicio di tipo n+
silicio di tipo n
inversamente polarizzata
contatto ohmico
regione senza cariche mobili
(depleteted region)
Una particella carica che attraversa la regione svuotata
produce ionizzazione
Vo
la ionizzazione si muove sotto l’effetto del campo
elettrico e viene raccolta sugli elettrodi
+
La posizione dell’elettrodo individua la posizione
della traiettoria
Al deposit
implantazione n+ passivazione etching
Realizzazione dei contatti
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
74
Microstips detectors, Pixel detectors
A seconda delle dimensioni delle implantazioni si hanno due tipi di rivelatori
Rivelatori a microstrip
dimensioni tipiche
passo 50 mm
lunghezza 5 cm
Rivelatori a pixel
dimensioni tipiche
80 mm 80 mm
entrambe le direzioni con la
stessa precisione
50 mm 400 mm
una direzione più con maggiore precisione
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
75
Interconnessione
Uno dei problemi più complessi con i rivelatori a Pixels è la connessione
collegare i singoli pixels ai canali di elaborazione elettronica
Tecnica del Bump bondig
sensori
elettronica di lettura
bumps
chip flip
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
76
Moduli
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
77
Sistema
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
78
Vecchi rivelatori
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
79
Risoluzione spaziale
Qualè la risoluzione spaziale di un rivelatore di questo tipo ?
Una particella che lo attraversa interessa
una strip
la posizione della strip è xi
Sono misurate con la stessa posizione
tutte le particelle che attraversano il
rivelatore ad una posizione compresa fra
sx =
50
» 14 mm
12
D
D
D
£ x £ xi +
xi 2
2
2 xi
D
L’errore di misura è uniformemente distribuito
xi +
2
Il valor medio della distribuzione è ovviamente xi
x max
1 x max
dN
x = ò
f (x )xdx =
xdx
=
x
i
dx
x min
D òx min
xi -
La varianza della distribuzione è
s x2
=
x max
òx
f x
(
min
x- x
)(
)2
1
dx =
D
ò-
+ D2
D
2
1
D
D2
x dx =
12
2
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
xi -
D
2
xi
xi +
D
2
80
x
Migliorare la risoluzione
La risoluzione può essere migliorata utilizzando la suddivisione della carica
La carica rilasciata si suddivide fra due strip adiacenti
Il rapporto con cui si suddividono dipende
dalla posizione fra le due strip
no charge sharing: 1 hits
charge sharing: 2 hit
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
81
Alcuni membri del nostro gruppo
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
82
Istituzioni di Fisica Nucleare e Subnucleare
prof. Francesco Ragusa
Università di Milano
Lezione n. 18
27.11.2008
anno accademico 2012-2013
Istituzioni di Fisica Nucleare e Subnucleare
prof. Francesco Ragusa
Università di Milano
Lezione n. 19
28.11.2008
anno accademico 2012-2013
Istituzioni di Fisica Nucleare e Subnucleare
prof. Francesco Ragusa
Università di Milano
Lezione n. 20
05.12.2008
anno accademico 2012-2013
Perdita di energia per ionizzazione
Veniamo al trattamento quantistico della perdita di energ
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
86
Interludio: velocità del centro di massa
In relatività ristretta occorre ridefinire la velocità del centro di massa
Consideriamo un gruppo di n particelle caratterizzate da quadrimomenti pk
Le possiamo considerare un’unica particella caratterizzata da
P = p1 + K + pn
E = E1 + K + En
Ricordiamo che P m =
(M g
p = p1 + K + pn
M 2 = P 2 = E 2 - p2
M gb ). Allora la particella fittizia ha velocità
E
M
Il centro di massa si muove solidalmente con la particella fittizia.
La sua velocità è b.
Consideriamo adesso l’urto di due particelle di cui una a riposo (sistema di
laboratorio)
la velocità del centro di massa in questo sistema è
g cm =
E
M
=
p2 = 0
b=
p
E
b cm =
p
E
g =
=
p2 = 0
p1
E1 + m 2
E1 + m 2
(E 1 + m 2 )2 - p12
=
E1 + m 2
m 12 + m 22 + 2m 2E 1
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
87
Interludio:massimo momento trasferito
Consideriamo adesso l’urto di una particella pesante (un protone) con una
leggera (un elettrone)
Nel loro centro di massa le particelle hanno lo stesso momento
e si urtano frontalmente
Il massimo momento trasferito si ha quando l’elettrone “rimbalza” indietro
In questo sistema il momento dell’elettrone si trova con la trasformazione di
Lorentz dal laboratorio (dove l’elettrone è fermo) al centro di massa
me
Indichiamo con g* e b* la velocità del centro di massa
<< 1
mp
g* =
E p + me
m p2 + m e2 + 2m e E p
» g
b* =
pp
» b
E p + me
Otteniamo (v. PDG, Kinematics p. 275)
æE e* ö
çç ÷
÷=
çç * ÷
÷
÷
çè pe || ø
÷
æ g*
æ g*
öæm e ö
æ me g * ö
- g *b * ö
- g *b * ÷
Ee ö
æ
÷
÷
çç
ç
çç
÷
÷
÷
çç ÷
çç ÷
çç
÷
÷
÷
÷
=
÷
=
çç * *
ç
÷
÷
÷
÷
÷
*
* *
*
ç
*
*
p
0
ç
÷
÷
ç
ç
÷
÷
÷
e
||
è
ø
è
ø
g ø
g ÷
m
g
b
çè- g b
çè- g b
÷
ç
÷
ø
è e
ø
p*^ = p^
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
88
Interludio:massimo momento trasferito
Abbiamo detto che il massimo momento trasferito
alla particella 2 (elettrone) si ha quando essa
ritorna indietro
p|| = m e g *b *
æE e* ö
çç ÷
÷=
çç * ÷
÷
÷
çè pe || ø
÷
æ me g * ö
÷
çç
÷
÷
çç
* *÷
÷
÷
èç- m e g b ø
Questo nel sistema del centro di massa
Ritorniamo nel sistema di laboratorio
Nel sistema di laboratorio la particella 2 ha il momento che si ottiene con la
trasformazione inversa
æE e ö
çç ÷
÷=
÷
çè pe || ÷
ø
æ g*
çç
çç * *
çè g b
g *b * öæ
me g * ö
÷
÷
ç
÷
÷
çç
÷
÷=
÷
* ֍
* *÷
÷
g øè
÷çm e g b ø
÷
æm e g *2 (1 + b *2 )ö
÷
çç
÷
÷
çç
÷
*2 *
÷
çè 2m e g b
÷
ø
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
89
Interludio:massimo momento trasferito
Pertanto la massima variazione di momento nel sistema di laboratorio è
D p = p f - pi = 2me g *2b* - 0 = 2me g *2b*
Utilizzando i valori trovati per g* e b*
b* =
Otteniamo
D p = 2m e
pp
E p + me
*
g =
E p + me
m p2 + m e2 + 2m e E p
pp
E p + me
m p2 + m e2 + 2m e E p
æ
m e2 - m p2
ç
= çç1 + 2
m p + m e2 + 2m e E p
è
ö
÷
÷
pp
÷
÷
ø
Nel caso del protone che incide su un elettrone fermo (mp me) vediamo che la
variazione di momento può essere approssimata come
1
æ
ö
÷
D p » çç1 pp
÷
me E p ÷
çç
÷
1+ 2
÷
ççè
mp mp ÷
÷
ø
In particolare se gp = Ep/mp 1 tutto il momento può essere trasferito
all’elettrone
D p » pp
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
90
Interludio:massima energia trasferita
Analogamente la variazione di energia del bersaglio è
D E = m e g *2 (1 + b *2 ) - m e = m e ( g *2 - 1 + g *2 b *2 )
Dal momento che g* = (1-b*2)-1 si verifica facilmente che
g *2 - 1 = g *2b *2
Otteniamo pertanto il risultato
D E = 2me g *2b *2
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
91
Parametro d’impatto: limite inferiore
Ritorniamo al parametro d’impatto
possiamo stimare il limite minimo bmin come il parametro d’impatto che
corrisponde alla massima energia trasferibile appena calcolata
D E = 2me g *2b *2
é ze 2
D E1 = ê
êë2peo
ù2 1
ú
2 2
ú
û mev b
ponendo g* g, b* b e uguagliando
é ze 2
ê
êë2peo
in conclusione
bmin
ze 2
=
2peo
ù2
1
2 2
ú
=
2
m
g
b
e
2 2
ú
m
b
b
û e min
1
2m e gb 2
ze 2
1
>
2peo 2m e g
=
z
r
g e
e2
re =
4peo m ec 2
Vedremo che questa approssimazione (classica) risulta troppo grossolana
produce un valore di bmin troppo piccolo
non tiene conto della meccanica quantistica
Istituzioni di Fisica Nucleare e Subnucleare – Francesco Ragusa
92