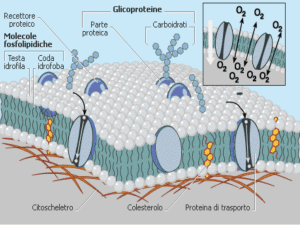
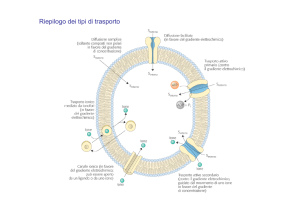
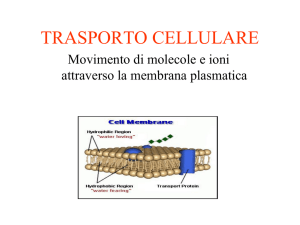
SCAMBI TRA CELLULA E AMBIENTE
Per comprendere i diversi modi con cui le
sostanze possono attraversare le membrane
cellulari è necessario prima capire come si
muovono le particelle di una sostanza (soluto)
che si trovi disciolta in acqua.
Definizione di flusso e di driving force
Il flusso (f) del soluto è la quantità
di esso che attraversa l’area
unitaria della superficie S
nell’unità di tempo.
Quantità moli, grammi
Superficie cm2, mm2
n
f 12= . .
N A t
Fs = f 1 2 - f 2 1
Flusso molare unidirezionale
Flusso netto o globale
n = numero di particelle; N = numero di Avogadro; A = superficie; t = tempo
La relazione generale che descrive l’intensità del flusso è
l’equazione di Teorell
Fi = ki · Xi
Essa prevede che l’intensità del flusso di soluto sia
proporzionale alla forza spingente che causa lo spostamento
delle sue particelle (Xi) a meno di una costante di
proporzionalità (ki) che dipende dalle caratteristiche delle
particelle di soluto ma anche da quelle del solvente e dalla
geometria in cui il flusso si determina.
Modalità di flusso in una soluzione acquosa
In una soluzione si possono avere tre modalità di flusso delle
particelle di soluto (molecole o ioni) o di solvente (1' acqua), che si
differenziano per la natura della “driving force” che determina lo
spostamento delle particelle:
1) il flusso di massa "bulk flow", in cui la "driving force" è generata
da una differenza di pressione idraulica tra regioni diverse della
soluzione;
2) la diffusione, in cui la "driving force" è generata da una differenza
di concentrazione di particelle in zone diverse della soluzione;
3) la migrazione in campo elettrico di particelle elettricamente
cariche (ioni), in cui la "driving force" è generata da una differenza di
potenziale elettrico tra regioni diverse della soluzione.
Il flusso di massa
Quando tra due regioni di una
soluzione acquosa esiste una
differenza di pressione idraulica,
tutte le particelle, sia del soluto che
dell'acqua, verranno spinte a
muoversi consensualmente (in
massa) dalla regione a pressione
maggiore a quella a pressione
minore
In questo caso la "driving force" è
generata dalla differenza di pressione
P = (P1-P2) dovuta al dislivello nei
recipienti.
L'intensità del flusso massivo (Fm)
nel condotto sarà:
Fm = km (P1-P2)
perciò sarà tanto maggiore quanto maggiore è la differenza di pressione, a meno di
una costante di proporzionalità (km) che dipende unicamente dalla viscosità della
soluzione e dalla geometria (sezione e lunghezza) del condotto.
La diffusione nelle soluzioni
Si consideri un piccolo volume
all'interno di una soluzione; il numero
di particelle di soluto che, nel loro
moto casuale, usciranno ed entreranno
nell'unità di tempo da ogni lato del
volumetto sarà proporzionale al loro
numero, cioè alla concentrazione del
soluto al suo interno e all’esterno.
L'intensità di un flusso diffusionale (Fd) tra due regioni (a e b) della soluzione
sarà proporzionale alla differenza di concentrazione (Ca - Cb) del soluto, a meno di
una costante (kd) nota come coefficiente di diffusione libera del soluto, il cui valore
dipende fondamentalmente dalla "mobilità" delle sue particelle nella soluzione.
Quindi:
Fd = kd (Ca - Cb)
Questa equazione è nota come prima legge di Fick.
Kd = RT/Nf
(1)
R = costante universale dei gas
T = temperatura assoluta
N = numero di Avogadro
f = coefficiente di attrito
Se la particella che diffonde è sferica, il coefficiente di attrito è
espresso dalla legge di Stokes : f = 6r
(2)
Dove è la viscosità (cioè l’attrito interno al mezzo) ed r il raggio
della molecola che diffonde. Inserendo l’equazione 2 in 1 avremo
Kd =RT/N6r
si vede chiaramente che il coefficiente di diffusione è proporzionale
alla temperatura, quindi inversamente proporzionale alla viscosità
del mezzo e alle dimensioni della particella.
Qual è la legge temporale con cui, partendo da una condizione iniziale di ineguale
concentrazione di un soluto in regioni diverse di una soluzione, la diffusione porta alla
condizione finale di omogenea concentrazione?
Iniziando dal tempo zero fino all'equilibrio finale, la velocità con cui aumenta la
concentrazione del soluto nel compartimento 2 verso il quale avviene il flusso diffusionale netto
di soluto (dC2/dt) sarà proporzionale, in ogni intervallo di tempo, al flusso netto diffusionale F (il
fattore di proporzionalità dipende dal volume del compartimento):
dC2/dt proporzionale ad F = f 1->2 – f 2->l = kd (C1-C2)
Risolvendo con il calcolo differenziale questa equazione in funzione del tempo, risulterà, come
indica il grafico seguente
La concentrazione del soluto in 2 cresce nel tempo secondo una funzione
esponenziale, cioè dapprima rapidamente, poi sempre più lentamente man mano che
ci si avvicina alla condizione finale di equilibrio.
La seconda legge di Fick
La seconda legge di Fick stabilisce che il tempo impiegato da una
particella per diffondere cresce col quadrato della distanza.
Ne deriva che la diffusione è un fenomeno lento su scala macroscopica. Ciò è
coerente con il fatto che le frequenti collisioni rendono molto bassa la velocità
media delle molecole in una sola direzione.
Su scala microscopica, invece, un equilibrio diffusionale può essere raggiunto in
tempi molto brevi (dell'ordine dei msec) date le piccole distanze che le particelle
devono percorrere. Ciò è di importanza vitale per le cellule: infatti la diffusione è
uno dei processi fondamentali che consentono a molte sostanze che entrano nel
metabolismo cellulare (ad esempio i gas respiratori, ma anche ioni, molecole
inorganiche ed organiche nutritizie o di scarto) di passare rapidamente dall'uno
all’altro lato della membrana cellulare.
La migrazione in un campo elettrico
Si immagini di applicare una
differenza di potenziale (Va - Vc)
tra due elettrodi metallici (a =
anodo e c = catodo) immersi in una
soluzione acquosa di un elettrolita
(ad esempio KCl). La differenza di
potenziale crea nella soluzione un
campo elettrico che agisce sugli
ioni in cui si dissocia l'elettrolita
(nell' esempio K+ e Cl-),
determinando la migrazione di
quelli caricati positivamente
(cationi) verso il catodo e di quelli
caricati negativamente (anioni)
verso l'anodo.
Per ogni specie ionica presente nella soluzione, il flusso (Fc) delle particelle cariche che
attraversa nell'unità di tempo una sezione ideale (S) immaginata nella soluzione, sarà
proporzionale al gradiente di potenziale che si stabilisce attraverso la sezione per effetto della
differenza di potenziale (Va – Vc) esistente tra gli elettrodi a meno di una costante (zke) che
dipende dalla temperatura, dal numero e dalle caratteristiche degli ioni .
Fe = zke (Va – Vc)
Questa relazione non è che una formulazione della legge di Ohm
riferita ad una soluzione di elettroliti;
zke indica la conduttività della soluzione, parametro equivalente
alla conduttanza (g = 1/R) dei conduttori metallici.
Legge di Ohm: I = V/R oppure I = gV
L’elettrodiffusione
In genere sui soluti dei liquidi biologici, che sono in larga parte sali
organici dissociati i ioni , agiscono sia un gradiente di
concentrazione che un gradiente elettrico (si parla quindi di
elettrodiffusione).
L’elettrodiffusione viene descritta dall’equazione di Nernst-Planck
Fed = kd (C1-C2) + zke (V1-V2)
Dove (C1-C2) e (V1-V2) sono le differenze di concentrazione e di
potenziale che insieme generano il gradiente elettrochimico che
muove le particelle cariche.
PERMEABILITÀ DELLA MEMBRANA CELLULARE
Le leggi che governano i flussi diffusionali nelle soluzioni non
possono essere applicate alla diffusione transmembranale.
Poiché la membrana è un mezzo di natura diversa dalle soluzioni
acquose che si trovano ai suoi lati , il passaggio di soluti non
dipenderà dalla mobilità che essi hanno nelle soluzioni ma dalla
capacità che essi hanno di entrare e attraversare la membrana.
Il passaggio di una sostanza attraverso la membrana cellulare
dipende soprattutto dalla permeabilità che la membrana presenta nei
suoi confronti.
Coefficiente di permeabilità
Consideriamo il caso più semplice del passaggio di sostanze
disciolte nei liquidi intra- ed extracellulare che attraversino la
membrana plasmatica spinte solo da un gradiente di
concentrazione.
In queste condizioni il passaggio attraverso la membrana di una
generica sostanza (i) può essere descritto dalla semplice equazione
di Fick, valida per la diffusione libera nelle soluzioni, purché al
posto del coefficiente di diffusione libera (kd) si sostituisca una
nuova costante: il coefficiente di permeabilità (Pi). Questo
coefficiente è comprensivo di tutti i fattori che condizionano il
passaggio transmembranale della sostanza, quindi non solo delle
caratteristiche delle particelle, della temperatura, ecc., ma anche
dello spessore e della costituzione della membrana.
Immaginando allora che sostanza (i) si trovi, in corrispondenza
delle due superfici membranali, alle diverse concentrazioni Cl e C2,
il flusso transmembranale (Fi) sarà:
Fi= Pi (C1 - C2)
Il coefficiente di permeabilità (P) di una membrana per una
sostanza è di solito espresso come rapporto (kdm/x) tra il
coefficiente di diffusione della sostanza nel materiale costitutivo
della membrana (kdm) e lo spessore della membrana (x); esso
esprime la probabilità che le particelle hanno di passare dall'una all'
altra superficie della membrana per una data differenza di
concentrazione.
Il valore di P della membrana cellulare per le diverse sostanze è
molto variabile; per le sostanze idrosolubili, esso è inferiore al
coefficiente di diffusione che esse presentano nell' acqua.
Quindi la velocità con cui una sostanza può attraversare la membrana cellulare cresce col
crescere del coefficiente di permeabilità della membrana per essa. L’ingresso di una molecola
sarà tanto più rapido quanto maggiore è il coefficiente di permeabilità della membrana, ed
altrettanto rapido sarà l'aumento della sua concentrazione, quindi la sua disponibilità,
all'interno della cellula.
Molecole liposolubili
Molecole polari
in assenza di
trasportatore
Ioni e molecole polari
di piccole dimensioni
Molecole polari di
tutte le dimensioni
trasportatore
canale