Tema 1: Misura della probabilità di eventi
Esempio: Sistema di trasmissione dati
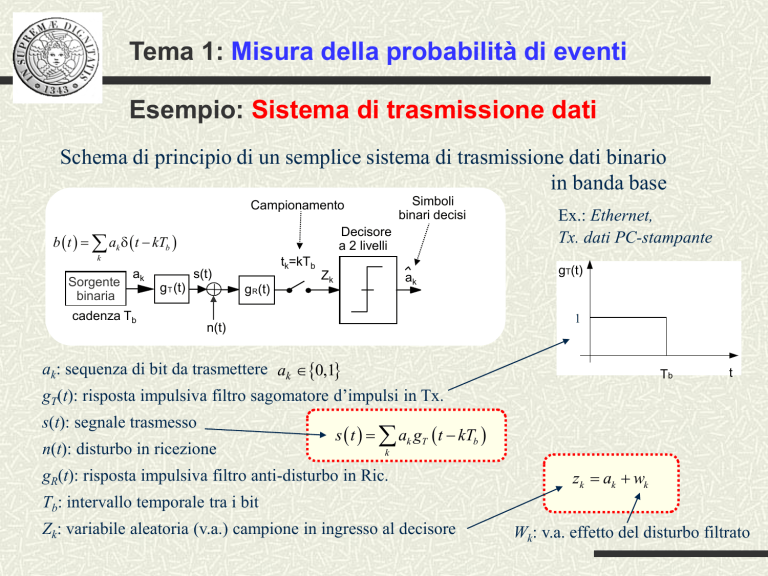
Schema di principio di un semplice sistema di trasmissione dati binario
in banda base
Simboli
binari decisi
Campionamento
Decisore
a 2 livelli
b t ak t kTb
k
Sorgente
binaria
ak
tk=kTb
s(t)
g T (t)
cadenza Tb
g R (t)
Zk
ak
Ex.: Ethernet,
Tx. dati PC-stampante
gT(t)
A1
n(t)
ak: sequenza di bit da trasmettere ak 0,1
Tb
t
gT(t): risposta impulsiva filtro sagomatore d’impulsi in Tx.
s(t): segnale trasmesso
n(t): disturbo in ricezione
s t ak gT t kTb
k
gR(t): risposta impulsiva filtro anti-disturbo in Ric.
zk ak wk
Tb: intervallo temporale tra i bit
Zk: variabile aleatoria (v.a.) campione in ingresso al decisore
Wk: v.a. effetto del disturbo filtrato
Variabili Aleatorie Binarie & Binomiali
Pr Ak 1 p , Pr Ak 0 1 p E Ai p, var Ai p(1 p)
n num. simboli binari trasmessi
K num. volte che si trasmette ak 1
n
K B( p, n) pk Pr K k p k (1 p) n k ; 0 k n, 0 p 1
k
Teorema di Bernoulli (o Legge dei grandi numeri):
K
F
n
1 n
lim F lim Ai lim Ai
n
n
n n
i 1
E F
E K
var F
n
var K
n
2
E Ai p Pr Ai 1
p
p (1 p )
n
ovvero, la frequenza di presentazione F tende
alla probabilità p che l’evento si verifichi
Statistiche della sorgente binaria
2
E
(
F
p
)
Fp
1 p
2
Errore relativo: =
E
p
p2
np
E 2 0.01
1 p
0.01
np
se p 1:
n
100
p
- Generare una sequenza di n=105 bit {ak} equiprobabili (p=0.5)
Sugg.: si utilizzi una trasformazione di v.a. del tipo funzione a gradino,
applicandola ad una v.a. uniforme su [0,1]
[istruzioni utili: rand, round, save]
- Verificare che i bit trasmessi sono equiprobabili (ovvero misurare p)
Sugg.: interpretazione della probabilità come frequenza relativa ...
[istruzioni utili: load, mean]
- Ripetere la verifica utilizzando solo i primi m bit e tracciare un grafico
della frequenza relativa di presentazione dell’evento {ak =1} in
funzione di m, con 1<m<n
Esempio di file.m & risultati
% Generatore sequenza bit trasmessi: genseq.m
% OUT: fileseqtx con la sequenza dei simboli binari ed equiprobab.
clear
clc
%bit trasmessi equiprobabili
ns=1e4 %lunghezza sequenza
seqtx=rand(1,ns);
% genera v.a. uniforme su [0,1]
seqtx=round(seqtx);
% trasf. di v.a. per ottenere la v.a.
% discreta valore del bit
save fileseqtx seqtx
Valutazione sperimentale di Pr{ak=1}:
con n=105 bit >>mean(seqtx)
= 0.4931
Ex.: con m=50 bit >>mean(seqtx(1:50)) = 0.5600
per un generico m<n >>mean(seqtx(1:m))
Valore effettivo: p=Pr{Ak=1}=0.5
Statistiche del segnale decodificato
V.A. campione in ricezione al decisore: Zk Ak Wk
con Wk v.a. Gaussiana a media nulla e varianza 2w
Regola del decisore:
1, se zk 0.5
aˆk
0, se zk 0.5
La probabilità di errore sui bit è, per il Teorema della Probabilità Totale,
Pe Pr e, Ak 1 Pr e, Ak 0 Pr e Ak 1 Pr Ak 1 Pr e Ak 0 Pr Ak 0
1
1
1
1
Pr e Ak 1 Pr e Ak 0 Pr Z k 0.5 Ak 1 Pr Z k 0.5 Ak 0
2
2
2
2
La soglia di decisione è equidistante rispetto ai valori ak 0, ak 1
La Gaussiana è una distribuzione simmetrica rispetto al val. medio
Uguali probabilità di errore per la decisione sui bit 1 e sui bit 0
0.5
0.5
Pe Pr e Ak 0 Pr Z k 0.5 Ak 0 =Q
1
w
w
Statistiche del segnale decodificato (2)
- Generare i campioni osservati Zk in ricezione, in ingresso al decisore,
a partire dalla sequenza di bit trasmessi, includendo il disturbo Gaussiano,
e ricavare i bit decodificati
Utilizzare i valori w 0.2149 e w 0.3902
[istruzioni utili: load, size, randn, sign]
- Valutare sperimentalmente la probabilità di errore (BER, bit error rate)
confrontando la sequenza trasmessa (n=105 bit) e quella ricevuta per i due
valori di w
[istruzioni utili: xor, mean]
- Confrontare il risultato sperimentale con quello teorico
[istruzioni utili: normcdf]
- Ripetere la valutazione sperimentale utilizzando solo i primi m=500 bit
Esempio di file.m & risultati
% Simulazione decisore e valutazione della BER: valber.m
function ber = valber(sigma)
% IN: deviaz. standard disturbo
load fileseqtx seqtx
% carica la sequenza bit trasmessi
zeta=seqtx+randn(1,size(seqtx,2))*sigma; % simula i campioni al decisore
seqri=(1+sign(zeta-1/2))/2;
% effettua le decisioni
seqer=xor(seqri,seqtx);
% calcola la sequenza degli errori
ber=mean(seqer)
% calcola la probabilità di errore
Valutazione sperimentale di Pe utilizzando n=105 bit:
con w 0.2149
= 0.0103
= 0.1019
con w 0.3902
(valore effettivo: BER=10-2)
Utilizzando solo m=500 bit:
(valore effettivo: BER=10-2)
= 0.0140
= 0.1160
(valore effettivo: BER=10-1)
(valore effettivo: BER=10-1)
Esempio di risultati: Misura della BER
Andamento teorico della BER:
0
10
-1
10
-2
Pe
10
SNR
PZ
(Signal-to-Noise Ratio)
2w
-3
10
0
10
Pe misurata
utilizzando
m=500 bit
-4
10
-1
10
-5
10
10
20
30
40
50
60
-2
70
10
Pˆe (500)
2
1/sigma
Pe
Pe
1 PZ
0.5
Pe Q
=Q
2 2
w
w
misurata
PPe emisurata
utilizzando
utilizzando
n=105 bit
n=10000
bit
Pˆe (105 )
Pe
-3
10
BER misurata:
-4
10
numero bit sbagliati nei primi m
Pˆe (m)
m
-5
10
10
20
30
40
1/sigma2
50
60
70
%
%
%
%
bersnr.m
Confronto tra valutazione e valore teorico della BER
al variare della deviazione standard del disturbo
generatore sequenza bit trasmessi
clear
clc
% bit trasmessi equiprobabili
ns=10000
% lunghezza sequenza
seqtx=rand(1,ns);
% genera v.a. uniforme su [0,1]
seqtx=round(seqtx);
% trasf. di v.a. per ottenere la v.a. discreta valore del bit
% simulazione decisore e valutazione probabilita' di errore sequenza bit ricevuti
sigma2i=[.001:5:80];
% valori di 1/sigma^2 del termine di disturbo (SNR=1/sigma^2)
sigma=sqrt(1./sigma2i); % valori di sigma
zeta=repmat(seqtx.',1,size(sigma,2))+randn(1,size(seqtx,2)).'*sigma; % simula i campioni al decisore
% per le varie deviazioni standard
seqri=(1+sign(zeta-1/2))/2;
% effettua le decisioni
% per le varie sequenze
seqer=xor(seqri,repmat(seqtx.',1,size(sigma,2)));
% calcola le sequenze degli errori
ber=mean(seqer);
% calcola le probabilità di errore
semilogy(sigma2i,ber,'-o')
grid
axis([min(sigma2i) max(sigma2i) 1e-5 1])
xlabel('SNR(db)')
ylabel('BER')
hold on
semilogy(sigma2i,1-normcdf(.5./sigma),'-xr')
% grafica le probabilità di errore
% grafica i valori teorici












