RIVELATORI AD LHC
Parte I
M. Cobal, Università di Udine
Caratteristiche rivelatori
Due problemi principali tipici di LHC
Pile up:
R = Ls = 109 interazioni / secondo
Protoni sono raggruppati in bunches (di 1011 protons)
collidenti nel punto di interazione ogni 25 ns
detector
Ad ogni interazione in media sono prodotti 40 eventi minimum-bias .
Questi si sovrappongono agli eventi interessanti (con high pT) , e causano il
cosiddetto
pile-up
~1000 particelle cariche prodotte per || < 2.5 ad ogni bunch crossing.
Comunque < pT > 500 MeV (particelle di minimum bias).
Taglio in pT permette di selezionare solo eventi interessanti
Soppressione del fondo:
Riconstruzione di oggetti con grande impulso trasverso
Come estrarre questo evento…
Higgs
4m
… da questo …
+30 min. bias events
2. danni da radiazione :
-- diminuiscono con la distanza d2 dal fascio i rivelatori vicino alla beam
pipe più inficiati
-- necessaria elettronica resistente alla radiazione
-- necessario il controllo di qualità di ogni pezzo di materiale
-- rivelatore + electtronica devono sopravvivee per almeno 10 anni
Requisiti dei rivelatori
Non sappiamo come la nuova fisica si manifesta rivelatori devono
essere flessibili e capaci di rivelare tutte le possibili particelle :
e, m, , , , jets, b-quarks, ….
esperimenti “ multi-purpose” .
•Impulso e carica delle tracce e dei vertici
secondari (esempio decadimenti dai quark b)
sono misurati nel tracker centrale. Richieste
eccellenti risoluzione in impulso e posizione
•Buona misura di leptoni con impulso trasverso da pochi GeV a pochi TeV : per la
rivelazione
-leptoni ad alto Pt (es. da decadimenti di W e Z)
-leptoni di basso Pt (es. nei decadimenti degli adroni B)
•Efficiente identificazione di elettroni (tracking e calorimetri), fotoni (calorimetri),
b/tau-jet (silicon strip e pixel detectors, calorimetri)
•Muoni identificati e impulso misurato in spettrometro a muon (+ tracker). Eccellente
risoluzione richiesta tra ~ 5 GeV < pT < ~ TeV
Energia e posizione di electroni e fotoni misurati nel calorimetro elettromagnetico.
Energia e posizione degli adroni e jets misurati principalmente nei calorimeteri
adronici. Buona copertura angolare e granularità .
Eccellente risoluzione in massa ( circa 1%) per particelle di massa fino a centinaia
di GeV che decadono in fotoni, elettroni e muoni
Requisiti dei rivelatori: rivelazione e misura dei neutrini
• I neutrini attraversano il rivelatore senza interagire
non possono quindi essere rivelati direttamente
Ma richiedendo
E f , Pf
=
E i , Pi
Energia totale, impulso
ricostruito nello stato finale
Energia totale , impulso
dello stato iniziale
Pi = 0
-- collisionatori
: Ei = s,
se un neutrino è prodotto allora Ef < Ei ( energia mancante)
P = - Pf
Pf 0
E = | P |
-- collisionatori adronici : energia e impulso dello stato iniziale non è noto
(energia e impulso dei partoni
che interagiscono ) .
e+e-
impulso trasverso iniziale e’
PT i = 0
e quindi impulso trasverso finale e’
PT f = 0
Ma se un neutrino è prodotto allora PT f 0( impulso trasverso mancante) e
miss
| PT |= | PT f | = E T
Requisiti dei rivelatori: ermeticita’
Usiamo il bilanciamento dell’energia-impulso nel piano trasverso
concetti quali Etmiss, impulso e massa trasversi sono più frequentemente usati
ricostruire “totalmente” alcune topologie con i neutrini,
es. W l e H ll h
il rivelatore deve quindi essere ermetico
energia trasversa misurata con alta accuratezza
nessun neutrino non-rivelato
Requisiti dei rivelatori: eccellente risoluzione in energia
Energia e posizione di elettroni e fotoni misurati nel calorimetro elettromagnetico
Esempio : H
H bassa risoluzione
H
alta risoluzione
background da
pp
s ( processi _ )
60
s ( H (100GeV ) )
m
Molti processi con grande sezione
d’urto e stessa topologia del segnale
nello stato finale.
Struttura non risonante e decrescente
con la massa invariante dei due fotoni
Larghezza del picco e’ dominata da
risoluzione energia e angolare del
calorimetro
Requisiti del rivelatore: eccellente capacità di identificazione
Esempio: separazione e/jet , /jet
jet
Il numero e il pT degli adroni in un jet hanno
grandi fluttuazioni
In alcuni casi nel jet c’e’un high-pT p0 e le altre
particelle troppo soffici per essere rivelate.
q
p0
q
Inner detector
e
EM calo
HAD calo
ATLAS
p0
Esempio p0 pt > 50 GeV d () < 1 cm a 150 cm (nel calorimetro! )
QCD jets possono simulare fotoni.
Rapporto fra rate di elettroni e di jet e’ e/jet= 10-5 per pt > 20 GeV. Quindi jet che
simulano elettroni devono essere rigettati di un fattore 106
s jj
s ( H )
~ 108
Mhiggs=100 GeV/c2 richiesta alta reiezione di jet.
Requisiti del rivelatore: eccellente capacità di identificazione
Esempio: i muoni
• Muon-ID da assorbimento e tracciamento nelle camere a muoni
• Carica dalla curvatura nel campo magnetico , Tracker e camere a Muoni
• Impulso trasverso pT: Tracker (~1%) e camere a Muoni (~10%) + Alignment
• Accettanza del tracker e delle camere a muoni
Tracciatura
Requisiti del rivelatore: misura dell’impulso trasverso
In un collisionatore adronico noi vogliamo misurare solo impulso trasverso
perche’ i processi avvengono tra partoni che non sono a riposo nel
sistema del laboratorio (conservazione dell’impulso solo nel piano
trasverso).
Coordinate
destrorse
r
f
Misura dell’impulso trasverso
Misura della deflessione
Ma in genere si usa la misura della
sagitta!
Risoluzione nella misura del momento
Un metodo utilizzato per determinare l’impulso (per un magnete in aria)
è la misura della sagitta (s)
L
x
B
La sagitta s è connessa al raggio di
curvatura r ed all’angolo di deflessione
tramite :
s = 1 cos = 2 sin 2
4
2
s
y
Poiché per particelle relativistiche q << 1
2
q
qBL
2
qBL2
=
s=
=
8
8 p
8p
Se B è in [T] L in [m] e p in [GeV/c]
0.3BL2
s=
8p
Risoluzione nella misura del momento
Per determinare la sagitta servono almeno 3 misure di posizione
una camera all’ingresso (x1), una al centro (x2) ed una all’uscita (x3) del magnete
s = x2
x1 x3
2
s(x) uguali per le 3 camere (vedi prossima slide) s( s) =
s( p)
s( s)
3/2× s( x )× 8 p
s( x ) × p
=
=
= 32.6
2
p
s
0.3BL
BL2
3
× s( x )
2
Se la traccia è misurata in N punti equispaziati lungo la lunghezza del magnete L, si può
dimostrare che la risoluzione in impulso dovuta all’errore della misura della traccia è:
y
L/
2
s p
S
B // z
R
q/
2
x
p/p = (720/N+4) xy p/(0.3BR2)
p
tr
=
s x
0.3BL2
720
p
N 4
Esempi:
Se ho 4 punti:
Per B=1.8 T, L=3 m, N=4 e s(x)=0.5 mm
s p
p
tr
10 3 p GeV / c
Contributo dello scattering multiplo
Risoluzione nella misura del momento
Sommando l’ errore dovuto all’incertezza della misura di posizione e il
MS.
s(p)/p %
30
s(p)/p|traccia
errore totale
20
s(p)/p|ms
10
100
200
300
p [Gev/c]
A seconda del range di momento che ci interessa possono adottare strategie differenti:
Per bassi momenti domina il termine costante
-minimizzare la lunghezza di radiazione
-usare camere leggere: X grande (per esempio camere con elio)
Per alti momenti bisogna
-aumentare il braccio di leva (BL2)
-aumentare la risoluzione sul punto (esempio rivelatori al silicio)
Solo sistema muonico
Solo tracker
Requisiti dei rivelatori: misure di precisione
Rivelatori di vertice
x=bc
IP=x/=bc
Il parametro di impatto e’
indipendente dal boost e
fornisce l’informazione sulla vita
media.
x
Il parametro di impatto (IP) e’ definito come
la minima distanza della traccia dal vertice
primario.
Vita media: parametro di impatto
•
Distanza tra la traccia carica estrapolata e il vertice primario
– 2D (piano trasverso, rφ)
– 2D + 1D (rφ + z, ATLAS)
– 3D (distanza euclidea, CMS)
vertice
secondario
(1)’
parametro
di impatto
(2)’
asse
del jet
vertice
primario
Jet da B
(2)
(1)
- Origine della traccia: punto di minor distanza tra la traccia e l’asse
del jet
a valle del vertice primario:
a monte del vertice primario:
IP positivo (1)
IP negativo (2)
25
Requisiti dei rivelatori di vertice
Raggio beam-pipe x angolo di MS dovuto
al material della beam-pipe
Risoluzione dei vertici in sistema solenoidale (CMS)
La posizione del vertice di interazione (primary vertex) per evento interessante lungo la
direzione z- dei fasci. ha uno spread di 8 cm (lunghezza del bunch). Quindi la posizione del
vertice non e’ nota con alta precisione per individuare la direzione delle particelle prodotte.
Sovrapposti eventi di pile-up con vertici spostati rispetto al PV.
Nel piano r-f le dimensioni del fascio
forniscono una coordinata precisa nella
posizione dei vertici
Al contrario in r-z la produzione di
multivertici richiede un rivelatore con alta
risoluzione nella coordinata z
Il sistema magnetico
ATLAS/CMS: differenze
Magnete principale e’ un toroide B= 0.7 T
Curvatura in (r,z)
Tracce dritte in (r, f)
estrapolazione
alla coordinata z del fascio (precisione al
cm).
Nel tracker c’e’ un solenoide B=2 T,
con curvatura in (r, f) .
I sistema a muoni non e’ nel ferro
Campo magnetico omogeneo
Solo un magnete. Solenoide B=4 T
Curvatura nel piano trasverso (r, f)
Tracce dritte in (r,z)
estrapolazione
fino al fascio
trigger sul parametro
di impatto
Giogo di ritorno del campo magnetico
nella camere a muoni
Campo magnetico non omogeneo a
largo
ATLAS/CMS: differenze
La scelta di CMS
Il magnete
Solenoide superconduttore che fornisce un campo intenso nel tracker e un flusso di
ritorno intenso per la misura dell’impulso dei muoni.
La scelta di ATLAS
-solenoide superconduttore integrato nel criostato del barrel ECAL che fornisce un
campo di 2T.
-Toroide nel Barrel: 8 bobine superconduttrici piatte, lunghe 25 metres e larghe 5
metri, raggruppate in forma di toroide.
-Due toroidi nell’Endcap: posizionati all’estremita’ del Solenoide, forniscono un
campo magnetico su una lunghezza radiale fra 1.5 e 5 metri.
ATLAS/CMS: vantaggi e
svantaggi: il magnete
ATLAS VANTAGGI: misura dei muoni con alta accuratezza in stand
alone (cioe’ in maniera autonoma – no tracker )( | | 2.7)
ATLAS SVANTAGGI: campo non uniforme nel volume del tracker
ATLAS SVANTAGGI: la posizione del solenoide in fronte a ECAL
barrel limita la risoluzione in energia in quella regione 1.2 | | 1.5
CMS VANTAGGI: intenso e uniforme campo magnetico fornisce una
eccellente risoluzione in impulso e una maggiore uniformita’ di prestazioni
su una copertura maggiore in eta
CMS SVANTAGGI: la posizione del solenoide fuori dal calorimetro limita
il numero di lunghezze di interazioni per l’assorbimento dello sciame
adronico.
CMS SVANTAGGI: il sistema muonico ha una capacita’ limitata di misura
di impulso stand-alone | | 1Importante il tracker.
“Compact” Muon Solenoid (CMS)
4T solenoid
Silicon Tracker
(200 m2)
PbWO4 Crystals
/ e detection
Hadronic calorimeter
Jets, missing ET ()
Muon chambers
CMS: Assemblaggio
Muon
chambers
solenoid
March 2007
Hadronic
calorimeter
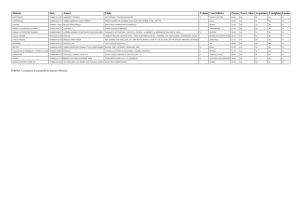
ATLAS
Diameter
Barrel toroid length
End-cap end-wall chamber span
Overall weight
25 m
26 m
46 m
7000 Tons
ATLAS Installazione
Sistema tracciante
Tracking a LHC
Pile-up e occupancy
L’impulso trasverso delle particelle di pile-up e’ circa 0.5-0.7 GeV.
Molte di esse sono ancora nel volume del detector mentre un secondo bx arriva.
Avremo le particelle di interesse (con alto impulso trasverso) + eventi di pile-up.
Il sistema di tracciamento deve essere in grado di rivelare tutte le tracce nell’evento. Le
tracce di pile-up ricostruite vengono poi scartate in quanto non provengono dallo stesso
punto di interazione (I vertici sono separati di circa 1 cm su circa 8 cm lungo la direzione
del fascio.
La complessita’ di ricostruzione delle tracce e’ legata all’occupancy : numero medio di
hits per evento in un elemento del detector. In caso di bassa occupancy la probabilita’
che 2 tracce si sovrappongano nello stesso elemento e’ bassa. L’occupancy deve
rimanere < 1% per avere un attima efficienza di ricostruzione.
La densita’ di tracce attese per bx a distanza r e a =0 e’ (40 x 1/r2).
Occupancy a 1% -> elemento di detector 0.00025 x r2
-> superficie di una strip di silicio di 10 cm con
pitch=100mm a 20 cm dalla beam pipe.
Resistenza a radiazione
Risposta veloce in modo da minimizzare il pile-up
Tracking a LHC
tracker interno (pixel) + central detector (silicio+TRT(Atlas) + muon system
Sistema di muoni meno inficiato dalla problematiche suddette (r> 4m)
Requisiti del tracker a LHC
• Efficiente & robusto algoritmo di tracking
– Granularita’ fine per risolvere tracce vicine
– Tempi rapidi di risposta per distinguere fra bx
• Abilita’ di ricostruire oggetti pesanti
– 1~2% pt resolution at ~ 100 GeV
• Capacita’ di operare in un ambiente pieno di tracce
– Nch/(cm2*25ns) = 1.0 a 10 cm
• Capacita’ di b/ tagging attraverso I vertici secondari
– Buona risoluzione nel parametro di impatto.
• Efficienza di ricostruzione
– 95% per tracce adroniche isolate con alto pt
– 90% per tracce di alto pt dentro i jets
• Capacita’ di operare in condizione di grande
irraggiamento.
– Silicon detectors opereranno a -7°C -10°C to contain reverse
annealing e limitare I danni da irraggiamento
Due stategie diverse: Atlas
2.3 m x 5.3 m Solenoid ~ 2 Tesla Field
~ 4 Tesla Toroid Field
ATLAS
ATLAS Inner Detector
Dentro il solenoide 2T
Tracking di precisione:
• Pixel detector (2-3 punti)
• Semiconductor Tracker –
SCT (4 punti)
Continuous Tracking:
(per pattern recognition
& id
elettroni)
• Transition Radiation Tracker –
46m) Long, 22m Diameter, 7’000 Ton Detector
TRT (36 punti
ATLAS Inner Tracker
ATLAS Pixel Detector
• 3 piani nel barrel
– r = 5.05 cm (B-layer), 9.85 cm, 12.25 cm
• 3 coppie di dischi Forward/Backward
– r= 49.5 cm, 6.0 cm, 65.0 cm
– ~ 2% di tracce con meno di 3 hits
• Dimensioni del pixel:
– 50 mm x 300 mm (B layer) & 50 mm x 400 mm
(direzione z piu’ precisa!)
• ~ 2.0 m2 di area sensibile con 8 x 107 canali
• Moduli sono gli elementi costitutivi di base
– 1456 nel barrel + 288 nell’ endcaps
– Area attiva 16.4 mm x 60.8 mm
– Area sensibile letta da 16 FE chips ciascuno
con una matrice di pixel18 columns x 160 row
1.04 m
ATLAS SCT Detector
Barrel: 4 piani
• pitch ~ 80 mm
• raggi: 284 – 335 – 427 – 498 mm
• 2112 moduli, con due detector per lato,
Tutti I rivelatori sono doppia faccia
(40 mrad angolo stereo )
• 4088 moduli
• 61 m2 di silicon
• 6.3 x 106 canali
Endcap: 9 coppie di ruote
• pitch 70 - 80 mm
• 3 tipi di moduli
Inner (400)
Middle (640 )
Outer (936)
ATLAS Transition Radiation Tracker (TRT)
Fornisce 35 punti con risoluzione circa 170mm
Barrel
Straw diameter - 4 mm
Wire diameter - 30 μm
End-caps
Polypropylene foil/fibre
radiators
Length:
Total
Barrel
End-cap
Outer diameter
Inner diameter
6802 cm
# straws: Total
148 cm
Barrel
257 cm
End-cap
206 cm
# electronic channels
96-128 cm Weight
372 832
52 544
319 488
424 576
~1500 kg
Gas 70%Xe+27%CO2+3%O2
• Xe for good TR absorption
• CO2 > 6% for maximum
operation stability
Gas gain 2.5104
43
Tubi straw e assorbitore
Stessa tecnologia per il barrel e per
l’endcap
~25 mm
~5 mm
~0.2 mm
~6 mm
~70 μm
Straw wall
Filo anodico tungsteno
con coating di oro
Per rendere la straw rigida vengono
attaccate 4 C-fibre
Radiazione di transizione e’ prodotta
quando una particella ultra-relativistica
attraversa l’interfaccia fra due mezzi
differenti (fibre o fogli & aria per TRT).
Fotoni TR sono emessi a piccoli angoli
rispetto alla traettoria della particella
incidente
Deposito di energia nei TRT e’ la somma
della perdita per ionizzazione delle
particelle cariche (~2 keV) e grandi
depositi dovuti a fotoni assorbiti (> 5 keV)
Transition Radiation
~1 TR hit
Bod -> J/yKos
~7 TR hits
Electrons with
radiator
High threshold hits
Electrons without radiator
Particelle cariche con alto-γ (e.g. elettroni)
emettono radiazione di transizione (X-rays)
quando attraversano il radiatore. Questa
radiazione viene rivelata nei tubi straw (8-10
KeV)
Due soglie per separare le particelle
TR threshold – electron/pion separation
5.5 keV
MIP threshold – precise tracking/determinazione tempo di drift time 2 keV
Sistema di tracciamento: ATLAS e CMS
Prestazioni del tracker di CMS
superiori rispetto ad ATLAS in
termini di risoluzione in impulso
(campo piu’ uniforme e intenso e misura piu’
accurata a grande raggio )
Vertexing and b-tagging
prestazioni sono simili
2
ATLAS
X/X0
1.5
Impatto sulle prestazioni
(degrado efficienza e
risoluzione – scattering
multiplo) dalla quantita’ di
materiale e’ importante
sia in CMS che ATLAS)
1
CMS
0.5
0
-4
-2
0
2
4