Fattorizzazione per differenza dei fattori

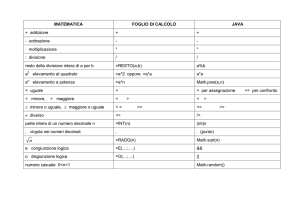
Fattorizzare i numeri interi
Ci sono molti algoritmi efficienti per fattorizzare numeri interi e molti sono i testi dove è possibile trovare una
completa trattazione sull'argomento, Qui vogliamo proporre dei sistemi (in parte abbastanza originali e forse
relativamente veloci ma senza nessuna pretesa da parte nostra) per cercare di trovare i fattori di un numero
intero con metodi algebrici e facilmente implementabili in un moderno calcolatore. L'idea è comunque quella
di trovare dei limiti entro cui cercare con maggiori probabilità le soluzioni. Nella ricerca delle soluzioni
prendiamo principalmente in esame solo valori interi positivi benché in linea di principio potremmo
considerare anche i negativi dal momento che 9 = 3*3 = (-3)*(-3). Facendo girare tutti gli algoritmi in
parallelo aumenta la probabilità di trovare soluzioni in tempi rapidi. Ogni algoritmo sarà implementato con
una applicazione scritta in C/C++ o in PARI/Gp per la gestione dei grandi numeri
Considerazione preliminare (algoritmo 0)
Dato un numero p da fattorizzare di n cifre è facile provare che almeno un fattore deve essere dell'ordine di
W  10
n
int  1
2
cioè deve avere almeno int(n/2) cifre con int(x) la parte la funzione parte intera di x.
Se p = ab con a, b numeri primi allora entrambi i fattori sono entrambi maggiori di W cioè tali per cui
a > W, b > W cioè S= a+b >2 W. In questo particolare caso possiamo porre anche
W  10
n
int 
2
1
Considerare W ci è particolarmente utile quando trattiamo di grandi dimensioni perché come vedremo meglio
con gli altri algoritmi ci può aiutare a trovare dei limiti per i fattori da ricercare.
LISTATO IN C++
#include <stdio.h>
#include <math.h>
#include <iostream.h>
int main(int argc, char *argv[])
{
long double x, p;
long i = 0;
int cifre;
cout << "inserisci il numero di cifre del numero intero";
cin >> cifre;
cout <<" inserisci il numero da fattorizzare";
cin >> p;
x = pow(10, int(cifre/2)-1 );
do{
x = x + 1;
i = i + 1;
} while(int(p/x) != (p/x));
cout << "un fattore e' " << x;
cout <<" passi di elaborazione: " << i;
cin >> "---------";
return 0;
}
2
LISTATO IN PARI/GP
{ algo2(cifre) = local(x, p);
p = nextprime(10^10)*nextprime(10^12);
x = 10^(floor(cifre/2)-1);
while(floor(p/x) != (p/x), x=x+1);
print(x);
print("-----");
print(p/x);
return (1);}
Primo algoritmo (AL-1) (variante della fattorizzazione alla Fermat)
p  x1 x2 (in generale non è detto che ci siano solo due fattori come nell'RSA ma il procedimento di
fattorizzazione può essere ripetuto per ognuno dei due fattori trovati finché non si arriva a fattori che hanno
decomposizione banale cioè che sono primi).
x1 
p , x1 
x2 
p
p
2
x1, 2  0
x1ORx 2  W dove OR sta ad indicare che la relazione vale per una radice o per entrambe
tutti i numeri interi positivi (ove la ricerca può essere fatta in modo sequenziale oppure
random)
Attenzione: per P molto grande A(p) cioè il numero dei primi minori di P è approssimativamente
p/log(p)
3
LISTATI IN C++ E IN VISUAL BASIC .NET
Nei codici sorgenti in C++ che seguono ho usato l'espressione 'int(p/x)' per semplicità tuttavia
sarebbe meglio sostituirla con la più esatta sintatticamente floor(fabs(p/x)).
#include <stdio.h>
#include <iostream.h>
#include <math.h>
int main(int argc, char *argv[])
{
long double x, p;
long i, j;
j = 0;
cout << "inserisci il numero da fattorizzare ";
cin >> p;
for( i = int(sqrt(p)); i <= int(p/2); i++)
{
j = j +1;
if(int(p/i) == (p/i))
{
cout << "fattore: " << i << "\n";
cout << "passi: " << j << "\n";
}
}
cin >> "-----------------"
}
return 0;
lo stesso algoritmo può essere implementato in Visual Basic .Net usando per la ricerca dei fattori
un generatore di numeri casuali: la ricerca si rileva molto più veloce:
Module Module1
Sub Main()
Dim p As Decimal
Dim generator As New Random
Dim a As Decimal
Dim i As Integer
i=0
Console.WriteLine("inserisci il numero da fattorizzare")
p = Console.ReadLine()
Do
a = generator.Next(2, Int(Math.Sqrt(p)))
4
i=i+1
Loop While ((p / a) <> Int(p / a))
Console.Write("fattore: ")
Console.Write(a)
Console.Write("passi: ")
Console.Write(i)
Console.ReadLine()
End Sub
End Module
LISTATI IN PARI/GP
{fermat(p) = local(x);
x = floor(sqrt(p));
while (floor(p/x) != (p/x), x--);
print(x);
print("----");
print(p/x);
return (1);}
{fermat2(p) = local(a, x, y);
a = floor(sqrt(p));
x = random(a);
y = precprime(x);
while (floor(p/y) != (p/y), x = random(a);y = precprime(x));
print(y);
print("----");
print(p/y);
return (1);}
{fermat3(p) = local(a, x, y);
a = floor(sqrt(p));
x = random(a);
while (floor(p/x) != (p/x), x = random(a));
print(x);
print("----");
print(p/x);
return (1);}
5
{fattore2(p) =local(s, x);
s = truncate(sqrt(p));
x = precprime(s);
while (truncate(p/x) != (p/x),
s--;
x = precprime(s));
print(x);
return (1);}
{fattore3(p)= local(s, x);
s=0;
x = nextprime(s);
while (truncate(p/x) != (p/x),
s++;
x = nextprime(s));
print(x);
return (1);}
{fattore4(p)= local(s, x);
s=truncate(p/2);
x = precprime(s);
while (truncate(p/x) != (p/x),
s--;
x = precprime(s));
print(x);
return (1);}
{fattore5(p)= local(s, x);
s=truncate(p/2);
x = nextprime(s);
while (truncate(p/x) != (p/x),
s++;
x = nextprime(s));
print(x);
return (1);}
6
Secondo algoritmo (Al-2)
Dalla nota relazione
x 2  sx  p  0
s  x1  x2
p  x1 x2
x1, 2
s  s2  4 p

2
s  2 p , s  2 p
Supponiamo di stare a considerare un tipico problema RSA quindi p ha solo due fattori ed s è sicuramente
un numero pari essendo la somma di due primi quindi di due numeri dispari. Cerchiamo di velocizzare la
ricerca dei fattori usando l’elemento W precedentemente descritto.
x1 
s  s2  4 p
 W mi porta a dover risolvere il seguente sistema:
2
s  2 p oppure
s
s  2 p
W2  p
W
s  s2  4 p
x2 
 W mi porta a dover risolvere il seguente sistema:
2
7
2W  s  0
s2  4 p  0
s2  4 p  0
unito alle soluzioni del sistema 2W  s  0
s
W2  p
W
Osservazione
x y
1) s  4 p  0 equivale alla ben nota relazione 
  xy
 2 
2
2
2) se d 
s
2
allora x1, 2  d  d  p (più avanti approfondiremo questo caso)
2
int( )
xy
px
x 2 k  pk  px
, xy  p porta a
3) x  y 
dove pi può supporre k  10 2
 0 ovvero k  2
k
xk
x p
n
con n il numero delle cifre di P. Trovare k  int(
px
) ci aiuta a calcolare una stima superiore per s =
x p
2
x+y per aumentare anche grazie al punto 1) la ricerca delle soluzioni.
LISTATO IN C++
#include <stdio.h>
#include <math.h>
#include <iostream.h>
int main(int argc, char *argv[])
{
long double p, x, y, s;
long i;
cout << "inserisci il numero da fattorizzare ";
cin >> p;
s = 2* int(sqrt(p));
i = 0;
do {
x = (s + sqrt(pow(s,2)-4*p))/2;
8
y = (s - sqrt(pow(s,2)-4*p))/2;
s = s+1;
i = i+1;
}while((int(p/x) != (p/x)) || (int(p/y) != (p/y))) ; // si può mettere && (and) al posto di || (OR) ma una
delle due
cout << "un fattore e' " << x << "\n";
//soluzioni trovate potrebbe non essere intera
cout << "un fattore e' " << y << "\n";
cout << "passi: " << i;
cin >> "--------------------";
return 0;
}
LISTATI IN PARI/GP
{fatto(p) =local(s, x);
s = 2 * truncate(sqrt(p));
x = (s - sqrt(abs(s^2-4*p)))/2;
while (truncate(p/x) != (p/x), s++);
print(x);
return (1);}
{algo1(p) = local( s, d, x, y);
s = 2 * floor(sqrt(p));
d = sqrt(abs(s^2-4*p));
x = (s + d)/2;
y = (s - d)/2;
while (floor(p/x) != (p/x) && floor(p/y) != (p/y),
s++;
d = sqrt(abs(s^2-4*p));
x = (s + d)/2;
y = (s - d)/2);
print(x);
print("----");
print(y);
return (1);}
9
{algo1(p) = local(s, d, x, y);
s = floor(sqrt(p));
d = sqrt(abs(s^2-p));
x = (s + d);
y = (s - d);
while (floor(p/x) != (p/x) && floor(p/y) != (p/y),
s = s+1;
d = sqrt(abs(s^2-p));
x = (s + d);
y = (s - d));
print(x);
print("----");
print(y);
return (1);}
{algo2b(p) = local(b, d, x, y);
b = floor(sqrt(p));
d = sqrt(abs(b^2-p));
x = b + d;
y = b - d;
while (floor(p/x) != (p/x) && floor(p/y) != (p/y),
b++ ;
d = sqrt(abs(b^2-p));
x = b + d;
y = b - d);
print(x);
print("----");
print(y);
return (1);}
VARIANTE
s 2  4 p s 2  4 p  a, a  0, p  xy a numero pari perché differenza di due numeri pari
Ciò porta all’equazione biquaratica
x 4  x 2 (a  2 p)  p 2  0
x1, 2 
a  2 p  a 2  4ap
2
10
LISTATO IN C++
#include <stdio.h>
#include <math.h>
#include <iostream.h>
int main(int argc, char *argv[])
{
float a, x, y, p;
long double i;
cout << "inserisci il numero da fattorizzare ";
cin >> p;
a = 0;
i = 0;
do{
x = sqrt( (a+2*p+sqrt(pow(a,2)+4*a*p))/2);
y = sqrt( (a+2*p-sqrt(pow(a,2)+4*a*p))/2);
a = a+1;
i = i+1;
} while ((int(p/x) != (p/x)) || (int(p/y) != (p/y))) ; // si può mettere && (and) al posto di || (OR) ma una
cout << "fattore: " << x << "\n";
cout << "fattore: " << y << "\n";
cout << "passi: " <<i << "\n";
cin >> " -----";
return 0;
// delle due soluzioni trovate potrebbe non essere intera
}
LISTATO IN PARI/GP
{algo3(p) = local(a, x, y, d);
a = 0;
d = sqrt(abs(a^2+4*a*p));
x = sqrt(abs((a+2*p+d)/2));
y = sqrt(abs((a+2*p-d)/2));
while (floor(p/x) != (p/x) && floor(p/y) != (p/y),
a++;
d = sqrt(abs(a^2+4*a*p));
x = sqrt(abs((a+2*p+d)/2));
y = sqrt(abs((a+2*p-d)/2)));
print(x);
print("----");
print(y);
return (1);}
11
Terzo algoritmo (Al-3)
Dalle Osservazioni precedenti deduciamo che
2
2
 s  m
      p dove m è intero
2  2 
x2 
s m

2 2
x1 
s m

2 2
allora
x12  mx1  p  0 , x22  mx2  p  0
da cui si può partire direttamente da m per trovare le soluzioni
x1 
m  m2  4 p
 m  m2  4 p
x2 
2
2
con m   s  4 p ,
2
s  m, s  2 p
(possiamo considerare anche le soluzioni negative di X1, X2 quelle con il segno - ovvero
x1 
m  m2  4 p
2
x2 
 m  m2  4 p
ma il ragionamento sarebbe identico a quello già fatto)
2
12
Sempre nell’ipotesi di considerare un problema di fattorizzazione RSA usiamo il fattore W per accelerare la
ricerca delle soluzioni. Consideriamo per semplicità le soluzioni positive ma lo stesso discorso vale per quelle
negative
m  m2  4 p
 W porta a risolvere il seguente sistema
2
x
m2  4 p  0
unito alle soluzioni di
2W  m  0
x=
m  2W  0
W2  p
m
W
 m  m2  4 p
 W porta a dover risolvere il sistema
2
m2  4 p  0
2W  m  0
m
p W 2
W
m  2W
 m  m2  4 p
x
 W allora m 2  4 p  0
2
W2  p
m
W
13
LISTATO IN C++
#include <stdio.h>
#include <math.h>
#include <iostream.h>
int main(int argc, char *argv[])
{
long double m, x, y, p;
long i;
cout << "inserisci il numero da fattorizzare ";
cin >> p;
m = 0;
i = 0;
do{
x = (m + sqrt(pow(m, 2) + 4*p))/2;
y = (-m + sqrt(pow(m, 2) + 4*p))/2;
m = m+1;
i = i+1;
} while ( (int(p/x) != (p/x)) || (int(p/y) != (p/y))); // si può mettere && (and) al posto di || (OR) ma una
cout << "fattore: " << x << "\n";
cout << "fattore: " << y << "\n";
cout << "passi: " <<i << "\n";
cin >> " -----";
}
// delle due soluzioni trovate potrebbe non essere intera
return 0;
LISTATO IN PARI/GP
{algo4(p) = local(m, x, y);
m= 0;
d = sqrt(m^2+4*p);
x = (m+d)/2;
y = (-m+d)/2;
while (floor(p/x) != (p/x) && floor(p/y) != (p/y),
m++ ;
d = sqrt(m^2+4*p);
x = (m+d)/2;
y = (-m+d)/2);
print(x);
print("----");
print(y);
return (1);}
14
Quarto algoritmo (Al-4)
p  x1 x2  a 2  b 2  (a  b)(a  b)
x1  a  b, x2  a  b
x1  x2  2b
x1  x2  2a ciò porta a
x12  2bx1  p  0 , x12  2ax1  p  0
x1  a  a 2  p , x1  b  b 2  p (possiamo considerare anche la soluzione negativa quella con
segno - , però poi occorre calcolare il suo valore assoluto)
Come nei casi precedenti
x  a  a 2  p  W porta a:
a  p,a   p
a2  p  0
unito alle soluzioni di a  W  0
W a 0
W2  p
a
W
x  a  a 2  p  W porta al sistema di condizioni
a
p, a   p
a W
a
W2  p
W
15
x  b  b 2  p  W
allora
b2  p  0
b  p0
unito a W  b  0
W b  0
p W 2
b
2W
2
x  b  b 2  p  W ciò porta a:
b  W
b2  p  0
p W 2
b
2W
osservazione: se p  x1 x2 è un problema RSA allora x1  x2  2a x1  2a  x2 quindi
x22  2ax2  p  0 x 2  a  a 2  p con a 2  p
LISTATO IN C++
#include <stdio.h>
#include <math.h>
#include <iostream.h>
int main(int argc, char *argv[])
{
long double x, y, p;
long a;
long i = 0;
cout<< "inserisci il numero da fattorizzare ";
cin >> p;
a = int(sqrt(p));
a = a+1;
do {
x = a + sqrt(pow(a,2) -p);
y = a - sqrt(pow(a,2) - p);
a = a+1;
16
i = i+1;
} while( (int(p/x)!=(p/x)) ||(int(p/y) != p/y)) ; // si può mettere && (and) al posto di || (OR) ma una
delle due
cout << "fattore: " << x << "\n";
// soluzioni trovate potrebbe non essere intera
cout << "fattore: " << y << "\n";
cout << "passaggi: " << i;
cin >> "-------------"; return 0;}
LISTATO IN PARI/GP
{algo5(p) = local(a, d, x, y);
a = floor(sqrt(p));
d = sqrt(abs(a^2-p));
x = a+d;
y = a-d;
while (floor(p/x) != (p/x) && floor(p/y) != (p/y),
a = a+1 ;
d = sqrt(abs(a^2-p));
x = a+d;
y = a-d);
print(x);
print(y);
return (1);}
LISTATO IN C++
#include <stdio.h>
#include <math.h>
#include <iostream.h>
int main(int argc, char *argv[])
{
long double x, p;
long b;
long i = 0;
cout<< "inserisci il numero da fattorizzare ";
cin >> p;
b = int(sqrt(p));
b = b+1;
do {
x = - b + sqrt(pow(b,2) + p);
17
b = b+1;
i = i+1;
} while((int(p/x)!=(p/x)));
cout << "fattore: " << x << "\n";
cout << "fattore: " << y << "\n";
cout << "passaggi: " << i;
cin >> "-------------";
return 0; }
LISTATO IN PARI/GP
{algo6(p) = local(s, x);
b = floor(sqrt(p));
x = -b + sqrt(abs(b^2 +p));
while (floor(p/x) != (p/x),
b++;
x = (s + sqrt(abs(s^2-4*p)))/2);
print(x);
print("----");
print(p/x);
return (1);}
Quinto algoritmo (Al-5)
Se
p  x1 x2 , x2  x1  a allora sostituendo le variabili ottengo che
 a  a2  4 p
x  x1a  p  0 quindi x1 
2
2
1
Consideriamo la soluzione positiva come negli altri casi
x
 a  a2  4 p
 W allora dobbiamo risolvere
2
18
a  2W
a2  4 p  0
x
a  2W
unione a
a
p W 2
W
a  a2  4 p
W allora il sistema diventa:
2
2W  a  0
a2  4 p  0
a
W2  p
W
analogamente si arriva agli stessi risultati nel caso opposto cioè che x2
 x1  a abbiamo
a  a2  4 p
che x 
.
2
Quindi
a2  4 p  0
a  4p  0
unito a 2W  a  0
2W  a  0
W2  p
a
W
2
Come negli altri casi si sarebbe potuto considerare per X1 e X2 anche le soluzioni negative , quello con
segno - poi si sarebbe dovuto calcolare il loro valore assoluto
19
LISTATO IN C++
#include <stdio.h>
#include <math.h>
#include <iostream.h>
int main(int argc, char *argv[])
{
long double x, y, p;
long a;
long i = 0;
cout<< "inserisci il numero da fattorizzare ";
cin >> p;
a = 0;
a = a+1;
do {
x = (-a+sqrt(pow(a,2)+4*p))/2;
y = (a+sqrt(pow(a,2)+4*p))/2;
a = a+1;
i = i+1;
} while( (int(p/x)!=(p/x)) ||(int(p/y) != p/y)) ; // si può mettere && (and) al posto di || (OR) ma una delle
due
cout << "fattore: " << x << "\n";
// soluzioni trovate potrebbe non essere intera
cout << "fattore: " << y << "\n";
cout << "passaggi: " << i;
cin >> "-------------";
return 0;
}
LISTATO IN PARI/GP
{algo7(p) = local(a, d, x, y);
a = 0;
d = sqrt(a^2+4*p);
x = (-a + d)/2;
y = (a + d)/2;
while (floor(p/x) != (p/x) && floor(p/y) != (p/y),
a = a+1;
d = sqrt(a^2+4*p);
x = (-a + d)/2;
y = (a + d)/2);
print(x);
print("----");
print(y);
return (1);}
20
Sesto algoritmo (Al-6)
Partiamo da un ben nota relazione algebrica sempre vera:
x2  y2
 xy quindi x 2  y 2  2 xy  2a a > 0 y = p/x
2
arriviamo a
x 4  2 x 2 ( p  a)  p 2  0 quindi le soluzioni sono x1, 2 
p  a  a 2  2 pa dove però
per evitare errori di calcolo sostituiamo ad a a/2 per effetto della disuguaglianza di partenza
LISTATO C++
#include <stdio.h>
#include <math.h>
#include <iostream.h>
int main(int argc, char *argv[])
{
long double x, y, p;
long int i, a, c;
a = 0;
i = 0;
cout << "inserisci numero ";
cin >> p;
do{
x = sqrt(p+a+sqrt(pow(a,2)+2*p*a));
y = sqrt(p+a-sqrt(pow(a,2)+2*p*a));
a = a+1; // qui è meglio mettere a = a+ 1/2 se non è un problema RSA;
i = i +1;
}while( (int(p/y) != (p/y)) || (int(p/x) != (p/x)) ) ; // si può mettere && (and) al posto di || (OR) ma
cout << "fattore: " << x << "\n";
// una delle due soluzioni trovate potrebbe non essere intera
cout << "fattore: " << y << "\n";
cout << "passi: " << i;
}
21
LISTATO IN PARI/GP
{algo8(p) = local(a, d, x, y);
a = 0;
d = sqrt(a^2+2*p*a);
x = sqrt(abs(p+a+d));
y = sqrt(abs(p+a-d));
while (floor(p/x) != (p/x) && floor(p/y) != (p/y),
a = a+0.5;
d = sqrt(abs(a^2+2*p*a));
x = sqrt(abs(p+a+d));
y = sqrt(abs(p+a-d)));
print(x);
print("----");
print(y);
return (1);}
Fattorizzazione con le disequazioni
Nel campo della fattorizzazione dei numeri possono essere impiegate le disuguaglianze notevoli
(a  b) 2  a 2  b 2  2ab
ab 
a 2  b 2 ( a  b) 2

2
2
quindi
ab 
a2  b2
2
ora da
(a  b) 2  a 2  b 2  2ab
ab 
( a  b) 2 a 2  b 2

2
2
22
quindi
ab 
( a  b) 2
2
ma allora
m 2  ab 
a 2  b 2 ( a  b) 2

2
2
con m = min(a,b)
in modo del tutto analogo da
(a  b) 3  a 3  3a 2 b  3ab 2  b 3
procedendo come sopra ho che
ab 
( a  b) 2
3
delle altre disuguaglianze abbiamo già detto di quest'ultima no.
s 2  3 p, s 2  3 p  a, a  0
se y = P/x allora
x 4  x 2 ( p  a)  p 2  0
x
p  a   3 p 2  2 pa  a 2
2
con a > 0 a > p, (a < -3p per a < 0)
23
LISTATO IN C++
#include <cstdlib>
#include <iostream>
#include <math.h>
using namespace std;
int main(int argc, char *argv[])
{
double x, p, a, start;
cout << "inserisci il numero da fattorizzare ";
cin >> p;
a = p;
do
{
x = sqrt( (p+a+sqrt(-3*pow(p,2)+2*p*a + pow(a,2)) )/2);
a = a+1;
} while(int(p/x) != (p/x));
cout << "fattore " << x;
system("PAUSE");
return EXIT_SUCCESS;
}
LISTATO IN C++
{algo10(p) = local(a, d, x, y);
a = p;
d = sqrt(abs(-3*p^2 + 2*p*a+a^2));
x = sqrt(abs((p+a+d)/2));
y = sqrt(abs((p+a-d)/2));
while (floor(p/x) != (p/x) && floor(p/y) != (p/y),
a = a+1;
d = sqrt(abs(-3*p^2 + 2*p*a+a^2));
x = sqrt(abs((p+a+d)/2));
y = sqrt(abs((p+a-d)/2)));
print(x);
print("----"); print(y); return (1);}
24
Fattorizzazione con il teorema di Bezout
Il famoso teorema di Bezout ci può aiutare a trovare i fattori di un problema RSA. Sia p = ap dal teorema di
Bezout sappiamo che se d=MCD(a,b) esistono u, v interi tali che d = ua + bv. Ora dato che
d=MCD(a,b) = 1 abbiamo che 1= au + bv. Da queste considerazioni esplicitando a e sapendo che p = ab
troviamo:
b 2 v  b  up  0
b
1  1  4uvp
2v
ove uv = k < 0 mentre v può essere v > 0, v < 0. in pratica il programma prima trova i possibili valori di k
poi cerca i valori di v:
LISTATO C++
#include <stdio.h>
#include <iostream.h>
#include <stdio.h>
#include <math.h>
int main(int argc, char *argv[])
{
double x, y, p, k, v;
double a, b;
int j, i;
k = 0;
v = 0;
cout << "inserisci un numero da fattorizzare ";
cin >> p;
do
{
k = k-1;
i = i+1;
a = 1-sqrt(1-4*k*p);
b = 1+sqrt(1-4*k*p);
25
} while (((a) != int(a)) && ((b) != int(b))) ;
do
{
v = v-1;
i = i+1;
x = a/(2* v);
y = b/(2* v);
} while (((p/x) != int(p/x)) && ((p/y) != int(p/y)));
if ((p/x) == int(p/x))
{
cout << "fattore "<< x << "\n";
}
else if ((p/y) == int(p/y))
{
cout << "fattore "<< y << "\n";
}
cout << "passi " << i;
cin >> j;
return 0;
}
Fattorizzazione con i logaritmi
Sia n = ab. Per le note proprietà dei logaritmi sappiamo che Log(n) = Log(ab) = Log(a) + Log(b).
Supponiamo che Log(a) = Log(b) quindi Log(n) = 2Log(a), cioè Log(a) = Log(n)/2
a  10
Log ( n )
2
Questo ci induce a cercare i fattori come
x1  10
Log ( n )
2
, x2  10
Log ( n )
2
possiamo utilizzare il parametro a al posto del già citato W o della radice
quadrata di n negli algoritmi precedenti per avere un migliore intervallo dove cercare le soluzioni
26
LISTATO C++
#include <cstdlib>
#include <iostream>
#include <math.h>
using namespace std;
int main(int argc, char *argv[])
{
long double m, x, y, p;
long i;
cout << "inserisci il numero da fattorizzare ";
cin >> p;
x = int(pow(10, log10(p)/2))+1;
y = int(pow(10, log10(p)/2))+1;
do{
x = x-1;
y = y+1;
i = i+1;
} while ( (int(p/x) != (p/x)) && (int(p/y) != (p/y)) );
cout << "fattore: " << x << "\n";
cout << "fattore: " << y << "\n";
cout << "passi: " <<i << "\n";
system("PAUSE");
return EXIT_SUCCESS;
}
LISTATO PARI/GP
{algo9(p) = local(p, d, x, y);
d = log(p)/log(10);
x = floor(10^d);
y = floor(10^d);
while (floor(p/x) != (p/x) && floor(p/y) != (p/y),
y = y+1;
x =x-1);
print(x);
print("----");
print(y);
return (1);}
27
Fattorizzazione con il metodo della bisezione
Sia p = ab il numero da fattorizzare con a, b numeri primi (nel caso si voglia trattare un problema RSA).
supponiamo di considerare p', p'', p' =a'b', p'' = a''b''
p' < p < p'' con a' < a < a'', b' < b < b''
ove a', a'', b', b'' non sono necessariamente numeri primi ma sono certamente dispari oppure tutti numeri
pari.
l'algoritmo procede come segue:
1) x = (a'' + a') / 2, y = (b'' + b') / 2
2) xy = p oppure (p è divisibile per x o per y) ?
2.1) se si abbiamo trovato la soluzione a = x, b = y (oppure x o y) Fine
2.2) altrimenti xp < p
2.2.1) se si poniamo a' := x, b' := y e torniamo al punto 1)
2.2.2) se no poniamo a'':= x, b'' := y e torniamo al punto 2)
la velocità dell'algoritmo dipende da come scegliamo p', p'' che ovviamente dovrebbero essere abbastanza
vicini a p, per questo motivo possiamo utilizzare come fattori di p', p''
la cosa più semplice è considerare p' = p-1, p'' = p+1, nel caso in cui p non sia un numero pari.
28
Esempio:
p = 91 = 13*7
p' = 91 +1 = 92 = 23 * 4
p'' = 91 -1 = 90 = 9 * 10
ora (23+9)/2 = 16 (non è la soluzione 16 = 13*2), (4+10)/2 = 7 (è la soluzione)
variante: a' = b', a'' = b''
L'approccio combinatorio - economico del problema
Guardiamo la cosa da un altro punto di vista. Supponiamo di poter disporre di molti calcolatori in rete e di
poter distribuire l'enorme carico di elaborazione dati tra questi computer per trovare velocemente la
soluzione al problema della fattorizzazione di grandi numeri (RSA). E' possibile ? Di quanti pc avrò bisogno ?
E' conveniente dal punto di vista economico ? Sia n il numero da fattorizzare. Ci basa trovare un fattore. Per
Fermat sappiamo che una soluzione deve essere minore della radice quadrata di n. Sia allora W il numero di
cifre della radice quadrata di n.
P = il numero di calcolatori in rete
C = numero di combinazioni (possibili soluzioni intere al problema, cioè possibili divisori di n)
che ogni calcolatore può valutare ogni secondo (o ogni unità di tempo)
29
T = secondi o (altra unità di tempo)
Q = numeri di cifre della radice quadrata di n
n = ab numero da fattorizzare
vale la relazione P*C*T = 10^Q
10^Q è il numero delle disposizioni con ripetizione di 10 numeri su k posti
a questo punto si sia j il costo medio unitario di ogni PC occorre valutare che il costo totale dei
PC in rete non superi una certa ben definita quota oltre la quale non converrebbe implementare
il sistema (sum(jC) < M). Infine il fattore tempo. T < Tmax perché occorre fissare un limite
massimo ragionevole oltre il quale non ha senso andare. Considerando tutte queste condizioni
possiamo progettare un sistema di calcolo distribuito
Fattorizzazione e ricerca operativa
Possiamo vedere le cose anche da un altro punto di vista, dal punto di vista della ricerca operativa
(programmazione non lineare). Il nostro problema diventa un problema di programmazione non lineare a
variabili intere:
30
funzione obiettivo P = X1 X2
variabili: X1, X2
vincoli: X1, X2 >0 e interi
e applicare i metodi della ricerca operativa e/o i software già predisposti per questo tipo di problemi
31
Fattorizzazione per differenza dei fattori
Se p  xy allora è ben evidente che: 0  x  y 
possiamo considerare anche
Ora x = p/y e x-y = k
p
 2 essendo 2 il primo possibile fattore (ingenerale
2
p
 q ove q è tale che non esiste nessun fattore di p minore o uguale a q .
q
 k  k2  4p
troviamo che y  yk  p  0 con y 
dove possiamo
2
2
considerare k crescente (k = 0, 1, 2, …) o decrescente (K = p/2 –2, k =k-1, ……)
Se invece vogliamo trovare x y = p/x, quindi
x 2  xk  p  0 con x 
k  k2  4p
dove possiamo
2
considerare k crescente (k = 0, 1, 2, …) o decrescente (K = p/2 –2, k =k-1, ……)
Dal fatto che 0  x  y  p / 2  2 e che
2 p  x  y  p troviamo facilmente che
Anche in questo caso se stiamo trattando un problema RSA poniamo
x
p x
3
p  1.
4
k  k2  4p
 W che porta a
2
k 2  4 p  (2W  k ) 2
k  4p  0
2
unito a k  4 p  0
2W  k  0
2W  k  0
2
se
x
k  2W  0
k  k2  4p
 W ho che
(k  2W ) 2  k 2  4 p
2
 k  2W  0
 k  k2  4p
 W allora
nel caso in cui x 
(k  2W ) 2  k 2  4 p
2
32
ed infine l’ultimo caso
x
 k  k2  4p
 W mi porta a
2
k2  4p  0
k  4p  0
unito a 2W  k  0
2W  k  0
k 2  4 p  (2W  k ) 2
2
33
LISTATO IN PARI/Gp
{diff1(p) =local(k, y, x);
k = 0;
y = (-k + sqrt(k^2+4*p))/2;
x = (-k - sqrt(k^2+4*p))/2;
while (truncate(p/y) != (p/y) && truncate(p/x) != (p/x) ,
k=k+1;
y = (-k + sqrt(k^2+4*p))/2;
x = (-k - sqrt(k^2+4*p))/2);
print(y);
print(x);
return(1);}
Fattorizzazione per individuazione dell’intervallo migliore
Partendo dalla già nota relazione
x2  y2
 xy e ponendo y = x+a arriviamo a risolvere una disequazione
2
di secondo grado le cui soluzioni sono:
 a  4 p  a2
 a  4 p  a2
2
con 4 p  a  0
x
x
2
2
Nell’ipotesi invece che y = x-a ho che
a  4 p  a2
a  4 p  a2
2
con 4 p  a  0
x
x
2
2
Il problema è capire quale valore di a assegnare. Nei problemi RSA le radici non sono né troppo vicine tra
loro né troppo lontane quindi un buon valore per a potrebbe essere
Stesso discorso se partiamo da
per y = x-a ottengo che
x
a p
( x  y) 2  4 p :
a2 p
a2 p
a2 p
a2 p
per y = x+a x 
,x 
,x 
2
2
2
2
34
Teoria dei grandi numeri
Come è possibile gestire in un normale calcolatore numeri molto grandi, diciamo numeri interi
a 200 cifre ? Vediamo l'algoritmo con un esempio e poi generalizziamo con il formalismo matematico
Supponiamo di voler calcolare 321*44 = 14124
sappiamo che ogni numero intero lo possiamo scrivere nella sua notazione polinomiale:
(3x 2  2 x  1)(4 x  4)
con X = 10
svolgiamo la moltiplicazione tra i polinomi e consideriamo che 12 mod 2 = 2 e che 12-(12 mod
10) = 10 (per i coefficienti del polinomio prodotto usiamo l'aritmetica modulo 10 ovvero
se abbiamo coefficienti maggiori o uguali a 10 cioè ad esempio 12 = 10 +2 scriviamo 12 = X+2
per poi continuare a semplificare e a ridurre modulo 10 finché tutti i coefficienti del polinomio
sono in base 10)
tralasciano i passaggi abbiamo che 1x  4 x  1x  2 x  4 cioè 14124 che è la soluzione
4
3
2
Il caso della somma è ancora più semplice perché
35
3x 2  2 x  1  4 x  4  3x 2  6 x  5 cioè 321 + 44 = 365 (anche per la somma se ce ne fosse stato
bisogno avremmo dovuto ridurre i coefficienti del polinomio in base l'aritmetica modulo 10)
Idem è il caso della differenza tra numeri
Questo ci permetterà di programmare un calcolatore per fargli compiere operazioni molto complesse che un
normale PC non riuscirebbe a fare. Infatti dall'algebra elementare esistono formule che generalizzano la
somma, la differenza la moltiplicazioni e la divisione tra polinomi di qualunque grado
h
k
 (ri x i )   (ui x i ) 
i 0
i 0
h
max( h , k )
 (r  u ) x
i 0
i
i 0
i
i 0
i
i
hk
k
 r x u x  (  r u
i
i
i
j 0 i  p  j
i
p
)x j
caso con la virgola:
12,6 +15,4 = x  2 
3
4
 x  5   2x  7  1  2x  8
x
x
Il caso della divisione è un po',più complesso anche se in realtà una divisione non è altro che una serie di
sottrazioni come una moltiplicazione non è che una serie di somme
36
Ipotesi di Goldbach
La seguente trattazione non è la vera dimostrazione della congettura (la congettura non è stata
ancora dimostrata) ma solo il tentativo di fare alcuni ragionamenti intorno alla congettura
stessa.
LA CONGETTURA: Ogni numero pari maggiore di due è somma al più di due numeri primi non
necessariamente diversi tra loro
Primo tentativo di dimostrazione
Sia data la funzione Phi di eulero
 (q ) che mi dà il numero di primi con q minori di q.
E’ facile provare che
a)
 (q ) è sempre pari qualunque sia q
b)
 (q)  q  1
sse q è primo
PRIMO TANTATIVO DI DIMOSTRAZIONE (per induzione)
1) assumiamo che 2a = p+q vera, p, q primi
37
2)
2a   ( p1 )   (q1 ) un numero pari è sempre la somma di due numeri pari
 ( p1 )  p1  1 sse p1
è primo;
3)
2a  p1  1  q1  1
4)
2(a  1)  p1  q1 vera
 (q1 )  q1  1 sse q1
è primo. Allora
5) per induzione 2a = p+q per ogni a (ad ogni a cambieranno p, q)
SECONDO TENTATIVO DI DIMOSTRAZIONE (dimostrazione diretta)
Sia n = pq con p, q primi. Possiamo anche considerare n = 2pq perché
 (2 pq)   ( pq)
 (q ) è sempre pari e  ( pq)   ( p) (q) perché MCD(p,q) = 1
 ( pq)   ( p) (q)  ( p  1)( q  1)) pq  ( p  q)  1
 (n)  2k  pq  ( p  q)  1
pq+1-2k = p+q e dato che pq+1 è pari perché pq è dispri pq+1-2k è pari perché differenza di
numeri pari, quindi pq+1-2k è un generico numero pari che è somma di due primi p, e q.
38
ora questo ci indica una strada per costruire numeri primi:
risolviamo il sistema
pq+1-2k = m p+q = m
dove m è un generico numero pari e p, q sono le incognite mentre k è un parametro intero.
Svolgendo i calcoli e le opportune sostituzioni abbiamo
q 2  mq  2k  m  1  0, p  m  q
m  m 2  4m  4  8k
q
2
2
m  4m  4
k
8
a questo punto dovremmo essere in grado di sviluppare un applicativo tale che per ogni numero pari m mi
generi almeno due numeri p, q primi. Ciclando per tutti i pari avremo tutti i numeri primi . In realtà ci si
rende ben presto conto che con questo sistema si ottengono non solo le coppie di primi ma anche le coppie
di dispari la cui somma è m (si veda più in basso l'impostazione geometrica del problema)
ecco l'applicativo in C++:
#include <stdio.h>
#include <iostream.h>
#include <math.h>
int main(int argc, char *argv[])
{
long double p, q, m, k;
long double v, w;
int i, temp;
cout << "inserisci un numero pari ";
cin >> m;
39
k = int((pow(m,2)-4*m+4)/8);
do
{
q = (m + sqrt(pow(m,2)-4*m+4-8*k))/2;
p = (m - sqrt(pow(m,2)-4*m+4-8*k))/2;
k = k-1;
} while ((q != int(q)) || (p != int(p))) ;
v = m-q;
w = m-p;
cout << "fattore " << p << "\n";
cout << "fattore " << q << "\n";
cout << "fattore " << v << "\n";
cout << "fattore " << w << "\n";
cin >> "inserisci numero " >> temp;
return 0;
}
Si possono costruire altri programmi che sono varianti anche migliori di questa (le coppie dei numeri trovate
non sono necessariamente prime). In alternativa è sempre possibile partire da un numero pari diciamo 2m e
poi sottrarre 1, 2, 5, 7,...tutti i dispari e controllare poi le coppie così ottenute.
Si potrebbe usare l'equazione di secondo grado
x  sx  p  0 x1, 2
2
s  s2  4 p
s2
con p 

2
4
quindi possiamo scrivere un programma che accetta S in ingresso come numero pari e in output ci dà
coppie x, y con x+y = s
#include <stdio.h>
#include <math.h>
40
#include <iostream.h>
int main(int argc, char *argv[])
{
double x, y, a;
long s, p;
cout << "inserisci un numero pari ";
cin >> s;
for(p=int(pow(s,2)/4); p>0; p--)
{
x = (s + sqrt(pow(s,2)-4*p))/2;
y = (s - sqrt(pow(s,2)-4*p))/2;
p = p-1;
if (x == int(x) && y == int(y))
{
cout <<"------------------------" << "\n";
cout << " numero: " << x << "\n";
cout << " numero: " << y << "\n";
cout <<"------------------------" << "\n";
}
}
TERZO TENATIVO DI DIMOSTRAZIONE (dimostrazione per assurdo)
consideriamo l'approccio della dimostrazione per assurdo. supponiamo cioè di negare la tesi ovvero che
esiste un numero pari che non può essere somma di due numeri primi. Sia allora 2a il più piccolo numero
pari che non può essere scritto come 2a = p+q con p, q primi. Dunque 2a-2 è pari e può essere scritto
come 2a-2 = p+q con p, q primi, allora 2a = 2+p+q
caso 1) 2+p è primo con p primo allora arriviamo all'assurdo 2a = P + q con P= 2+p P, q primi e il teorema
è dimostrato
caso 2) 2+q + primo con q primo allora arriviamo all'assurdo 2a = p + Q con Q = 2 +q con p, Q primi e il
teorema è dimostrato
41
caso 3) 2+q non è primo né 2+p, allora si potrebbe cambiare la coppia p, q (es 10 = 7+3 = 5+5) e vedere
se si verificano i casi 1) 2). Qui il problema è più complesso perché si lega ad un'altre ben nota congettura
che vuole che i numeri primi si distribuiscano più facilmente nella forma p, p+2 con p primo. Nel sottocaso
che p=q abbiamo che 2a = 2+2p quindi 2a = 1+(2p+1).
QUARTO TENTATIVO DI DIMOSTRAZIONE (usando il Teorema di Fermat)
a p  a(mod p)
a  a(mod q)
q
allora a
2
 a p q (mod pq)
da cui possiamo dedurre che 2k = p+q ?
Nota: non dobbiamo provare che la somma di due primi è un pari (questo è banale perché due primi sono
sempre due numeri dispari altrimenti sarebbero divisibili per 2 e la somma di due dispari è sempre un
numero pari), infatti
p+q = 2b sempre (partendo da p e q noti, 2a = 2p' +1 + 2q' +1 per opportuni p', q' interi )
QUINTO TENTATIVO DI DIMOSTRAZIONE
Consideriamo il numero pari 2*a . Per il teorema della decomposizione unica in fattori sappiamo che tale
numero si può sempre scrivere come una somma (non necessariamente unica) di numeri primi e che questa
somma deve essere costituita da un numero pari di addendi (altrimenti il risultato sarebbe dispari). Esempio:
30 = 3*10 = 3+3+3+3+3+3+3+3+3+3 = 5*6 = 5+5+5+5+5+5. Supponiamo che 2*a = p+q+r+s (con
42
p, q, r, s numeri primi). Abbiamo preso 4 numeri primi ma il ragionamento sarebbe stato ugualmente valido
per 6, 8, 10 numeri primi. Dunque 2*a –(r+s) = p+q ma r+s = 2b per un certo b quindi 2(a-b) = p+q.
Fissato a tramite la decomposizione unica in fattori primi mi determino una classe finita di possibili valori di b
e al variare di a 2(a-b) mi determinano l’insieme dei numeri pari. Quindi ho provato che il generico numero
pari 2(a-b) lo posso sempre scrivere come somma di due primi p, q. Nell’ esempio di prima 30 =
5+5+5+5+5+5 => 30 – 5+5+5+5 = 5+5. => 10 = 5+5; 30 –3-3-3-3-3-3-3-3 = 3+3 0> 6 = 3+3
Osservazioni:
- non è vero che ogni numeri pari aumentato di una unità è un numero primo ma è sempre vero
che un numero primo diminuito di una unità è un numero pari, quindi esistono infiniti numeri
pari (non tutti), che aumentati di una unità danno un numero primo
-un numero pari è sempre la somma (o differenza) di due numeri dispari oppure è la somma di
due pari; l'insieme dei numeri dispari comprende l'insieme dei numeri primi
- l'unico numero primo pari è il 2 (è un primo un po' speciale)
- possiamo considerare 1 un numero primo (è un primo un po' particolare)
43
Impostazione geometrica del problema
Consideriamo un numeri pari e i un piano cartesiano rappresentiamo tale numero formando con le ascisse e
le ordinate un quadrato. Consideriamo la diagonale del quadrato: nella figura le x sono nella diagonale le
caselle gialle ottenute dall'intersezione tra i numeri primi delle ascisse (in giallo) e le ordinate (in giallo)
minori del numero pari dato. Questo ci suggerisce un metodo iterativo per costruire la tavola dei numeri
primi perché a partire dai primi numeri primi diagonale dopo diagonale si trovano i primi successivi. Vediamo
meglio questo concetto.
6
5
Coppia primi
4
x
Coppia primi
3
2
x
1
Coppia primi
1
2
3
4
5
6
a) prendiamo in considerazione tutte le coppie i, j tali che i +j = 2a per un certo a fissato
b) prendiamo solo in considerazione quelle coppie tali che MCD (i,j) = 1 e la coppia speciale i=j
c) escludiamo le coppie che contengono l'unità.... le rimanenti coppie sono coppie di primi ? No
in generale ma se procediamo in modo ricorsivo a partire dal primo numero pari e per ogni pari
con questo metodo determiniamo i primi numeri primi minori di quel numero pari nelle
44
successive diagonali possiamo escludere quei casi in cui mcd(i,j)= 1 i+j = 2a ma uno dei due (i
o j) non è primo (ovvero per ogni diagonale calcoliamo i primi e ne teniamo in considerazione
per le diagonali successive - un po' come il crivello di Eratostene.)
d) con questo metodo costruttivo iterattivo possiamo dire che nella diagonale c'è sempre
qualche coppia di primi ? In realtà nella diagonale troviamo tutte le possibili coppie i, j tali che i +j = 2a.
Le coppie devono essere o coppie di pari o coppie di dispari. Dobbiamo provare che tra le coppie di dispari
c'è almeno una coppia di primi.
10
9
no
8
x
7
Primi
6
x
5
Primi
4
x
3
Primi
2
x
1
no
1
2
3
4
5
6
7
8
9
10
la diagonale è sempre simmetrica e questo ci permette di procedere più veloci
45
visualizzazione multipla (si possono intravedere interessanti geometrie ?)
10
9
no
8
7
x
primi
6
5
x
primi
Primi
x
x
Primi
2
1
x
Primi
4
3
Primi
primi
primi
Primi
x
Primi
1
x
primi
2
Primi
x
x
primi
3
4
5
Primi
6
no
7
8
9
10
crivello di Eratostene (formulazione grafica: le x sono i primi perché non hanno intersezioni con "gialli")
14
13
Primo
12
11
Primo
10
9
8
7
Primo
6
5
Primo
4
3
2
Primo
1
1
2
3
4
5
6
7
46
Giocare in borsa con la matematica
Molti matematici ritengono che l'analisi tecnica (tanto cara agli economisti e alle banche) non sia un valido
strumento di previsione. Forse hanno ragione, forse no.
L'idea è allora quella di proporre (algoritmi un po' strani e fantasiosi) che però potrebbero essere efficaci in
molte situazioni
Supponiamo di considerare che X sia una variabile casuale. X rappresenta il valore di una certa azione al
variare del tempo. Consideriamo i valori di X per circa 30 sedute di borsa consecutive (un mese e mezzo
di contrattazioni).
Calcoliamo la media e lo scarto quadratico medio di X cioè  ,  . Questa può in effetti essere una
forzatura ma possiamo accettare l'ipotesi valida. Per giustificarla potremmo dire che in un
determinato periodo temporale (periodo che comprende anche le previsioni a breve ovvero
periodo totale = periodo dati + periodo previsione) la variabile casuale X assumerà dei valori
x1.....xN, con probabilità p1........pN tale che la somma delle probabilità pi sia pari a 1.
Utilizziamo il teorema di Chebicev che dice che data una qualunque variabile casuale X vale la seguente
relazione:
P(   k  X    k )  1 
1
k2
cioè
47
P(| X   | k ) 

i
1
k >0
k2
xi
n
( xi   ) 2
 
n
i
2
Ove P è la probabilità che la variabile casuale X assuma certi valori in un intervallo di dati.
Impostiamo il livello di affidabilità al 95% cioè 1 
1
 0.95 e troviamo K (possiamo fare altre scelte dl
k2
tipo 90% o 98%, troveremo valori di k differenti). Più aumentiamo il livello di affidabilità più aumenta anche
il range cioè l'intervallo in cui il valore della nostra azione può oscillare per il prossimo mese di contrattazioni.
Diminuendo la percentuale si rischia di fare previsioni poco attendibili.
Con queste considerazioni stimiamo che il valore della nostra azione oscillerà nel prossimo mese di
contrattazioni in un determinato intervallo a < X < b con una certa probabilità.
Ovvio che la previsione del valore del titolo deve essere limitata nel tempo in quanto i parametri della
variabile casuale andrebbero ricalcolati alla fine di ogni giornata borsistica. Ma tanto per semplificare
supponiamo di fare una previsione per un periodo temporale di circa un mese
48
se si potesse stimare la probabilità p che un titolo scenda o salga in un ben determinato periodo (o q la
probabilità opposta p+q =1) non sarebbe una idea malvagia considerare la distribuzione di Bernulli e dire
che la probabilità che in n sedute di contrattazioni ci siano k rialzi del titolo è:
n
Pn,k    p k q n k
k 
ove p+q = 1, e dove la variabile casuale ha media = np e varianza = npq. Se riusciamo a ben stimare
p e q riapplicando il teorema di Chebicev possiamo avere delle informazioni in più sul possibile andamento
del nostro titolo. Possiamo calcolare p e q supponendo di studiare il titolo per 30 sedute di borsa consecutive
p = numero di sedute positive /30, q = numero di sedute negative / 30, la media è facilmente calcolabile
np  3  X  np  3
np  3 npq  X  np  3 npq
Posso considerare un portafoglio finanziario formato da n titoli, impostare un valore C da investire e cercare
le quantità che devo acquistare di ogni singolo titolo in modo da massimizzare il mio investimento (problema
di ricerca operativa)
49
I piani di accumulo del capitale
Molte strategie di investimento si basa sui piani di accumulo del capitale. L'idea che voglio proporre è quella
di usare la serie geometrica per progettare un piano di accumulo. Di solito i tradizionali piani prevedono un
investimento costante, usando la serie aritmetica o quella geometrica possiamo considerare interessanti
varianti
S = somma da investire
n = numero delle sedute di borsa da considerare = periodo di investimento
a = valore iniziale da investire
1  q n1
S  a  aq  aq  ....  aq  a
1 q
2
n
G1  aq i (termine ennesimo)
ad ogni seduta investirà il termine:
a  Gi  b a cui impongo dei limiti fissati
Se penso che la tendenza si al rialzo una strategia prudente è 0<q<1 (se ci fossero delle chiusure in
"negativo" la perdita sarebbe limitata)
50
Se penso che la tendenza sia al ribasso una strategia prudente è q>1 (al primo "rimbalzo tecnico" si
recuperano tutte le perdite)
Nel caso delle progressioni aritmetiche:
S  a  (a  q)  (a  2q)  ....  (a  nq) 
(n  1)( 2a  nq)
2
Gi  a  id
il vero problema è come scegliere i parametri in modo da ottimizzare i guadagni e ridurre la perdite
supponendo di sapere la "tendenza del mercato". L'argomento merita un approfondimento. Non tutti sono
concordi con queste teorie ed esistono comunque pareri discordi.
Il Lotto e la matematica
Non esistono teoria sicure sul gioco del lotto. Qui vogliamo presentare un semplice programma in Visual
Basic .Net per la generazione di numeri casuali per giocare al Lotto e tentare la fortuna. Chi vende i numeri
"fortunati" spesso altro non fa che usare sistemi come questo (sistemi che non garantiscono in nessun caso
vincite)- Il listato si può modificare per adattarlo anche ad altri linguaggi di programmazione come il C/C++.
LISTATO IN VISUAL BASIC .NET
Module Module1
Sub Main()
Dim generator As New Random
Dim arr(30) As Integer
51
Dim randomValue As Integer
Dim ruota As String
Dim i As Integer
Console.WriteLine("inserisci la ruota")
ruota = Console.ReadLine()
Console.WriteLine(ruota)
For i = 0 To 4
randomValue = generator.Next(1, 90)
arr(i) = randomValue
Console.Write(arr(i))
Console.Write("-")
Next
Console.ReadLine()
End Sub
End Module
52
Sommario
Fattorizzare i numeri interi ................................................................................................................................ 1
Considerazione preliminare (algoritmo 0)..................................................................................................... 1
Primo algoritmo (AL-1) (variante della fattorizzazione alla Fermat) ............................................................. 3
Secondo algoritmo (Al-2) ............................................................................................................................... 7
Terzo algoritmo (Al-3).................................................................................................................................. 12
Quarto algoritmo (Al-4) ............................................................................................................................... 15
Quinto algoritmo (Al-5) ............................................................................................................................... 18
Sesto algoritmo (Al-6) .................................................................................................................................. 21
Fattorizzazione con le disequazioni ............................................................................................................. 22
Fattorizzazione con il teorema di Bezout .................................................................................................... 25
Fattorizzazione con i logaritmi .................................................................................................................... 26
Fattorizzazione con il metodo della bisezione ............................................................................................ 28
L'approccio combinatorio - economico del problema ................................................................................ 29
Fattorizzazione e ricerca operativa ............................................................................................................. 30
Fattorizzazione per differenza dei fattori ................................................................................................... 32
Fattorizzazione per individuazione dell’intervallo migliore ....................................................................... 34
Teoria dei grandi numeri ................................................................................................................................. 35
Ipotesi di Goldbach .......................................................................................................................................... 37
Impostazione geometrica del problema ..................................................................................................... 44
Giocare in borsa con la matematica ................................................................................................................ 47
I piani di accumulo del capitale ....................................................................................................................... 50
Il Lotto e la matematica ................................................................................................................................... 51
Sommario ........................................................................................................................................................ 53
53