Esercitazione 1
Come verifica del lavoro fatto fin qui, proponiamo i seguenti quesiti sui vari moti rettilinei.
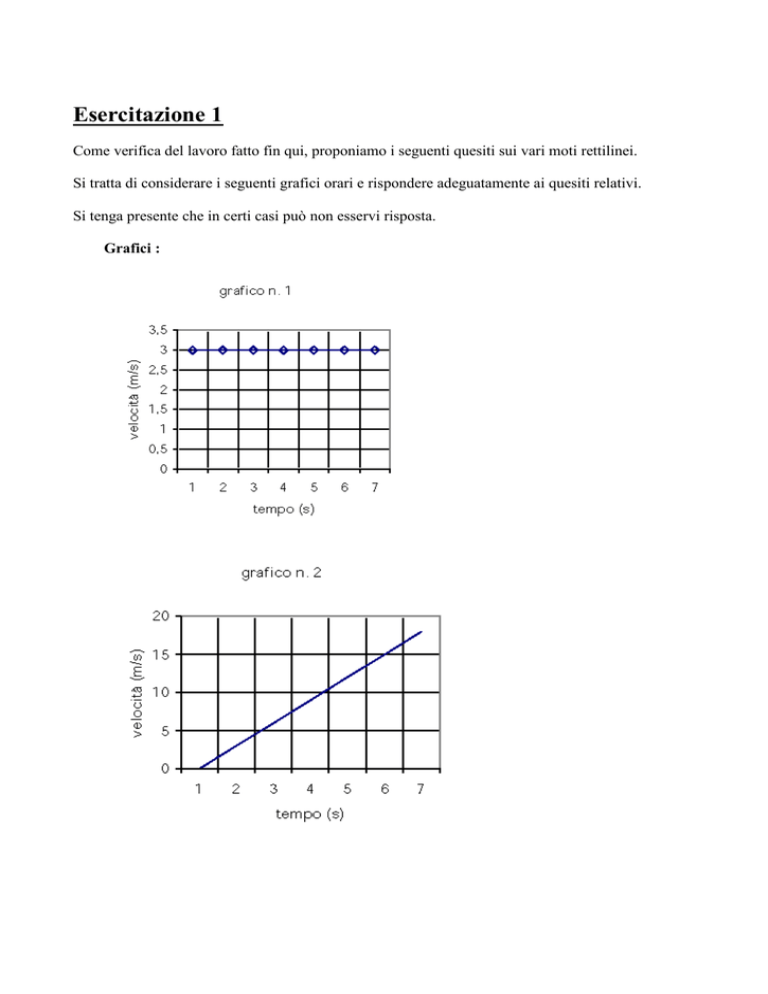
Si tratta di considerare i seguenti grafici orari e rispondere adeguatamente ai quesiti relativi.
Si tenga presente che in certi casi può non esservi risposta.
Grafici :
Quesiti :
Grafici 1 e 2 :
a) tipo di moto ?
b) velocità ?
c) spazio percorso fra il tempo t = 2,5 s ed il tempo t = 4,5 s ?
Grafici 3 , 4 , 5 , 8 , 9 :
a) tipo di moto ?
b) velocità dopo 4 s ?
c) spazio percorso fra il tempo t = 2 s ed il tempo t = 5 s ?
Grafici 6 , 7 , 10 , 11 , 12 :
a) tipo di moto ?
Risposte :
Si tenga presente che, anche se non esplicitamente dichiarato, i moti in questione sono tutti moti
rettilinei.
1 - a : moto rettilineo uniforme
1 - b : v = 3 m/s
1-c:s=3·2=6m
2 - a : moto rettilineo uniformemente accelerato
2 - b : velocità variabile (cresce uniformemente)
2 - c : area del trapezio, s = (10 + 5) · 2 / 2 = 15 m .
Si può usare anche la nota formula
con l'avvertenza di porre lo spazio
iniziale uguale a 0 e di fare ripartire il tempo all'istante t = 2,5 . La velocità iniziale è
deducibile
direttamente dal grafico mentre l'accelerazione deve essere calcolata prendendo una
qualunque
differenza di velocità rispetto ad un qualunque intervallo di tempo.
3 - a : moto rettilineo uniformemente accelerato con accelerazione negativa
3 - b : è negativa ed è legata alla "pendenza" del grafico al tempo t = 4 s
3 - c : s = 20 - 35 = -15 m , il moto avviene in modo contrario alla direzione dello spazio
4 - a : moto rettilineo uniforme con velocità positiva
4 - b : la velocità è costante in ogni istante e vale v = (70 - 10) / (7 - 1) = 60 / 6 = 10 m/s
4 - c : s = 50 - 20 = 30 m
5 - a : moto rettilineo uniforme con velocità negativa
5 - b : la velocità è costante in ogni istante e vale v = (0 - 5) / (6 - 1) = -5 / 5 = -1 km/minuto =
= -1000 / 60 m/s = -16,6 m/s circa
5 - c : s = 1 - 4 = -3 km = -3000 m
8 - a : moto rettilineo uniformemente accelerato con accelerazione negativa
8 - b : 6 m/s
8 - c : area del trapezio, s = (10 + 4) · 3 / 2 = 21 m
9 - a : moto rettilineo uniforme con velocità negativa
9 - b : la velocità è costante in ogni istante e vale v = (0 - 12) / (7 - 1) = -12 / 6 = -2 m/s
9 - c : s = 4 - 10 = -6 m
6 - a : moto rettilineo uniformemente accelerato con accelerazione positiva
7 - a : moto rettilineo uniformemente accelerato con accelerazione a = 3 m/s²
10 - a : moto rettilineo vario con accelerazione positiva decrescente
11 - a : moto rettilineo vario con velocità positiva crescente fino al tempo t = 7 s poi moto
rettilineo
uniforme con velocità v = 40 m/s
12 - a : moto rettilineo uniformemente accelerato con accelerazione negativa fino al tempo t = 7 s
poi
stato di quiete con spazio s = 40 m
A questo punto, dopo avere risolto tutti i quesiti, sorge spontanea una ulteriore domanda :
"com'è la risultante delle forze applicate al corpo nei singoli grafici? (nulla, costante diversa da
zero,
variabile)"
Esercitazione 2
Problemi :
- 1 - Una bambina di 15 kg su un carrello di 9 kg sta scendendo lungo una discesa ad una
velocità costante di 2 m/s. Un suo fratello di 20 kg, fermo lungo la discesa, sale
anch’esso
sul carrello quando questo gli passa accanto. Con quale velocità proseguono i due
ragazzi
con il carrello?
- 2 - Uno studente siede su una piattaforma girevole attorno ad un asse verticale. Egli tiene
le braccia abbassate con in ciascuna mano un oggetto di massa m = 4 kg. L’istruttore
lo pone in rotazione con una velocità angolare pari a 6,28 rad/s. Si trascurino le forze
di attrito e si supponga che rispetto all’asse di rotazione non agisca nessun momento
meccanico. Si assuma anche che il momento d’inerzia dello studente rimanga costante
e
pari a 5,0 kg.m2 indipendentemente dalla posizione delle braccia. La variazione di
momento
d’inerzia quando questi allarga le braccia tenendole tese orizzontalmente sarà quindi
dovuta
solo alla variazione della distanza dei pesi dall’asse di rotazione, che inizialmente è di
soli
15 cm, e, a braccia tese orizzontalmente, è di 90 cm. Trovare la velocità angolare
finale
dello studente.
- 3 - Evidenziare le analogie fra i due problemi.
- 4 - Un allenatore spinge un ciclista, inizialmente fermo e che non pedala, su di un percorso
orizzontale lungo 10 m, con una forza F = 40 N. Calcolare il lavoro compiuto,
considerando
trascurabili gli attriti.
- 5 - Che tipo di moto sarà quello del ciclista durante la spinta? Utilizzando la formula dello
spazio per questo moto e la formula della seconda legge della dinamica, si dimostri che
il lavoro fatto dall’allenatore vale : L = ½ mv2.
Soluzioni :
-1testo)
La velocità con cui scende inizialmente la bambina è costante (come si deduce dal
quindi sul sistema carrello-bambina non agiscono forze esterne o, meglio, la risultante
delle forze esterne è nulla. Questo si verifica perché la pendenza del piano inclinato è
tale per cui l'attrito, a cui il carrello è soggetto, è controbilanciato dalla forza peso del
sistema carrello-bambina.
Quando il fratello sale sul carrello, il peso del sistema carrello-bambina-fratello cresce
di
conseguenza ma cresce anche l'attrito subito dal carrello in modo tale che la risultante
delle
forze è ancora nulla e quindi il sistema continua a muoversi con velocità costante anche
se
diversa dalla velocità iniziale (lasciamo al lettore volenteroso la dimostrazione che
l'attrito
è controbilanciato dal peso anche dopo la salita del fratello).
Detto questo, possiamo considerare il sistema carrello-bambina-fratello-fermo prima ed
il
sistema carrello-bambina-fratello dopo come un sistema isolato per il quale vale il
principio
di conservazione della quantità di moto.
Applicando questo principio possiamo scrivere :
dove
è la massa della bambina,
quella del carrello,
è la velocità iniziale con cui scende la bambina,
quella del fratello,
è la velocità iniziale del fratello e
è la velocità finale del sistema dopo che è salito il fratello.
Poiché inizialmente la velocità del fratello
è nulla, la formula si riduce a :
da cui è facile ricavare la velocità finale desiderata :
.
Sostituendo i dati numerici si ottiene :
(dove il simbolo
significa "uguale circa").
- 2 - Se su un corpo ruotante attorno ad un asse non agiscono momenti di forze esterne
(o la loro risultante è nulla) il suo momento angolare si conserva. Nel nostro caso,
il momento angolare prima e dopo che lo studente allarghi le braccia non cambia pur
cambiando il momento d'inerzia del sistema studente-pesi.
Il momento d'inerzia di un singolo peso, in questo semplice caso, vale :
dove m è la massa ed r è la distanza del peso dall'asse di rotazione.
Il momento angolare (che si conserva nel tempo) è :
dove
è la velocità angolare di rotazione.
Possiamo allora scrivere :
dove
approssimando,
è il momento d'inerzia del ragazzo (sia con le braccia giù che,
con le braccia allargate),
è il momento d'inerzia dei pesi quando il ragazzo tiene
le
braccia giù,
è la velocità angolare di rotazione iniziale (quando lo studente ha le
braccia
giù),
è il momento d'inerzia dei pesi quando il ragazzo tiene le braccia allargate e
è la velocità angolare finale (quando il ragazzo tiene le braccia allargate).
Dalla formula scritta sopra possiamo ricavare direttamente la velocità angolare finale :
.
Sostituendo i valori numerici otteniamo :
(il fattore 2 sopra e sotto la linea di frazione dipende dal fatto che i pesi che lo
studente
tiene in mano sono due).
-3-
Il primo è un problema di dinamica traslazionale (moti su di una retta). Il secondo è di
dinamica rotazionale. Li abbiamo risolti applicando al primo il principio di
conservazione
della quantità di moto ed al secondo il principio di conservazione del momento
angolare.
La quantità di moto vale :
mentre il momento angolare vale :
.
L'analogia fra i due problemi consiste nel fatto che le formule scritte sopra sono
"simili".
Alla massa m corrisponde il momento d'inerzia I ed alla velocità lineare v
corrisponde
la velocità angolare
-4-
.
La forza applicata al ciclista è sulla direzione e verso del moto quindi il lavoro è dato da
:
.
- 5 - Supponendo che gli attriti siano trascurabili e dato che la forza che agisce sul ciclista è
costante,
il moto che ne deriva è un moto rettilineo uniformemente accelerato.
Considerando che al tempo 0 lo spazio percorso è 0 (cominciamo a misurare lo
spazio
percorso all'istante 0 ), la formula che dà lo spazio percorso in funzione del tempo è :
dove a è l'accelerazione costante con cui si muove il ciclista e t , nel nostro caso, è il
tempo
finale quando l'allenatore cessa di spingere.
D'altra parte, per il secondo principio della dinamica, sappiamo che :
dove F è la forza con cui l'allenatore spinge sul ciclista, m è la massa del sistema
bicicletta-ciclista e a è l'accelerazione a cui esso è soggetto.
Il lavoro compiuto dalla forza sarà allora :
che , se consideriamo che il termine
diventa :
è uguale alla velocità v raggiunta al tempo t ,
Esercitazione 3
01 - Esempio in fisica di rette passanti per un punto.
Consideriamo l'equazione :
.
Essa è formalmente identica all'equazione di una retta passante per un punto. Nel piano
cartesiano
0st essa rappresenta allora una generica retta di coefficiente angolare v che passa per il punto
:
Il significato fisico di questa equazione è che essa rappresenta il grafico orario tempo-spazio di un
moto uniforme dotato di velocità v con la proprietà che, qualunque sia la velocità (ovvero la
pendenza della retta) al tempo
il corpo si trova nello posizione
.
02 - Esempio in fisica di retta passante per due punti.
Consideriamo un corpo in moto rettilineo uniforme. Supponiamo che al tempo t = 1 il corpo
si trovi nello spazio s = 2 e poi al tempo t = 3 si trovi nello spazio s = 7 (i tempi siano misurati
come al solito in secondi e gli spazi in metri). Graficamente :
Possiamo riportare questi dati in un diagramma tempo-spazio :
Siccome il diagramma orario di un moto rettilineo uniforme è una retta (essendo la velocità del
corpo,
ovvero la pendenza del diagramma orario, costante in ogni punto) e siccome questa retta deve
passare
per i punti A e B :
potremo scrivere (avendo sostituito (nella formula di riferimento della retta per due punti) s al
posto
di y e t al posto di x ) :
e, sostituendo i valori numerici :
.
Facendo i calcoli si ottiene :
.
Moltiplichiamo ora ambo i membri per 5 e per 2 :
e semplifichiamo :
.
Dividiamo ambo i membri per 2 :
e semplifichiamo :
.
Sommiamo 2 ad entrambi i membri :
e semplifichiamo :
.
Moltiplichiamo, distribuendo, a destra dell'uguale :
e semplifichiamo :
.
Questa è l'equazione della retta e ridotta ai minimi termini.
Come verifica del risultato trovato notiamo che il coefficiente angolare è
e l'ordinata all'origine
è
e questo corrisponde abbastanza bene col grafico (l'imprecisione sull'ordinata all'origine
dipende dal fatto che il grafico è stato disegnato a mano libera) :
03 - Esercizio.
Si lascia cadere un sasso per misurare la profondità di una voragine. Dopo 4 s si sente il rumore
del
sasso che ha toccato il fondo. Calcolare la profondità della voragine e stimare l'entità dell'errore
(tenendo
presente che la velocità del suono nell'aria è circa 340 m/s ).
Soluzione approssimata.
Gettando un sasso dentro una voragine siamo in grado di stimarne la profondità misurando il tempo
dall'istante in cui lasciamo cadere il sasso all'istante in cui sentiamo il rumore del sasso che tocca il
fondo.
Questo tempo sia di t = 4 s .
Occorre subito dire che la valutazione della profondità della voragine con questo metodo non è
così semplice come potrebbe sembrare. Entrano difatti in gioco alcuni "particolari" che complicano
la stima. I più importanti di essi sono :
- 1 - la resistenza dell'aria : essa, se presa in considerazione nel calcolo della legge oraria
del moto del sasso, lo complica notevolmente
- 2 - il tempo di reazione dell'osservatore : il tempo cronometrato è sempre maggiore di
quello effettivo
- 3 - la velocità del suono : noi udiamo il tonfo del sasso un certo tempo dopo l'esatto istante
in cui esso ha toccato il fondo perché il suono ha una velocità non infinita
Tutti e tre questi fenomeni fanno sì che la stima della profondità fatta ignorandoli sia per eccesso.
Valutiamo ora la soluzione teorica in assenza di questi "errori".
Il sasso è soggetto alla forza peso costante
la cui intensità è
moto rettilineo uniformemente accelerato.
per cui esso cade di
L'equazione oraria di tale moto è :
.
Per comodità ci poniamo nella situazione in cui lo spazio iniziale e la velocità iniziale sono nulli
(semplicemente facendo scattare il cronometro quando lasciamo cadere il sasso senza dotarlo
di una velocità iniziale e misurando lo spazio verso il fondo della voragine dal punto in cui il
sasso è lasciato cadere).
Avremo quindi più semplicemente :
.
Sostituendo i valori numerici otteniamo :
(abbiamo chiamato h lo spazio percorso).
Valutiamo ora la soluzione reale considerando solo l'errore dovuto alla velocità del suono
( 340 m/s ). Per fare questo facciamo un ragionamento approssimato ma di semplice "traduzione"
matematica.
Consideriamo che il suono, dal fondo della voragine di profondità pari al valore teorico
precedentemente
calcolato, per pervenire all'orecchio dell'osservatore ci mette un tempo pari a :
( = tempo suono). Dobbiamo allora togliere dai 4 secondi complessivi questo tempo per trovare
il tempo effettivo che sarà :
(
= tempo effettivo).
A questo punto si rifà il calcolo della caduta con questo nuovo tempo e si ottiene :
.
Questo metodo di stima è solo approssimato !!! Lasciamo al lettore volenteroso il calcolo esatto
della stima ...
Questo problema ci dà anche un'idea in quello che è effettivamente il lavoro del fisico : valutare
tutti i
fenomeni in gioco e quantificarne l'importanza rispetto ad una eventuale soluzione teorica
semplicistica.
Soluzione esatta.
Il problema della valutazione della profondità di una voragine gettandoci dentro un sasso e
misurando
il tempo in cui il suono perviene al nostro orecchio (dal momento in cui esso viene lasciato cadere),
nel solo caso in cui si trascurano l'attrito con l'aria ed il tempo di reazione dell'osservatore (che
misura
il tempo con un cronometro), la volta scorsa è stato risolto con un procedimento approssimato.
Vediamo ora come il problema andrebbe risolto in modo esatto.
Il tempo in questione, da quando il sasso viene lasciato cadere al momento in cui il suono
dell'impatto
col terreno ci perviene, sia t = 4 s .
Questo tempo si compone di due parti. Il tempo
, da quando il sasso è lasciato cadere a quando
esso effettivamente tocca il terreno, e dal tempo
, corrispondente al tempo impiegato dal suono
a
pervenire all'orecchio dell'osservatore dal momento dell'impatto del sasso sul fondo. Possiamo
allora
scrivere :
.
Ricaviamo ora i due tempi.
Per il tempo
:
Siccome il sasso cade di moto rettilineo uniformemente accelerato (trascuriamo
l'attrito con l'aria) possiamo scrivere :
da cui, moltiplicando ambo i membri per 2 , dividendo per g e invertendo l'uguaglianza, si
ricava :
da cui, estraendo la radice quadrata in ambo i membri, si ottiene :
.
Per il tempo
:
Siccome il suono procede dal fondo della voragine di moto uniforme, possiamo scrivere :
quindi (essendo la velocità del suono nell'aria circa 340 m/s ) avremo :
da cui si ottiene :
(abbiamo diviso ambo i membri per 340 , moltiplicato per
Siamo ora in grado si sostituire le due espressioni di
e
ed invertito l'uguaglianza).
così trovate nell'equazione
ottenendo :
.
Questa è una equazione nell'incognita h (essendo g nota, pari a circa 9,8 m/s² ) non di primo
grado e
quindi più complessa da risolvere.
Omettiamo qui la soluzione ribadendo che qui ci interessava solo illustrare il procedimento esatto
con cui risolvere il problema. Quando avremo studiato le equazioni di secondo grado, saremo in
grado di risolvere esattamente l'equazione.
(la soluzione approssimata dell'equazione, eseguita al computer, fornisce il valore
)
04 - Calcolo della velocità finale di un corpo che cade.
La legge di conservazione dell'energia meccanica può essere utilizzata per calcolare direttamente
la velocità con cui un corpo, cadendo, tocca terra.
Essendo :
(energia cinetica finale = energia potenziale gravitazionale iniziale) possiamo scrivere :
Per ricavare v dividiamo ambo i membri per m e moltiplichiamo i medesimi per 2 :
.
Semplificando otteniamo :
e successivamente, estraendo la radice quadrata a destra ed a sinistra dell'uguale :
La formula trovata dà la velocità del corpo all'istante dell'impatto col terreno (trascurando l'attrito
con l'aria).
05 - Caduta in aria dalla stessa altezza di due sfere uguali ma di materiale diverso.
Un corpo di massa qualunque e forma qualunque cade nel campo gravitazionale terrestre ed in
assenza di aria con la stessa accelerazione g . Più corpi di massa e forma diverse cadono allo
stesso
modo, per cui, se lasciati cadere ad un certo istante dalla stessa altezza, essi toccano terra allo
stesso istante (in assenza di aria).
Prima :
Dopo :
Il moto che essi seguono è un moto rettilineo uniformemente accelerato di equazione oraria :
.
In presenza di aria la situazione cambia notevolmente. Il corpo è soggetto a più forze che
agiscono
su di esso contemporaneamente :
- la forza peso
che è diretta verso il basso
- la forza di Archimede (un corpo immerso in un fluido riceve una spinta verso l'alto pari al
peso del fluido spostato) che è rivolta verso l'alto e che vale
= costante (il peso
dell'aria spostata dipende dal volume del corpo e quindi, considerando il corpo rigido,
esso non cambia). Questa forza è molto importante se il corpo è leggero. Un palloncino
riempito di elio, per esempio non cade a terra, ma sale in alto !!!
- la forza di attrito con l'aria (detta anche forza di resistenza del mezzo) che è rivolta
verso
l'alto ed è approssimativamente proporzionale al quadrato della velocità del corpo. Essa
vale
- altre forze che dipendono dal fatto che il pianeta terra è un sistema ruotante per cui non è
un sistema di riferimento inerziale. Tali forze apparenti noi le trascureremo per esigenze
di
semplicità anche se esse sono importanti (Galileo stesso le prese in considerazione nei suoi
esperimenti di caduta dei gravi)
Riassumiamo in un grafico la situazione all'istante in cui il corpo inizia a cadere (la forza di attrito è
in
quell'istante nulla) :
(abbiamo posto le forze agenti separate per comodità).
Durante la caduta del corpo, la forza peso e la forza di Archimede rimangono costanti mentre la
forza di attrito cresce al crescere della velocità del corpo :
Osservando i due grafici si nota che la forza risultante che agisce sul corpo e che ne determina
l'accelerazione diminuisce durante la caduta. Ci sarà allora un certo istante in cui la forza risultante
diventa nulla. Da quell'istante in poi il corpo si muoverà di moto rettilineo uniforme !!! Lo sanno
bene i paracadutisti ...
Cosa succede se confrontiamo le cadute di due corpi sferici di ugual raggio ma di massa diversa
(per esempio uno di ferro e l'altro di legno) ?
Per il corpo più leggero si raggiungerà prima l'annullamento della forza risultante per cui esso
toccherà
terra più tardi e con minore velocità.
Riportiamo di seguito una simulazione al computer (ottenuta con tecniche di calcolo numerico)
della
caduta di corpi sferici di ugual raggio di massa 1 kg e 2 kg . Si tratta dei grafici orari tempo-spazio
dei moti nei due casi (i corpi cadono da un'altezza di 50 m ) :
Si noti che dopo un certo tempo i grafici diventano rettilinei, cioè le velocità diventano costanti
come
affermato sopra.
06 - Esercizio sulla conservazione dell'energia meccanica.
Consideriamo il presente problema tipico della "tecnologia" delle montagne russe :
Un carrello si trova in A con velocità
quale velocità
. L'altezza dal suolo di A è
esso raggiungerà il punto B ? La seconda quota è
. Con
. Riuscirà il carrello
a raggiungere C ? Se lo raggiungerà, che velocità avrà ? Se non lo raggiungerà, a quale altezza
esso arriverà ? Si considerino trascurabili gli attriti di ogni tipo. (la massa del carrello è m ).
Suggerimento :
- l'energia meccanica totale in A è :
- l'energia meccanica totale in B è :
- l'energia meccanica totale in C sarebbe :
Soluzione.
L'energia meccanica in A è :
.
L'energia meccanica in B è :
(essendo in B la quota nulla non vi è energia potenziale).
Trascurando gli attriti, per il principio di conservazione dell'energia meccanica, avremo :
cioè, sostituendo :
.
Da questa formula siamo in grado di ricavare
. Per fare questo operiamo alcune semplificazioni.
Moltiplicando ambo i membri per 2 e semplificando, abbiamo :
.
Raccogliendo m nel secondo membro otteniamo :
.
Dividendo ambo i membri per m abbiamo :
.
Da questa formula possiamo ricavare
da cui, sostituendo i valori numerici di
estraendo la radice quadrata da ambo i membri :
,
e
, otteniamo :
.
Vediamo ora se il carrello (sempre trascurando gli attriti) riesce a raggiungere C .
Consideriamo che il carrello, dopo avere oltrepassato il punto B , raggiunga la quota h con
velocità
nulla (perdendo cioè tutta la sua energia cinetica a scapito di quella potenziale) (si noti che, al
momento,
non sappiamo se h sarà maggiore della quota di C !!). Potremo allora scrivere :
(essendo la velocità alla quota h nulla e di conseguenza l'energia potenziale alla quota h uguale
all'energia cinetica in B ) (trascurando sempre gli attriti).
Dalla formula appena scritta, dividendo ambo i membri per m otteniamo :
e quindi, dividendo ambo i membri per g :
.
Sostituendo i valori numerici e facendo i calcoli otteniamo infine :
.
Da questo risultato appare chiaro che il carrello non riesce a raggiungere il punto C che si trova
alla
quota di 30 m :
07 - Esercizio sulla conservazione dell'energia totale.
Consideriamo un paracadutista di massa m = 80 kg che si lancia da un'altezza h di 2000 m e che
tocca terra alla velocità di v = 3 m/s :
Si chiede a che velocità il paracadutista toccherebbe terra in assenza di aria. Dato poi per scontato
che,
in presenza di aria, egli tocca terra con una velocità inferiore a quella in assenza di aria, si chiede
inoltre
quanta energia meccanica si è perduta (perché trasformata in energia termica assorbita delle
molecole
dell'aria), il lavoro totale fatto dalle forze resistenti (attrito con l'aria) ed il valore medio della forza
d'attrito
(dell'aria).
Soluzione.
Calcoliamo la velocità "teorica" con cui il paracadutista toccherebbe terra se non vi fosse la
resistenza dell'aria.
Poiché, a causa dell'assenza di attriti, tutta l'energia potenziale che il paracadutista ha alla quota
h (si suppone che al momento del lancio la sua velocità sia nulla) si trasforma nell'energia cinetica
che esso avrà al momento di toccare terra (a terra l'energia potenziale è nulla) possiamo scrivere :
cioè :
.
Da questa formula si ricava direttamente v . Per fare questo operiamo le solite semplificazioni
dividendo ambo i membri per m , moltiplicando per 2 ed estraendo la radice quadrata. Otteniamo
allora :
.
Sostituendo i dati numerici abbiamo :
che trasformata in km/h diventa :
.
Si tratta di una velocità considerevole che non permetterebbe la possibilità di alcun lancio !!
L'effetto
dell'aria, invece, dissipa (assorbe) gran parte dell'energia meccanica del paracadutista
permettendogli
di toccare terra con una velocità "accettabile".
Consideriamo ora la caduta "reale" del paracadutista in presenza della resistenza dell'aria.
L'energia meccanica iniziale del paracadutista alla quota h è pari alla sua energia potenziale
gravitazionale (essendo la sua velocità iniziale nulla) :
.
L'energia meccanica finale, al momento in cui tocca terra (dato che la velocità è nota), è :
.
Il paracadutista aveva alla quota h l'energia meccanica di 1568000 J . Giunto a terra egli ha solo
360 J . E' evidente che, per il principio di conservazione dell'energia in tutte le sue forme, la
differenza fra le due energie si è trasformata in un'altra forma di energia non meccanica. La
differenza di energia la ritroviamo trasformata in calore trasmesso alle molecole dell'aria.
Possiamo per questo immaginare che la forza di attrito (resistenza) dell'aria che si oppone alla
caduta del paracadutista ha compiuto, durante la caduta, il lavoro :
.
Possiamo anche calcolare la forza di attrito media (come se agisse in maniera costante, anche
se sappiamo che la forza di attrito dipende da vari fattori ed in particolare dalla velocità del corpo
che cade per cui essa non è certamente costante). Siccome in generale il lavoro è
,
avremo :
da cui, sostituendo i valori numerici, otteniamo :
che rappresenta appunto la forza di attrito media con cui l'aria si oppone al moto.
Si noti che questa forza è circa pari al peso del paracadutista che vale :
.
Questo dipende dal fatto che, a causa dell'attrito dell'aria, dopo poco tempo dal lancio, il
paracadutista
procede di moto rettilineo uniforme perché la forza peso è appunto neutralizzata dalla forza di
attrito
dell'aria. Per gran parte del moto, quindi, la forza di attrito è uguale (in intensità) alla forza peso del
paracadutista.
08 - Esercizio.
Consideriamo la dinamica del giro della morte (trascurando gli attriti).
Un motociclista esegue il giro della morte in modo che, nel punto più alto della traiettoria circolare
che egli compie, la forza centrifuga a cui è soggetto sia esattamente uguale (come intensità,
perché
i versi sono opposti) al suo peso (sommato a quello della motocicletta) (d'ora in poi, per esigenze
di fluidità di scrittura, dicendo "motociclista" consideriamo anche la sua moto, ovvero intenderemo
il sistema motociclista + motocicletta) (per comodità grafica abbiamo indicato il sistema
motociclista +
motocicletta con un tondino nero).
Questa condizione (uguaglianza in intensità fra forza centrifuga e forza peso) fa sì che nel punto
A il motociclista tocchi appena la traiettoria. Questa condizione è necessaria per semplificare i
calcoli che dovremo fare. Nella realtà, la forza centrifuga in A potrebbe benissimo superare in
intensità la forza peso, mentre non dovrebbe mai esserne inferiore, pena la caduta del motociclista.
Abbiamo detto che trascuriamo gli attriti per cui possiamo considerare in via teorica che il sistema
sia già a "regime", ovvero che il motociclista percorra a motore spento ed indefinitamente la
traiettoria.
In realtà il motore acceso della motocicletta fornisce continuamente l'energia perduta a causa degli
attriti facendo sì che il motociclista non si stacchi dalla traiettoria e precipiti a terra.
Nel punto A si deve perciò avere :
dove
sia m .
indica l'intensità della forza centrifuga in A e p il peso del motociclista la cui massa
Ricordando che la forza centrifuga vale
scriveremo allora :
dove
( v è la velocità e R è il raggio del cerchio)
è la velocità del motociclista in A , ovvero, dividendo ambo i membri per m e
moltiplicando per R :
.
Questa formula esprime la velocità al quadrato del motociclista in A in situazione di equilibrio
di forze.
Consideriamo ora il bilancio energetico (trascurando gli attriti).
In B l'energia potenziale gravitazionale del motociclista è nulla mentre in A la sua energia
meccanica
si compone come al solito nella somma fra energia cinetica ed energia potenziale. Avremo allora :
ovvero :
dove 2R è la quota del punto A .
Moltiplicando ambo i membri per 2 otteniamo :
.
Raccogliendo m al secondo membro abbiamo :
da cui, dividendo ambo i membri per m , ricaviamo :
.
Questa formula ci fornisce il valore della velocità al quadrato del motociclista in B .
D'altra parte, in B la forza centrifuga a cui è soggetto il motociclista è :
per cui, sostituendo il valore di
precedentemente trovato, otteniamo :
da cui, sostituendo il valore di
trovato all'inizio, ricaviamo :
.
La formula appena trovata esprime il fatto che il motociclista in B è soggetto ad una forza
centrifuga pari al quintuplo del proprio peso ( mg ) !!!
Sommando in B a questa forza centrifuga anche la forza peso del motociclista (rivolta nello
stesso verso) otteniamo lo "sbalorditivo" risultato che il motociclista in B è soggetto ad una
forza complessiva pari al sestuplo del suo peso :
.
09 - Esercizio.
Calcolare a quale distanza dalla Terra si devono trovare i satelliti geostazionari.
I dati del problema sono :
costante di gravitazione universale :
massa della Terra :
raggio della Terra :
.
Soluzione.
Risolviamo il problema scegliendo un sistema di riferimento inerziale (per esempio il sistema
delle stelle fisse). Riferire il moto dei corpi a sistemi di riferimento inerziali è sempre conveniente
perché se li riferiamo a sistemi di riferimento non inerziali (per esempio ruotanti come la superficie
della terra) occorre introdurre, perché continuino a valere le 3 leggi della dinamica, le cosiddette
forze apparenti con il risultato di "complicare" in generale la risoluzione dei problemi ad essi
connessi.
Il satellite S ruota attorno alla Terra compiendo un'orbita circolare di raggio R rispetto al centro
della medesima. Poiché il satellite è geostazionario (cioè "visto" immobile nel cielo rispetto ad un
osservatore sulla superficie terrestre), il tempo T impiegato da esso a compiere un giro completo
deve essere pari ad un giorno ( 24 ore).
Rispetto al sistema di riferimento inerziale delle stelle fisse, il satellite S , poiché non si muove di
moto
rettilineo uniforme ma si muove di moto circolare uniforme, è soggetto ad una forza centripeta
che
lo mantiene sulla sua traiettoria circolare (ricordiamo che, per il principio d'inerzia, un corpo su
cui
non agiscono forze o su cui la risultante delle forze è nulla permane, rispetto ad un sistema di
riferimento
inerziale, nel suo stato di quiete o di moto rettilineo uniforme finché una forza esterna non
interviene a
modificarne lo stato di moto).
Chiamiamo con
la forza centripeta che costringe il satellite a compiere una traiettoria circolare.
Da cosa è prodotta fisicamente la forza centripeta
gravitazionale
? Essa coincide con la forza di attrazione
con cui la Terra attira a sé il satellite.
Noi conosciamo già le formule che esprimono le intensità delle suddette forze. Esse sono :
e
dove m è la massa del satellite, v è la sua velocità periferica, G è la costante di gravitazione
universale e M è la massa della Terra.
Dovendo le due forze coincidere, potremo scrivere :
ovvero :
.
Vediamo ora di semplificare l'equazione in modo da ricavare il valore di R
Dividendo entrambi i membri per m si ottiene :
.
D'altra parte la velocità periferica v del satellite é
.
Sostituendo tale velocità nella formula precedente otteniamo :
che si semplifica in :
ed in :
.
Moltiplichiamo ora ambo i membri per
:
e semplifichiamo :
.
Moltiplichiamo ambo i membri per
e semplifichiamo :
:
.
Abbiamo così trovato una semplice equazione di terzo grado nell'incognita R . Per risolverla basta
estrarre le radici cubiche di entrambi i membri :
da cui si ottiene :
che rappresenta la soluzione del problema.
Si noti il fatto molto importante che la distanza R con cui ruota un satellite geostazionario non
dipende
dalla massa del medesimo. Questo significa che tutti i satelliti geostazionari, indipendentemente
dalla
loro massa, ruotano alla stessa distanza da terra.
Sostituendo i dati numerici abbiamo :
dove abbiamo posto
.
Si noti che in questi calcoli usiamo, come sempre, le proprietà delle potenze preferendo le potenze
di 10 (per la loro comodità di utilizzo). Si noti anche che le unità di misura delle varie grandezze
in
gioco sono, come sempre, espresse nel Sistema Internazionale (S.I.).
A conti fatti (approssimando), otteniamo il risultato :
.
Per conoscere l'effettiva "quota" h a cui è posto il satellite geostazionario, basta sottrarre da R la
misura r del raggio terrestre, cioè :
h=R-r.
Otteniamo quindi :
che corrisponde ad una quota di circa 36.000 km .
Equazione della parabola in fisica
01 - La parabola in fisica.
Rispetto ad un sistema di riferimento cartesiano ortogonale 0xy , l'equazione di una generica
parabola con asse parallelo all'asse delle y è :
.
In fisica, molte formule hanno forma analoga e quindi corrispondono a delle parabole.
Per esempio, la formula che dà lo spazio in funzione del tempo in un moto uniformemente
accelerato è :
dove
è lo spazio iniziale, ovvero lo spazio al tempo t = 0 ,
è la velocità iniziale,
ovvero la velocità al tempo t = 0 , ed a è l'accelerazione costante a cui è soggetto il corpo.
Dal punto di vista matematico, la formula scritta sopra rappresenta una parabola (dove la
variabile indipendente (la x della formula generale della parabola) è t e la variabile dipendente
(la y della formula generale della parabola) è s ). Graficamente :
Un altro esempio di formula fisica riconducibile alla parabola è :
dove T è l'energia cinetica, m la massa e v la velocità. Naturalmente questa formula
rappresenta una parabola se come variabile indipendente si considera v .
Un altro esempio è :
dove
è la forza centripeta, m la massa, v la velocità e r il raggio della traiettoria.
Vediamo ora alcuni esempi di applicazione della parabola in fisica.
02 - Moto uniformemente accelerato : partenza da fermo.
Immaginiamo che un corpo parta fa fermo con accelerazione a costante. Immaginiamo, per
comodità, di fare partire il cronometro ( t = 0 ) quando il corpo si trova nella posizione s = 0 .
Il moto in questione è uniformemente accelerato e la sua equazione oraria è allora semplicemente :
(essendo
e
entrambi nulli).
L'equazione oraria appena scritta è l'equazione di una parabola (considerando t la variabile
indipendente).
Facciamo il caso concreto di a = 4 m/s² .
L'equazione diventa :
.
Si tratta di una parabola con vertice nell'origine e concavità rivolta verso l'alto (essendo il
coefficiente del termine di secondo grado t² positivo). Disegnamone il grafico partendo dalla
tabella oraria :
ottenuta dando valori di comodo al tempo t .
Il grafico orario è quindi :
03 - Moto uniformemente accelerato : frenata.
Consideriamo un corpo dotato di velocità
che all'istante t = 0 inizia a
frenare con accelerazione costante negativa a = -5 m/s² . Supponiamo che al tempo t = 0
lo spazio sia anch'esso nullo (
= 0 ).
L'equazione oraria del moto sarà allora :
.
Si tratta di una parabola con concavità rivolta verso il basso che passa per l'origine ed ha
vertice V(6,90) (l'abbiamo calcolato usando la nota formula del vertice
Per disegnarla ricaviamo la seguente tabella oraria :
Il grafico è quindi :
).
04 - Energia cinetica.
L'energia cinetica di un corpo di massa m dotato di velocità v è :
.
Se consideriamo come variabile indipendente la velocità v , la funzione qui scritta è rappresentata
da una parabola. Notando che, se la velocità raddoppia, l'energia cinetica diventa quattro volte
maggiore, possiamo tracciare il seguente grafico :
Si noti che qui abbiano usato una scala delle ascisse inusuale ma comoda per "sottolineare"
visivamente
che se la velocità dimezza l'energia diventa un quarto.
Chi guida un autoveicolo dovrebbe "osservare" molto bene questo grafico !!! Egli noterebbe che
per passare da 100 km/h a 50 km/h deve "perdere" i tre quarti dell'energia cinetica che aveva
inizialmente. Anche per passare da 50 km/h a 25 km egli deve perdere i tre quarti dell'energia
cinetica che aveva alla velocità di 50 km/h .
05 - Esercizio.
Un pedone corre alla velocità v = 18 km/h per prendere l'autobus. Quando si trova a 10 m
dall'autobus, questo parte con un moto uniformemente accelerato di accelerazione a = 1 m/s² .
Riuscirà il pedone a salire sull'autobus ?
Soluzione.
Il pedone corre con velocità costante pari a v = 18km/h = 5m/s (moto rettilineo uniforme). Al
tempo t = 0 esso si trova nella posizione s = 0 . L'equazione oraria del suo moto è allora :
s = 5t .
L'autobus, al tempo t = 0 , si trova nella posizione s = 10 m . A quell'istante esso inizia a
muoversi
(partendo da fermo) di moto rettilineo uniformemente accelerato con accelerazione costante
a = 1 m/s² (il moto dell'autobus è nella stessa direzione e verso del moto del pedone). L'equazione
oraria dell'autobus sarà allora :
ovvero, sostituendo i dati noti :
(la velocità iniziale dell'autobus è nulla).
Il moto del pedone è rappresentato nel grafico tempo-spazio da una retta, mentre quello
dell'autobus
da una parabola.
Costruiamo ora la seguente tabella oraria :
t(s) s(pedone)(m) s(autobus)(m)
0
0
10
1
5
10 + 1/2 = 10,5
2
10
10 + 2 = 12
3
15
10 + 9/2 = 14,5
4
20
10 + 8 = 18
5
25
10 + 25/2 = 22,5
6
30
10 + 18 = 28
7
35
10 + 49/2 = 34,5
8
40
10 + 32 = 42
...
...
...
ottenuta sostituendo valori di comodo di t nelle due equazioni orarie.
Come si vede bene, al tempo t = 3 il pedone si trova davanti all'autobus. Questo significa che poco
primo egli lo ha raggiunto. Al tempo t = 8 l'autobus si trova davanti al pedone. L'autobus ha quindi
sorpassato il pedone prima di quell'istante.
Il grafico dei due moti è :
Da esso si deduce che all'istante t = 2,8 circa il pedone ha raggiunto l'autobus ed all'istante t =
7,2
circa l'autobus ha sorpassato il pedone.
La determinazione grafica dei due punti d'incontro dei grafici è verificabile algebricamente
risolvendo
il sistema :
.
In generale, in geometria analitica, risolvere il sistema fra le equazioni di due curve significa
trovare
le coordinate dei punti di incontro delle medesime. Questo dipende dal fatto che le coordinate dei
punti d'incontro di due curve ne soddisfano "contemporaneamente" le equazioni.
Eguagliando i secondi membri delle due equazioni (essendo ovviamente s = s ) si ottiene :
(la barra "/" significa che ripetiamo la prima equazione senza riscriverla).
La seconda equazione diventa (portando tutto al primo membro ed ordinando) :
da cui, moltiplicando ambo i membri per 2 , si ottiene :
.
Risolvendo l'equazione di secondo grado così ottenuta usando la nota formula otteniamo :
.
Negli istanti
verificato
graficamente.
e
così trovati avvengono i due "incontri" fra pedone ed autobus così come
Se la velocità del pedone fosse opportunamente minore del valore v = 5 indicato dal problema (a
parità
del moto dell'autobus), potrebbe succedere che il pedone avrebbe una sola occasione di salire
sull'autobus
o addirittura non ne avrebbe alcuna. Graficamente :
06 - Altra applicazione della parabola in fisica.
Due automobili identiche (auto A ed auto B ) stanno procedendo su di una strada rettilinea alla
velocità costante v = 90 km/h = 25 m/s . Esse sono poste ad una distanza d = 20 m .
Al tempo t = 0 l'automobile B inizia a frenare con accelerazione costante negativa tale per cui
in
essa è completamente ferma. L'automobile A , dopo un tempo di reazione
comincia a frenare allo stesso modo (le due auto sono identiche a tutti gli effetti).
,
L'automobile A tamponerà l'automobile B ?
Innanzi tutto calcoliamo l'accelerazione di frenata. Essa sarà :
.
L'equazione oraria dell'automobile B sarà allora :
(supponendo che al tempo t = 0 l'auto A si trova nella posizione s = 0 ).
Si tratta di una parabola con concavità rivolta verso il basso.
Per disegnarla, possiamo prendere in considerazione la seguente tabella oraria :
auto B
t(s)
s(m)
0
20
1
20 + 25 - 2,5 = 42,5
2
20 + 50 - 10 = 60
3
20 + 75 - 22,5 = 72,5
4
20 + 100 - 40 = 80
5
20 + 125 - 62,5 = 82,5
...
...
L'equazione oraria dell'automobile A è invece composta di due parti :
- 1 - per
oraria :
. In questo intervallo di tempo, il moto è rettilineo uniforme con equazione
s = 25t che rappresenta una retta
e :- 2 - per t > 1 . In questo intervallo di tempo, il moto è rettilineo uniformemente accelerato con
equazione oraria :
.
che rappresenta una parabola con concavità rivolta verso il basso. Il perché della
formula
scritta sopra è evidente considerando che per un eventuale cronometro che segni t = 0
quando l'automobile A inizia a frenare l'equazione oraria di A sarebbe :
,
essendo lo spazio iniziale 25 m , la velocità iniziale 25 m/s e l'accelerazione -5 m/s² .
Ma il tempo lo misuriamo quando B inizia a frenare, per cui al posto di t dobbiamo
porre t - 1 .
Disegnando i grafici delle curve otteniamo :
da cui si deduce che l'automobile A tampona B poco prima che l'auto B sia completamente
ferma.
Per evitare l'urto (a parità di velocità) basterebbe aumentare la distanza di sicurezza fra le auto ...












