Introduzione alla Statistica e al Calcolo delle Probabilità – M
Prova Scritta
25 Giugno 2009
Esercizio 1
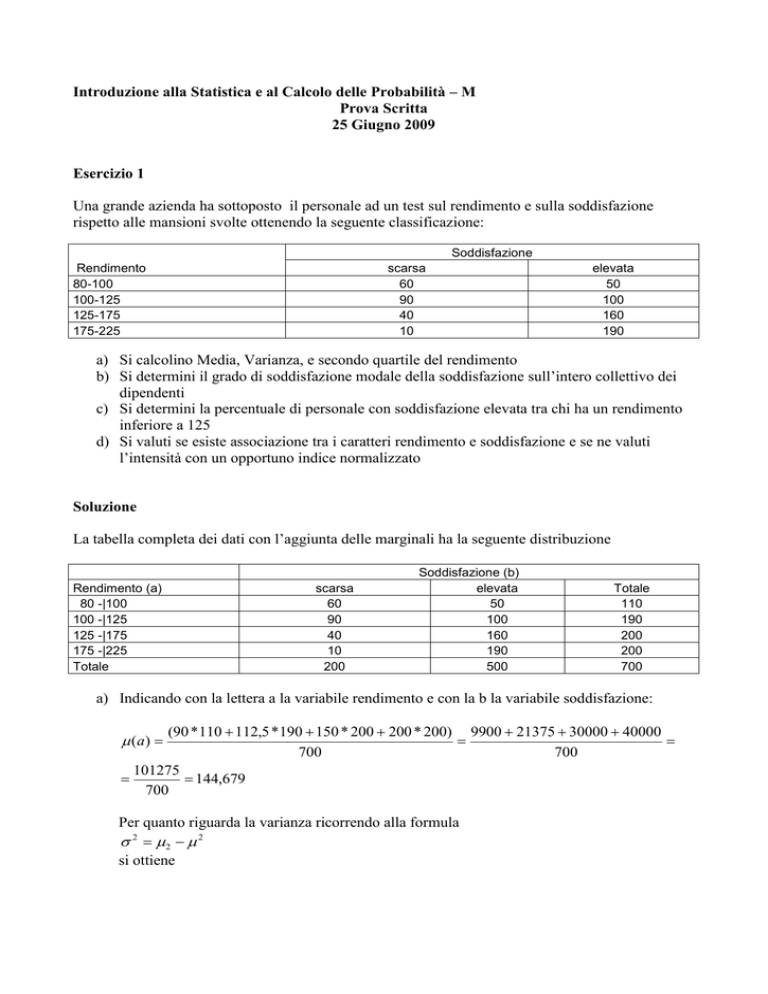
Una grande azienda ha sottoposto il personale ad un test sul rendimento e sulla soddisfazione
rispetto alle mansioni svolte ottenendo la seguente classificazione:
Soddisfazione
Rendimento
80-100
100-125
125-175
175-225
scarsa
60
90
40
10
elevata
50
100
160
190
a) Si calcolino Media, Varianza, e secondo quartile del rendimento
b) Si determini il grado di soddisfazione modale della soddisfazione sull’intero collettivo dei
dipendenti
c) Si determini la percentuale di personale con soddisfazione elevata tra chi ha un rendimento
inferiore a 125
d) Si valuti se esiste associazione tra i caratteri rendimento e soddisfazione e se ne valuti
l’intensità con un opportuno indice normalizzato
Soluzione
La tabella completa dei dati con l’aggiunta delle marginali ha la seguente distribuzione
Rendimento (a)
80 -|100
100 -|125
125 -|175
175 -|225
Totale
scarsa
60
90
40
10
200
Soddisfazione (b)
elevata
50
100
160
190
500
Totale
110
190
200
200
700
a) Indicando con la lettera a la variabile rendimento e con la b la variabile soddisfazione:
(90 * 110 112,5 * 190 150 * 200 200 * 200) 9900 21375 30000 40000
700
700
101275
144,679
700
(a)
Per quanto riguarda la varianza ricorrendo alla formula
2 2 2
si ottiene
2
(90 2 *110 112,5 2 *190 150 2 * 200 200 2 * 200
700
15795688
22565,27
700
da cui:
2 22565,27 (144,679) 2 1633,379
Il secondo quartine corrisponde al valore mediano x a , 0 ,5 . Per calcolarlo, poiché N=700 è pari
occorre individuare in quale classe cadono le unità 350 e 351
Unità
110
190
200
200
700
80 -|100
100 -|125
125-| 175
175-| 225
Totale
da
0
111
301
501
a
110
300
500
700
La classe mediana è la 125-| 175
xa ,0.5 xi* [( N / 2) Fi*1 ]
di
50
=112,5
125 350 300
200
fi
b) Il grado di soddisfazione modale è “elevata” che corrisponde al 71,4% delle unità
c) La percentuale di dipendenti molto soddisfatti tra quelli con rendimento inferiore a 125 è
pari al 50%
50 100
0,5
110 190
d) Per valutare se esiste associazione tra i caratteri rendimento e soddisfazione si costruiscono
le frequenze teoriche che si avrebbero sotto l’ipotesi di indipendenza f i*,j .
Frequenze teoriche
Rendimento
80-100
100-125
125-175
175-225
Totale
scarsa
31,429
54,286
57,143
57,143
200
elevata
78,571
54,286
142,857
142,857
500
Totale
110
190
200
200
700
Poiché queste sono diverse da quelle reali e quindi esiste una qualche associazione tra i caratteri
si utilizza l’indice 2 per valutarne l’intensità.
L’indice chi-quadrato è dato da
2
(f
i
j
ij
f ij* ) 2
f ij*
(60 31,429) 2
(190 142,857) 2
....
31,429
142,857
=25,974+10,39+23,496+9,398+130,908+5,143++2,057+38,893+15,557=130,908
2
Alternativamente è possibile usare la formula:
2
f ij
N i j
1 =
f i. * f . j
=700*(0,164+0,045+0,213+0,105+0,04+0,256+0,003+0,261-1)= 130,908
2
Per valutare l’intensità dell’associazione è necessario relativizzare l’indice. A tal fine si utilizza
il coefficiente di Cramer
V
2
N (min( k 1)( h 1)
=
130,908
=0,432
700 *1
che indica un livello di associazione pari al 43% del livello massimo.
=
Esercizio 2
In un’urna contiene monete in centesimi di euro (tipo 1) e in centesimi di dollaro (tipo 2).
Siano:
- p1 0,6 la probabilità di ottenere una croce lanciando una moneta di tipo 1
- p2 0,5 la probabilità di ottenere una croce lanciando una moneta di tipo 2.
- k1 0,4 la probabilità di estrarre dall’urna una moneta di tipo 1.
Si estrae una moneta a caso e la si lancia.
Calcolare la probabilità che:
a) esca croce
b) sia stata scelta una moneta di tipo 1 sapendo che è uscita testa
Supponiamo che p1 p2 p
c) dimostrare che in questo caso gli eventi E1 estrazione di una moneta di tipo 1 e C uscita di
una croce sono indipendenti cioè che P( E1 | C) P( E1 )
(Suggerimento: utilizzare le formule nella forma della sola notazione teorica)
Soluzione
Si definisce la notazione:
-
C evento uscita di una croce
P(C) probabilità dell’ evento uscita di una croce
Ei estrazione di un tipo di moneta i con i=1,2
K1=P(E1) probabilità dell’ evento estrazione di una moneta di tipo 1
a) Per ottenere P(C) si utilizza la formula:
2
P(C ) i 1 P(C | Ei ) P( Ei ) P(C | E1 ) P( E1 ) P(C | E 2 ) P( E 2 )
p1 k1 p 2 (1 k1 ) 0,6 * 0,4 0,5 * (1 0,4) 0,54
b) Per il teorema di Bayes
P(T | E1 ) P( E1 )
(1 p1 )k1
0,4 * 0,4
P( E1 | T )
0,348
P(T )
(1 p1 )k1 (1 p2 )(1 k1 ) 0,4 * 0,4 0,5 * 0,6
c) Questo segue immediatamente inserendo p p1 p2 nella formula
P(C | E1 ) P( E1 )
P( E1 | C )
P(T )
Infatti:
P(C | E1 ) P( E1 )
pk1
k1
P( E1 | C )
=
k1 P( E1 )
P(T )
pk1 p(1 k1 ) k1 (1 k1 )
Poiché P(T ) 0
Si ha P( E1 C) P( E1 ) P(T ) P( E1 | C) P( E1 )
Esercizio 3
La produzione dei filari di un frutteto di mele è interpretata da una vc X normale con media 1000 kg
e varianza 40.000.
Si calcoli
a) La probabilità che un filare produca esattamente 100 kg di mele
b) La probabilità che un filare produca meno di 500 kg di mele
c) La probabilità che un filare produca tra gli 800 e i 1100 kg di mele
d) Supponendo che la media sia ignota, che valore dovrebbe assumere affinché la probabilità
che un filare produca meno di 500 kg di mele sia 0,6915?
Svolgimento
La variabile casuale in esame è quindi X N (1000; 200)
a) La probabilità che una v.c. normale assuma un valore puntuale è pari a 0, qualunque sia il
valore. Questo permette di assimilare qualunque probabilità che implichi e alla
maggiorazione e minorazione strette.
b) Per calcolare questa probabilità occorre ricondurre la v.c. X ad una normale standardizzata Z
ed ottenere il valore della Z che corrisponde al valore X=500
X 500 1000
500
2,5
200
40000
Utilizzando le tavole si ottiene che
P( Z 2,5) 1 P( Z 2,5) 1 0,9938 0,0062
c) La probabilità che un filare produca tra gli 800 e 1100 chili si ottiene analogamente al caso
precedente
1100 1000
800 1000
P(800 X 1100) P
Z
P 1 Z 0,5
200
200
P( Z 0,5) P( Z 1) 0,6915 1 PZ 1 0,6915 1 0,8413 0,5328
d) In questo caso la media è ignota ma è noto che
500
P( X 500) P Z
0,6915
200
500
0,5
da qui otteniamo che
200
quindi il valore della media è 500 0,5 * 200 da cui 400












