Sistema di comunicazione
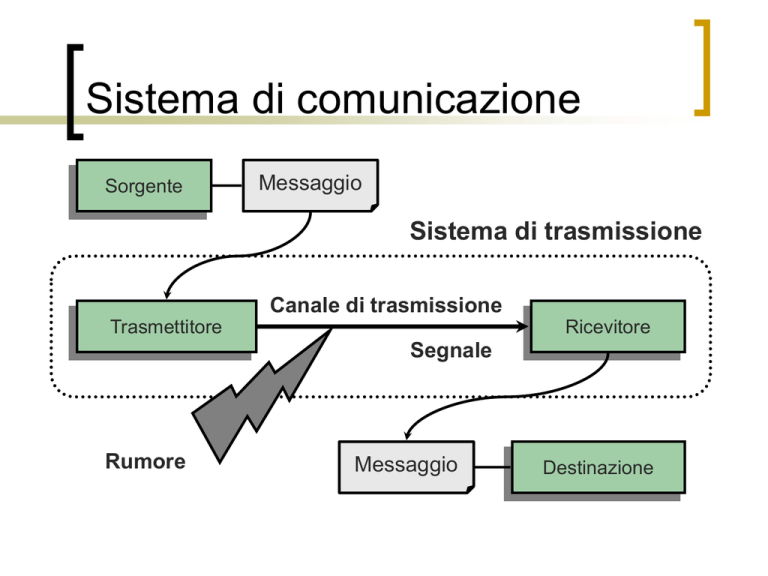
Sorgente
Messaggio
Sistema di trasmissione
Canale di trasmissione
Trasmettitore
Ricevitore
Segnale
Rumore
Messaggio
Destinazione
Sistema di comunicazione
A causa del rumore, non è sempre possibile
garantire che i dati ricevuti da un canale di
trasmissione siano corretti.
Si verifica un errore di trasmissione
quando il dato ricevuto in uscita dal canale è
diverso dal dato immesso.
L’errore si definisce singolo, doppio, triplo ecc. in
base al numero di bit errati.
Esistono appositi codici di rilevazione e
correzione degli errori di trasmissione.
Sistema di comunicazione
Codice di parità: al dato da trasmettere si
aggiunge un bit di parità, che indica se gli 1
del dato sono pari o dispari.
parità pari: es. a 01001110 si aggiunge 0 per
ottenere 01001110 0
parità dispari: es. a 01101110 si aggiunge 1 per
ottenere 01001110 1
I dati ricevuti devono avere sempre un
numero pari di 1, altrimenti sono errati.
Permette di rilevare solo gli errori singoli o
dispari.
Sistema di comunicazione
Esempio.
C
I
A
100 0011 100 1001 100 0010
Messaggio
Usando la parità pari, viene inviato
100 1111
C
O
I
A
1100 0011 1100 1001 0100 0010
Se arriva
C
Y
1100 1111
A
1100 0011 1101 1001 0100 0010
O
/
1010 1111
Viene rilevato solo l’errore nel secondo
carattere
Sistema di comunicazione
Parità incrociata:
Oltre alla parità sul singolo
carattere, viene aggiunto un
byte al termine di un
pacchetto di lunghezza
fissata.
Ogni bit della codifica
aggiunta è calcolato con il
controllo di parità su tutti i bit
della colonna che lo
sovrasta.
C
1
100 0011
I
1
100 1001
A
0
100 0010
O
1
100 1111
1
000 0111
Sistema di comunicazione
Parità incrociata:
Se un solo bit viene
alterato, il ricevitore è in
grado di rilevarlo e
correggerlo.
Se due o più bit vengono
modificati, il ricevitore può
rilevarli e/o correggerli in
funzione della loro
posizione
C
1
100 0011
I
1
101 1001
A
0
100 0010
O
1
100 1111
1
000 0111
C
1
100 0011
Y
1
101 1001
A
0
100 0010
/
1
010 1111
1
000 0111
Sistema di comunicazione
Codici CRC (Cyclic Redundancy Checking)
I bit da inviare sono considerati come i coefficienti di
un polinomio P(x) da dividere per un polinomio S(x),
detto polinomio generatore, noto al trasmettitore e al
ricevitore.
Al messaggio originario viene accodato il resto R(x)
che prende il nome di CRC.
Il ricevitore esegue la divisione dei dati ricevuti per
S(x) e verifica la correttezza dei dati pervenuti
Scegliendo opportunamente il polinomio generatore,
il metodo risulta molto affidabile, poiché solo i rumori
che creano un errore esattamente multiplo di S(x)
non vengono filtrati.
Sistema di comunicazione
Codici CRC (Cyclic Redundancy Checking)
Esempio:
Messaggio P(x) : 1010 0011
(x7+x5+x+1)
Polinomio generatore S(x) : 1001 (x3+1)
Resto della divisione R(x) : 101 (x2+1)
Da inviare 1010 0011 101
Se viene ricevuto come 1010 0101 101
ripetendo la divisione di 1010 0101 per S(x) si
ottiene come resto 011 (≠ 101) che denota la
presenza di una configurazione errata.
Sistema di comunicazione
Metodo di Hamming (1950)
Codice a correzione d’errore
Codice ridondante, ovvero utilizza un
numero maggiore di bit rispetto al
numero strettamente necessario
Consente di correggere 1 singolo
errore
Sistema di comunicazione
Metodo di Hamming
Aggiunge un numero r
di bit di controllo pari al
limite teorico inferiore
(m+1≤2r-r) dove m è la
dimensione del
messaggio.
m
r
tot.
% r/tot
1
2
3
67%
2
3
5
60%
3
3
6
50%
4
3
7
43%
5
4
9
44%
6
4
10
40%
7
4
11
36%
8
4
12
33%
9
4
13
31%
10
4
14
29%
11
4
15
27%
Sistema di comunicazione
Metodo di Hamming
I bit di controllo sono inseriti nelle posizioni
aventi come indice 2k una potenza di due (1,
2, 4, 8, 16, . . . )
I bit del messaggio sono inseriti nelle altre
posizioni della parola di codice
Il bit di controllo in posizione 2k assume
valore in modo da controllare la parità pari di
tutti quei bit le cui posizioni contengono 1 nel
bit k-esimo della scomposizione in binario.
Sistema di comunicazione
Metodo di Hamming
Per codificare il byte 0111 1001 con m=8 si
aggiungono r=4 bit di controllo(nelle posizioni
1,2, 4 e 8) per un totale di 12 bit:
Il bit di controllo in posizione 1= 20 controlla
le posizioni 1, 3, 5, 7, 9,11
Il bit di controllo in posizione 2= 21 controlla
le posizioni 2, 3, 6, 7, 10, 11
Il bit di controllo in posizione 4=22 controlla le
posizioni 4, 5, 6, 7, 12
Il bit di controllo in posizione 8= 23 controlla
le posizioni 8, 9, 10, 11, 12
Sistema di comunicazione
Metodo di Hamming
Bit 1 >> 1, 3, 5, 7, 9,11
Bit 2 >> 2, 3, 6, 7, 10, 11
Bit 4 >> 4, 5, 6, 7, 12
Bit 8 >> 8, 9, 10, 11, 12
8
4
2
1
0
0
0
0
0
1
0
0
0
1
2
0
0
1
0
3
0
0
1
1
4
0
1
0
0
5
0
1
0
1
6
0
1
1
0
7
0
1
1
1
8
1
0
0
0
9
1
0
0
1
10
1
0
1
0
11
1
0
1
1
12
1
1
0
0
Sistema di comunicazione
Metodo di Hamming
In trasmissione:
Posizione
12 11 10
9
Bit originali
0
1
1
8
7
6
5
4
3
1
1
0
0
1
1
1
0
1
2
1
Bit di controllo
1, 3, 5, 7, 9, 11
1
2, 3, 6, 7, 10, 11
1
1
4, 5, 6, 7, 12
0
8, 9, 10, 11, 12
0
1
1
1
1
Da inviare
0
1
1
1
1
1
0
1
0
0
1
1
0
0
1
0
1
0
1
0
0
Sistema di comunicazione
Metodo di Hamming
In ricezione, supponendo che il bit in posizione
9 sia stato commutato, i bit di controllo 1 e 8
segnalano l’errore in posizione 1+8=9
permettendone la correzione
Posizione
Ricevuti
12 11 10
9
8
7
6
5
4
3
2
1
0
0
1
1
0
0
1
1
0
0
1
1
Parità
Bit di controllo
1, 3, 5, 7, 9, 11
1
2, 3, 6, 7, 10, 11
1
4, 5, 6, 7, 12
0
8, 9, 10, 11, 12
0
1
0
1
1
1
0
1
0
1
0
1
0
1
1
0
1
0
0
NO
OK
OK
NO










