fibre ottiche

CORSO DI SISTEMI DI TELECOMUNICAZIONE
ANNO ACCADEMICO 2009-2010
COLLEGAMENTI IN FIBRA OTTICA
Prof. Carlo Regazzoni
D.I.B.E.-Università di Genova
1
RIFERIMENTI BIBLIOGRAFICI
[1]
P. Mandarini, “Comunicazioni Elettriche”, Vol. I
e II, Editrice Ingegneria 2000, Roma: 1989.
[2]
M. Luise, “Sistemi di Trasmissione su fibra
ottica”, Edizioni ETS, Pisa: 1996.
[3]
G. Bonaventura, “Verso una rete tutta ottica”,
Mondo Digitale, anno IV n.3, settembre 2005,
pp. 32-43
D.I.B.E.-Università di Genova
2
PARTE PRIMA:
GENERALITA’ SULLA TRASMISSIONE A
FIBRA OTTICA
D.I.B.E.-Università di Genova
3
FIBRE OTTICHE: GENERALITA’
La trasmissione di segnali elettrici mediante fibre ottiche è
realizzabile applicando ad un estremo della fibra una sorgente di
luce (infrarosso: 0.52.0m di lunghezza d’onda) in grado di
variare la potenza istantanea di emissione proporzionalmente al
segnale da trasmettere, e collegando l’altro estremo della fibra
ad un fotodiodo, in grado di generare una corrente proporzionale
alla potenza luminosa (istantanea) ricevuta.
i(t)=k’WR(t)
Fibra ottica
s(t)
Sorgente
Fotodiodo
WT(t)=ks(t)
R
WR(t)
D.I.B.E.-Università di Genova
4
Note Storiche sulle Fibre Ottiche
• 1500 : Murano(Venezia) utilizzo della propagazione guidata
della luce nel vetro per fini artistici
•1950 : Van Heel,Hopkins e Kanapy della Corning Glass (U.S.A)
sviluppano il fiberscope per usi medicali; Kanapy introduce in
letteratura il termine fibra ottica
•1960 : sviluppo delle sorgenti ottiche LED e LASER
•1970 : Corning Glass commercializza le prime fibre ottiche stepindex multimodo , attenuazione  20dB/km
•1980 : uso massivo delle comunicazioni ottiche
D.I.B.E.-Università di Genova
5
Canale di comunicazione in Fibra Ottica
-Propagazione guidata ,segnale ottico, trasmissione digitale-
Caratteristiche fondamentali
trasmissione in fibra ottica
di
una
•Mezzo di trasmissione: fibra in vetro-silice
plastica(tipo nylon)
linea
di
o fibra di
•Diametro fibra  125 micron (standard)
•Attenuazione  0.2 -5 dB/km ( fibra in vetro-silice monomultinodo) indipendente dalla frequenza di modulazione;
elevata distanza fra amplificatori di linea per rigenerare il
segnale (> 100km per fibre in vetro-silice monomodo).
D.I.B.E.-Università di Genova
6
a) Vantaggi:
•
Elevata capacità di trasmissione ( alcune decine di Gbit/s);
•
Immunità da interferenze elettromagnetiche;
•
Elevata sicurezza dei dati trasmessi (bassa probabilità di
intercettazione).
b)
Svantaggi:
•Trasmissione di informazioni (segnali ottici), non di potenza.
•Gli amplificatori di linea dovrebbero essere alimentati tramite
linea di alimentazione (ottica o elettrica) separata dalla fibra
ottica di comunicazione, oppure tramite batteria.
D.I.B.E.-Università di Genova
7
Comunicazione in Fibra Ottica
-Onde el.m. nelle T.L.C.-
108
10 11
1015
VLF
VHF
EHF
ottica
Telefonia
radar
radio,tv
1020
f[Hz]
raggi X
Rosso
arancio
giallo
verde
blu
violetto
103
Segnale
ottico
Infrarosso (I.R.)
c/f[10-6m=m]
f[1015Hz]
visibile
D.I.B.E.-Università di Genova
UltraVioletto(U.V.)
8
Efficienza di una linea in fibra ottica
•Un parametro di efficienza globale di una linea di trasmissione è
dato dal prodotto tra la velocità massima di trasmissione ottenibile
su un dato canale B, utilizzando una data tecnica di modulazione e la
massima distanza L che è possibile coprire a tale velocità:
  BL
Grafico di  al
variare delle
tecnologie
D.I.B.E.-Università di Genova
9
Banda a disposizione in una linea a fibra ottica
•La banda a disposizione in una fibra ottica è dell’ordine di alcuni
terahertz (ovvero 1012 Hz), circa dieci volte superiore a quella
disponibile nelle comunicazioni radio.
•Questa grande disponibilità di banda consente di trasmettere ad
altissima velocità e questo giustifica il grafico riportato nella slide
precedente (in teoria è possibile arrivare a trasmettere ad un rate pari
ad alcuni Tb/s).
•La trasmissione su collegamento hertziano subisce minori
attenuazioni rispetto alla trasmissione su fibra ottica per lunghe
distanze (e quindi si può trasmettere al rate atteso a maggiore
distanza), ma la velocità consentita su fibra è così elevata da far sì
che il prodotto  sia considerevolmente più elevato.
D.I.B.E.-Università di Genova
10
Schema generale di un sistema di trasmissione
numerica su fibra
•La modulazione-dati è impressa con la tecnica On-Off-Keying (OOK),
ovvero presenza/assenza di segnale in uscita dal modulatore, a
seconda che venga trasmesso un bit a “1” o un bit a “0”.
•La sorgente luminosa è in questo caso un diodo LASER, che viene
acceso alla massima potenza, oppure spento.
D.I.B.E.-Università di Genova
11
Schema generale di un sistema di trasmissione
numerica su fibra (continuazione)
•Il segnale ottico prodotto dal LASER ad una certa lunghezza d’onda 0
viene quindi accoppiato alla fibra ottica. La fibra si comporta come una
guida d’onda ottica.
•Il segnale trasmesso viene quindi raccolto dall’estremità terminale
della fibra da un dispositivo detto fotorivelatore, che è un altro diodo a
semiconduttore, il quale restituisce una corrente elettrica proporzionale
all’intensità del segnale luminoso ricevuto.
•Il segnale viene poi amplificato, integrato (onde eliminare i disturbi
indotti dal processo di fotorivelazione) ed infine rigenerato da un
sogliatore (hard limiter), che restituisce il segnale trasmesso.
•Questo tipo di sistema è detto a rivelazione diretta e costituisce lo
schema-base della quasi totalità dei sistemi di trasmissione in fibra
attualmente in esercizio.
D.I.B.E.-Università di Genova
12
Generazione di sistemi ottici di trasmissione
•La prima generazione di sistemi ottici (fine anni ‘70) faceva uso di
componenti optoelettronici in GaAs (Arseniuro di Gallio), che
funzionavano alla lunghezza d’onda di 0.85m (prima finestra) e di
fibre ottiche di tipo multimodo, ossia in grado di far transitare il
segnale secondo diverse modalità di propagazione.
•La seconda generazione di sistemi ottici (anni ‘80) è caratterizzata da
una lunghezza d’onda di 1.3m (II finestra) e da fibre il cui modo di
propagazione è unico (fibre monomodo).
•La terza generazione di sistemi ottici (anni ‘90) utilizza la zona di
funzionamento della fibra ottica a minima attenuazione (III finestra, 0
= 1.55m per un’attenuazione di 0.25dB/Km).
D.I.B.E.-Università di Genova
13
•La quarta generazione di sistemi ottici (attualmente in uso) mira ad
incrementare la capacità aumentando la sensibilità dei ricevitori
attraverso diverse tecniche di rivelazione del segnale (sistemi
coerenti, o sistemi con amplificatore ottico).
•I sistemi futuri di quinta generazione (sistemi solitonici) si avvarranno
delle proprietà di propagazione non lineare del segnale ottico per
controbattere la distorsione cromatica ed aumentare la banda utile di
trasmissione.
Finestre di funzionamento
dei sistemi di trasmissione
su fibra
D.I.B.E.-Università di Genova
14
PARTE SECONDA:
CARATTERISTICHE TRASMISSIVE
DELLE FIBRE OTTICHE
D.I.B.E.-Università di Genova
15
Segnale Ottico
a) monocromatico
distribuzione spettrale :
() 0(0) =c/f
potenza ottica :
()[W/m]
P   ( )d
0
b)policromatico
distribuzione spettrale
()
potenza ottica :
P   ( )d
[m]
()
0
[m]

D.I.B.E.-Università di Genova
16
Riflessione e rifrazione in una fibra ottica
•Una fibra ottica è sostanzialmente una guida d’onda di materiale
vetroso, il cui fenomeno di guida avviene sulla base di variazioni
dell’indice di rifrazione all’interno del materiale.
•Queste variazioni provocano riflessioni e rifrazioni del segnale ottico
trasmesso, che ne determinano la propagazione.
•I fenomeni di propagazione del segnale su fibra ottica possono essere
studiati mediante due approcci differenti:
•Approccio basato sull’ottica geometrica (semplificato);
•Approccio basato sulle equazioni di Maxwell (formale).
Vedremo, in seguito, sotto quali condizioni i due approcci sopra elencati
possono efficacemente descrivere i fenomeni di propagazione del
segnale ottico.
D.I.B.E.-Università di Genova
17
Parametri caratteristici dell’ottica geometrica
Indice di
rifrazione
c
n ˆ  1
v
•c = velocità di propagazione del
raggio luminoso nel vuoto
u = velocità di propagazione del
raggio luminoso nel mezzo
L’indice di rifrazione è un parametro caratteristico del
mezzo di propagazione del segnale ottico.
Esempi : aria n  1
acqua n  1.3
vetro-silice n  1
cristallo n  1
diamante n  1
D.I.B.E.-Università di Genova
18
Riflessione e rifrazione di un raggio luminoso
Nel caso in cui un raggio luminoso a si trova ad attraversare una supeficie
di interfaccia tra due mezzi con una brusca variazione dell’indice di
rifrazione (es vetro-aria), si ha la situazione schematizzata nella figura
sottostante:
a = raggio incidente
a’ = raggio riflesso nel mezzo 1
b = raggio rifratto (trasmesso)
nel mezzo 2
1 = angolo di incidenza
2 angolo di rifrazione
Legge di
n1sin1  n2 sin 2
Snell
sin1 / sin 2  n2 / n1
D.I.B.E.-Università di Genova
19
Riflessione e rifrazione di un raggio luminoso
•Riferendosi all’esempio della slide precedente, dove n2<n1, si può
osservare che il raggio rifratto tende ad allontanarsi dalla normale, poiché:
sin1 / sin 2  n2 / n1  1 e quindi: sin 2  sin1
 2  1
•Aumentando l’angolo di incidenza, si dovrebbe arrivare ad una situazione
in cui  2   2
•In questo caso, il raggio rifratto non si produce e si ha il fenomeno
della riflessione totale;
•L’angolo di incidenza (detto angolo critico) oltre il quale si ha il
fenomeno della riflessione totale è quello per cui:
 c  arcsinn2 n1 
D.I.B.E.-Università di Genova
20
Applicazione dei concetti teorici su riflessione e
rifrazione del raggio luminoso alla trasmissione ottica
•Dai concetti teorici precedentemente espressi, si può intuire
grossolanamente il principio di funzionamento della guida d’onda in fibra
ottica.
•I raggi in fibra che incidono sull’interfaccia vetro-aria (mezzo 1: vetro,
mezzo 2: aria) con un angolo maggiore di c sono riflessi totalmente e
restano confinati indefinitamente all’interno della fibra stessa, così
come schematizzato nella figura sottostante:
D.I.B.E.-Università di Genova
21
Fibre Ottiche a riflessione totale
•Molti tipi di fibra ottica di utilizzo commerciale non si discostano di molto
dal principio di funzionamento ideale precedentemente menzionato.
•La realizzazione pratica di tali fibre prevede il controllo degli indici di
rifrazione di entrambi i mezzi coinvolti nel fenomeno della riflessione
totale, quindi uno dei due mezzi non può essere l’aria (come ipotizzato in
precedenza per il mezzo 2).
•Nella realtà le fibre a riflessione totale sono costituite da un cilindro
interno, detto nucleo (core), che corrisponde al materiale 1 dell’esempio
precedente ed un guscio cilindrico esterno di materiale vetroso, detto
mantello (cladding), che corrisponde al materiale 2.
•In generale sia il mantello che il nucleo sono costituiti da materiali
vetrosi a diverso indice di rifrazione, ma non mancano fibre in materiale
plastico, dai costi ridotti, ma con caratteristiche di propagazione peggiori
rispetto alle fibre in vetro.
D.I.B.E.-Università di Genova
22
Fibra Ottica a riflessione totale
-Strutturaa)sezione trasversale
b)sezione longitudinale
Cladding (mantello) n2
Core (nucleo) n1>n2
Diametro mantello
125m
Diametro nucleo 50m
D.I.B.E.-Università di Genova
23
Fibre Step-Index
•Le fibre step-index sono caratterizzate da una discontinuità a
gradino dell’indice di rifrazione tra nucleo e mantello.
•E’ possibile studiare le proprietà di propagazione del segnale
mediante le regole dell’ottica geometrica, solo per le fibre stepindex a nucleo largo, ovvero caratterizzate da un raggio del
nucleo molto maggiore della lunghezza d’onda del segnale
luminoso (cioè <<50m).
•La fibra step-index a nucleo largo è il tipo di fibra più semplice da
realizzare, ma presenta, come vedremo, alcuni inconvenienti che la
rendono poco adatta alle applicazioni pratiche.
D.I.B.E.-Università di Genova
24
Fibre Step-Index: analisi della propagazione secondo i
principi dell’ottica geometrica
•Consideriamo una fibra step-index a nucleo largo ed esaminiamo, secondo
i principi dell’ottica geometrica, la propagazione di un raggio
meridionale (ovvero giacente su di un piano passante per l’asse della fibra
stessa).
•Consideriamo un raggio proveniente da una sorgente di segnale, che incide
l’interfaccia nucleo-mantello con un angolo inferiore a c. Tale raggio sarà
parzialmente rifratto nel mantello e la porzione riflessa, a sua volta rifratta,
fino a che il raggio non si esaurisce dopo poche riflessioni interne successive
•In questo caso si dice che il raggio non viene accettato dalla fibra.
D.I.B.E.-Università di Genova
25
Fibre Step-Index: analisi della propagazione secondo i
principi dell’ottica geometrica
Angolo di accettazione della fibra ottica
•Si definisce pertanto un cono di accettazione della fibra, che contiene
tutti i raggi che riescono a propagarsi per riflessione totale del nucleo.
•Il vertice del cono di accettazione giace su un diametro della sezione del
nucleo (vedi figura sottostante) e l’angolo al vertice qa è detto angolo di
accettazione della fibra ottica.
D.I.B.E.-Università di Genova
26
Fibre Step-Index: analisi della propagazione secondo i
principi dell’ottica geometrica
Relazione tra angolo di accettazione ed indici di rifrazione (1)
•Consideriamo un raggio che subisce una riflessione interna totale
(ovvero 1 > c).
•Riferendosi alla figura della slide precedente, l’angolo q1 (complementare
di 1) è l’angolo sotto cui viene rifratto un raggio meridionale entrato in
fibra, e che forma con la medesima un angolo q tale che:
n0 sinq  n1sinq1
n1
sinq 
sinq1
n0
•n0 è l’indice di rifrazione del mezzo esterno alla fibra (aria), che è circa
uguale ad 1. Poichè q1 è complementare di 1 si avrà che:
sinq  n1 cos1
D.I.B.E.-Università di Genova
27
Fibre Step-Index: analisi della propagazione secondo i
principi dell’ottica geometrica
Relazione tra angolo di accettazione ed indici di rifrazione (2)
•Poiché deve essere 1 > c (condizione di riflessione totale), si ha che:
cos1  cos c
•da questo consegue che:
sinq  n1 cos1  n1 cos c  n1 1  sin 2 c  n12  n22
•da cui:
q  arcsin n12  n22  ˆ q a


•Quindi i raggi che si presentano alla bocca della fibra con un angolo q
minore di qa, definito sopra, subiranno una riflessione totale da parte
della fibra e si propagheranno attraverso la fibra stessa. Altrimenti non
saranno accettati dalla fibra e verranno “dispersi” nel mantello.
D.I.B.E.-Università di Genova
28
Fibre Step-Index: analisi della propagazione secondo i
principi dell’ottica geometrica
Apertura numerica di una fibra ottica
•Sovente, invece di qa viene fornito il valore del suo seno, valore che è
chiamato apertura numerica NA (o semplicemente apertura) ovvero:
NA  sinq a  n12  n22
•Tanto maggiore è l’apertura numerica della fibra, tanto più ampio è il
cono di accettazione dei raggi. Con i valori tipici delle fibre per
telecomunicazioni, ovvero n1 = 1.50 ed n2 = 1.47 si ottiene:
NA  0.3
q a  17
D.I.B.E.-Università di Genova
29
Esempio di core e cladding in vetro : n0 = n2  1.50; n1  1.48
Cladding n1
qm
90°-c
c
Asse ottico
Core n2
Mezzo n0< n2
2
2
Angolo di accettazione : qm = arcsin ( n 2  n 1 / n0 )
Apertura numerica : N.A. = n0sin qa =
n 2 2  n 21
Esempio aria/core e cladding in vetro : n0 1 ; n2 1.50 ; n1 1.48 .
N.A. =
n 2 2  n 21
=
(1.50) 2  (1.48) 2
 0.24
qa = arcsin 0.24  14°
m
D.I.B.E.-Università di Genova
30
Esercizio 1
Progettare una fibra ottica con core in vetro (n2 = 1.48) ed angolo
di accettazione qm= 20 ° rispetto ad una sorgente ottica operante in
aria (n01)
aria
qm
Cladding n1 = ?
c
Asse ottico
Core n2 = 0.48
Mezzo n0 1
Soluzione :
occore utilizzare un cladding con indice di rifrazione n21.44
D.I.B.E.-Università di Genova
31
La Dispersione Intermodale nelle fibre Step-Index a
nucleo largo
•La dispersione intermodale è l’inconveniente delle fibre stepindex a nucleo largo.
•Supponiamo di avere due raggi meridionali incidenti sulla bocca
della fibra, uno con l’angolo di incidenza minimo (q = 0) e l’altro
massimo (q = qa), come indicato nella figura sottostante.
D.I.B.E.-Università di Genova
32
La Dispersione Intermodale nelle fibre Step-Index a
nucleo largo
•I due raggi viaggiano all’interno del nucleo alla stessa velocità di
propagazione v = c/n1, ma coprono una stessa distanza L, misurata lungo
l’asse della fibra, attraverso due percorsi diversi, che hanno lunghezza
totale diversa.
•In particolare, il raggio 1 percorre una traiettoria di lunghezza d1 = L,
mentre la traiettoria del raggio 2 è lunga d2 = (L / sin c). Se i due raggi
sono entrati in fibra allo stesso istante, giungono al punto a distanza L sulla
fibra negli istanti:
L
t1 
v
L
t2 
vsin c
•L’intervallo di tempo che intercorre tra i due istanti è pari a:
 ˆ 1 
n2
n1
 Ln1  n1
 Ln12
L 1
  1 
t  t 2  t1  
 1 

v  sin c
c  n2  cn2

Variazione relativa
dell’indice di
rifrazione
D.I.B.E.-Università di Genova
33
La Dispersione Intermodale nelle fibre Step-Index a
nucleo largo
•Questo fenomeno di ritardo temporale tra i diversi raggi prende il nome di
dispersione intermodale. Infatti i vari cammini percorsi dai raggi possono
essere considerati come modi di propagazione dell’onda luminosa all’interno
della fibra.
•Ad ognuno di questi modi può essere associata una velocità di
propagazione lungo l’asse della fibra pari a:
csin
vg 
n1
che dipende dall’angolo di incidenza  del raggio sull’interfaccia nucleomantello e quindi dalla natura del modo.
•Per questo motivo le fibre step-index a nucleo largo sono anche fibre
multimodo e sono caratterizzate dalla dispersione intermodale.
D.I.B.E.-Università di Genova
34
Effetti della Dispersione Intermodale nelle fibre StepIndex Multimodo sulle trasmissioni numeriche
•La dispersione intermodale si rivela dannosa quando il ritardo relativo
massimo t nella propagazione dei modi diviene confrontabile con le costanti
di tempo del segnale trasmesso in fibra.
•Se viene lanciato in fibra un impulso di durata T mediante uno dei raggi più
lenti (ovvero con angolo di incidenza esterno q = qa), la durata di tale impulso,
osservato alla distanza L sulla fibra sarà pari a T+t.
•Quando t diviene confrontabile con T, l’impulso trasmesso si “allarga” e tende
ad “invadere “gli intervalli di segnalazione adiacenti (vedi figura sotto). Si
determina quindi interferenza inter-simbolica (ISI)
D.I.B.E.-Università di Genova
35
Effetti della Dispersione Intermodale nelle fibre StepIndex Multimodo sulle trasmissioni numeriche
•La dispersione intermodale impone quindi un limite superiore alla velocità
di trasmissione, che deve essere scelta in modo tale da non avere ISI. In
pratica:
Ln 2
1
t 
1
cn2
 T 
Rb
•Considerando la banda di trasmissione B circa uguale al bit-rate Rb, si ottiene
inoltre che:
cn2
B
Ln12
•Introducendo il parametro di capacità =BL, si ottiene infine:
cn2
 2
n1
•Con i valori di n1 ed n2 usuali (1.50 ed 1.47 rispettivamente) si ottiene un
valore della capacità di 10Mb/s*Km, che è un valore alquanto modesto.
D.I.B.E.-Università di Genova
36
Fibre ad indice graduato (Graded-Index)
•Per ovviare ai problemi di dispersione intermodale tipici delle fibre step-index
multimodali, si possono fabbricare fibre di differente tipo.
•Restando nell’ambito delle fibre a nucleo largo, si sono realizzate fibre il cui
indice di rifrazione del nucleo varia gradatamente tra un valore massimo n1
ed il valore del mantello n2, man mano che ci si sposta dal centro della fibra
verso il mantello.
•Questo tipo di fibra è detto ad indice graduato (graded index).
D.I.B.E.-Università di Genova
37
Fibre Graded-Index: caratteristiche della propagazione
•Nelle fibre graded-index i raggi non subiscono una riflessione brusca
all’interfaccia nucleo-mantello, ma vengono “incurvati” dalla variazione
graduale dell’indice di rifrazione del nucleo.
•La principale legge di variazione di n con la distanza radiale r è il cosiddetto
profilo :
n
n2

 n1 1  2r a  r  a (nucleo)
n r   

r  a (mantello)
n2
n1
r
•a è il raggio del nucleo e  è un parametro definito in sede di lavorazione.
•Le traiettorie di propagazione possono essere ricavate mediante il principio
di Fermat, secondo il quale il percorso scelto da un raggio per propagarsi tra
un punto P1 di partenza ed un punto P1 di arrivo è quello che minimizza il
tempo totale di percorrenza.
D.I.B.E.-Università di Genova
38
Fibre Graded-Index: caratteristiche della propagazione
•Il tempo dt necessario a percorrere un tratto di lunghezza elementare ds,
relativo al generico punto r, caratterizzato da indice di rifrazione n(r) è pari a:
dt 
ds n(r )ds

v
c
•Considerando il principio di Fermat, la traiettoria seguita dal raggio è tale da
minimizzare l’integrale curvilineo:
P2
 n(r)ds
P1
che è proporzionale al tempo di propagazione totale.
D.I.B.E.-Università di Genova
39
Fibre Graded-Index: caratteristiche della propagazione
•Il principio di Fermat può essere riformulato in maniera differenziale (equazione di
Eulero-Lagrange), ovvero:
d 
dr 
n
(
r
)

  n(r )
ds 
ds 
•Adottando un sistema di riferimento come quello della figura sottostante, tale
equazione può essere semplificata nella seguente maniera, per ottenere
l’equazione cartesiana y(z) del raggio luminoso:
d 2 y 1 dn

2
n dy
dz
r y
(distanza radiale)
Ove n è funzione di r,
secondo il profilo 
D.I.B.E.-Università di Genova
40
Fibre Graded-Index: caratteristiche della propagazione
•Sostituendo n(r) precedentemente indicata, con  = 2 (profilo parabolico) e
considerando <<1 (condizione verificata nella pratica), si trova l’equazione di un
oscillatore armonico, la cui soluzione è la seguente:
y0'
z
z


y( z )  y0 cos 2  
sin  2 
a
a
2 / a 

•Ove y0 e y’0 sono la posizione e la direzione iniziale del raggio. Due raggi che
partono dalla stessa posizione, ma con direzioni iniziali differenti si propagano
seguendo traiettorie diverse, che seguono un andamento sinusoidale con
diverse ampiezze (vedi figura slide precedente).
•In questo modo la dispersione intermodale viene attenuata, in quanto, per effetto
della graduazione dell’indice di rifrazione, i raggi che si allontanano
maggiormente dall’asse seguendo traiettorie più lunghe, si trovano a transitare in
zone della fibra caratterizzate da un indice di rifrazione più piccolo, rispetto a
quello che si ha in vicinanza dell’asse.
•L’allungamento della traiettoria è quindi compensato da una maggiore velocità
di propagazione. In pratica la risposta della fibra viene “equalizzata”.
D.I.B.E.-Università di Genova
41
Fibre Graded-Index: incremento delle prestazioni rispetto
alle fibre step-index
•Sfortunatamente, i risultati dell’analisi mostrata in precedenza, valgono solo per i
raggi meridionali, cosicché un certo grado di dispersione è presente anche nelle
fibre graded-index.
• Si può dimostrare che le fibre a profilo  presentano presentano un ritardo
differenziale minimo pari a:
n12
t 
L
8c
quando si sceglie:
  21    2
Questo è il motivo per cui si sceglie 2, come già accennato. La dispersione
minima conduce ad un valore massimo della capacità per fibra multimodo graduata
pari a:
8c

Valori tipici: 4Gbit/s*Km
2
n1
D.I.B.E.-Università di Genova
42
Fibre monomodali a nucleo stretto
•Il rimedio più efficace per risolvere il problema della dispersione intermodale
sarebbe, teoricamente, quello di inibire la propagazione dei modi multipli in
fibra, lasciando un solo modo fondamentale.
•Sfortunatamente questa condizione, detta di monomodalità, non può essere
ricavata mediante l’approccio semplificato dato dall’ottica geometrica, usato per la
fibra multimodo.
•La monomodalità richiede una configurazione della fibra a “nucleo stretto”
(<<50m), in modo tale che le dimensioni caratteristiche della fibra risultino
confrontabili con la lunghezza d’onda del segnale (0.8 -1.6m).
•In queste condizioni si deve ricorrere ad un approccio più formale per studiare le
caratteristiche di propagazione del segnale attraverso la fibra ottica: ovvero
l’approccio basato sulle equazioni di Maxwell.
D.I.B.E.-Università di Genova
43
Propagazione di un’onda elettromagnetica in una Fibra
Step-Index (approccio formale con equazioni di Maxwell)
•Precisiamo innanzitutto la notazione adottata. Adottando il formalismo degli
equivalenti in banda-base di segnali passabanda (o inviluppi complessi), un
campo elettrico generico può essere espresso come:


E r , t   Re  E r , t e j 2f 0t 


r   x, y , z 
T
Vettore posizione
Equivalente in banda-base rispetto
alla frequenza f0 del campo elettrico.
•Nel caso di campo monocromatico si ha che:


E r , t   E r 
D.I.B.E.-Università di Genova
44
Propagazione di un’onda elettromagnetica in una Fibra
Step-Index (approccio formale con equazioni di Maxwell)
•L’analisi della propagazione del segnale ottico in una fibra di tipo step-index parte
dalle equazioni di D’Alembert delle onde:
2

E
2
 E   2
t
2 H
 H  
t 2
2
•Riscrivendo tali equazioni attraverso l’inviluppo complesso di un campo
monocromatico (altrimenti detto fasore) in un materiale dielettrico omogeneo,
isotropo e senza perdite, otteniamo la cosiddetta equazione di Helmoltz:

 r 


  r   n k  r   0
2
2
2
0
è una qualsiasi tra le sei componenti dei vettori complessi


E H
k0  2f 0 c è il numero d’onda nel vuoto dell’oscillazione accoppiata alla fibra.
n è l’indice di rifrazione nel mezzo.
D.I.B.E.-Università di Genova
45
Propagazione di un’onda elettromagnetica in una Fibra
Step-Index (approccio formale con equazioni di Maxwell)
•In un sistema di riferimento a coordinate cilindriche (r,f,z), avente asse z
coincidente con l’asse longitudinale della fibra nella direzione di propagazione
dell’onda, l’equazione di Helmoltz diventa:



z


 2  1 
1 2 2
2 2

 2
 2  n k0   0
2
2
r
r r r f
z
con n=n1 se 0 
(i)
r  a (nucleo) e n=n2 se r  a (mantello)
•A questo punto si richiede che la soluzione dell’equazione (i) abbia la seguente
forma:

 r , f , z   F r f  exp  jz 
(ii)
•che, in ogni punto della fibra, fissati r e f, rappresenta un’onda progressiva
lungo l’asse z, con coefficiente di propagazione  da determinarsi.
D.I.B.E.-Università di Genova
46
Propagazione di un’onda elettromagnetica in una Fibra
Step-Index (approccio formale con equazioni di Maxwell)
•Sostituendo (ii) in (i) si ottiene:


d 2 F 1 dF
2 2
2


n
k


F
0
2
2
  dr
r dr

0
2
2
f
F r
(iii)
•Il termine che moltiplica la funzione  è una costante rispetto alla coordinata f.
Per cui la (iii) può essere spezzata in due equazioni differenziali ordinarie per le
funzioni f e F(r). Poiché la funzione  deve risultare periodica di periodo 2
nella variabile f, l’equazione relativa deve essere scritta nella seguente maniera:
d 2
2

m
0
2
df
(iv)
•ove m è una costante intera arbitraria per rispettare la condizione di periodicità.
D.I.B.E.-Università di Genova
47
Propagazione di un’onda elettromagnetica in una Fibra
Step-Index (approccio formale con equazioni di Maxwell)
•L’equazione per F(r) è allora un’equazione del secondo ordine di Bessel:
2

d 2 F 1 dF  2 2
m
2

  n k0    2  F  0
2
dr
r dr 
r 
(v)
•Affinché l’onda sia confinata all’interno del nucleo (ossia venga guidata), la
costante di propagazione  deve soddisfare le seguenti due condizioni:
  n1k0 0  r  a
(costante di propagazione minore del numero
d’onda del nucleo)
(costante di propagazione maggiore del
  n2 k0 r  a
numero d’onda del mantello)
(Verificheremo
•E’ quindi conveniente definire due nuove costanti:
dopo perché)
2
2
2
(nel
nucleo)
  nk  0


 2    n2 k0 2  0
1 0
2
(nel mantello)
D.I.B.E.-Università di Genova
48
Propagazione di un’onda elettromagnetica in una Fibra
Step-Index (approccio formale con equazioni di Maxwell)
•L’equazione (v) assumerà quindi due forme diverse, una relativa al nucleo della
fibra ottica ed una relativa al mantello, ovvero:
d 2 F 1 dF  2 m2 

   2  F  0 0  r  a
2
dr
r dr 
r 
d 2 F 1 dF  2 m 2 

    2  F  0
2
dr
r dr 
r 
ra
(v.i)
(v.ii)
•Le equazioni (v.i) e (v.ii) ammettono diversi tipi di soluzioni generali, dette funzioni
di Bessel, che sono definite in forma numerica.
•Si devono scartare le funzioni di Bessel che non sono limitate in r=0 (poiché il
campo elettrico assume valori finiti in tale punto). Così come si devono scartare le
funzioni di Bessel che non sono limitate per r tendente all’infinito, poiché si
richiede che il campo si esaurisca interamente nel mantello (supposto di spessore
infinito).
D.I.B.E.-Università di Genova
49
Propagazione di un’onda elettromagnetica in una Fibra
Step-Index (approccio formale con equazioni di Maxwell)
Funzioni di Bessel di prima specie
D.I.B.E.-Università di Genova
50
Propagazione di un’onda elettromagnetica in una Fibra
Step-Index (approccio formale con equazioni di Maxwell)
Funzioni di Bessel di seconda specie
(Per x->0, tendono a -)
D.I.B.E.-Università di Genova
51
Propagazione di un’onda elettromagnetica in una Fibra
Step-Index (approccio formale con equazioni di Maxwell)
Funzioni di Bessel modificate di prima specie (Per x->+, tendono a + )
D.I.B.E.-Università di Genova
52
Propagazione di un’onda elettromagnetica in una Fibra
Step-Index (approccio formale con equazioni di Maxwell)
Funzioni di Bessel modificate di seconda specie
D.I.B.E.-Università di Genova
53
Propagazione di un’onda elettromagnetica in una Fibra
Step-Index (approccio formale con equazioni di Maxwell)
•Da quanto visto nei grafici riportati precedentemente sulle funzioni di Bessel, le
uniche funzioni ammissibili come soluzioni dell’equazione di Helmoltz sono
quelle di prima specie (Jm) e quelle modificate di seconda specie (Km). La
soluzione di (v.i) e (v.ii) viene quindi esplicitata nella seguente maniera.

  r , f , z   A J m r  exp  jmf  exp  jz  r  a


  r , f , z   B K m r  exp  jmf  exp  jz r  a
(vi)
•Le costanti A e B sono determinate sulla base delle condizioni al contorno.
Esempi di andamenti delle soluzioni dell’equazione di Helmoltz sono mostrati sotto:

 r ,f , z 
è una qualsiasi tra le 6 componenti
dei vettori degli equivalenti in bandabase di E e di H. Quindi vi sono da
determinare 12 costanti.
D.I.B.E.-Università di Genova
54
Propagazione di un’onda elettromagnetica in una Fibra
Step-Index (approccio formale con equazioni di Maxwell)
•Il numero di costanti da determinare può essere, tuttavia, ridotto. Attraverso le
equazioni di Maxwell è possibile infatti esprimere le componenti radiali e le
componenti tangenziali del campo magnetico e del campo elettrico in funzione
delle sole componenti assiali, ovvero:
E r  E r E z  H r  H r H z 
Ef  Ef E z 
H f  H f E z 
•Le costanti da determinare rimangono in questo modo solamente quattro (due
relative alle componenti assiali del campo elettrico e due relative alle componenti
assiali del campo magnetico). Queste costanti possono essere, infine, determinate
imponendo le condizioni di continuità delle componenti tangenziali ed assiali
all’interfaccia in r=a (interfaccia nucleo-mantello).
•Si ricava in tal modo un sistema a 4 equazioni e 4 incognite, che ammette
soluzione non banale solo se il determinante della matrice dei coefficienti è non
nullo. Questa condizione è detta equazione caratteristica.
D.I.B.E.-Università di Genova
55
Propagazione di un’onda elettromagnetica in una Fibra
Step-Index (approccio formale con equazioni di Maxwell)
•Omettendo i calcoli, l’equazione caratteristica ha la seguente formulazione
(l’apice indica l’operazione di derivazione):
 J m' a 
K m' a   J m' a  n22 K m' a    m 


  


 2
 aJ m a  aK m a   aJ m a  n1 aK m a    n1k0 
2
2
 1
1 


 a 2  a 2  (vii)


•L’andamento oscillatorio delle funzioni di Bessel Jm suggerisce che fissato l’ordine
m di armonica della soluzione elementare dell’equazione di Helmoltz secondo la
(vi.i) e (vi.ii), si hanno in generale soluzioni multiple dell’equazione
caratteristica, ognuna di esse contraddistinta da un diverso valore della costante
di propagazione . Tali valori sono indicati con mi, ove m è l’ordine di armonica
(ovvero l’ordine della funzione di Bessel) ed i è l’ordine della soluzione.
•Ognuno dei valori sopracitati corrisponde ad un modo distinto di propagazione
dell’onda in fibra, caratterizzato da una specifica costante di propagazione e da
una particolare distribuzione radiale del campo.
D.I.B.E.-Università di Genova
56
Propagazione di un’onda elettromagnetica in una Fibra
Step-Index (approccio formale con equazioni di Maxwell)
•A questo punto possiamo capire perché devono verificarsi le due condizioni
relative alla costante di propagazione precedentemente indicate in modo tale da
garantire il confinamento dell’onda all’interno del nucleo, ovvero:
  n1k0 0  r  a
  n2 k0 r  a
•Introduciamo la seguente quantità che chiameremo indice di modo, ovvero:
n ˆ  k0
•In effetti, ogni modo all’interno della fibra si propaga con un indice di rifrazione n,
che deve rispettare le due condizioni:
n1  n  n2
D.I.B.E.-Università di Genova
57
Propagazione di un’onda elettromagnetica in una Fibra
Step-Index (approccio formale con equazioni di Maxwell)
•Infatti, un modo cessa di essere guidato, quando:
n  n2
(*)
•Questo può essere visto considerando l’andamento della funzione di Bessel
soluzione dell’equazione di Helmoltz nel mantello. Per valori molto elevati
dell’argomento essa può essere approssimata come:
Km r   exp  r 
2r
r  1
•Quando è verificata la condizione (*), si ha che:
n   k0  n2  nk0    n2 k0
•E quindi 2<=0. Ciò significa che non si ha più il decadimento esponenziale del
campo all’interno del mantello (avremmo una funzione di Bessel che diviene
un’esponenziale complessa). Il campo si propaga anche nel mantello. Se =0
(ovvero se n = n2) si dice che il modo raggiunge la condizione di cutoff.
D.I.B.E.-Università di Genova
58
Determinazione del numero dei modi di propagazione in
una fibra step-index a nucleo stretto
•Ricavare il numero dei modi di propagazione supportati da una fibra step-index a
nucleo stretto non è un’operazione immediata.
•Occorre inanzitutto definire un nuovo parametro, detto parametro V della fibra o
anche frequenza normalizzata:
V ˆ a  2   2  ak0 n12  n22  ak0 NA  2aNA 0
•Il parametro V è facilmente determinabile in funzione delle specifiche standard
della fibra (apertura numerica, raggio del nucleo). Tuttavia esso è fondamentale
nella determinazione del numero dei modi di propagazione della fibra step-index.
•Dato che:
 2   2  n2 k0 2     2  n2 k0 2
•Si ottiene infine che:
 n2V 
2
   

 aNA 
2
(costante di
propagazione)
D.I.B.E.-Università di Genova
(viii)
59
Determinazione del numero dei modi di propagazione in
una fibra step-index a nucleo stretto
•Sostituendo la (viii) in (vii), si ottiene un’equazione in due incognite: a e a, che
possiamo interpretare in maniera grafica come l’equazione implicita di una
famiglia di curve sul piano (a, a), ciascuna individuata da un’armonica di ordine
m. Fissato m, ogni punto della relativa curva rappresenta una possibile coppia di
valori (a, a), relativi ad un modo della fibra.
•Nella figura della slide precedente sono rappresentate le famiglie di curve per m=0
(tratto nero spesso) e m=1 (tratto grigio). Tuttavia tali curve non ci dicono quanti e
quali modi sono effettivamente supportati dalla fibra ottica alla lunghezza
assegnale 0.
•Questa informazione si ricava tenendo conto che:
V ˆ a  2   2  a   a   V 2
2
2
Equazione di una circonferenza di raggio V
D.I.B.E.-Università di Genova
60
Determinazione del numero dei modi di propagazione in
una fibra step-index a nucleo stretto
•Le intersezioni tra le famiglie di curve e la circonferenza di raggio V
rappresentano le coppie di valori (a, a), relative ai modi di propagazione
effettivamente supportati dalla fibra ottica. Da queste coppie di valori, si può risalire
al coefficiente di propagazione  di ogni modo supportato.
D.I.B.E.-Università di Genova
61
Determinazione del numero dei modi di propagazione in
una fibra step-index a nucleo stretto
•Il parametro V è direttamente proporzionale all’apertura numerica della fibra.
Questo incontra quanto osservato in precedenza dall’analisi condotta con
l’ottica geometrica per le fibre a nucleo largo, laddove più ampia è l’apertura
numerica e più largo è il cono di accettazione dei raggi ed, in definitiva, maggiore il
numero dei modi di propagazione supportati.
•Dalla figura riportata nella slide precedente, si osserva come, per quanto piccolo
sia il valore di V, almeno una intersezione tra una circonferenza ed una delle
curve della famiglia m = 1 esisterà sempre.
•Si può dimostrare (qui viene omesso) che se V<2.405, tale intersezione è unica,
anche in presenza delle altre famiglie di curve con m>1, che nel grafico non sono
rappresentate. Infatti si può verificare che V=2.405 è il valore per il quale tutti gli
altri modi della fibra, eccetto quello fondamentale, sono nella condizione di
cutoff (ovvero non possono propagarsi in maniera guidata). La condizione di
monomodalità della fibra ottica è quindi:
V  2.405
Condizione di monomodalità
D.I.B.E.-Università di Genova
62
Determinazione del numero dei modi di propagazione in
una fibra step-index a nucleo stretto
•La curva sperimentale che riporta il numero di modi supportati M da una fibra
step-index in funzione del parametro V è mostrata nella figura sottostante. Sono
anche indicate le due curve di upper e lower bound che “racchiudono” la curva
sperimentale. Ciascun modo può essere caratterizzato da diverse polarizzazioni.
V2
M
2
Valori medio-piccoli di V
M  2
4V 2

Valori grandi di V
(viii)
D.I.B.E.-Università di Genova
63
Realizzazione pratica di una fibra step-index
monomodale
•Per concludere questa parte, si può dire che una fibra monomodale può essere
realizzata, in pratica, rispettando in sede di fabbricazione la seguente condizione:
V  2aNA 0  2an1 2 0  2.405
•I due parametri costruttivi su cui si può agire sono il raggio del nucleo a e la
variazione relativa dell’indice di rifrazione . Occorre pertanto ridurre o uno o
l’altro o entrambi.
•La riduzione eccessiva del raggio del nucleo crea difficoltà di accoppiamento
della fibra alle sorgenti ed ai fotorivelatori e rende problematiche le giunzioni
durante la posa. Per questo si cerca di ridurre anche , in modo da non dover
realizzare fibre a nucleo troppo stretto.
•Tuttavia un valore troppo basso di  (nucleo e mantello con indici di rifrazione
quasi uguali) e quindi di NA, rende difficile fare entrare e propagare un raggio
all’interno della fibra (infatti l’angolo di accettazione qa diviene molto piccolo).
D.I.B.E.-Università di Genova
64
Realizzazione pratica di una fibra step-index
monomodale
•Per ovviare a questi inconvenienti, talora si utilizzano le cosiddette fibre W, dette
anche a mantello depresso.
•Queste fibre sono caratterizzate da un nucleo non troppo stretto e da un
doppio mantello. Il primo mantello ha un indice di rifrazione molto inferiore
rispetto a quello del nucleo (vedi figura sottostante) ed è molto sottile, mentre il
secondo mantello, di spessore maggiore del primo, ha un indice di rifrazione
comparabile con quello del nucleo. •Il modo fondamentale residuo è tale da verificare
la condizione:
n3k0    n1k0
•Eventuali altri modi di ordine superiore con:
n2 k0    n3k0
Non sono possibili in quanto il primo mantello
funge da barriera (per tali modi l’onda tende
a propagarsi nel primo mantello ed a
disperdersi successivamente nel secondo).
D.I.B.E.-Università di Genova
65
Dispersione intramodale in una fibra step-index
monomodale
•Fino ad ora abbiamo visto quali accorgimenti possono essere adottati per limitare
il fenomeno della dispersione intermodale, che è oggettivamente il massimo
fattore di limitazione della capacità di un collegamento in fibra.
•Le soluzioni adottate vanno dall’uso di fibre a nucleo largo, ma ad indice
graduato, all’impiego di fibre step-index monomodali (a nucleo stretto o a
mantello depresso).
•La soluzione più efficiente appare quella che utilizza fibre step-index
monomodali (altre soluzioni, come quella di utilizzare fibre ad indice graduato ed a
nucleo stretto non sono utili a migliorare le prestazioni e quindi non vengono
realizzate).
•Tuttavia anche le fibre monomodali soffrono di un fattore che limita la capacità del
collegamento. Questo fattore è la dispersione intramodale.
D.I.B.E.-Università di Genova
66
Dispersione intramodale in una fibra step-index
monomodale
•La dispersione intramodale è dovuta al fatto che il vetro è un materiale lineare, ma
dispersivo, ovvero il suo indice di rifrazione dipende dalla lunghezza d’onda
dell’oscillazione luminosa a cui è sottoposto, ovvero:
n  n 
•Quindi segnali a lunghezza d’onda differenti si propagano nel mezzo a velocità
differenti. Questo fatto è assai rilevante nei sistemi di trasmissione in fibra, poiché il
segnale trasmesso è un segnale modulato, che è scomponibile in una
sovrapposizione di più oscillazioni monocromatiche a diverse lunghezze
d’onda (frequenze), centrata intorno alla frequenza della portante f0 (ovvero alla
lunghezza d’onda fondamentale 0).
•Questo tipo di segnale è detto pacchetto d’onda e la generica componente a
frequenza f del pacchetto d’onda si propaga con velocità di gruppo definita da:
1
ˆ
d   1 d  f  1 d  fn f  n f  f dn f 




d
2 df
c df
c
c df
vg  f 
n
(Ottica geometrica)
vg 
c
D.I.B.E.-Università di Genova
67
Dispersione intramodale in una fibra step-index
monomodale
•Se n non è costante rispetto alla frequenza, tali componenti si propagano con
velocità diverse ed, una volta raccolte all’estremità del mezzo, si ricombinano
con ritardi diversi, dando luogo ad una distorsione lineare analoga alla
dispersione temporale per cammini multipli.
•La distorsione cromatica può essere analizzata quantitativamente considerando
un pacchetto d’onda che si propaga lungo l’asse z in un mezzo omogeneo,
isotropo, lineare e semi-infinito. L’espressione del pacchetto d’onda è la seguente:




ψ  z;t   Re ψ  z;t  exp 2jf0t    Re az;t  exp 2jf0t   0 z  




Una qualunque delle sei
componenti del campo
elettromagnetico associato
all’onda luminosa
Inviluppo complesso
del pacchetto d’onda
Costante di
propagazione alla
lunghezza d’onda 0
  f 0  ˆ 2n f 0  0
D.I.B.E.-Università di Genova
68
Dispersione intramodale in una fibra step-index
monomodale
•A noi interessa calcolare una relazione che leghi la forma d’onda dell’inviluppo
complesso dell’onda inviata, con quella osservabile ad una distanza z
dall’imboccatura della fibra, ovvero:

a  z;t 


T a 0;t 




a0;t    0;t 
•Poiché la distorsione è lineare, possiamo attribuire alla relazione che lega i due
inviluppi complessi il significato di una relazione ingresso-uscita di un sistema
lineare, che può essere completamente caratterizzato dalla propria risposta in
frequenza.
•Per calcolare tale risposta in frequenza, supponiamo che:

a0;t   exp  j 2t 
Oscillazione sinusoidale
a frequenza 
D.I.B.E.-Università di Genova
69
Dispersione intramodale in una fibra step-index
monomodale
•Per cui, nelle ipotesi fatte in precedenza, avremo che:

az;t   H   exp  j 2t 
Risposta in frequenza della distorsione intramodale
•Per cui, il pacchetto d’onda è esprimibile come:

 z;t   H   exp  j 2t  exp  j 0 z 
(i)
•Ritornando, tuttavia, alla definizione letterale di pacchetto d’onda, si può scrivere
un’altra eguaglianza:


 z;t    0;t  exp  j  f 0   z   exp 2jt  exp  j  f 0   z  (ii)
D.I.B.E.-Università di Genova
70
Dispersione intramodale in una fibra step-index
monomodale
•Eguagliando (i) con (ii) otterremo la risposta in frequenza del mezzo dispersivo:
H    exp j  f 0      f 0 z
•Se l’indice di rifrazione non dipendesse dalla frequenza (mezzo non dispersivo),
si otterrebbe:
  f 0      f 0   2n c
•E quindi non si avrebbe alcuna distorsione durante la propagazione, ma
solamente un ritardo proporzionale alla lunghezza del tragitto percorso, ovvero:
g 
z

D.I.B.E.-Università di Genova
71
Dispersione intramodale in una fibra step-index
monomodale
•Se invece si considera la fibra un mezzo debolmente dispersivo (qual è), ovvero
si considerano variazioni modeste dell’indice di rifrazione in funzione della
frequenza, è lecito approssimare l’andamento di (f) con un polinomio di Taylor
attorno ad f0 ed arrestato al II° ordine. In tal caso si ottiene:

 d
H    exp  j
df


2



 1d 
z  exp  j
2
2
df


f  f0




 z

f  f0

2
•La relazione scritta sopra può essere espressa in funzione della velocità di
gruppo, precedentemente definita e del coefficiente di dispersione cromatica,
definito come:
D ˆ
d 1 vg 
d

d 1 vg  df
df
c 1 d 2
 2
d
 2 df 2
D.I.B.E.-Università di Genova
72
Dispersione intramodale in una fibra step-index
monomodale
•In tal modo si ottiene la seguente espressione della distorsione cromatica:

 2 D20 z 
z


H    exp  j 2  exp  j

vg 
c 




Termine di distorsione di fase
(nullo se il mezzo non è dispersivo,
mentre dipende da D se lo è)
Termine che introduce un ritardo di
propagazione (ritardo di gruppo)
•A questo punto, possiamo abbandonare l’ipotesi di materiale semi-infinito e
ritornare al caso della fibra ottica step-index monomodale, usando l’indice di
modo, che è espresso come rapporto tra la costante di propagazione ed il numero
d’onda, ovvero:
N  f  ̂
f 
k
D.I.B.E.-Università di Genova
73
Dispersione intramodale in una fibra step-index
monomodale
•L’indice di modo risulta variabile con f poiché il materiale è dispersivo (in quanto 
dipende da n). Ricordando quindi la definizione di velocità di gruppo, avremo che:
 d kN  f 
 d  fN  f  c 
c
 d  
v g  f  ˆ 








df
Ng  f 
 d 
 d 2f 


1
Ove:
dN  f 
N g  f  ̂ N  f   f
df
1
1
Indice di gruppo, che lega la
velocità di gruppo della
componente del pacchetto d’onda a
frequenza f con la corrispondente
velocità nel vuoto.
•Le diverse componenti spettrali del segnale in fibra aventi differenti lunghezze
d’onda si propagheranno quindi con velocità di gruppo in generale diverse.
L’impulso sarà tanto più distorto quanto più forte è la dipendenza di N da f.
D.I.B.E.-Università di Genova
74
Dispersione intramodale in una fibra step-index
monomodale
•Supponiamo che lo spettro del segnale trasmesso si estenda su una banda B
centrata attorno alla frequenza di portante f0, che corrisponde ad una larghezza
spettrale  centrata su 0. Il ritardo differenziale massimo relativo alle
componenti in tale banda, associate ad un impulso di durata T, propagatosi in fibra
per una lunghezza L sarà esprimibile come:
d L vg 
dt
t 
 

d
d
•Introducendo il coefficiente di dispersione cromatica D si ottiene, infine:
t  L
d 1 vg 
d
  L D 
•Il coefficiente di dispersione cromatica D, misurato in psec/nm*Km, indica
l’aumento di durata di un impulso (in psec) caratterizzato da una certa larghezza
spettrale  (misurata in nm), che ha viaggiato in fibra per 1 Km.
D.I.B.E.-Università di Genova
75
Dispersione intramodale in una fibra step-index
monomodale
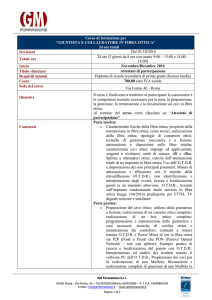
•L’andamento tipico di D in funzione della lunghezza d’onda è mostrato nella Figura
sottostante, dalla quale si può desumere che D è nullo per valori di  pari a circa
1.3m (seconda finestra). Il valore di D per quel che riguarda la terza finestra
(=1.55m) è invece pari a 17 psec/km*nm.
•In realtà la completa nullità delle dispersioni cromatiche non è praticamente
raggiungibile e, lavorando in seconda finestra, si può arrivare a valori realistici di D
pari a 1 psec/km*nm.
D.I.B.E.-Università di Genova
76
Dispersione intramodale in una fibra step-index
monomodale (limitazione alla capacità della fibra)
•Supponendo che l’estensione spettrale del segnale  sia circa uguale a 1nm
(possibile da ottenere con una sorgente LASER a basso costo) e di lavorare in
seconda finestra con D = 1 psec/nm*Km, si ottiene che:
t  L D   T  B 
1
1
 BL 
L D 
D 
pari a 1Tbit/sec*Km
condizione per non avere ISI
•Da questi numeri si capisce come la condizione di monomodalità in una fibra
ottica consenta di raggiungere elevati valori di capacità, di svariati ordini di
grandezza superiori a quelli ottenuti con fibre multimodali, sia di tipo step-index,
che ad indice graduato.
D.I.B.E.-Università di Genova
77
Banda passante di un canale in fibra ottica
•Da quanto visto finora, si può affermare che il coefficiente di distorsione cromatica
può essere espresso come la somma di due coefficienti:
•DM, che è il coefficiente di sola dispersione cromatica relativo al materiale
(unica fonte di dispersione nelle fibre monomodali);
•DW, che è la dispersione di guida d’onda, dipendente dalla geometria della
fibra (termine legato alla dispersione intermodale delle fibre a nucleo largo).
•La caratteristica dispersiva del materiale si traduce in un comportamento
passabasso della risposta in frequenza del canale in fibra ottica. Vedremo
questo tipo di comportamento prima per le fibre ottiche monomodali, dove la
frequenza di taglio della risposta del canale sarà legata alla dispersione
intramodale e poi per le fibre ottiche multimodali, ove occorrerà tenere conto
anche dell’influenza della dispersione intermodale.
D.I.B.E.-Università di Genova
78
Banda passante di una fibra ottica monomodale
•Da quanto abbiamo visto, l’effetto distorcente sul segnale trasmesso esercitato da
una fibra ottica monomodale è essenzialmente un suo allargamento temporale. Se,
pertanto, l’eccitazione in ingresso s(t) alla fibra è un impulso matematico, l’uscita
h(t) tenderà a divenire un impulso ad andamento Gaussiano, come mostrato
nella Figura sottostante:
s(t)
h(t)
ht  
t
1
2   2

exp  t 2 2  2
2
t

D.I.B.E.-Università di Genova
   t  L D 
79

Banda passante di una fibra ottica monomodale
•Poiché l’allargamento temporale dell’impulso  è limitato da una quantità
proporzionale alla lunghezza della tratta della fibra ottica, è ragionevole supporre
che anch’esso sarà proporzionale a tale lunghezza, per cui si potrà esprimere
come:
   k L
•La costante k dipende dalla lunghezza d’onda di trasmissione (poiché il
materiale è dispersivo) e dall’allargamento spettrale del segnale trasmesso ,
quest’ultima è caratteristica propria del dispositivo di trasmissione (è molto piccolo
nei diodi di tipo LASER, indicato nell’ordine di 1nm).
•La risposta in frequenza della fibra monomodale è pertanto esprimibile come:
 1 2 2 2
H   f   ht   exp      f 
 2

D.I.B.E.-Università di Genova
Che ha caratteristiche
passabasso
80
Banda passante di una fibra ottica monomodale
•Si assume che la frequenza di taglio della caratteristica passabasso della fibra
ottica monomodale sia la frequenza in corrispondenza della quale il valore di H(f)
sia la metà di quello assunto in f=0. Questo valore è dato da:
f 
log e 4

•Poiché sappiamo che  è funzione di L attraverso la costante k, potremo scrivere
che:
F
f 
L
ove:
F  
in caso di completa
assenza di dispersione
cromatica (condizione
ideale difficile da ottenere)
log e 4
F 
k
(espresso in GHz*Km)
D.I.B.E.-Università di Genova
81
Banda passante di una fibra ottica monomodale
•In particolare, avremo che la risposta in frequenza di una fibra ottica monomodale
potrà essere espressa nella seguente maniera:

H   f   exp  log e 2   f fT 
2

•fT = f è la frequenza di taglio della fibra ottica monomodale. Se la banda del
segnale trasmesso è molto minore della frequenza di taglio, allora si può supporre
che la linea di trasmissione non introduca nessuna distorsione lineare.
•Altrimenti si deve supporre che una qualche distorsione sia introdotta e quindi
sia necessario utilizzare una qualche forma di equalizzazione in ricezione, in
maniera analoga a quanto già visto per le linee in cavo coassiale.
D.I.B.E.-Università di Genova
82
Banda passante di una fibra ottica multimodale
•Nel caso in cui si consideri l’utilizzo (invero svantaggioso) delle fibre ottiche
multimodali, la funzione di trasferimento della fibra ottica avrà una caratteristica
passabasso ancora più accentuata, in quanto alla dispersione intramodale, dovuta
alla natura dispersiva del materiale si aggiunge la dispersione intermodale,
dovuta alla presenza di diversi modi di trasmissione nella fibra.
•Abbiamo visto che il massimo ritardo differenziale dovuto alla dispersione
intermodale è pari a:
Ln12
t 

cn2
•Quindi, l’allargamento temporale dell’impulso dovuta alla dispersione intermodale
m è anch’esso proporzionale alla lunghezza della tratta in fibra. E quindi avremo:
 m  km L  t
D.I.B.E.-Università di Genova
km dipende dalla
lunghezza d’onda
83
Banda passante di una fibra ottica multimodale
•Per cui, la risposta in frequenza di una fibra ottica multimodale potrà essere
espressa come:


 1

H M  f   ht   exp    2  2   m2 f 2 
 2

•Ritornando alla notazione vista precedentemente, che utilizza la frequenza di
taglio, ossia:

H M  f   exp  log e 2   f fT 
2

•Avremo che:
fT 
1
2
2
L
L

Fm2 F2
log e 4
Fm 
km
D.I.B.E.-Università di Genova
Nel caso di fibre
monomodali:
Fm  
84
Caratteristiche di attenuazione delle fibre
ottiche
•Finora nella trattazione sulle caratteristiche di propagazione delle fibre ottiche
abbiamo tralasciato gli aspetti relativi alla perdita di potenza sperimentata dal
segnale luminoso durante la propagazione in fibra.
•Si può verificare sperimentalmente che l’attenuazione della potenza del
segnale trasmesso in una fibra ottica ha un andamento esponenziale in funzione
della lunghezza del tipo “classico”, ovvero:
PL   Pine L
D.I.B.E.-Università di Genova
85
Coefficiente di attenuazione
•Il coefficiente di attenuazione viene usualmente espresso in dB/km, ovvero:
 dB / Km  10 log PL  Pin   10 log e 
1
L
•Il coefficiente di attenuazione è una caratteristica costruttiva della fibra ottica.
Attualmente sono stati raggiunti valori di circa 0.2dB/Km per la terza finestra di
trasmissione ( = 1.55m).
•Oltre alla perdita di potenza a causa della distanza, vi sono altre fonti di
attenuazione del segnale in fibra, che qui citeremo soltanto:
•Perdita per assorbimento da materiale, dovuta alla presenza nel vetro di
impurità metalliche (ad es. Cu, Co, Cr, Fe), oppure di gruppi di ossidrile
imprigionati nel reticolo vetroso;
•Perdita per diffusione di Rayleigh, provocata da disomogeneità del
materiale su scala più piccola della lunghezza d’onda, che determinano
variazioni microscopiche dell’indice di rifrazione;
•Perdita per imperfezioni di guida, dovuta a piegature e microfratture della
fibra che avvengono durante la posa o per cause meccaniche.
D.I.B.E.-Università di Genova
86
Attenuazione di fibre di nuova generazione
D.I.B.E.-Università di Genova
87
PARTE TERZA:
DISPOSITIVI DI EMISSIONE E
RIVELAZIONE DEL SEGNALE OTTICO
D.I.B.E.-Università di Genova
88
Caratteristiche delle sorgenti luminose
Le sorgenti di segnale ottico per la conversione segnalepotenza luminosa sono:
LED (Light Emitting Diodes): sono diodi polarizzati in modo diretto, che
danno luogo ad emissione di fotoni, che sono funzione dell’intensità della corrente
che li attraversa. L’emissione di luce generata dalla giunzione viene solo
parzialmente convogliata nella fibra.
•Esistono LED a emissione di superficie (SLED) e LED a emissione
laterale (ELED), a seconda che la sezione terminale della fibra a contatto col
diodo sia disposta ortogonalmente rispetto al piano di giunzione o
parallelamente ad esso.
LASER (Light Amplification of Stimulated Emission of Radiation): sono
anch’essi diodi polarizzati in modo diretto, ma con una geometria a strati che
crea direzioni privilegiate di emissione ed un effetto di risonanza ottica.
D.I.B.E.-Università di Genova
89
Sorgenti LED
•I LED usati per scopi di telecomunicazione sono solitamente del tipo ad alta
efficienza, con radianze comprese tra 20 e 100W/angolo solido*cm2.
•A causa della natura isotropica della sorgente e dell’elevato indice di rifrazione del
semiconduttore, solo una piccola frazione della potenza generata fuoriesce dal
diodo, e solo una piccola parte di essa viene iniettata nella fibra. La massima
potenza iniettabile in una fibra può calcolarsi attraverso la seguente formula:


wTM  kRa   d 
2 
2
•Ra = radianza del diodo LED;
•d = min(2a,dL);
•2a = diametro del core;
•dL = diametro dell’area di emissione;
• = apertura numerica della fibra
•k vale 1 per fibre step-index e 2 per fibre graded-index.
D.I.B.E.-Università di Genova
90
Sorgenti LED
•Le caratteristiche corrente di eccitazione potenza luminosa di un diodo LED e di
un diodo LASER sono riportate nella figura sottostante. Si vede che la
caratteristica del diodo LED presenta un’accettabile linearità solo per potenze
emesse opportunamente inferiori al massimo valore.
WT
led
laser
I (mA)
•I diodi LED, inoltre, riducono la loro efficienza al crescere della frequenza della
corrente di eccitazione. Ciò è dovuto a dissipazioni legate alla capacità non nulla
della giunzione (il LED è assimilabile ad un circuito RC). Per cui i diodi LED hanno
un comportamento passabasso:
Hs  f  
1
1 j f fs
fs compresa tra 50 e 100MHz.
D.I.B.E.-Università di Genova
91
Sorgenti LASER
•Le sorgenti LASER sono caratterizzate da direzioni di emissione privilegiate
(quindi non sono sorgenti isotrope) e da effetti di risonanza ottica.
•La direttività dell’emissione consente di ridurre grandemente l’allargamento
spettrale del segnale luminoso prodotto ( pari a circa 1nm in seconda finestra
contro 0.25m registrati per una sorgente LED), e quindi di ridurre la dispersione
cromatica propria delle fibre ottiche (in particolare, nelle fibre monomodali, la
dispersione cromatica è l’unica fonte di distorsione del segnale).
•Anche l’efficienza spettrale delle sorgenti LASER è maggiore rispetto a quella
delle sorgenti LED. La frequenza di taglio fs è difatti dell’ordine di 1GHz.
•Di converso, le sorgenti LASER presentano caratteristiche sfavorevoli di non
linearità della caratteristica corrente di eccitazione potenza luminosa, soprattutto
per basse correnti di eccitazione (vedere figura nella slide precedente) ed una vita
media operativa piuttosto ridotta (circa 1/10 rispetto a quella dei LED).
D.I.B.E.-Università di Genova
92
Caratteristiche dei fotorivelatori
•Un fotorivelatore è un diodo polarizzato inversamente che dà luogo a
conduzione di corrente quando viene colpito da un fascio luminoso.
•Nella figura sottostante è mostrato un tipico circuito di fotorivelazione, in cui il
diodo viene attraversato da un fascio luminoso, produce una corrente i(t)
direttamente proporzionale alla potenza luminosa ricevuta e quindi una tensione
ad essa proporzionale ai capi di una resistenza R, che viene successivamente
amplificata e fatta passare attraverso un filtro con una opportuna funzione di
trasferimento.
fibra
i(t)
wR
R
Filtro
amplificatore
r(t)
-V
D.I.B.E.-Università di Genova
93
Funzionamento di un diodo fotorivelatore
•Il numero di fotoni al secondo costituenti il fascio incidente è dato da :
nf 

hc
wR
dove:
•wR è la potenza luminosa in uscita dalla fibra(Watt);
•h=6.62510-34 Js è la costante di Plank;
•c=3109 m/s è la velocità della luce;
• è la lunghezza d’onda della luce incidente;
• h   h  c è l’energia di un fotone.

•Un singolo fotone può dar luogo alla generazione di una
coppia elettrone/lacuna che attraversa la zona di
svuotamento, accelerata dalla tensione inversa, e produce
un impulso di corrente q(t) di durata estremamente breve
(1 nsec) e di area q (carica dell’elettrone=1.610-19).
D.I.B.E.-Università di Genova
94
Funzionamento di un diodo fotorivelatore
•Se la tensione inversa applicata al diodo è sufficientemente
elevata, l’elettrone generato da un fotone ha la possibilità di
generare altre coppie elettroni/lacune, dando luogo a g
impulsi di corrente q(t). Detto qi l’istante di arrivo del fotone i,
si ha che:

it    g i  qt  i 
i  
•in cui g i è una realizzazione della variabile aleatoria G,
di valore atteso m g e varianza  g2 . Questo effetto, detto
fotomoltiplicazione, o effetto valanga, non si verifica
se la tensione applicata al diodo è bassa.
D.I.B.E.-Università di Genova
95
Funzionamento di un diodo fotorivelatore
•Supponendo che il numero di arrivi al secondo abbia distribuzione di Poisson con
valore atteso:
  nf 

hc
wR
(in cui  è il rapporto (1) tra il numero di coppie elettroni/lacune generate e il
numero di fotoni incidenti), si ha che il valor medio della corrente prodotta dal
diodo è:
q Responsività
r ̂ 
iR  q  mg    mg  r  wR
hc del fotodiodo
La corrente in uscita dal fotodiodo può essere espressa come somma di un termine
costante (che è il valor medio) e di un termine tempo-variante che esprime lo
scostamento di tale grandezza dal valor medio, ovvero:
i t   iR  iq t 
iR è il valor medio nel tempo di i(t), che coincide con il suo valore atteso (processo ergodico);
iq(t) è il rumore quantico, e rappresenta la variabilità di i(t) attorno al suo valore medio.
D.I.B.E.-Università di Genova
96
Funzionamento di un diodo fotorivelatore
Diodo PIN: la tensione inversa applicata al diodo è bassa (30v), quindi l’effetto di moltiplicazione degli elettroni non si
2
verifica e risulta sempre g i  1 (per cui mg  1 e  g  0 ).
Diodo a valanga: la tensione inversa è elevata, mg è
controllabile attraverso il valore della tensione inversa. Si
definisce
il
FATTORE
DI
RUMORE
DEL
FOTOMOLTIPLICATORE(*):
Fg  1 
La curva
 g2 mg 
m
2
g
1
Fg  Fg mg  è stata determinata sperimentalmente :
Fg  mg2a
in cui a vale 0.5 per diodi al germanio e 0.150.25 per diodi al
silicio ( mg  300  400).
(*)Analogo del fattore di rumore del filtro visto per rumore termico nel
caso dei cavi
D.I.B.E.-Università di Genova
97
Fibre ottiche per comunicazioni e dispositivi
di emissione del segnale: status 1995
1a finestra
2a finestra
2a finestra
3a finestra
3a finestra
(multimodo)
(multimodo)
(monomodo)
(multimodo)
(monomodo)
3
0.4
0.35
0.25
0.2
Fm (GHzkm)
0.9
0.9

0.9

F (GHzkm)
0.10
1.2
1.2
0.1
0.15
0.16
4.0
4.0
0.2
0.25
2.0
6.5

6.3
6.3
-15
-17
-34
-18
-35
-9
-11
-22
-12
-23
8
5
3
4
2
Attenuazione
(dB/km)
SLED
F (GHzkm)
ELED
F (GHzkm)
LASER
Pot.emessa (dBm)
SLED
Pot.emessa (dBm)
ELED
Pot.emessa (dBm)
LASER
D.I.B.E.-Università di Genova
98
Gamma delle lunghezze d’onda per la trasmissione in fibra
L’ ITU-T ha suddiviso il campo delle lunghezze d’onda per
la trasmissione in fibra ottica nelle sei seguenti bande:
Banda
Nome
Campo
O - Band
Original
1260 – 1360 nm
E - Band
Extended
1360 – 1460 nm
S - Band
Short wavelength
1460 – 1530 nm
C - Band
Conventional
1530 – 1565 nm
L - Band
Long wavelength
1565 – 1625 nm
U - Band
Ultralong
wavelength
1625 – 1675 nm
Banda complessiva disponibile 50 THz
D.I.B.E.-Università di Genova
99
Altri problemi della trasmissione su fibra ottica
• Dispersione di polarizzazione
• Legata alla diversa velocità di propagazione delle due componenti
ortogonali del campo e.m.
• Effetto: allargamento dell’impulso nel tempo
• Dipendente da fattori di costruzione e posa della fibra e da
parametri fisici tempovarianti tra cui la temperatura
• Valori tipici compresi tra 0.2 e 0.5 ps/km-2
• Non linearità della fibra
• Per valori elevati di intensità del campo e.m. che attraversa la fibra,
l’indice di rifrazione può mostrare dipendenza dall’intensità stessa
• La non linearità più nota e problematica è l’interazione a quattro
fotoni (Four Wave Mixing FWM)
• Essa dà origine a repliche del sengale a lunghezze d’onda diverse
• Provoca quindi rumore e/o diafonia
• Il problema diventa rilevante in sistemi che trasmettono lunghezze
d’onda multiple D.I.B.E.-Università di Genova
100
PARTE QUARTA:
ANALISI DELLE PRESTAZIONI DI UN
COLLEGAMENTO IN FIBRA OTTICA
D.I.B.E.-Università di Genova
101
Prestazioni di un collegamento in fibra ottica per
trasmissioni analogiche
m(t)
Sorgente di
luce
M
s(t)
wT(t)
wR(t)
Fotodiodo
HC(f)
R
mgr
GT
wT(t)
e-L
HD(f)
M-1
HR(f)
HR(f)
wR(t)
iq(t)
r(t)
in(t)
La caratteristica corrente in ingressopotenza in uscita è
lineare solo se s t  soddisfa le seguenti limitazioni:
smin  GT  wmin  0
smax  GT  wmax  wTM
Max potenza nella fibra
D.I.B.E.-Università di Genova
102
d(t)
La funzione del blocco M è appunto quella di trasformare il
segnale utile allo scopo di rendere il segnale di eccitazione
tale da soddisfare queste limitazioni.
HD  f   e
 lge 2 f fT 2
Ritardo della fibra :viene trascurato come shift temporale,
se ne tiene conto come distorsione .((t) diventa gaussiana)
fibra :f=fT tale che HD(f) = 1/2 (non è proprio f. di taglio)
Osservazione: Se la banda occupata dal segnale wT t  è
sensibilmente inferiore al valore di fT , H D  f   1 nella banda
occupata dal segnale e la fibra NON introduce distorsione
lineare.
Il fattore di conversione potenza ricevutacorrente di uscita
del fotodiodo è pari a m g  r , in cui r è la responsività del
fotodiodo (0.5 Ampere/Watt) ed mg è il numero medio di
coppie elettrone/lacune generate a partire da un fotone
incidente ( per un diodo PIN, fino a 300 per un diodo a
valanga).
D.I.B.E.-Università di Genova
103
 iq t  è il RUMORE QUANTICO; il suo spettro di densità
2
di Pq  f   Fg mg q  r  wR potenza può assumersi uniforme (fino
a qualche GHz) pari a
 in t  rappresenta un rumore di natura termica;
il suo spettro di densità di potenza vale
Pn  f  
2 FkT0
R
Il filtro di ricezione H R  f 
ha lo scopo di eliminare il
rumore al di fuori della banda del segnale ed equalizzare il
comportamento della fibra dovuto al termine H D  f  .
Il calcolo del rapporto segnale/rumore verrà effettuato
all’uscita del filtro di ricezione nei due casi seguenti:
D.I.B.E.-Università di Genova
104
Due termini tengono conto del rumore:
eccitazione costante
w
s t   T (caso A)
GT
eccitazione pari ad una costante positiva più una
componente a valor medio nullo, funzione del segnale
utile:
w
s t   T 1  xt  , xt   1 (caso B)
2GT
In entrambi i casi wT indica il massimo valore della
potenza immessa nella fibra(Hc 2 costante con f se si va
nel range giusto (con M)).
ll segnale xt  si ritiene membro di un processo aleatorio
stazionario, di spettro di densità di potenza noto Px  f  .
D.I.B.E.-Università di Genova
105
Lo spettro di densità di potenza del segnale di eccitazione
vale:
wT2
0 ( f ) Delta di Dirac in f
Ps  f   2 u0  f  (caso A)
GT
wT2
u0  f   Px  f 
Ps  f  
4GT2
(caso B)
Il segnale all’ingresso del fotodiodo vale:
wR t   GT e
L
st   hd t   GT e
L
wR  GT e L ms  hd  d GT e L ms

 h  d  H 0  1  e
d
 st   h  d
d




lge 2 (
d
f 2
)
fT
, dato che
| f 0

Quindi:
ms  wT GT
(caso A)
ms  wT 2GT (caso B) Ipotesi di Ex(t) = 0
D.I.B.E.-Università di Genova
106
Dopo il filtro di ricezione si hanno tre contributi:
r t   rR t   rq t   rn t 
PrR  f   Ps  f GT2 e L  H D  f  mg2 r 2 R 2 H R  f 
2
2
2
u0  f  A


1
wT e 2L  mg2 r 2 R 2 H D  f   H R  f    1





B 
u
f

P
f
x
 4 0


4


 1 A
2

Prq  f   wT e L  Fg mg2 rqR 2  H R  f    1
 
 2 B
2
Prn  f   2 FkT0 R H R  f 
2
2
D.I.B.E.-Università di Genova
107
Per ottenere le potenze totali dei segnali in questione e
sufficiente integrare da - a + gli spettri di densità di
potenza ora calcolati.
Introduciamo le seguenti approssimazioni:
1. si trascura la distorsione della fibra [ H D  f   1 ];
2. si ritiene che H R  f  sia un passa-basso ideale con
frequenza di taglio pari alla banda B dei segnali:
1 f  B
HR  f   
0 altrove
Con queste approssimazioni:
2  2L
T
Pru  w e

 11  A
m r R 
Px B 

4
2
g
2
2
(comp.utile del segnale in uscita, nel caso B è solo quella
associata ad x(t), non al valor medio)
D.I.B.E.-Università di Genova
108

 A
1
2 L
2
2
1
Prq  wT e  Fg mg rqR  2 B
B 

2

Px  pot.x(t ) 
 P ( f )df
x

Prn  2 FkT0 R  2 B
Notazione: wR  wR wT , L  wT  exp L . Essendo HD(f)  1
Caso A:
wR2 mg2 r 2 R 2
Pru
SNRA 


Prq  Prn wR Fg mg2 rqR 2 2 B  2 FkT0 R  2 B
SNRq  wR
1
1
1

SNRq SNRn
a

bc
1
1
1

( a / b) ( a / c )
r
Fg q2B
D.I.B.E.-Università di Genova
109
migliora linearmente con la potenza luminosa ricevuta e
con la responsività del fotodiodo;
peggiora all’aumentare del fattore di rumore del
fotomoltiplicatore e della larghezza di banda.
 sarebbe meglio usare diodi PIN ( mg  1,Fg  1 ).
SNRqdB  92  wRdBm  10 lg 10 Fg  10 lg 10 BMHz
(r  0.5) r/29|dB
SNRn  wR2
mg2 r 2 R
4 FkT0 B

wR2 mg2 r 2 R
2 FkT0 R 2 B
migliora col quadrato della potenza luminosa e del guadagno
di fotomoltiplicazione(=mg);
D.I.B.E.-Università di Genova
110
sembrerebbe che un valore molto grande di R possa
annullare l’effetto del rumore termico, ma non si tiene in
conto della capacità di uscita C del diodo che, in
parallelo ad R, dà luogo ad un comportamento passabasso con frequenza di taglio 1 2RC . Si può compensare
tramite l’amplificatore di ingresso, facendo in modo che la
frequenza di taglio sia una frazione  abbastanza grande
della banda B:
1
1
 B  R 
2RC
2CB
Con R massima: SNRn 
wR2 mg2 r 2
4  2  CF  kT0 B 2
D.I.B.E.-Università di Genova

wR2 mg2 r 2
4  2Q  kT0 B 2
111
Q   CF ingloba tutti gli effetti del gruppo fotodiodo-amplificatore
agli effetti della valutazione del rumore termico. Supponendo
e Q  10 12 si ha: r  0.5
SNRndB  124  2wRdBm  20 lg 10 mg  20 lg 10 BMHz
L’andamento complessivo è mostrato nel grafico seguente:
D.I.B.E.-Università di Genova
112
I due SNR sono uguali per
4QkT0 ,
QkT
wR 0  B
SNRA0   2 0
qr
q
wR 0dBm  32  10 lg 10 BMHz
,
SNR
A0
 57dB
( Q  10 12 )
Se si impiegano diodi PIN e non si richiedono valori di rapporto
segnale/rumore molto elevati (wr non molto elevato), il rumore
prevalente è quello termico.
Per diodi a valanga, il valore ottimo da attribuire ad mg è quello per
cui è massimo il rapporto segnale/rumore complessivo (ottenibile
uguagliando a zero la derivata di SNRA rispetto ad mg):
w 
mgopt   R 0 
 awR 
1
2 1 a 
a  wR 
SNRA 


1 a  B 
1 2 a
1 a
, se wR 
r 



2q  4QkT0 
w r
SNRA  SNRq  R
B 2q
rq
per
1
wR 0
a
a
1 a
wR 
per
; mg opt  1 altrove
1
wR  wR 0
a
Condizione di uso dei
diodi a valanga
1
wR 0
a
D.I.B.E.-Università di Genova
113
12
Assumendo Q  10 , r  0.5 , a  0.2 :
SNRAdB  95  1.17 wRdBm  11.67 lg 10 BMHz
SNRAdB  92  wRdBm  10 lg 10 BMHz
per wR  5wR 0
per wR  5wR 0
Caso B: Il contributo del rumore quantico è dimezzato, mentre il
segnale utile è inferiore in quanto è pari al valore utilizzato in
precedenza moltiplicato per Px 4, in cui Px è la potenza del segnale
con la limitazione xt   1 .
Si verifica una riduzione della potenza utile:
PU dB  10 lg 10 Px  10 lg 10 4  PxdB  6
Quindi, rispetto al caso A:
SNRqdB   PxdB  6  3   PxdB  3 PBrq 
SNRndB   PxdB  6
PArn  PBrn  Prn
1
PArq
2
D.I.B.E.-Università di Genova
114
EQUALIZZAZIONE DI UN COLLEGAMENTO IN FIBRA OTTICA
Il problema si pone:
nel caso B esaminato in precedenza;
 quando la distorsione introdotta dalla fibra a causa di
H D  f  diventa sensibile;
quando la banda B del segnale diventa confrontabile con la
frequenza di taglio fT .


2B
SNR  SNRB wR   
P
 x


 B H o  f  Px  f df 


1
2
 H o  f  H  f  2 df 
D

B
2
in cui H o  f   H D  f  H R  f  è la FdT complessiva incontrata dal
segnale st  nel transito attraverso il collegamento, e SNRB wR  è il
rapporto segnale/rumore valutato nel precedente caso B.
D.I.B.E.-Università di Genova
115
Consideriamo il caso ideale in cui H R  f  è nullo fuori della banda
del segnale ed entro tale banda dà luogo ad una perfetta
equalizzazione ( H o  f   1 per f  B ):
HR f  
1
HD f 
 e lge 2 f
fT
2
per
f B
Supponendo Px  f  uniforme tra -B e B (zero altrove):
Px  f  
Px
2B
f B
per
si ricava che il rapporto segnale/rumore diminuisce di
2
1
B
1
e
B 0
 f 

2 lge 2
 fT 
e
2
 B 
 lge 2
 2 
 fT 
df
Il peggioramento in dB del rapporto segnale/rumore
dovuto alla presenza di dispersione della fibra è quindi:
 B
SNRD  6.02 
 fT 
2
 6dB se B  fT
piccolo se B << fT
D.I.B.E.-Università di Genova
116
Prestazioni di un collegamento in fibra ottica per
trasmissioni numeriche
È del tutto simile a quanto visto per il cavo coassiale:
 1
PE  1  erfcy
 L
, con
3R 2
y 
2L2  11   4
2
dove R2 è il rapporto segnale/rumore all’uscita della fibra.
Ipotesi:
impulso di dati rettangolare di durata TL;(approx utile per
calcolare Px)
2 livelli (L=2);
Px  1 [ xt  assume solo i valori +1 e -1].(caso più frequente)
Il rapporto segnale/rumore R2 è pari al valore ricavato nel caso A,
peggiorato delle quantità dovute all’effetto del rumore termico e
del rumore quantico con PxdB  0 .
D.I.B.E.-Università di Genova
117
Assumendo validi i dati utilizzati nel precedente
esempio e considerando anche il peggioramento
introdotto dalla dispersione della fibra equalizzata da
HR:
B
2
RdB
 95  1.17 wRdB  11.67 lg 10 BMHz  6  6.02 
 fT 
2
wRdBm  wT dBm  A0dB  Lkm
( A0dB
PEGGIORAMENTO MAX tra i 3dB di rum,q
e i 6dB di rum,n
= attenuazione kilometrica della fibra)
Per il dimensionamento, volendo ottenere PE  10 11 :
2
RdB
L 2
2
 ydB
 M dB  3  10 lg 10 1   4  24
avendo assunto   0.5 , M dB  6 .
D.I.B.E.-Università di Genova
118
2
B
 65  11.67 lg 10 BMHz  6.02   1.17 wRdBm
 fT 
dove B  fb 1    / 2 ,wRdBm  wT dBm  A0dB  Lkm
fT 
e
1
L2km L2km

Fm2 F2
2

L2km 
2  Lkm
 65  11.67 lg 10 BMHz  6.02 B  2  2   1.17 wRdBm

 Fm F 

B  f b 1    / 2;wRdBm  wT dBm  A0  Lkm

La limitazione in lunghezza della fibra ha origine da
attenuazione kilometrica (espressa dal termine A0dB );
dispersione della fibra (espressa dai termini Fm e F ).
D.I.B.E.-Università di Genova
119
Se pongo
Se invece
Fm  F  : A0  Lkm 
1
65  11.67 lg 10 BMHz   wT dBm
1.17

L2km L2km
1
A0  0 : 2  2 
65  11.67 lg 10 BMHz  1.17 wT dBm
2
Fm F
6.02 B
11
Lunghezza di tratta in km per PE  10 e per f b  140 Mbit/s;
il primo numero non tiene conto della dispersione, il secondo
non tiene conto dell’attenuazione della fibra.
Tab. v1/v2
1a finestra
2a finestra
2a finestra
3a finestra
3a finestra
(multimodo)
(multimodo)
(monomodo)
(multimodo)
(monomodo)
SLED
8.8/1.9
27/21.6
16.4/-
33.4/1.8
21.3/-
LASER
16.5/40
51.5/57.7
98.7/-
65/165
145/162
Risultato : L<min v1,v2
TdB dipende dalla sorgente luminosa (SLED,LASER)
D.I.B.E.-Università di Genova
120

Sistemi di trasmissione WDM
•Sono sistemi multicanale (Wavelength Division Multiplexing) che
trasmettono diverse lunghezze d’onda sulla stessa fibra.
•Esistono due categorie principali:
•Dense Wavelength Division Multiplexing (DWDM) con spaziatura
tra I canali di circa 100 GHz
•Coarse Wavelength Division Multiplexing (CWDM) con spaziatura
tra I canali di circa 1600 GHz
D.I.B.E.-Università di Genova
121
Sistemi di trasmissione DWDM
•I sistemi DWDM sono in grado di trasmettere fino a 40 canali da 10
Gbit/s ciascuno in banda C (1530-1565 nm) su distanze di oltre 100
Km senza rigenerazione intermedia.
•In banda C+L (1530-1625 nm) si possono invece trasmettere tra gli 80
ed I 160 canali a 10 Gbit/s su distanze di oltre 1000 Km.
•La capacità complessiva di un sistema DWDM su una singola coppia
di fibre è di oltre 1 Tbit/s (1 Terabit al secondo = 1000 Gbit/s)
Sistemi di trasmissione CWDM
•I sistemi DWDM sono in grado di trasmettere un numero limitato di
canali (circa 18) da 2.5 Gbit/s ciascuno su un’estesa gamma di
lunghezze d’onda (1260-1610 nm banda O+E+S+C+L)
•Le distanze massime consentite dal sistema sono limitate a circa 80
Km poichè non esistono ancora amplificatori con banda così larga
•Richiedono fibre senza picco di attenuazione da Ossidrile OH•Nonostante le limitazioni, sono molto utilizzati grazie al costo
sensibilmente inferiore rispetto ai sistemi DWDM
D.I.B.E.-Università di Genova
122