presentazione

Il tempo cosmico
Amedeo Balbi
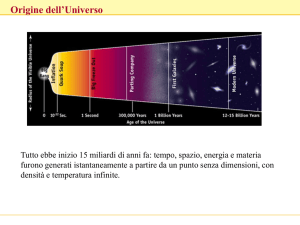
In principio…
QuickTime™ e un
decompressore
sono necessari per visualizzare quest'immagine.
Dorè, La creazione
Newton, De gravitatione (16661668):
lo spazio è independente dal
contenuto di materia, si estende
indefinitamente, e dura in eterno.
QuickTime™ e un
decompressore
sono necessari per visualizzare quest'immagine.
Bentley, con l’approvazione di
Newton, conclude che l’universo
contiene una distribuzione
uniforme e infinita di stelle,
“progettata” in stato di equilibrio.
Perché non una distribuzione
finita, stabilizzata dalla
meccanica? Le motivazioni di
Bentley erano essenzialmente
Tempo di collasso di una distribuzione sferica e uniforme di
punti, di massa totale M e raggio iniziale r0
Mm
r2
rÝ2  2GM(1/r 1/r0 )
mÝ
rÝ G

tC   r0 8GM
QuickTime™ e un
decompressore
sono necessari per visualizzare quest'immagine.

3

1/ 2
 3 32G 0 
1/ 2
Il risultato è indipendente dal
raggio iniziale del sistema.
Se ogni stella ha la stessa massa
del Sole, e la distanza media tra
stelle è 1 parsec, si ottiene un
tempo di collasso di circa 20
milioni di anni.
In realtà, anche il modello di universo di Bentley e Newton
(distribuzione uniforme e infinita di stelle) è problematico.
1. La risultante delle forze gravitazionali agenti su ogni massa
è infinita
2. La distribuzione di materia è in equilibrio instabile
Il tempo di instabilità gravitazionale, calcolato da Jeans, è
molto simile al tempo di collasso:
Tempo di instabilità
t J  1 4 G 0 
1/ 2
Tempo di collasso
tC  3 32G 0 
1/ 2
In generale, la scala di tempi caratteristica dei processi
guidati dalla gravità è:
1/ 2
t  1 G
Paradosso di Olbers (1823):
perché il cielo notturno è buio?
In un universo infinito, eterno e
statico, uniformemente pieno di
stelle, il cielo notturno dovrebbe
essere luminoso
(in ogni direzione si osserva
almeno una stella)
Gusci sferici concentrici:
dV  4 r 2dr
Numero di sorgenti in ogni guscio:
QuickTime™ e un
decompressore
sono necessari per visualizzare quest'immagine.

N  4r 2 ndr
Luminosità di ogni guscio:


L  N r 2  cost.
La luminosità del cielo
notturno dovrebbe essere
infinita!
Edgar Allan Poe
Eureka (1848)
“Se le stelle si susseguissero senza fine, lo sfondo
del cielo presenterebbe una luminosità uniforme,
come quella mostrata dalla Galassia, perché non
esisterebbe punto di quello sfondo in cui non brilli
una stella. L’unico modo, dunque, in cui potremmo
comprendere i vuoti osservati dai nostri telescopi in
tutte le direzioni, sarebbe di supporre che la
distanza dallo sfondo invisibile sia così immensa
che la luce non abbia ancora avuto il tempo di
raggiungerci.”
Universo infinito, ma non eterno
tempo
osservabile r=ct
orizzonte
Universo
spazio
Albert Einstein (1917)
Considerazioni cosmologiche sulla teoria della relatività generale
Assumendo che la distribuzione di materia nell’universo sia omogenea e
isotropo, Einstein tenta di ottenere una soluzione statica. Ma:
“In order to arrive at this consistent view, we admittedly had to introduce
an extension of the field equations of gravitation which is not justified”
G  g
8G
 4 T
c
costante
cosmologica
Analogo newtoniano:  2  4 G  
Soluzione statica per: 

 4G
 che, nei Principia, Newton aveva studiato anche una
È interessante
forma di legge gravitazionale del tipo:
F /m  CMr    3CM
Vesto Slipher (1922)
le linee spettrali delle
“nebulose” (galassie) appaiono
spostate verso la parte rossa
dello spettro elettromagnetico
Redshift z 




v
c
Interpretazione in termini di
effetto Doppler:
Le altre galassie si stanno
allontanando da noi
Henrietta Leavitt (1912)
Scoperta della relazione tra periodo e
luminosità delle stelle Cefeidi
“It is worthy of notice […] that the brighter
variables have longer periods.”
Hubble e Humason
(1929)
QuickTime™ e un
decompressore TIFF (Non compresso)
sono necessari per visualizzare quest'immagine.
“The results establish a
roughly linear relation
between velocities and
distance among nebulae.”
Legge di Hubble:
v  H0d
QuickTime™ e un
decompressore TIFF (Non compresso)
sono necessari per visualizzare quest'immagine.
Costante di Hubble, H0

QuickTime™ e un
decompressore
sono necessari per visualizzare quest'immagine.
La costante di Hubble introduce una scala di tempo in
cosmologia.
Tempo di Hubble:
t H 1 H0
Immaginiamo un momento iniziale per cui d=0. Qual è il
tempo t0 trascorso da allora?
Se il moto è uniforme:

d  vt0
v  d t0  t 0 1 H0  t H
Misure iniziali di Hubble:
H 0  500 km/s/Mpc
 t H  2 Gy
H0  72 km/s/Mpc

Misure attuali:

 t H  13.6 Gy
Ma, in generale, il tempo di Hubble non è l’età dell’universo.
Friedman e Lemaître mostrarono per primi che l’equazione di
Einstein prevede modelli di universo omogenei e isotropi in
espansione.
A posteriori, si mostra (Milne e Mc Crea) che la dinamica di
tali modelli è analoga a quella di una distribuzione di materia
sferica e omogenea soggetta alla propria gravità.
Fattore di scala:
a  r r0
aÝ2 8
k
Eq. di Friedman:   
G  2
a 
3
a

In questa analogia k è una costante di integrazione. In
relatività generale essa è legata alla curvatura spaziale
dell’universo.

Nell’analogia con la sfera autogravitante la costante k è
legata all’energia meccanica del sistema

I casi con energia positiva,
negativa o nulla (k<0, k>0,
k=0) corrispondono a tre
diversi comportamenti
dinamici dell’espansione.
 T  U  E  cost.  2k mr02
fattore di scala
1
1
2 2
Ý
T  mrÝ2  mrÝ
0 a
2
2
GMm
4G
U 

mr02 a 2
r
3
E>0
E=0
E<0
tempo
La velocità di espansione dell’universo varia con il tempo e dipende dal
modello.
aÝ2 8
k
G  2
  
a 
3
a
k 0
(critico)
k 0

8G0 
12
a da  
 dt
 3  
12
 a  t2 3
L’universo si espande per
sempre, ma la velocità di
espansione tende a zero.

k 0
(legato, “chiuso”)
8
3
8
0
3
aÝ2 
G 0
k
a
G 0
k
amax

Il moto si arresta e si
inverte ad un tempo
finito:
amax 
8 G0
3 k
(slegato, “aperto”)

aÝ2  k  0
La velocità di espansione
è sempre positiva, il moto
non si arresta mai.
La legge di Hubble vale per ogni tempo, a patto di definire un
parametro di Hubble dipendente dal tempo:
Quindi, la scala di tempo caratteristica dell’espansione (il
tempo di Hubble) varia col tempo:
Il tempo di Hubble
non è l’età
dell’universo
tH
t0
oggi
fattore di scala
(k=0)
tempo
Il tempo di Hubble scandisce il ticchettìo del metronomo cosmico
prestissimo t~10-35s
Grande unificazione, inflazione
presto
t~10-12s
Unificazione elettro-debole
vivace
t~10-7s
Transizione quark-adroni
allegro
t~100 s
Sintesi dei nuclei leggeri
moderato
t~300 000 anni
Formazione dell’idrogeno
andante
t~10 000 anni
Epoca della materia
largo
t~13.7 miliardi di anni
Oggi
Non tutte le epoche sono uguali
L’introduzione della costante cosmologica nell’equazione di
Friedman permette di realizzare un modello in cui
l’espansione avviene sempre allo stesso ritmo:
Modello di De Sitter, espansione esponenziale:
Questo tipo di andamento, senza un’origine temporale, era
ipotizzato nel modello dello stato stazionario, ormai
abbandonato.
Nel modello stazionario, la coincidenza tra il tempo di Hubble
misurato e il tempo caratteristico di vita di una stella (t~10
I tempi dell’evoluzione stellare
Diagramma colore-magnitudine per
40 mila stelle vicine al Sole
Gli ammassi globulari
contengono milioni di
stelle che si sono
formate nella stessa
epoca e sono molto
antiche.
Possiamo usarli per
stimare l’età
dell’universo.
M5: 2106 M, distanza 0.8 kpc
Diagramma colore magnitudine dell’ammasso M5
Ramo orizzontale
Magnitudine
Ramo delle
giganti rosse
Punto del “turnoff”
Colore
Sequenza
principale
Il punto in cui si interrompe la sequenza principale indica l’età
dell’ammasso.
Le età degli ammassi globulari più antichi sono dell’ordine di 12 miliardi di
Le nane bianche sono oggetti densissimi, lo stadio finale di stelle di
massa simile a quella del Sole, compresse in un volume inferiore a quello
terrestre.
L’unica sorgente di
energia nelle nane
bianche è il loro calore
residuo.
QuickTime™ e un
decompressore
sono necessari per visualizzare quest'immagine.
Dalla temperatura delle
nane bianche si ottiene
quindi una stima della
loro età.
Le nane bianche più
deboli sono le più antiche,
e possono essere usate
La nebulosa dell’Elica per stimare l’età
dell’universo.
Le età delle nane bianche più deboli sono dell’ordine di 12 miliardi di anni.
Dal punto di vista teorico, per calcolare l’età dell’universo
bisogna integrare l’equazione di Friedman.
Un caso semplice. Universo di Einstein - De Sitter, k=0.
Densità critica:
La radiazione di fondo nelle microonde:
lo stato dell’universo 380 000 anni dopo il big
bang
http://lambda.gsfc.nasa.gov/product/map/current/google_sky/
QuickTime™ e un
decompressore
sono necessari per visualizzare quest'immagine.
La composizione del cosmo è oggi nota con grande
precisione.
Con questi parametri, si ottiene un’età dell’universo di 13.7
miliardi di anni, del tutto in accordo con quella degli altri
indicatori.
Ma le cose sono più complicate.
Che significato fisico ha il tempo t=0?
Come si curano le condizioni di energia e densità
infinità del big bang?
a
Singolarità
t
Agostino, Confessioni, Libro XI
“Ecco come rispondo a chi domanda che
cosa faceva Dio prima di fare il cielo e la
terra. Non come fece quel tale che eluse
con una battuta di spirito l'aggressività
della domanda, rispondendo, dicono:
"Preparava la Geenna per chi indaga gli
abissi". Ridere non basta per capire. No,
non rispondo a questo modo: preferirei
allora una risposta come "Quello che non
so, non lo so", che almeno risparmia la
facile ironia per chi solleva una questione
profonda e il plauso per chi dà una
risposta falsa.”
Inflazione
Una fase di espansione esponenziale, trainata dall’energia
dello spazio vuoto (costante cosmologica).
a
t
Inflazione eterna: un insieme di universi che si autoriproducono
Modello
ciclico
(ekpyrotico)