Nome - Cnr

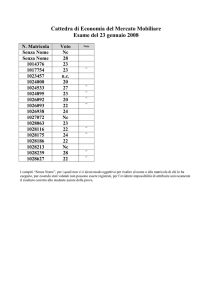
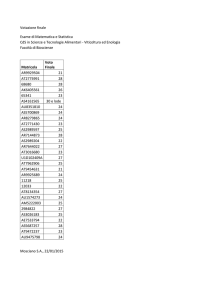
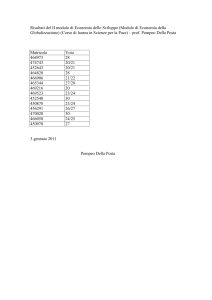
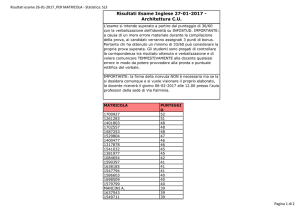
Modello relazionale
Il Modello Relazionale
• Il modello relazionale dei dati, proposto nel 1970 ed adottato nei
sistemi commerciali a partire dal 1978, si è diffuso rapidamente
tanto sui sistemi grandi quanto sugli elaboratori personali.
• Definizione: I meccanismi per definire database con il modello
relazionale sono l’ennupla (o record) e la relazione (o tabella):
– una relazione R è definita da un insieme finito di coppie
(campi) della forma T = (A1: T1, A2:T2,…, Ak:Tk) dove gli Ai
sono detti attributi e i Ti sono tipi elementari
– lo schema di una base di dati è un insieme di relazione
Ri(Ti);
– un’istanza di una relazione R(T) è un insieme finito di
ennuple di tipo T, cioe di oggetti della forma (A1:v1, A:v2, …,
Ak:vk) dove i vi sono di tipo Ti
Modello relazionale
Esempio: relazione Studenti
Schema Relazione
Studenti(Nome: string, Matricola: string, Provincia: string, AnnoNascita:int)
attributo
Istanza di Studenti
ennupla
Nome
Matricola
Provincia AnnoNascita
Isaia
171523
PI
1980
Rossi
167459
LU
1975
Bianchi 179856
LI
1078
Bonini
PI
1980
175649
Valore
di attributo
Per semplicità una relazione si rappresenta come una tabella le cui
colonne rappresentano gli attributi della relazione e le righe le ennuple
della relazione.
Modello relazionale
Chiavi
• Chiave
Un insieme di campi di una tabella è una chiave se
per ogni istanza di tale tabella non esistono due
record che coincidano su tutti i valori di tali campi.
• Chiave primaria: una delle chiavi, in genere la più
corta
– Esempio:
(Matricola) e (Nome,Indirizzo)
sono chiavi in
Studenti(Matricola: Int, Nome: String, Indirizzo: String)
Modello relazionale
Associazioni
• Associazione tra ennuple
– rappresentata attraverso i valori di un insieme di
attributi (chiave esterna), che assume come valori
quelli della chiave primaria di un’altra relazione.
• Es.
Studenti
Nome
Matricola
Provincia
AnnoNascita
Isaia
171523
PI
1980
Esami
Materia
Candidato
Data
Voto
BD
171523
12/01/01
29
Modello relazionale
Associazione: esempio
Studenti(Nome: string, Matricola: string, Provincia: string,
AnnoNascita:int)
Esami(Materia: string, Candidato*: string, Data: string, Voto: int)
Studenti
Nome Matricola Provincia AnnoNascita
Studenti
Nome
Matricola
Provincia AnnoNascita
Isaia
171523
PI
1980
Rossi
167459
LU
1975
Bianchi 179856
LI
1078
Bonini
PI
1980
175649
Esami
Materia
Esami
Materia
Data
Voto
Voto
BD
Candidato Data
*171523
12/01/01
BD
167459
15/01/01
30
FP
179856
13/02/01
30
BD
175649
15/01/01
25
LMM
171523
11/02/01
18
28
Modello relazionale
Schema grafico relazionale
Studenti(Nome: string, Matricola: string, Provincia:
string, AnnoNascita:int)
Esami(Materia: string, Candidato*: string, Data: string,
Voto: int)
Nome
Materia
Candidato*
Matricola
Studenti
Esami
Provincia
Data
AnnoNascita
Voto
Legenda:
A
B
In B c’è una chiave
esterna per A
Modello relazionale
Esempio: altre soluzioni 1/2
Studenti(Nome: string, Matricola: string, Provincia:
string, AnnoNascita:int, Esame*:int)
Esami(Codice :int, Materia: string, Data: string, Voto:
int)
Nome
Matricola
Esame*
Materia
Codice
Studenti
Esami
Provincia
Data
AnnoNascita
Voto
Modello relazionale
Esempio: altre soluzioni 2/2
Studenti(Nome: string, Matricola: string, Provincia:
string, AnnoNascita:int)
Esami(Codice :int, Materia: string, Data: string, Voto:
int)
StudentiEsami(Esame*: int, Candidato*: string)
Nome
Materia
Codice
Matricola
Studenti
Esami
Provincia
Data
AnnoNascita
Voto
StudentiEsami
Candidato*
Esame*
Conversione ER-relazionale
Trasf. di schemi ER in relazionali
• Il modello relazionale non si presta alla
modellazione concettuale per la sua
povertà espressiva
– Attributi con tipi elementari
– Associazioni con chiavi esterne, (1:1) o
(0:n)?
• Quindi:
– Si modella con diagrammi ER
– Regole di trasformazione da ER a
formalismo grafico relazionale
Conversione ER-relazionale
Passi di trasformazione
Passi di trasformazione:
–
–
–
–
–
–
Trasf. associazioni 1:1 e 0:n
Trasf. associazioni n:n
Trasf. Gerarchie di inclusione
Identificazione chiavi primarie
Trasf. attributi multivalore
Appiattimento attributi composti
Scopo:
–
–
–
–
Rappresentare le stesse informazioni
Minimizzare la ridondanza
Schema comprensibile
Evitare sprechi di memoria
Conversione ER-relazionale
Associazioni 0:n
Nome
Materia
Data
Voto
Matricola
Esami
Studenti
Provincia
AnnoNascita
Materia
Candidato*
Nome
Matricola
Esami
Studenti
Data
Provincia
Voto
AnnoNascita
Regola
Chiave esterna aggiunta alla tabella con associazione
univoca
Conversione ER-relazionale
Associazioni 1:1
Nome
idFacolta
Indirizzo
DirettaDa
Facolta
DirettoreDi
Professori
Nome
Nome
idFacolta
Direttore*
Indirizzo
idProfessore
Facolta
Professori
Provincia
AnnoNascita
Regola
Chiave esterna aggiunta a una qualsiasi delle due
tabelle coinvolte (precedenza al vincolo di totalità)
Conversione ER-relazionale
Associazioni unarie
Nome
compagnoDi
idPersona
Provincia
Persone
AnnoNascita
Nome
idPersona
Compagno*
Persone
Provincia
AnnoNascita
Regola
Si aggiunge una chiave esterna alla tabella stessa
Conversione ER-relazionale
Associazioni n:n
Nome
idConto
Persone
CCorrenti
idPersona
Saldo
idPersona*
idConto*
Nome
idConto
Persone
idPersona
Persone-CC
CCorrenti
Saldo
Regola
Si aggiunge una terza tabella che contiene le chiavi
esterne relative alle due tabelle coinvolte.
Conversione ER-relazionale
Associazione con proprietà
Data
Titolo
idLibro
Nome
Libri
Autore
Utenti
prestatoA
libriInPrestito
Titolo
Utente*
Autore
idUtente
Nome
Libri
Utenti
idUtente
Data
idLibro
Libro* Data Utente*
Titolo
Autore
Libri
Prestiti
Utenti
idLibro
Regola
Attributi aggiunti alla tabella con chiave esterna,
oppure ad una terza tabella con due chiavi esterne
Nome
idUtente
Conversione ER-relazionale
Esempio di conversione
Editori
Editori
Libri
Prestiti
Autori
Utenti
Libri
Prestiti
Autori-Libri
Autori
Utenti
Conversione ER-relazionale
Attributi multivalore
Persone
Persone
LingueParlate
Lingua
Persone
LingueParlate
Lingua
LingueParlate
Persone
LingueParlate
Lingue
Conversione ER-relazionale
Le sottoclassi
Persone
Studenti
[ nome: string
Diventa:
età: int
codice: int ]
[ corsoDiLaurea: string
matricola: int ]
Oppure:
Persone
Persone
Studenti
Oppure:
( nome: string
età: int
codice: int
corsoDiLaurea:
optional string
matricola: optional int )
Persone
Studenti
( Nome: string
età: int
codice: int )
( codice*: int
corsoDiLaurea: string
matricola: int )
( Nome: string
età: int
codice: int )
( codice: int
Nome: string
età: int
corsoDiLaurea: string
matricola: int )
Conversione ER-relazionale
Le sottoclassi (cont.)
Persone
AttrM
AttrM optional
AttrF optional
Maschi
Persone
AttrM con chiave
esterna ChP
Maschi
AttrP con
chiave ChP
Persone
AttrF con chiave
esterna ChP
Femmine
AttrP con chiave ChP
Femmine
AttrF
AttrP con chiave ChP
Maschi
AttrP con
chiave ChP
e AttrM
Femmine
AttrP con
chiave ChP
e AttrF
Conversione ER-relazionale
Criteri di scelta
• Numero di attributi delle sottoclassi
• Tipo di operazioni
– Riguardano tutte le informazioni di
elementi di una sottoclasse?
– Riguardano la visita di tutti gli elementi
della superclasse?
Linguaggi relazionali
Linguaggi relazionali
Per il modello relazionale sono stati definiti due
principali linguaggi che sono stati poi usati per
definire e implementare il linguaggio SQL dei DBMS.
Algebra relazionale
insieme di operatori su relazioni che danno come
risultato relazioni. Non si usa come linguaggio di
interrogazione dei DBMS ma come rappresentazione
interna delle interrogazioni.
Calcolo relazionale
linguaggio dichiarativo di tipo logico dal quale è stato
derivato l'SQL.
Linguaggi relazionali
Algebra relazionale
Notazione
ReS
relazioni
t, s
ennuple
A,B,C
attributi
X,Y,Z
insiemi di attributi
Operatori di base
• Proiezione
• Restrizione
• Ridenominazione
• Prodotto
• Giunzione
Linguaggi relazionali
Proiezione
Proiezione (): elimina gli attributi che non sono nella
lista di proiezione
 A1...An (R)
Qual è il tipo del risultato?
Se R ha n elementi quanti ne ha il risultato?
Linguaggi relazionali
Esempi di proiezione
Studenti
Nome
Matricola
Provincia AnnoNascita
Isaia
171523
PI
1980
Rossi
167459
LU
1975
Bianch
iBonini
179856
LI
1078
175649
PI
1980
 Nome, Matricola (Studenti)
 Nome (Studenti)
Nome
Matricola
Nome
Isaia
171523
Isaia
Rossi
167459
Rossi
Bianchi
179856
Bianchi
Bonini
175649
Bonini
Linguaggi relazionali
Restrizione
Restrizione (selezione) (): seleziona le ennuple della
relazione che soddisfano la condizione.
Condizione (R)
Qual è il tipo del risultato?
Se R ha n elementi quanti ne ha il risultato?
Linguaggi relazionali
Esempio di restrizione
Studenti
Nome
Matricola
Provincia AnnoNascita
Isaia
171523
PI
1980
Rossi
167459
LU
1975
Bianchi
179856
LI
1078
Bonini
175649
PI
1980
 AnnoNascita<1979 (Studenti)
Nome
Matricola
Provincia AnnoNascita
Rossi
167459
LU
1975
LI
1078
Bianchi 179856
Linguaggi relazionali
Es. di composizione di operatori
Studenti
Nome
Matricola
Provincia AnnoNascita
Isaia
171523
PI
1980
Rossi
167459
LU
1975
Bianchi
179856
LI
1078
Bonini
175649
PI
1980
Il numero di matricola degli studenti nati prima del 1979
 Matricola( AnnoNascita<1979 (Studenti) )
Matricola
167459
179856
Linguaggi relazionali
Prodotto e ridenominazione
Prodotto (): l'operatore ha due argomenti R e S con attributi distinti e
il risultato è una relazione con elementi ottenuti concatenando ogni
ennupla di R con tutte quelle di S.
a
A
a1
A1
a2
A2
b
B
b1
B1
b2
B2
b3
B3
a
A
b
B
a1
a1
a1
a2
a2
a2
A1
A1
A1
A2
A2
A2
b1
b2
b3
b1
b2
b3
B1
B2
B3
B1
B2
B3
Ridenominazione (): cambia il nome di un attributo di una relazione
A  B (R)
Linguaggi relazionali
Giunzione
Giunzione naturale (
)
R(ZX) e S(YX)
R
S = { t | t[XY]R e t[ZX]S }
A
B
a
A
A1
B1
a1
A1
A3
B2
a2
A2
A1
B3
A2
B3
Giunzione esplicita
R
a
a1
a1
a2
S
R.A = S.B
A
A1
A1
A2
B
B1
B3
B3
Linguaggi relazionali
Esempi di giunzione 1/4
Trovare i nomi degli studenti che hanno passato un esame con
voto inferiore a 28
Studenti
Nome
Matricola
Provincia AnnoNascita
Isaia
171523
PI
1980
Rossi
167459
LU
1975
Bianchi 179856
LI
1978
Bonini
PI
1980
175649
Esami
Materia
Voto
BD
Candidato Data
*171523
12/01/01
BD
167459
15/01/01
30
FP
179856
13/02/01
30
BD
175649
15/01/01
25
LMM
171523
11/02/01
18
28
Linguaggi relazionali
Esempi di giunzione 2/4
 Nome( Voto<28 (Studenti
Esami))
Matricola = Candidato
Nome
Matricola
Provincia
AnnoNascita
Materia
Candidato
Data
Voto
Isaia
171523
PI
1980
BD
171523
12/01/01 28
Isaia
171523
PI
1980
LMM
171523
11/02/01
Rossi
167459
LU
1975
BD
167459
15/01/01 30
Bianchi
179856
LI
1978
FP
179856
13/02/01 30
Bonini
175649
PI
1980
BD
175649
15/01/01 25
18
Linguaggi relazionali
Esempi di giunzione 3/4
 Nome( Voto<28 (Studenti
Esami))
Matricola = Candidato
Nome
Matricola
Provincia
AnnoNascita
Materia
Candidato
Data
Voto
Isaia
171523
PI
1980
LMM
171523
11/02/01
18
Bonini
175649
PI
1980
BD
175649
15/01/01 25
Linguaggi relazionali
Esempi di giunzione 4/4
 Nome( Voto<28 (Studenti
Esami))
Matricola = Candidato
Nome
Isaia
Bonini
Linguaggi relazionali
Trasformazioni algebriche
• Basate su regole di equivalenza fra espressione algebriche
• Consentono di scegliere diversi ordini di join e di anticipare proiezioni e
restrizioni.
• Consideriamo la relazione R(A, B, C, D):
A (AB (ABC (R)))  A(R)
C1(C2(C3(R)  C1  C2  C3(R)
C1  C2(E1  E2)  C1 (E1)  C2 (E2)
R (S  T)  (R  S)  T
(R  S)  (S  R)
• Ottimizzazione algebrica: anticipazione delle proiezioni e delle
restrizioni rispetto al prodotto per ridurre la dimensione dei risultati
intermedi
Linguaggi relazionali
Alberi logici e trasformazioni algebriche
Consideriamo le relazioni R(A, B, C, D) e S(E, F, G) e
l'espressione:
A,F(A=100 and F > 5 and
A=E
(R x S))
A,F
A,F
A=E
A=100
F>5
A=E


R
A
E, F
A=100
F>5
S
R
S
Extra su Algebra Relazionale
Linguaggi relazionali
Algebra relazionale: (cont.)
Unione (): l'operatore ha due argomenti R e S dello stesso tipo e
il risultato è una relazione ottenuta facendo l'unione delle
ennuple di R con quelle di S.
RS
Differenza (-): l'operatore ha due argomenti R e S dello stesso tipo
e il risultato è una relazione contenente le ennuple di R non
presenti in S.
R - S = { t | tR e tS }
Qual è il tipo del risultato? Se R e S hanno n elementi quanti ne ha
il risultato?
Se t1 è un'ennupla non in R , allora
R = (R  {t1}) - {t1})
Linguaggi relazionali
Algebra relazionale: (cont.)
Semi-giunzione ( )
R(ZX) e S(YX)
R
A
B
A1
B1
A3
B2
A1
B3
A2
B3
S = { t R | t[X] X(S) }
a
A
A
B
a1
A1
A1
B1
a2
A2
A1
B3
a2
A4
A2
B3
Linguaggi relazionali
Algebra relazionale: (cont.)
Operatori derivati
Intersezione ()
R  S = { t | t R e t S }
Divisione ( \ )
R \ S = { t | {t}  S  R} vale che (R  S)\S = R
a
A
b
B
a1
a1
a1
a2
a2
a2
A1
A1
A1
A2
A2
A2
b1
b2
b3
b1
b2
b3
B1
B2
B3
B1
B2
B3
b
B
b1
B1
b2
B2
b3
B3
a
A
a1
A1
a2
A2