Array

Corso di Calcolatori Elettronici
APPUNTI SUL LINGUAGGIO C
Esercitazione I
Esercizi di base
Esercizio: Scrivere un programma per calcolare il massimo tra 10
numeri forniti dall’utente.
n1
a
b
ni
max
n2
n3
n10
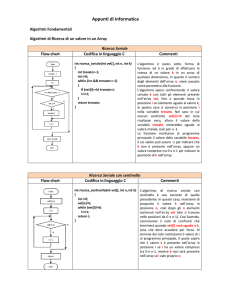
Pseudocodifica
► scriviamo una procedura per calcolare il massimo tra due numeri
MAX(a,b)
if a>b then massimo ← a
else massimo ← b
return massimo
► scriviamo una procedura che calcola il massimo tra 10 numeri
MAXtot()
i ← 2
Leggi(a)
Leggi(b)
massimo ← MAX(a,b)
while i < 10
do Leggi(a)
massimo ← MAX(massimo,a);
i ←
i + 1
return massimo
Pseudocodifica
► algoritmo principale
begin
massimo ← Maxtot()
Stampa(massimo)
end
Programma C
#include <stdio.h>
int MAX(int a, int b) {
int massimo;
if (a>b) massimo=a;
else massimo=b;
return massimo;
}
int MAXtot() {
int a, i=2, massimo;
scanf("%d", &a); scanf("%d", &massimo); massimo = MAX(a,massimo);
while (i<10) {
printf("Inserire un numero:"); scanf("%d", &a);
Massimo = MAX(massimo,a); i++; return massimo;
}
main() {
printf("Il numero massimo inserito e’: %d\n", MAXtot());
}
Array
Esercizio: Data una lista di N numeri (un array di N elementi) stampare il
minimo e il massimo elemento tra gli N forniti da input.
Oss. N sia una costante (per esempio 15).
Pseudocodifica
► scriviamo una procedura per calcolare il massimo in un vettore
MAX(vet)
max ← vet[0]
for i ← 1 to 15
do if vet[i] > max then max = vet[i]
return max
► scriviamo una procedura per calcolare il minimo in un vettore
MIN(vet)
min ← vet[0]
for i ← 1 to 15
do if vet[i] < min then min = vet[i]
return min
Pseudocodifica
► algoritmo principale
begin
Leggi(vet)
massimo ← MAX(vet)
minimo ← MIN(vet)
Stampa(minimo)
Stampa(massimo)
end
Array
include <stdio.h>;
#define N 15 /* è noto a tutti che la dimensione
del vettore è N */
int minimo (int vet[]) {
int i, min;
min = vet[0];
for (i = 1; i<N; i ++)
if (vet[i]<min) min = vet[i];
return min;
}
int massimo (int vet[]) {
int i, max;
max = vet[0];
for (i = 1; i<N; i ++)
if (vet[i]>max) max = vet[i];
return max;
}
Array
main () {
int i, a[N];
printf ("Scrivi %d numeri interi\n", N);
for (i = 0; i<N; i++)
scanf ("%d", &a[i]);
printf ("Il minimo vale %d e il massimo è %d\n", minimo(a),
massimo(a));
}
Array
Dati N valori interi forniti in ordine qualunque, stampare in
uscita l'elenco dei valori dati in ordine crescente.
Oss. N sia una costante (per esempio 15).
Vettore di elementi di un certo tipo, sul quale è definita una relazione
d’ordine totale :
– Selection sort, o ordinamento per minimi successivi:
– Ad ogni passo seleziona il minimo nel vettore e lo pone nella
prima posizione, richiamandosi ed escludendo dal vettore il primo
elemento.
Array
Primo livello di specifica:
– leggi gli elementi
– ordina il vettore
– stampa il vettore ordinato
• Secondo livello di specifica per l’ordinamento
while (<il vettore ha più di una componente>)
{ <individua il minimo nel vettore corrente in posizione posmin>
<scambia se necessario il primo elemento del vettore corrente con
quello in posizione posmin >
<considera come vettore corrente quello precedente tolto il primo
elemento>
}
Array
posmin
[0]
[1]
[2]
[3]
2
5
1
-1
posmin
[0]
[1]
[2]
[3]
[0]
[1]
[2]
[3]
-1
5
1
2
-1
5
1
2
Vettore corrente
Pseudocodifica
► scriviamo una procedura per ordinare un vettore tramite l’insertion sort
SORT(vet)
for j ← 0 to lenght(vet)
do posmin ← j
min ← vet[j]
► mi calcolo posmin
for i ← j to lenght(vet)
do if vet[i] < min then min ← vet[i]
posmin ← i
► verifico se il posmin è cambiato e quindi scambio
if posmin ≠ j then vet[posmin] ← vet[j]
vet[j] ← min
Pseudocodifica
► algoritmo principale
begin
Leggi(vet)
SORT(vet)
Stampa(vet)
end
Array
#include <stdio.h>
#define N 15
void leggi(int a[]) {
int i;
printf ("Scrivi %d interi\n", N);
for (i = 0; i < N; i++)
scanf ("%d", &a[i]);
}
void scrivi(int a[]) {
int i;
printf ("Vettore ordinato:\n");
for (i = 0; i < N; i++)
printf ("%d \t", a[i]);
}
Array
void sort (int vet[]) {
int j, i, posmin, min;
for (j=0; j < N; j++) {
posmin=j;
min = vet[j];
for (i=j+1;i<N; i++)
if (vet[i]<min) {
min=vet[i];
posmin=i;
}
if (posmin != j) { /*scambio */
vet[posmin]=vet[j];
vet[j]= min;
}
}
}
Array
main () {
int i, a[N];
leggi(a);
sort(a);
scrivi(a);
}
Array
Dati N valori interi forniti in ordine qualunque, stampare in
uscita l'elenco dei valori dati in ordine crescente.
Oss. N sia una costante (per esempio 15).
Vettore di elementi di un certo tipo, sul quale è definita una relazione
d’ordine totale :
– Merge Sort
Merge Sort
dividi
fondi
Merge Sort
• Assumiamo di avere un vettore A
• Indichiamo con p e r gli indici di estremo (primo e
ultima posizione)
• q rappresenta l’indice di pivot per dividere una
sequenza
• p<q<r
• A[p..q] e A[q+1..r] sono ordinati
– MERGE(A,p,q,r) per fondere
– MERGE-SORT(A,p,r) per ordinare
► scriviamo la procedura di fusione
MERGE(A,p,q,r)
i ← p
j ← q+1
k ← 1
while i <= q and j <= r
do if A[i] <= A[j] then APP[k] ← A[i]
i ← i + 1
else APP[k] ← A[j]
j ← j + 1
k ← k + 1
if i = q+1 then for i ← j to r
do APP[k] ← A[i]
k ← k+1
else for j ← i to q
do APP[k] ← A[j]
k ← k+1
k ← 1
for i ← p to r
do A[i] ← APP[k]
k ← k + 1
► scriviamo la procedura di ordinamento
MERGE-SORT(A,p,r)
if p < r then q ← (p+r)/2
MERGE-SORT(A,p,q)
MERGE-SORT(A,q+1,r)
MERGE(A,p,q,r)
► scriviamo il blocco principale
begin
Leggi(vet)
MERGE-SORT(vet,1,lenght(vet))
Stampa(vet)
end
Array
#include <stdio.h>
#define N 15
void leggi(int a[]) {
int i;
printf ("Scrivi %d interi\n", N);
for (i = 0; i < N; i++)
scanf ("%d", &a[i]);
}
void scrivi(int a[]) {
int i;
printf ("Vettore ordinato:\n");
for (i = 0; i < N; i++)
printf ("%d \t", a[i]);
}
void Merge(int A[], int iniziale, int mediano, int finale) {
/* Fonde i due sottovettori ordinati di A da iniziale a mediano e
da mediano+1 a finale in un unico sottovettore ordinato. */
int B[100]; /* vettore di appoggio */
int primo, secondo, appoggio, da_copiare;
primo = iniziale;
secondo = mediano + 1;
appoggio = iniziale;
while (primo <= mediano && secondo <= finale) {
if (A[primo] <= A[secondo]) {
B[appoggio] = A[primo]; primo++;
}
else {
B[appoggio] = A[secondo]; secondo++;
}
appoggio++;
}
if (secondo > finale)
/* e‘ finito prima il secondo sottovettore; copia da A in B tutti
gli elementi del primo sottovettore fino a mediano */
for (da_copiare = primo; da_copiare <= mediano; da_copiare++) {
B[appoggio] = A[da_copiare];
appoggio++;
}
else
/* e‘ finito prima il primo sottovettore copia da A in B tutti
gli elementi del secondo sottovettore fino a finale */
for (da_copiare = secondo; da_copiare <= finale; da_copiare++) {
B[appoggio] = A[da_copiare];
appoggio++;
}
/* ricopia tutti gli elementi da iniziale a finale da B ad A */
for (da_copiare = iniziale; da_copiare <= finale; da_copiare++)
A[da_copiare] = B[da_copiare];
} /* MergeVettore */
void MergeSort(int A[], int iniziale, int finale) {
/* Ordina gli elementi del vettore A di indice compreso tra iniziale e
finale usando l’algoritmo di ordinamento per fusione. */
int mediano;
if (iniziale < finale) { /* l’intervallo da iniziale a finale,
estremi inclusi comprende almeno
due elementi */
mediano = (iniziale + finale) / 2;
MergeSort(A, iniziale, mediano);
MergeSort(A, mediano+1, finale);
Merge(A, iniziale, mediano, finale);
}
} /* MergeRicorsivo */
main(){
/* Ordina i primi n elementi del vettore A usando l’algoritmo
di ordinamento per fusione. */
int A[100];
leggi(A);
MergeSort(A, 0, N-1);
scrivi(A);
} /* MergeSort */
Array
Dati N valori interi forniti in ordine qualunque, stampare in
uscita l'elenco dei valori dati in ordine crescente.
Oss. N sia una costante (per esempio 15).
Vettore di elementi di un certo tipo, sul quale è definita una relazione
d’ordine parziale :
– Heap Sort
Heap
Un Heap è un albero bilanciato rappresentato mediante un array.
Ad ogni nodo dell’albero è associato un indice
1
:
2
3
4
8
5
9
6
10
8 3 5 9 1 4 7 6 0 2
7
Heap
Un Heap è una struttura dati composta da un array che possiamo considerare
come un albero binario quasi completo. Ad ogni nodo dell’albero è associato
un indice
1
:
9
2
8
4
6
8
5
9
0
5
2
3
6
7
4
10
1
9 8 7 6 2 4 5 5 0 1
7
5
Heap in C
Utiliziamo una convenzione:
•
In posizione [0] indichiamo il numero di elementi dell’Heap (hp)
•
In posizione [N-1] indichiamo la lunghezza N dell’array
•
PARENT(i), LEFT(i) e RIGHT(i) restituiscono gli indici del padre, figlio
sinistro, figlio destro del nodo in posizione i.
1
:
9
2
8
4
6
8
5
9
0
5
2
3
6
4
7
7
5
10
1
10 9 8 7 6 2 4 5 5 0 1 .. 99
► scriviamo le procedure di navigazione dell’HEAP
PARENT(i)
return i/2
LEFT(i)
return 2i
RIGHT(i)
return 2i+1
Heapify
Due Tipi di HEAP
•
MAX-HEAP: A[PARENT(i)] > A[i]
•
MIN-HEAP: A[PARENT(i)] < A[i]
Si vuole conservare tale proprietà di HEAP.
► Scriviamo la procedura di MAX-HEAPIFY
MAX-HEAPIFY(A,i)
l ← LEFT(i)
r ← RIGHT(i)
if l < A[0] and A[l] > A[i] then massimo ← l
else massimo ← i
if r < A[0] and A[r] > A[massimo] then massimo ← r
if massimo ≠ i then “scambia A[i] con A[massimo]”
MAX-HEAPIFY(A,massimo)
► Dato un Array qualsiasi vogliamo convertirlo in un MAX-HEAP
BUILD-MAXHEAP(A)
A[0] ← lenght(A)
for i ← lenght(A)/2 downto 1
do MAX-HEAPIFY(A,i)
Proprietà che le foglie in un heap partono dall’indice n/2,
con n numero di nodi
► Dato un Array qualsiasi vogliamo ordinarlo con l’HEAP-SORT
HEAPSORT(A)
BUILD-MAXHEAP(A)
for i ← lenght(A) downto 2
do “scambia A[1] con A[i]”
A[0] ← A[0] - 1
MAX-HEAPIFY(A,1)
#include <stdio.h>
#define N 100
// PARENT(i), LEFT(i), RIGHT(i) e scambia
int PARENT(int i) {
return (i/2);
}
int LEFT(int i) {
return 2*i;
}
int RIGHT(int i){
return (2*i)+1;
}
void scambia(int HEAP[], int ind1, int ind2){
int appo;
appo = HEAP[ind1];
HEAP[ind1]=HEAP[ind2];
HEAP[ind2]=appo;
}
void MAXHEAPIFY(int HEAP[], int i){
int largest;
int l = LEFT(i);
int r = RIGHT(i);
if ((l <= HEAP[0]) && (HEAP[l] > HEAP[i]))
largest = l;
else
largest = i;
if ((r <= HEAP[0]) && (HEAP[r] > HEAP[largest]))
largest = r;
if (largest != i) {
scambia(HEAP,i,largest);
MAXHEAPIFY(HEAP,largest);
}
}
void BUILD_MAXHEAP(int HEAP){
int i;
HEAP[0] = HEAP[N-1];
for (i=(HEAP[N-1]/2);i>0;i--)
MAXHEAPIFY(HEAP,i);
}
void HEAP_SORT(int HEAP[]) {
int i;
BUILD_MAXHEAP(HEAP);
for(i=HEAP[N-1];i>1;i--) {
scambia(HEAP,1,i);
(HEAP[0])--;
MAXHEAPIFY(HEAP,1);
}
}
Corso di Algoritmi e Strutture Dati
APPUNTI SUL LINGUAGGIO C
Esercizi di base
FINE