Fibonacci Heaps
e il loro
utilizzo
nell’algoritmo di Prim
Paolo Larcheri 52SI
Cosa vedremo
Cos’è uno heap
Cenni sull’analisi ammortizzata
Cosa sono gli Heap di Fibonacci
Gli algoritmi di Minimum Spanning Tree
L’utilizzo degli Heap di Fibonacci
nell’algoritmo di Prim
Complessità dell’algoritmo di Prim
Esempio di funzionamento dell’algoritmo
di Prim
Gli heap
Lo heap, in generale, è una struttura dati
atta a contenere un insieme di dati ordinabili
A prescindere dall’implementazione gli heap
devono fornire le seguenti operazioni:
INSERISCI: inserimento di un nuovo elemento
TROVA-MIN: ricerca dell’ elemento con chiave minima
ESTRAI-MIN: estrazione dell’elemento con chiave minima
UNIONE: “fusione” di due heap
DECREMENTA-CHIAVE: dato un elemento dello heap e un
nuovo e minore valore per la chiave dello stesso, aggiorna
la chiave al nuovo valore
CANCELLA: cancellazione di uno specifico elemento
Gli Heap di Fibonacci (1)
Introdotti da Fredman e Tarjan nel 1987
Possono essere considerati un’ottima
implementazione di Heap!!
Sono stati progettati ispirandosi
all’analisi ammortizzata al fine di
ottenere ben precisi costi.
Cos’è l’analisi ammortizzata
L’analisi ammortizzata mira ad esprimere il tempo di
esecuzione di un’intera sequenza di operazioni
attribuendo un costo nominale ad ogni tipologia di
operazione (inserimento, cancellazione, …).
Anche se una singola operazione può forare il suo
costo nominale, l’importante e che il costo
complessivo dell’intera sequenza resti entro la somma
dei costi nominali per le singole operazioni che la
compongono.
Ovviamente vogliamo dichiarare dei costi nominali il
piu bassi possibili!
Gli Heap di Fibonacci (2)
Le complessità delle operazioni:
Operazione
costo reale
INSERISCI
O(1)
O(1)
O(1)
O(lg(n) + t(H))
O(1)
O(lg(n))
O(1)
O(1)
O(lg(n))
O(1)
O(lg(n) + t(H))
O(lg(n))
TROVA-MIN
ESTRAI-MIN
UNIONE
DECR-CHIAVE
CANCELLA
costo amm.
t(H): numero di radici dello Heap di Fibonacci
Gli Heap di Fibonacci (3)
Gli Heap di Fibonacci sono costituiti da una
lista di alberi caratterizzati ciascuno dall’
“ordinamento parziale dello heap”: la chiave
di ogni nodo è minore o uguale alla chiave
dei figli; in questo modo è garantito che il
nodo con chiave minima è una delle radici
Ogni elemento dello Heap di Fibonacci punta
al nodo-padre
Ogni nodo punta alla lista dei figli
Gli Heap di Fibonacci (4)
Ogni istanza di Heap di Fibonacci è
costituita dai seguenti attributi:
puntatore alla lista delle radici
puntatore al nodo con chiave minima
numero complessivo di alberi contenuti
nello Heap
numero totale di nodi presenti nello Heap
Gli Heap di Fibonacci (5)
Ogni elemento dello Heap di Fibonacci è
collegato direttamente al nodo-padre
Inoltre i suoi figli sono collocati in una lista
Gli attributi di ogni nodo sono:
puntatore al nodo-padre
puntatore alla lista dei figli
2 puntatori: uno al suo fratello destro e uno al suo
fratello sinistro
il grado (intero): numero dei suoi figli
chiave: il valore del nodo
Gli Heap di Fibonacci (6)
Rappresentazione “logica ” di uno Heap di
Fibonacci all’interno di un calcolatore:
Minimum Spanning Tree:
nozioni fondamentali
Dato un grafo G(N, E) connesso, pesato e
non orientato è sempre possibile trovare il
suo MST, cioè quell’albero T(N, E2) (E2 E)
per cui la somma di tutti i pesi degli archi
appartenenti a E2 è minima
Chiaramente se il grafo G è un albero, il suo
MST sarà G stesso
Se G possiede archi con peso uguale è
possibile che esistano più MST per G
Minimum Spanning Tree:
algoritmi
Gli algoritmi più noti sono
Algoritmo di Prim
Algoritmo di Kruskal
Algoritmo di Kruskal
L’algoritmo di Kruskal è di tipo “Greedy”.
Consiste nell’ordinare tutti gli archi del grafo
secondo il loro peso. Inizialmente T è
composto da i soli nodi di G. Vanno aggiunti
(seguendo l’ordine di peso) uno a uno tutti gli
archi che non generano cicli in T.
L’operazione più costosa è ordinare gli archi;
utilizzando un “buon” algoritmo di
ordinamento, l’algoritmo di Kruskal costa
O(mlog n)
Algoritmo di Prim
Grafo G(N, E1) -> grafo
Albero T(N, E2) -> MST NB: E2 E1
Albero Prim(Grafo)
{
considera T formato da un nodo e da nessun arco;
while(esistono nodi in T adiacenti a un nodo non in T)
{
seleziona l’arco di peso minimo che collega un
nodo in T con un nodo non in T;
aggiungi a T sia l’arco selezionato che il nuovo
nodo;
}
return T;
}
Algoritmo di Prim
Nell’algoritmo di Prim è indispensabile
utilizzare una struttura dati che contenga ad
ogni passo della computazione tutti gli archi
candidati all’inserimento in T, ossia gli archi
che connettono un nodo in T con uno non in
T
Bisogna quindi ad ogni iterazione effettuare
degli inserimenti e o delle sostituzioni
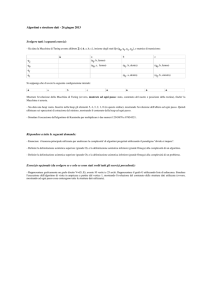
Algoritmo di Prim:
le sostituzioni
Ad ogni iterazione, per ogni nodo v non ancora in T,
basta tenere traccia del miglior arco e(v) che lo
connetta ad un nodo già in T.
Di fatto, per ogni nodo v non in T, terremo traccia
dell’estremo in T di e(v), (NULL se nessun arco
incidente in v ha l’altro estremo in T).
= arco con chiave minima
= archi presenti nella SD
a
p
T
a
min
q
p
q
T
b
q<p
Algoritmo di Prim:
utilizzo degli Heap di Fibonacci
Gli Heap di Fibonacci si prestano
particolarmente “bene” a svolgere
questa funzione mediante l’operazione
DECR-CHIAVE
Come visto prima questa operazione ha
costo (ammortizzato) costante
Algoritmo di Prim:
utilizzo degli Heap di Fibonacci
n-1
Albero Prim(Grafo G) {
considera T formato da un nodo scelto a caso;
FH.inserisci(tutti gli archi del nodo scelto);
while(anew = FH.estraiMin()) {
nnew = nodo dell’arco appena estratto che
non appartiene a T;
T.inserisci(nnew, anew);
for each(x congiunto a nnew da un arco y) {
if(x non appartiene a T)
if(FH contiene arco z che congiunge x a T)
2m
FH.decrChiave(z, y);
else
FH.inserisci(y);
}
}
return T;
}
Algoritmo di Prim:
complessità ammortizzata
WHILE: a ogni iterazione viene effettuata una
ESTRAI-MIN che come abbiamo visto ha
costo ammortizzato pari a O(lg n)
FOR EACH: a ogni iterazione viene eseguita
una DECR-CHIAVE o una INSERISCI aventi
entrambe costo ammortizzato costante
TOTALE: il costo totale ammortizzato è quindi
O(m + n(lg n))
Algoritmo di Prim:
osservazioni finali (1)
Il costo dell’algoritmo di Prim con gli
Heap di Fibonacci dipende anche dal
numero di archi
Quindi:
Per grafi densi la complessità risulta essere
O(n²)
Per grafi sparsi la complessità risulta essere
O(n(lg n))
Algoritmo di Prim:
osservazioni finali (2)
ATTENZIONE: per grafi densi risulta essere
più efficiente l’utilizzo di strutture dati
semplici (es: liste) in quanto la complessità
della struttura degli Heap di Fibonacci
comporta un’espansione della costante
moltiplicativa non rilevabile a causa della
notazione asintotica
Per capirci:
liste
→ O(an²)
Heap di Fibonacci
→ O(bn²)
a«b
Algoritmo di Prim:
esempio (1)
2
18
6
6
1
8
13
4
12
10
17
8
15
1
3
14
7
4
3
20
5
Algoritmo di Prim:
esempio (2)
2
18
6
6
1
8
13
4
12
10
17
8
15
1
3
14
7
4
3
20
5
Algoritmo di Prim:
esempio (3)
2
18
6
6
1
8
13
4
12
10
17
8
15
1
3
14
7
4
3
20
5
Algoritmo di Prim:
esempio (4)
2
18
6
6
1
8
13
4
12
10
17
8
15
1
3
14
7
4
3
20
5
Algoritmo di Prim:
esempio (5)
2
18
6
6
1
8
13
4
12
10
17
8
15
1
3
14
7
4
3
20
5
Algoritmo di Prim:
esempio (6)
2
18
6
6
1
8
13
4
12
10
17
8
15
1
3
14
7
4
3
20
5
Algoritmo di Prim:
esempio (7)
2
18
6
6
1
8
13
4
12
10
17
8
15
1
3
14
7
4
3
20
5
Algoritmo di Prim:
esempio (8)
2
18
6
6
1
8
13
4
12
10
17
8
15
1
3
14
7
4
3
20
5
Algoritmo di Prim:
esempio (8)
2
18
6
6
1
8
13
4
12
10
17
8
15
1
3
14
7
4
3
20
5