Lezioni di Astronomia

Lezioni di Astronomia
3- Le stelle
Liceo Scientifico Copernico
Bologna 8 aprile 2010
1
Le stelle visibili ad occhio nudo sono circa 6000
(3000 per emisfero)
Le stelle nella nostra galassia sono 200-400
miliardi
Le galassie sono 100-200 miliardi
Le stelle sono
200 109  200 109  40000 1018
410
22
2
Le stelle
hanno luminosità
e colore diverso
Sirio
3
Betelgeuse
4
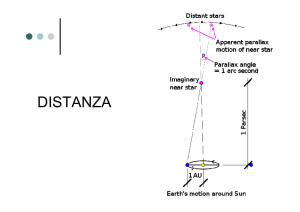
L’intensità luminosa dipende dalla
distanza
L
f 
4d 2
5
Se conosciamo la luminosità possiamo
determinare la distanza
L
f 
2
4d
Se conosciamo la distanza possiamo
determinare la luminosità
6
Esempio pratico: misuriamo l’intensità della
radiazione solare e determiniamo la luminosità del
sole
f  1.4 10 W / m
3
2
d  1U . A.  1.5 108 km
L  f  4d 2
L  1.4 10  4 (1.5 10 )
3
11
2
L  4 1026 watt
7
Gli astronomi misurano le intensità luminose
utilizzando una scala logaritmica (magnitudini)
m  2.5Log ( f )  Cost
Dalla definizione di magnitudine discende che
m1  m2  2.5Log ( f )1  2.5Log ( f 2 )
 f1 
m1  m2  2.5Log  
 f2 
8
m è detta magnitudine apparente
(poichè dipende dalla distanza)
Si definisce magnitudine assoluta, M, la
magnitudine apparente corrispondente ad una
distanza di 10 pc
 f1 
m1  m2  2.5Log  
 f2 
 f 

m  M  2.5Log 

f
 10 pc 
9
Poichè :
L
f 
4d 2
L
f10 
2
4 10
 L 


2
m  M  2.5 Log  4d 
 L 

2 
 4 10 
2
10


m  M  2.5Log  2 
 d 
m  M  5  5Log (d )
10
Sirio appare più luminosa di Betelguese
ma lo è davvero ?
Sirio : m=-1.46, d=8.6 a.l.
Betelgeuse : m=0.50 , d=640 a.l.
1 a.l.  0.3066 pc
M  m  5  5Log (d )
Sirio : M = 1.43
Betelgeuse : M = -5.96
11
 L1 
M 1  M 2  2.5Log  
 L2 
 L1 
1.43  5.96  2.5Log  
 L2 
 L2 
7.39  2.5Log  
 L1 
 L2  7.39
Log   
 L1  2.5
7.39
L2
2.956
2.5
 10  10  904
L1
12
13
14
15
16
17
1901
18
19
20
21
22
23
F
A
B
O
G
K
24
25
26
M*  0.4  1.2 M O
4 p - 1 He  0.0477 10 kg
-27
E  mc
2
E  0.0477 10 (3 10 )  4.3 10 Joules
27
8
2
-12
27
Peso atomico dell’ H 1.0079
In 1 gr c’e’ una mole di H
M O  2 10 30 kg
23
610
M H  2 10 kg
29
N H  2 10 29 1000  6 10 23
E  2 10 1000  6 10  4.3 10
29
23
12
E  10 joule
43
E 10 43
 26  1017 s  1010 anni
L 10
28
M*  1.2 M O
12C
+ 1H → 13N + γ
13N
→ 13C + e+ + v
13C
+ 1H → 14N + γ
14N
+ 1H → 15O + γ
15O
→ 15N + e+ + v
15N
+ 1H → 12C + 4He
29
Massa stella in unità di
massa solari (x volte la
massa del Sole)
Vita media sulla
sequenza principale
(anni)
60
400.000
10
30.000.000
3
600.000.000
1
10.000.000.000
0.3
200.000.000.000
0.1
3.000.000.000.000
30
4He
8Be
+ 4He ↔ 8Be
+
4He
↔
12C
+γ
M*  0.4 M O
31
32
M*  8 M O
M c  1.4 M O
R  6000  9000 km
  106 g / cm3
33
Sirio A,
M  1.4 M O
L  24LO
Sirio B
M  1.1 M O
L  0.002LO
R  0.0073 R O
34
Nane bianche in M4 (HST 1995)
d=7000 a.l., D=70 a.l., t=12 mld anni
35
IC 418 , Spirograph , d= 2000 a.l., D= 0.2 a.l (HST
sept 1999).
36
NGC 6543 Cat’s eye , d=3000 a.l. t=1000 anni
(HST sept. 1994)
37
NGC 2818, d=10 000 a.l., D= 4 a.l.
(HST, Jan. 2009)
38
M*  8  20 M O
M c  1.4 M O
Rc  10 km
  2 108 10 6 g / cm3
  Fe  He  4n
p  e  n 
56
4
39
1987 A
168 000 anni fa
40
1987A, HST (1999)
41
1994 d, in NGC 4526, d=55 ml. a.l.
42
2008ha , in UGC 12682, d=69 ml. a.l.
43
1054 d.C.
M 1 – Nebulosa del Granchio
44
M*  20 MO
Mc  3 MO
45
2GM
RS  2
c
K U  0
1
2
K  mv
2
1
mM
2
m v G
0
2
R
mM
U  G
R
2GM
v 
R
2
46
2GM
v 
R
2
M  5.9742 10 24 kg
R  6370 km
G  6.67 10 11 m3kg 1s 2
11
24
2

6
.
67

10

5
.
97

10
v2 
3
3
6.37 10 10
7
2

6
.
67

5
.
97

10
2
7
v 
 12.5 10
6.37
v  11181 m/s
v  11.18 km/s
47
2GM
v 
R
2
2GM
RS  2
c
2GM
R 2
v
M O  2 10 30 kg
c  3 105 km / s
2  6.67 10 11  2 10 30 4  6.67 1019
RS 

5
3 2
16
(3 10 10 )
9 10
RS  2.96 10 3 m
48
49
d= 2700 a.l
D = 10 a.l
t = 3 mld anni
N = 500
50
d= 33900 a.l
D = 90 a.l
N= 500 000
t= 8 mld anni
51
M 46,
d=5400 a.l, D=30 a.l,
N= 500,t=300 ml. anni
N 2438, d= 3000 a.l
t=3-4 miliardi anni
M 47,
d=1600 a.l, D=10 a.l,
N= 50, t=80 ml. anni
52