SVILUPPO DI UN METODO DI
CALIBRAZIONE DI UN SISTEMA
STEREOSCOPICO PER LA MISURA
DELLA LARGHEZZA DI PRODOTTI
PIANI LAMINATI A CALDO
Laureando: MASSIMO DAL FORNO
Relatore: Chiar.mo Prof. Ing. THOMAS PARISINI
Correlatore: Ing. ALESSANDRO ARDESI
CDL: Ing. Elettronica
Oggetto della tesi: calibrazione di un sistema
stereoscopico per la misura di laminati piani.
Realizzazione: algoritmo software su
piattaforma Matlab.
Lavoro svolto presso Danieli Automation (UD)
LAMINATO OTTENUTO DAL PROCESSO DI
LAVORAZIONE:
l
SI VUOLE CONOSCERE LA
DIMENSIONE “LARGHEZZA”
Specifiche:
• Campo di misura: 400~1800 mm
• Tolleranza: ±2mm
Vantaggi della stereoscopia:
• Misura indipendente dallo spessore
dell’oggetto;
• Possibilità di utilizzare telecamere CCD di
dimensione ridotta;
• Notevole distanza dei CCD dal materiale da
misurare incandescente.
SISTEMA DI MISURA PROPOSTO
SENSORE CCD SX
SENSORE CCD DX
Y
OBIETTIVO
DX
LASER
DX
OBIETTIVO
SX
LASER
SX
X
OGGETTO
DA
MISURARE
Problemi introdotti dal sistema:
• Non linearità delle ottiche;
• Rumore;
• Quantizzazione dei CCD;
Scopo del progetto: Calibrare il sistema
affinché lavori correttamente su un’ampia
gamma di valori di larghezza.
Calibrazione
La procedura di calibrazione può essere
scomposta nelle seguenti fasi:
1. Proiezione della luce sull’oggetto di larghezza
nota;
2. Acquisizione dei dati rilevati dai CCD;
3. Iterazione dei due punti precedenti con altri
materiali di larghezza diversa;
4. Calibrazione del sistema, eseguita mediante
la correzione SW dei valori dei parametri fisici
del sistema.
Misura generica
La misura avviene secondo le seguenti fasi:
1. Proiezione della luce sul materiale di larghezza
incognita;
2. Acquisizione dei dati rilevati dai CCD;
3. Calcolo della larghezza mediante la funzione di
trasferimento del sistema ottico.
Modello del sistema ottico
SENSORE CCD DX
CCDcentre
SENSORE CCD SX
CCDcentre
ED1
Asse
Y
ES2
βD
ED2
ES1
βS
IS
ID
αD
OD
Spigolo 1
P1(X1,Y1)
αS
OS
Spigolo 2
P2(X2,Y2)
Asse X
Oggetto da
misurare
Segnali video acquisiti dai CCD
EdgeD1
EdgeD2
EdgeS1
EdgeS2
I dati acquisiti dal sistema sono i seguenti:
•
•
•
•
EdgeD1
EdgeD2
EdgeS1
EdgeS2
Mentre i parametri sono:
•
•
•
•
•
•
•
•
•
Os
Is
αs
βs
Od
Id
αd
βd
CCDcentre
Funzione di trasferimento del sistema
Permette il calcolo delle coordinate cartesiane dei
punti
-P1(X1,Y1);
-P2(X2,Y2);
e della larghezza dell’oggetto:
larghezza
X 1 X 2 Y 1 Y 2
2
2
Espressione generale della larghezza in funzione delle
variabili di sistema:
larghezza f ( Ed1, Ed 2, Es1, Es2, CCDc, Od , Id , d , d , Os , Is, s; s)
Fronti
rilevati
Funzione
“larghezza”
Parametri
In cui
- Ed1,Ed2,Es1,Es2 sono i fronti rilevati,
- CCDc è il centro del CCD
Larghezza
dell’oggetto
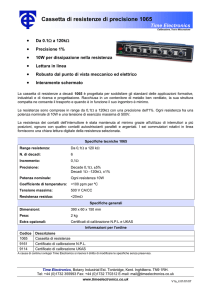
Funzione costo relativa ad una singola acquisizione:
costo (stima _ larghezza valore _ reale ) 2
Fronti
rilevati
Funzione
“costo”
Parametri
[1]
Costo della
misura
Funzione costo relativa ad una singola acquisizione:
costo g ( Ed1, Ed 2, Es1, Es2, CCDc, Od , Id , d , d , Os , Is, s; s)
Procedura di calibrazione:
• Minimizzare la funzione costo, calcolando i
valori dei parametri Od, Id, αd, βd, Os, Is, αs,
βs corrispondenti.
Metodi di ricerca del minimo di un campo
scalare:
• Studio di funzione
molto complesso per
una funzione di otto
variabili
• Algoritmo numerico
proprietà del gradiente di
un campo scalare
• Il gradiente calcolato in un punto rappresenta la
direzione di massimo incremento;
• Il suo opposto rappresenta la direzione di massimo
decremento.
Funzione costo data dalla media degli errori dovuti a
più rilevazioni di campioni diversi:
1
cos toMEDIO
N
N
2
stima
_larghezza
(
i
)
valore
_
reale
(
i
)
i 1
Scopo della funzione “costo medio”:
• Ottenere un set di parametri universali.
E’ necessario scegliere opportunamente le dimensioni
dei campioni da utilizzare nella calibrazione
complessiva del sistema.
[2]
LA PROCEDURA DI CALIBRAZIONE
•
•
•
Si eseguono un certo numero Nril di rilevazioni da
campioni di larghezza nota.
Scelta di N misure (con N < Nril) con le quali calibrare
il sistema.
Minimizzazione della funzione costo complessiva,
ottenuta dalla media dei singoli costi di queste N
rilevazioni.
Si otterranno così i valori degli otto parametri
Od, Id, αd, βd, Is, Os, αs, βs, corretti secondo
l’algoritmo di calibrazione globale.
Algoritmi sviluppati:
• Algoritmo di selezione delle misure da
calibrare;
• Algoritmo di calibrazione per una singola
acquisizione;
• Algoritmo di calibrazione complessivo.
ALGORITMO DI SELEZIONE DELLE
MISURE DA CALIBRARE
Discrimina quali delle Nril rilevazioni potranno essere
utilizzate in calibrazione.
Esse verranno scelte in base alle seguenti caratteristiche:
• Dovranno contribuire in modo non ridondante alla
calibrazione complessiva del sistema;
• Dovranno consentire la stima di un set di parametri
universale.
ALGORITMO DI CALIBRAZIONE PER
UNA SINGOLA ACQUISIZIONE
Calcola i parametri ottimi per una singola acquisizione
minimizzando la relativa funzione costo.
Il procedimento è strutturato secondo le seguenti fasi:
• Si parte dal punto rappresentato dai parametri misurati.
• Viene calcolata la direzione di massimo decremento.
• Al fine di minimizzare la funzione costo, è sufficiente
spostarsi all’interno del dominio di essa secondo la
direzione di decremento.
• Si procede iterando le precedenti operazioni fino a
quando l’errore scende al di sotto di una soglia
prefissata.
I parametri ottimi per una singola rilevazione sono stati ora
calcolati.
ALGORITMO DI CALIBRAZIONE
COMPLESSIVO
Minimizza la funzione costo media data dalle rilevazioni
selezionate in precedenza.
La procedura di ricerca del minimo è simile a quella del
precedente algoritmo, l’unica differenza sta nel fatto
che la funzione costo da ottimizzare è quella globale, e
permette la stima di un set di parametri adatti alla
misura in un ampio range di valori di larghezze.
MISURE E RISULTATI SPERIMENTALI
Campioni utilizzati:
1. 415mm
2. 500mm
3. 615mm
4. 900mm
5. 1200mm
Per ciascun campione sono state effettuate
13 misure con il centro posto nelle seguenti
posizioni:
• Centro del campione posto in X=0, Y=0;
• Centro traslato di ±10, ±20, ±30 mm rispetto
all’asse X;
• Centro traslato di ±10, ±20, ±30 mm rispetto
all’asse Y;
Esempio: calibrazione eseguita con il primo campione
posto in posizione centrale
ERRORE IN FUNZIONE DI UNO SPOSTAMENTO LUNGO X [mm]
ERRORE
LIMITI MAX E MIN
SPOSTAMENTO LUNGO X [mm]
Errori dovuti alla stima compresi nel margine di ±2mm
ERRORE IN FUNZIONE DI UNO SPOSTAMENTO LUNGO Y [mm]
ERRORE
LIMITI MAX E MIN
SPOSTAMENTO LUNGO Y [mm]
La stima della larghezza non è corretta traslando l’oggetto
rispetto ad Y.
Calibrazione eseguita con i campioni da 415 e
615mm posti al centro del sistema di riferimento.
ERRORE DOVUTO ALLA STIMA DEI CAMPIONI [mm]
ERRORE
LIMITI MAX E MIN
N° CAMPIONE
Calibrazione eseguita con i campioni da 415 e 900mm
ERRORE DOVUTO ALLA STIMA DEI CAMPIONI [mm]
ERRORE
LIMITI MAX E MIN
N° CAMPIONE
Restrizione del campo di misura da 415 a 615mm.
Misure traslate lungo Y eliminate.
Risultati degli algoritmi descritti.
ERRORE DOVUTO ALLA STIMA DEI CAMPIONI [mm]
ERRORE
LIMITI MAX E MIN
N° RILEVAZIONE
Conclusioni
Gli algoritmi descritti funzionano
correttamente in un campo di misura di
200mm, sono ammesse traslazioni lungo X;
mentre la misura non è corretta se il
campione viene traslato lungo Y.
Le possibili cause di questi malfunzionamenti
sono:
• Le non linerità del sistema ottico;
• La quantizzazione del CCD;
Sviluppi futuri
• Analisi dettagliata della funzione ottica degli
obiettivi fotografici;
• Identificazione del modello;
• Utilizzo di parametri variabili in funzione della
classe dimensionale dell’oggetto.