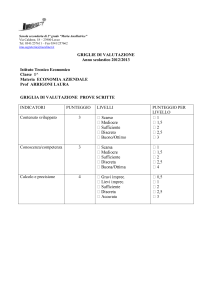
Corso di Statistica – Docente: Domenico Vistocco ESERCIZIO 1
Il test di ammissione alla prestigiosa Università STUDY produce punteggi che seguono una distribuzione
normale con media 500 e scarto quadratico medio 100. Il punteggio necessario per superare il test è stabilito
pari a 534
a) Calcolare la probabilità di ottenere un punteggio superiore al punteggio medio:
b) Calcolare la probabilità di ottenere un punteggio uguale al punteggio medio:
c) Calcolare la frazione di studenti che riescono a superare il test di ammissione:
d) Calcolare la frazione di studenti che non riescono a superare il test di ammissione:
e) Calcolare la frazione di studenti che ottengono un punteggio esattamente uguale al punteggio minimo
richiesto per superare il test di ammissione:
f) Calcolare la frazione di studenti che ottengono un punteggio minore di 421:
g) Calcolare la frazione di studenti che ottengono un punteggio tra 400 e 600:
h) Calcolare la frazione di studenti che ottengono un punteggio tra 300 e 700:
i) Calcolare la frazione di studenti che ottengono un punteggio tra 200 e 800:
Compito n. 12 – a.a. 2014/15 1 Corso di Statistica – Docente: Domenico Vistocco l) Calcolare la frazione di studenti che ottengono un punteggio superiore a 800:
m) Calcolare la frazione di studenti che ottengono un punteggio superiore a 1000:
n) Calcolare la frazione di studenti che ottengono un punteggio inferiore a 1000:
ESERCIZIO 2
Il test di ammissione alla prestigiosa Università STUDY produce punteggi che seguono una distribuzione
normale con media 500 e scarto quadratico medio 100. Il punteggio necessario per superare il test è stabilito
pari a 534. Calcolare:
1° quartile
2° quartile
3° quartile
1° percentile
99° percentile
5° percentile
95° percentile
10° percentile
Compito n. 12 – a.a. 2014/15 2 Corso di Statistica – Docente: Domenico Vistocco 90° percentile
25° percentile
75° percentile
50° percentile
ESERCIZIO 3
Si supponga che il numero di km percorsi da un'autovettura prima che la sua batteria sia esausta si
distribuisca come una variabile aleatoria esponenziale di media 10000 km.
a) Se una persona intraprende un viaggio di 5000 km qual è la probabilità che lo porti a termine senza
sostituire la batteria?
b) Qual è la probabilità che la batteria appena acquistata duri più di 10000 km?
c) Qual è la probabilità che la batteria appena acquistata duri esattamente 10000 km?
ESERCIZIO 4
Sia X una v.c. uniforme continua sull'intervallo [0, 10]. Scrivere la funzione di densità e tracciarne il grafico:
Compito n. 12 – a.a. 2014/15 3 Corso di Statistica – Docente: Domenico Vistocco Scrivere la funzione di ripartizione e tracciarne il grafico:
ESERCIZIO 5
Lo studente Pietro Pane arriva alla fermata dell'autobus per l'Università alle ore 8:00 e sa che passerà un
autobus in un momento distribuito uniformemente tra le 8:00 e le 8:20.
a) Qual è la probabilità che debba aspettare più di 10 minuti?
b) Qual è la probabilità che debba aspettare non più di 10 minuti?
c) Qual è la probabilità che debba aspettare esattamente 10 minuti?
d) Qual è la probabilità che debba aspettare tra 5 è 10 minuti?
e) Qual è la probabilità che debba aspettare più di 15 minuti?
f) Se alle 8:10 l'autobus non è ancora arrivato, qual è la probabilità che tu debba aspettare almeno altri 5
minuti?
Compito n. 12 – a.a. 2014/15 4