CRITERI DI ISOMETRIA (o di CONGRUENZA)
dei TRIANGOLI
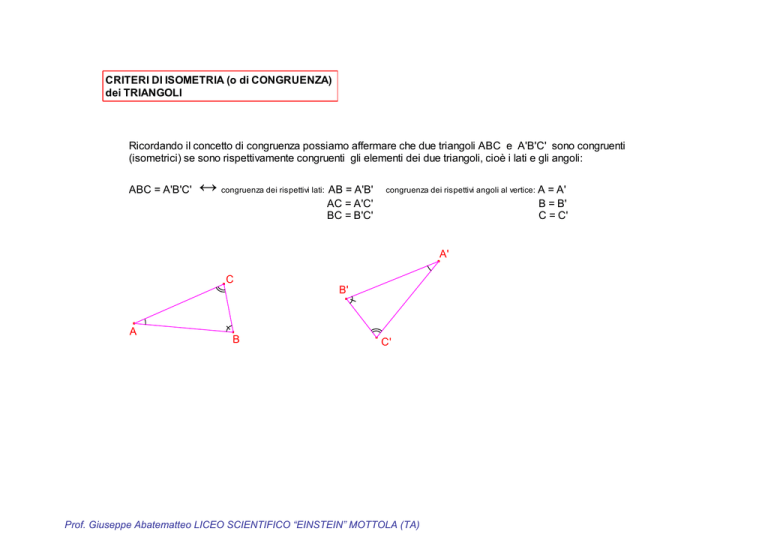
Ricordando il concetto di congruenza possiamo affermare che due triangoli ABC e A'B'C' sono congruenti
(isometrici) se sono rispettivamente congruenti gli elementi dei due triangoli, cioè i lati e gli angoli:
ABC = A'B'C'
↔ congruenza dei rispettivi lati: AB = A'B'
congruenza dei rispettivi angoli al vertice:
AC = A'C'
BC = B'C'
A'
C
A
B
B'
C'
Prof. Giuseppe Abatematteo LICEO SCIENTIFICO “EINSTEIN” MOTTOLA (TA)
A = A'
B = B'
C = C'
1° C riterio: due triangoli sono isometrici se hanno due lati e l'angolo compreso
rispettivamente isomentrici.
Ipotesi
Tesi
se congruenza di due lati rispettivamente: AB = A'B'
→
AC = A'C'
allora
C
ABC = A'B'C
congruenza di un angolo rispettivamente: A = A'
α
A
B
2° C riterio: due triangoli sono isometrici se hanno due angoli e il lato compreso
rispettivamente isomentrici.
s e congruenza di due angoli, rispettivamente: A = A'
B = B'
A'B'
congruenza di un lato, rispettivamente:
→
a llora
ABC = A'B'C
α
AB =
β
A
B
Prof. Giuseppe Abatematteo LICEO SCIENTIFICO “EINSTEIN” MOTTOLA (TA)
3° Criterio: due triangoli sono isometrici se hanno i tre lati
rispettivamente isomentrici.
C
osservazione: non si può dire lo stesso in riferimento ai tre angoli.
se
congruenza di tre lati, rispettivamente:
A B = A 'B '
A C = A 'C '
→
a llo ra
B C = B 'C '
A B C = A 'B 'C
A
B
C'
C
es. relativo all'osservazione: come si nota i due
triangoli hanno i rispettivi angoli congruenti ma essi
non lo sono
B
A
A'
B'
Prof. Giuseppe Abatematteo LICEO SCIENTIFICO “EINSTEIN” MOTTOLA (TA)
OSSERVAZIONI sui triangoli
Osservaz. generale: se due triangoli sono isometrici allora ogni elemento del 1° triangolo è congruente al
corrispondente elemento del 2° triangolo.
T
In un triangolo isoscele gli angoli alla base sono congruenti.
T
Un triangolo con due angoli congruenti è isoscele e ha per base il lato adiacente ai due angoli.
T
In un triangolo isoscele l'atezza relativa alla base,
la mediana relativa alla base e
la bisettrice relativa all'angolo al vertice coincidono. (dimostrare col cabri)
esercizio: dimostrare quali elementi coincidono in un triangolo rettangolo.
esercizio: dimostrare quando in un poligono (in particolare per quali triangoli)
esiste una coincidenza fra ortocentro,
baricentro,
incentro,
circocentro.
Prof. Giuseppe Abatematteo LICEO SCIENTIFICO “EINSTEIN” MOTTOLA (TA)
TEOREMI DELL'ANGOLO ESTERNO DI UN TRIANGOLO
1°Teor.
Considerato un triangolo qualsiasi, ogni angolo esterno é maggiore di qualsiasi angolo interno
ad esso non adiacente.(dimostrare)
Di conseguenza:
La somma di due angoli interni è minore di 180°.
Quindi:
non può avere due angoli retti;
non può avere due angoli ottusi;
non piò avere un angolo retto e uno ottuso;
Cioè: in un triangolo si hanno sempre due angoli acuti.
2°Teor.
Considerato un triangolo qualsiasi, ogni angolo esterno é congruente alla somma dei due
C
angoli interni ad esso non adiacenti.
45,7 °
A
26,9 °
B
72,6 °
T
Considerato un triangolo qualsiasi, se esso ha due lati diversi, saranno diversi anche i
corrispondenti angoli al vertice (e viceversa); e precisamente
al lato maggiore corrisponde l'angolo maggiore e
al lato minore corrisponde l'angolo minore.
(Osservare tale proprietà in un triangolo isoscele, equilatero e in un triangolo qualsiasi)
T
Considerato un triangolo qualsiasi,
ogni lato è minore della somma degli altri due;
ogni lato è maggiore della differenza degli altri due.
Prof. Giuseppe Abatematteo LICEO SCIENTIFICO “EINSTEIN” MOTTOLA (TA)
T
ESISTENZA E UNICITA'
della bisettrice: esiste una ed una sola retta che divide un
angolo in due parti congruenti.
del punto medio di un segmento: esiste un punto ed uno
solo che divide un segmento in due parti congruenti.
25,5 °
25,5 °
M
3,00 cm
3,00 cm
6,00 cm
P
della perpendicolare ad una retta per un punto: esiste
una ed una sola retta passante per un punto e
perpendicolare ad una retta data.
Prof. Giuseppe Abatematteo LICEO SCIENTIFICO “EINSTEIN” MOTTOLA (TA)
P
Notazione particolare riguardante un poligono qualsiasi:
T
Considerato un qualsiasi poligono convesso di n lati, la somma degli angoli interni è congruente a tanti angoli
piatti quanti sono i lati del poligono meno due;
cioè 180°(n - 2).
D
A
Sia P un punto interno qualsiasi.
(Dimostrare il teorema tenendo conto delle proprietà dei triangoli)
P
C
B
Considerato un poligonpo regolare di n lati, l'ampiezza di ogni angolo interno è dato da
Prof. Giuseppe Abatematteo LICEO SCIENTIFICO “EINSTEIN” MOTTOLA (TA)
180°(n - 2)/n












