STABILITÀ DELL’EQILIBRIO
5
Tensione critica e snellezza
Al carico critico euleriano
Ncr =
π 2 EI
(1)
l 20
dove ℓ0 è la lunghezza libera di inflessione corrispondente alla semilunghezza d’onda
della sinusoide formata dalla linea elastica, corrisponde la tensione critica
σcr =
N cr π 2 E
= 2
A
λ
(2)
dove
λ=
l0
ρ min
(3)
è la snellezza dell’asta e ρmin il raggio d’inerzia minimo della sezione trasversale
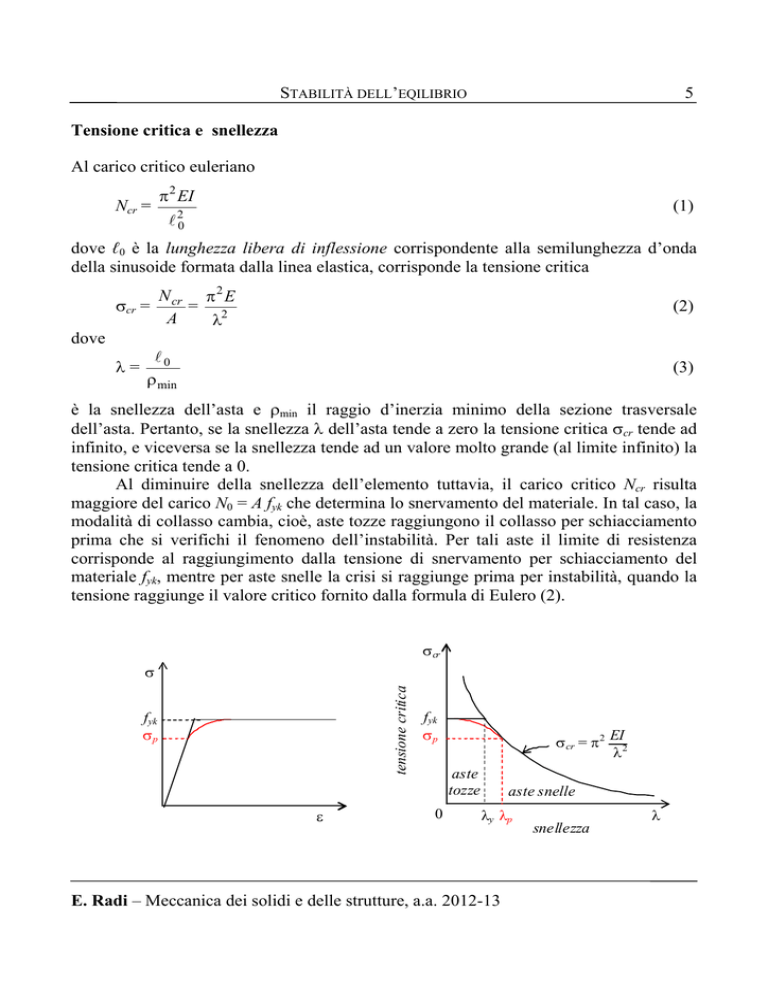
dell’asta. Pertanto, se la snellezza λ dell’asta tende a zero la tensione critica σcr tende ad
infinito, e viceversa se la snellezza tende ad un valore molto grande (al limite infinito) la
tensione critica tende a 0.
Al diminuire della snellezza dell’elemento tuttavia, il carico critico Ncr risulta
maggiore del carico N0 = A fyk che determina lo snervamento del materiale. In tal caso, la
modalità di collasso cambia, cioè, aste tozze raggiungono il collasso per schiacciamento
prima che si verifichi il fenomeno dell’instabilità. Per tali aste il limite di resistenza
corrisponde al raggiungimento dalla tensione di snervamento per schiacciamento del
materiale fyk, mentre per aste snelle la crisi si raggiunge prima per instabilità, quando la
tensione raggiunge il valore critico fornito dalla formula di Eulero (2).
σ cr
tensione critica
σ
fyk
σp
ε
fyk
σp
σ cr = π2
aste
tozze
0
EI
λ2
aste snelle
λy λp
E. Radi – Meccanica dei solidi e delle strutture, a.a. 2012-13
snellezza
λ
STABILITÀ DELL’EQILIBRIO
6
Nel diagramma σcr - λ si individuano due zone distinte separate dal valore λy
della snellezza. Le aste di snellezza λ < λy vengono definite tozze; per esse la tensione
critica euleriana è superiore a quella di schiacciamento (σcr > fyk). La seconda categoria è
rappresentata dalle aste snelle con λ > λy per le quali si ha σcr < fyk.
La tensione massima che l’asta può sopportare corrisponde a fyk nel campo delle
aste tozze (tratto costante) e alla σcr definita in (2) nel campo delle aste snelle (tratto
iperbolico). Questi due campi sono delimitati dal valore di snellezza λy per il quale la
tensione critica euleriana σcr eguaglia la tensione di snervamento fyk, cioè
π2 E
= fyk
λ2y
⇒
λy = π
E
f yk
(4)
La snellezza λy è definita snellezza critica e dipende solo dal materiale. In
particolare, λy si riduce all’aumentare della resistenza fyk del materiale.
Considerando i valori delle tensioni di snervamento fyk per gli acciai laminati, i
valori della snellezza critica λy (riportati in tabella) variano circa tra 75 e 100
spessore < 40 mm
spessore > 40 mm
acciaio
fyk
λy
fyk
λy
S235
235
93.91
210
99.34
S275
275
86.81
250
91.05
S355
355
76.41
315
81.11
In realtà la validità della formula di Eulero è limitata dalla richiesta che la σcr non
superi il valore della tensione normale al limite di proporzionalità indicato con σp.
Per la verifica di stabilità delle aste compresse si utilizzano diagrammi simili a
quello della figura precedente, nei quali i valori della tensione e della snellezza sono resi
adimensionali. In particolare, in ordinate si riporta l’andamento del rapporto
χ=
σ cr
N cr
1
=
= 2
λ
f yk
A f yk
(5)
definito coefficiente di riduzione, in funzione della snellezza adimensionale
λ=
λ
=
λy
A f yk
N cr
E. Radi – Meccanica dei solidi e delle strutture, a.a. 2012-13
(6)
STABILITÀ DELL’EQILIBRIO
7
coeff. di riduzione
χ
1
χ=
aste
tozze
0
1
λ2
aste snelle
1
snellezza adimensionale
λ
Effetti delle imperfezioni nelle aste reali
L’asta di Eulero soggetta ad una forza perfettamente centrata rappresenta un limite
ideale a cui le situazioni reali possono tendere, ma mai raggiungere completamente.
La presenza di imperfezioni nelle aste reali determina una riduzione del carico
critico Ncr rispetto a quello fornito dalla formula di Eulero (1). Le imperfezioni possono
essere geometriche (non perfetta linearità della linea d’asse dell’asta, non perfetta
verticalità dei pilastri) oppure del legame costitutivo del materiale (legame non
indefinitamente elastico ma elastoplastico) oppure meccaniche (presenza di stati di
tensione interni dovute ai procedimenti di lavorazione dell’acciaio).
In pratica la presenza di queste imperfezioni fa sì che in ogni sezione sia presente
una eccentricità non intenzionale, per cui assieme alla forza assiale è presente anche un
momento flettente iniziale, al quale si aggiunge quello prodotto dagli effetti della
deformazione. La presenza di questo momento cambia sensibilmente il comportamento
dell’asta e di esso si deve tener conto quando si verifica un’asta snella soggetta a carico
assiale. In presenza di imperfezioni, il fenomeno dell’instabilità si manifesta infatti
attraverso un comportamento di tipo asintotico, e non biforcativo come nel caso della
asta di Eulero, con spostamenti sempre più grandi all’aumentare del carico di
compressione, che diventano illimitati in corrispondenza del valore critico del carico.
Pertanto, sebbene il valore del carico critico non sia influenzato dalle imperfezioni, la
struttura può collassare per carichi inferiori al carico critico, in seguito all’entità
eccessiva degli spostamenti.
Per studiare qualitativamente il fenomeno, si analizza ora il problema di un carico
di compressione applicato ad un asta con eccentricità e costante.
E. Radi – Meccanica dei solidi e delle strutture, a.a. 2012-13
STABILITÀ DELL’EQILIBRIO
v
N
l
N
e
N
Ncr
l
x
8
(13)
N v e
v
0
v
Per il problema considerato in figura, le condizioni al contorno da imporre sulla
soluzione generale dell’equazione della linea elastica
v(x) = C1 sin αx + C2 cos αx + C3 x + C4
sono:
v(0) = 0
v′(0) = 0
in x = 0
− EI v′′(ℓ) = − Ne
V=0
in x = ℓ
da cui si ricavano le costanti di integrazione:
C1 = 0
C3 = 0
C4 = − C2 =
e
cos αl
La corrispondente equazione della linea elastica risulta
v( x) =
e
(1 − cos αx)
cos αl
(7)
per cui lo spostamento all’estremità x = ℓ (freccia) diventa
⎛ 1
⎞
v = v(ℓ) = ⎜
− 1⎟ e
⎝ cos αl ⎠
(8)
Sotto un carico di compressione N uguale al carico critico della trave a mensola
π 2 EI
Ncr =
4l 2
(9)
cioè per αℓ = π/2, si ha cos αℓ = 0 e quindi lo spostamento v risulta illimitato. Tuttavia si
possono avere notevoli incrementi di spostamento rispetto alla teoria del I ordine anche
per carichi inferiori al carico critico dell’asta. Tali incrementi di spostamento inducono
E. Radi – Meccanica dei solidi e delle strutture, a.a. 2012-13
STABILITÀ DELL’EQILIBRIO
9
corrispondenti incrementi delle sollecitazioni. In particolare, il momento massimo
all’incastro nella teoria del II ordine risulta pari a
Mmax = N (e + v) =
Ne
cos αl
(10)
Si ha quindi un incremento rispetto al momento Pe calcolato secondo la teoria del
I ordine, che diventa illimitato per P = Pcr. In via approssimata, si può assumere
2
4 Nl 2
N
⎛2 ⎞
=1−
cos αℓ ≈ 1 − ⎜ αl ⎟ = 1 − 2
N cr
π EI
⎝π ⎠
(11)
tale approssimazione è più che accettabile per αℓ < π, come si può osservare in figura
1.0
0.8
0.6
0.4
1− (2x/π)2
cos x
0.2
−π/2
0
π/2
x
Con la stessa approssimazione, dalle (10) e (8) si ha
Mmax =
Ne
Ne
≈
cos αl 1 − N / N cr
⎛
⎞
v0
1
Ne
1
Ne l 2
1
⎜
⎟
≈
=
v≈ ⎜
− 1⎟ e =
1 − N / N cr N cr
1 − N / N cr 2.5EI 1 − N / N cr
⎝ 1 − N / N cr
⎠
(12)
(13)
dove
v0 =
Ne l 2
2 EI
(14)
è la freccia calcolata secondo la teoria del I ordine, cioè valutando le condizioni di
equilibrio nella configurazione indeformata nell’ipotesi di spostamenti infinitesimi.
E. Radi – Meccanica dei solidi e delle strutture, a.a. 2012-13
STABILITÀ DELL’EQILIBRIO
10
Il termine
β=
1
1 − N / N cr
(15)
prende il nome di fattore di amplificazione (β ≥ 1)
A causa dell’incremento che v ed Mmax subiscono al crescere del carico N, la crisi
sopravviene sotto un carico N inferiore al carico critico Ncr.
Effetti della plasticizzazione
Se si considerano inoltre gli effetti della plasticizzazione, il comportamento dell’asta
diventa quello in tratteggio nella figura seguente, a cui corrisponde un carico massimo
Nmax < Ncr. In tal caso infatti, al crescere del carico N la sezione inizia a plasticizzarsi ed
il comportamento della trave si modifica rispetto al comportamento asintotico (13)
corrispondente ad un comportamento infinitamente elastico del materiale.
N
I
II-E
II-EP
Ncr
carico
(13)
(16)
Nmax
0
freccia
a
A fyk a
v
N
N
e
v
Con riferimento ad una sezione IPE o HE di materiale elastico perfettamente
plastico, si può ricavare il carico ultimo di plasticizzazione tenendo conto anche degli
effetti del II ordine. In tal caso, la condizione di equilibrio alla rotazione attorno al
baricentro dell’ala in trazione, valutato nella configurazione deformata, richiede:
N (v + e + a) = 2 a A fyk = a N0
E. Radi – Meccanica dei solidi e delle strutture, a.a. 2012-13
STABILITÀ DELL’EQILIBRIO
11
dove A è l’area dell’ala e N0 = 2A fyk è lo sforzo normale di completa plasticizzazione
(Atot ≈ 2A).
Pertanto, il carico limite della struttura risulta
N=
N0
v+e
1+
a
(16)
Al crescere di v quindi il carico limite N si riduce e tende a zero per v → ∞.
Verifica delle aste compresse secondo NTC 2008 e EC3
Come ricavato in precedenza, la sezione più sollecitata dell’asta pressoinflessa
con eccentricità accidentale e è soggetta ad una forza assiale N e ad un momento
flettente M = β N e. La tensione massima nella sezione è quindi
σmax =
Ne
N
+
A W (1 − N / N cr )
(17)
in cui N e è il momento del primo ordine e W = I/ymax indica il modulo di resistenza della
sezione. Indicando con ρ2 = I/A il raggio di inerzia della sezione elevato al quadrato, la
(12) si può scrivere:
σmax =
N
A
⎞
⎛
m
⎟⎟
⎜⎜1 +
1
N
/
N
−
cr ⎠
⎝
(18)
dove è stato introdotto il rapporto
m=
e A e ymax e
=
=
W
e1
ρ2
(19)
che misura il rapporto tra l’eccentricità accidentale considerata e ed il raggio di nocciolo
e1 = ρ2/ymax, dove ρ2 = I/A indica il raggio di inerzia della sezione elevato al quadrato.
La condizione di progetto richiede σmax ≤ fyk, cioè
⎛
⎞
m
⎟⎟ ≤ A fyk,
N ⎜⎜1 +
⎝ 1 − N / N cr ⎠
(20)
Dividendo ambo i membri della (20) per Ncr, ed utilizzando la relazione (6)
ottenuta per la snellezza adimensionale λ si ottiene
N
N cr
⎛
m
⎜⎜1 +
⎝ 1 − N / N cr
⎞
⎟⎟ ≤ λ 2
⎠
E. Radi – Meccanica dei solidi e delle strutture, a.a. 2012-13
STABILITÀ DELL’EQILIBRIO
12
ovvero
2
N
⎛N ⎞
λ ⎜ cr ⎟ − 2 φ cr + 1 ≥ 0
N
⎝ N ⎠
2
(21)
dove
φ=
1
(1 + m + λ 2 )
2
(22)
La (21) risulta verificata con il segno di uguaglianza per la più piccola delle 2
radici ottenute dall’equazione di II grado (21) per il rapporto Ncr/N, cioè per
φ + φ2 − λ 2
N cr
=
N
λ2
(23)
Dalle (23) e (6) si ottiene
A f yk
N
1
=
N cr
φ + φ2 − λ2 N cr
per cui il coefficiente di riduzione per aste compresse in presenza di imperfezioni risulta
χ=
N
1
=
A f yk φ + φ 2 − λ2
(24)
Le norme tecniche (NTC, EC3) introducono poi un coefficiente di sicurezza γM1 =
1.05 sul materiale (che aumenta a 1.1 nel caso di ponti). Per cui la verifica di stabilità
delle aste compresse si esegue controllando che sia soddisfatta la condizione
N≤χ
A f yk
(25)
γM1
Il coefficiente di imperfezione generalizzata m definito dalle norme tecniche
dipende dalla snellezza dell’asta secondo la seguente relazione
⎧α ( λ − 0.2)
m=⎨
0
⎩
per
λ > 0 .2
per
λ ≤ 0.2
dove α è il fattore di imperfezione che dipende dal tipo di sezione e dalla direzione di
sollecitazione. In particolare, vengono definite 5 curve a cui corrispondono i seguenti
valori di α :
curva
a0
a
b
c
d
α
0.13
0.21
0.34
0.49
0.76
E. Radi – Meccanica dei solidi e delle strutture, a.a. 2012-13
STABILITÀ DELL’EQILIBRIO
13
coeff. di riduzione χ
1.2
1.0
0.8
0.6
a
b
0.4
χ = 12
λ
c
d
0.2
0.0
0 0.2
1
2
3
snellezza adimensionale λ
Per aste tozze di snellezza adimensionale λ ≤ 0.2 si ha m = 0 e quindi dalle (23) e
(24) segue χ = 1, per cui l’asta non è influenzata da fenomeni di instabilità. Mentre per
snellezze grandi, tutte le curve tendono all’iperbole di Eulero.
Le norme tecniche consentono quindi di riportare la verifica di stabilità ad una
verifica di resistenza mediante un’opportuna riduzione dello sforzo normale di progetto
attraverso il coefficiente di riduzione χ, il cui valore è definito in funzione di:
• tipo di sezione trasversale (legata alle imperfezioni geometriche e meccaniche).
• snellezza dell’elemento (legato al valore del carico critico);
• tipo di acciaio (legato al valore della tensione di snervamento fyk).
E. Radi – Meccanica dei solidi e delle strutture, a.a. 2012-13
STABILITÀ DELL’EQILIBRIO
E. Radi – Meccanica dei solidi e delle strutture, a.a. 2012-13
14