QUARTA LEZIONE: i triangoli
Riprendiamo la discussione dei sette punti in cui abbiamo suddiviso il Libro I di Euclide a partire dal
secondo punto.
Punto 2: primo criterio di uguaglianza dei triangoli
Il problema è che cosa determina un triangolo?
Ogni triangolo ha sei elementi: tre lati e tre angoli. Ma questi elementi non possono essere dati
indipendentemente l’uno dall'altro e ad arbitrio; se ne possono dare tre con certe limitazioni.
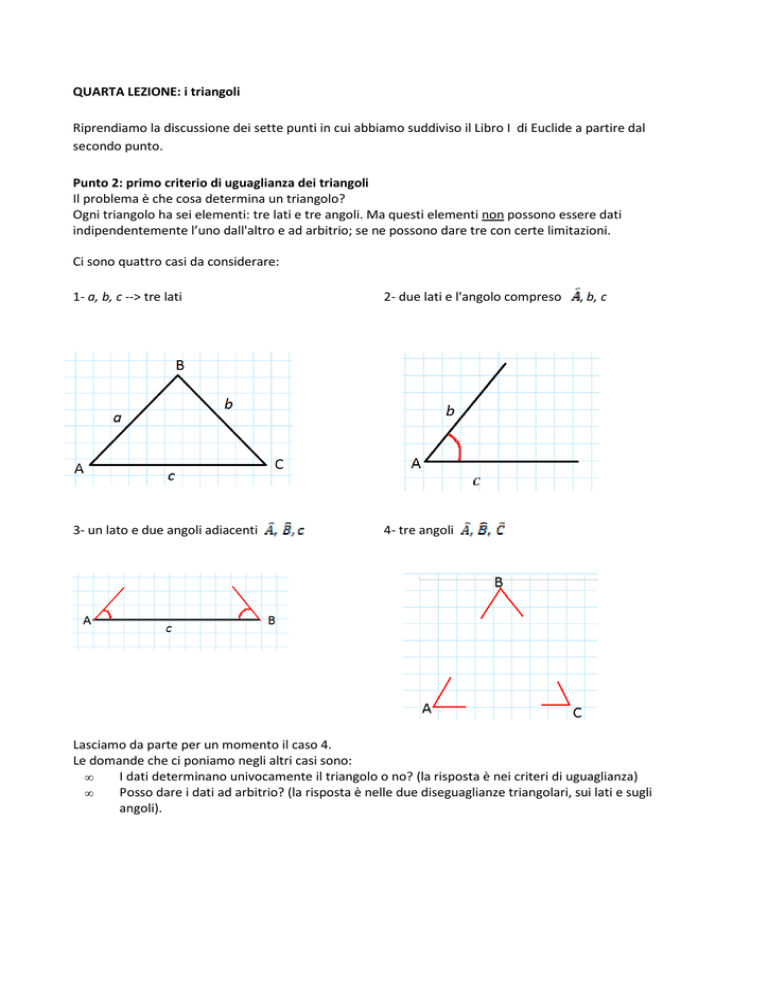
Ci sono quattro casi da considerare:
1- a, b, c --> tre lati
2- due lati e l'angolo compreso
3- un lato e due angoli adiacenti
4- tre angoli
, b, c
Lasciamo da parte per un momento il caso 4.
Le domande che ci poniamo negli altri casi sono:
I dati determinano univocamente il triangolo o no? (la risposta è nei criteri di uguaglianza)
•
Posso dare i dati ad arbitrio? (la risposta è nelle due diseguaglianze triangolari, sui lati e sugli
•
angoli).
Caso 2: due lati ed un angolo
Il caso 2 è il caso fondamentale (il punto di partenza dell'intera geometria euclidea).
Due ragioni:
1.
I dati ( , b, c) possono essere segnati ad arbitrio: non ci sono limitazioni, il triangolo esiste sempre;
2.
Questi dati sono sufficienti a determinare univocamente il triangolo.
L’univocità è fissata dal primo criterio di uguaglianza dei triangoli.
Primo criterio: due triangoli che abbiano due lati e l'angolo compreso uguali sono sovrapponibili ovvero
congruenti, e perciò hanno anche tutti gli altri elementi ordinatamente uguali.
Il primo criterio implica che gli altri tre elementi del triangolo (
, a) sono funzioni ben determinate
degli elementi assegnati: i due lati e l'angolo compreso ( , b, c). In particolare ciò è vero per il terzo lato
a . Il problema di sapere come a dipende da ( , b, c) è uno dei problemi centrali della geometria
euclidea. Qui c'è il legame con il teorema di Pitagora. Questo teorema specifica infatti la dipendenza del
lato a dagli elementi assegnati ne caso particolare in cui l’angolo
sia retto. Esso afferma che:
(attenzione: in questa formula bisogna scambiare a con c per essere coerenti con le notazioni
precedenti). Noi assumeremo il primo criterio come un postulato da aggiungere alla lista dei cinque
postulati elencati esplicitamente da Euclide.
Tutte le preposizioni che seguono saranno dedotte usando solo i cinque postulati di Euclide, il primo
criterio di uguaglianza dei triangoli e le cinque nozioni comuni.
Prima di iniziare il percorso che ci porterà al teorema di Pitagora, vediamo quali sono le conclusioni a cui
Euclide arriva in merito agli altri tre modi di assegnare un triangolo.
Caso 1: triangolo di tre lati assegnati
Euclide dimostra che:
1.
Non è possibile dare i tre lati ad arbitrio;
2.
I tre lati devono verificare le disuguaglianze triangolari, secondo cui in ogni triangolo ogni lato è
minore della somma degli altri due:
3.
Se sono verificate le tre disuguaglianze il triangolo esiste e tutti gli altri elementi del triangolo sono
univocamente determinati .
Vale infatti il terzo criterio di uguaglianza :
Due triangoli che abbiamo i lati corrispondenti uguali sono congruenti, cioè sovrapponibili , e i tre angoli
corrispondenti sono a coppie uguali.
Caso 3:un lato e due angoli adiacenti
Euclide dimostra che:
1.
Non è possibile dare i due angoli
ad arbitrio.
2.
I due angoli devono verificare la disuguaglianza
3.
che si enuncia dicendo che in ogni triangolo la somma di una qualsiasi coppia di angoli interni è
minore di due angoli retti.
Verificata questa disuguaglianza il triangolo esiste ed è unico.
Vale infatti il secondo criterio di uguaglianza:
Due triangoli che abbiano un lato e i due angoli adiacenti uguali sono congruenti, cioè sovrapponibili, e i
due lati rimanenti ed il terzo angolo sono a coppie uguali.
Caso 4: dati tre angoli
Se assegniamo soltanto i tre angoli il triangolo non è univocamente determinato. Esistono infiniti triangoli
che hanno i tre angoli uguali. Questi triangoli vengono detti simili perché godono della seguente proprietà
(che discende dal teorema di Talete)
a/a’ = b/b’ = c/c’ = k rapporto di similitudine.
I due triangoli non sono uguali, ma lo diventano se si ammette un cambiamento di scala (definito da k).
Punto 3: Pons asinorum
Cominciamo a percorrere la strada che porta dal primo criterio ai risultati prima discussi (gli altri due criteri
di uguaglianza, le disuguaglianze triangolari e i criteri di parallelismo).
Il primo passo è lo studio dei triangoli isosceli. Si tratta di dimostrare due proprietà importanti di questi
triangoli:
Gli angoli alla base sono uguali;
•
La bisettrice dell'angolo al vertice è anche mediana ed altezza relativa alla base.
•
Il primo risultato comincia a sviluppare un tema importante della geometria euclidea: la relazione tra lati ed
angoli opposti. Il teorema afferma che a lati uguali si contrappongano angoli uguali. Più avanti Euclide
dimostrerà una proprietà più forte: a lato maggiore si contrappone angolo maggiore.
Il secondo risultato ha un ruolo importante dal punto di vista costruttivo: insegna infatti a costruire con riga
e compasso
•
•
•
•
La bisettrice di un angolo;
Il punto medio di un segmento;
La perpendicolare ad una retta tracciata da un punto della retta;
La perpendicolare ad una retta tracciata da un punto fuori dalla retta.
Successivamente ci insegnerà anche a tracciare la parallela ad una retta data passante per un punto
assegnato non appartenenti alla retta.
Teorema: gli angoli alla base di un triangolo isoscele sono uguali
IPOTESI:
TESI:
DIMOSTRAZIONE: Si parte dalla seguente costruzione:
Con centri in B e C costruisco le conferenze di raggio BC: in questo modo
)
determino tre nuovi punti (
Si considera la prima coppia di triangoli ABG e ACF.
Questi triangoli hanno due lati uguali e l'angolo compreso uguale:
per ipotesi
12per costruzione in quanto
3-
perché è l'angolo al vertice del triangolo isoscele
Per il primo criterio gli altri tre elementi sono uguali. Dunque:
e soprattutto
Si considera poi la seconda coppia di triangoli BCF e BCG .
Questi due triangoli hanno due lati e l'angolo compreso uguale:
1per costruzione
23-
punto precedente
punto precedente
Per il primo criterio gli altri tre elementi sono uguali. In particolare sono uguali gli angoli in B e in C:
Conclusione:
riprendiamo il triangolo iniziale ABC,
ed osserviamo che gli angoli alla sua base sono
differenza di angoli uguali:
ABC = ABG - CBG
ACB = ACF - BCF
e quindi sono uguali.












