1
L'assoluto silenzio della vegetazione lungo
le sponde del fiume e il forte riverbero
prismatico quasi lo convincevano che la
Terra fosse ormai stata trasformata, avvolta
tutta in quella continua ed infinita ragnatela
di fili di cristallo scintillante e che la sua
marcia attraverso la foresta fosse ormai del
tutto inutile.
James G. Ballard, "La Foresta di Cristallo"
FIBRE OTTICHE
2
STRUTTURA E CLASSIFICAZIONE DELLE FIBRE OTTICHE
La fibra ottica in silice per le telecomunicazioni ha una
struttura tubolare a strati concentrici. A partire dal
centro si ha: il NUCLEO (Core) in silice amorfa e di
raggio a, il MANTELLO in silice amorfa (Cladding)
ed infine la GUAINA plastica opaca (Coating) che
isola otticamente la fibra dal mondo esterno.
Il nucleo centrale ed il cladding hanno diverso indice
di rifrazione: n1 per il nucleo ed n2 per il mantello.
Deve essere che
n1 > n2
Se all'interno del nucleo l'indice di rifrazione n1 si
mantiene uniforme dappertutto, allora si parla di STEP
INDEX FIBER (SIF).
Se invece l'indice di rifrazione n1 del nucleo dipende
dalla distanza dall'asse della fibra (dal raggio), essendo
massimo al centro, allora si parla di GRADED
INDEX FIBER (GIF).
Confronto tra i tre tipi principali di fibra ottica
3
PROPAGAZIONE DELLA LUCE NELLE FIBRE SIF MULTIMODALI
(MODELLO LINEARE)
All’interno della fibra, la luce si propaga per infinite riflessioni tra core e cladding se il
raggio è meridiano (ovvero giace su un piano passante per l’asse) e viaggia ad un angolo ,
rispetto all’asse, inferiore all’angolo critico dell’interfaccia tra i due materiali C [cos(C)=
n2/n1]. In tal caso si ha solo riflessione e niente rifrazione.
La luce non si propaga se l’angolo è maggiore dell’angolo critico (in tal caso il raggio si
estingue per multiple rifrazioni nel cladding) e se il raggio è sghembo, ovvero non giace su
un piano passante per l’asse.
Configurazione dei raggi sghembi
Nelle fibre GIF la traiettoria dei raggi è ricurva poiché, essendo l’indice di rifrazione nel core
massimo al centro e minimo alla interfaccia con il cladding, il raggio, attraversando i vari
gusci cilindrici della guida, è soggetto alla legge di Snell per cui tende a piegarsi con
continuità fino ad avere un andamento come quello in figura seguente.
4
AMBITI DI UTILIZZO DELLE FIBRE OTTICHE
Nella figura che segue viene illustrato in modo molto schematico la struttura di una rete di
comunicazioni telefoniche di una città o di un dato comprensorio amministrativo. La figura
va pensata in modo simmetrico con una altra o più città che ricevono o trasmettono
comunicazioni con la prima.
Lo schema illustra tutta una serie di utenti casalinghi connessi alla rete per mezzo di
collegamenti elettrici o ottici. Questa situazione è quella attuale in Italia in cui c'è ancora una
situazione ibrida tra link ottici ed elettrici. Il futuro tendenziale è quello di respingere sempre
più il confine tra elettrico ed ottico verso l'utente, cioè portare le fibre ottiche fin sull'uscio di
casa. In ogni caso questo schema è e sarà suddiviso in due diversi ambiti, distinti per
prestazioni, tecnologie usate e quantità di informazioni trasmesse:
la RETE DI ACCESSO e la RETE DI TRANSITO.
La RETE DI ACCESSO è formata da collegamenti tutti in ambito cittadino. E' strutturata ad
albero dove i diversi cabinet dove si affasciano insieme le informazioni, vanno pensati con
una gerarchia ( condominio, quartiere, distretto..) fino alla stazione TX-RX cittadina.
Man mano che dalla stazione cittadina si va verso i singoli utenti, le tratte di collegamento
diventano sempre più corte, la quantità di informazioni diminuisce ed aumenta
progressivamente il numero di utenti. Per queste ragioni man mano che si procede indietro
verso gli utenti, il costo degli impianti deve diminuire e bisogna usare tipi di fibre e
dispositivi fotonici poco costosi e quindi a basse prestazioni.
La RETE DI TRANSITO è costituita invece dall'insieme delle stazioni cittadine e dai
collegamenti ottici che le connettono. In questo ambito, che di fatto costituisce una super-rete
che collega le varie città principali del paese, si ha il massimo della quantità di informazioni
che transitano, le tratte di fibra senza ripetitore devono essere le più lunghe possibili mentre il
numero di stazioni è relativamente modesto. Per tutte queste ragioni nella rete di transito
vanno utilizzate fibre ottiche a larga banda trasmissiva e dispositivi fotonici a più alte
prestazioni e quindi più costosi. Soltanto in questa maniera si realizza l'obiettivo di
massimizzare da una parte la lunghezza di fibra senza bisogno di ripetitori e dall'altra
di massimizzare la quantità di informazioni trasmesse.
5
TECNOLOGIA DELLE FIBRE OTTICHE (CENNI)
Le fibre ottiche per le telecomunicazioni sono essenzialmente fatte di silice amorfa che non
ha una ben precisa temperatura di fusione ma possiede un intervallo di temperature in cui il
materiale da solido passa a liquido molto viscoso e successivamente diminuisce in modo
progressivo la viscosità.
Per questa ragione la fibra viene prodotta per mezzo di un processo di filatura a partire da un
modello (preform) della fibra stessa ma a scala maggiorata. Nelle due figure seguenti
vengono illustrati due metodi per costruire il preform da filare basati sulla tecnologia CVD
(Chemical Vapour Deposition).
Si parte in genere da un tubo di quarzo vuoto in cui vengono fatti scorrere i gas organici di
silicio (Silano SiCl4), ossigeno ed altri gas contenenti i droganti per variare l’indice di
rifrazione.
Nel MCVD (fig. in alto) un bruciatore si muove lentamente nella stessa direzione dei gas.
L’alta temperatura promuove la reazione dei gas facendo si che sulle pareti interne si depositi
una fuliggine (soot) di vetro direttamente a valle del bruciatore. Procedendo in avanti il
bruciatore provvede da una parte a vetrificare la fuliggine (rendendo il vetro privo di buchi e
bruciando via le impurezze organiche residue, e dall’altra a continuare a valle la deposizione
6
del soot. La procedura viene continuata fino a che il tubo si chiude interamente.
Il profilo di indice di rifrazione si ottiene modulando opportunamente tipo e concentrazione
dei gas contenenti i droganti. Nella variante della tecnica PMCVD ( fig. a pagina precedente
in basso) l'energia per la reazione chimica viene fornita da una radiofrequenza che produce un
plasma. Il bruciatore ha invece la sola funzione di trasformare il precipitato soot in vetro
compatto. Nella figura seguente si vede l’indice di rifrazione della silice in funzione di vari
tipi di drogante in grado di far aumentare o diminuire n in funzione della percentuale molare.
I droganti sono i medesimi utilizzati per drogare il silicio.
Schema dell’apparato per la filatura delle fibre ottiche a partire
da un modello a scala maggiorata (preform).
7
Nella figura in alto viene illustrato l’intero apparato per la filatura delle fibre ottiche a partire
da un preform.
Il mandrino in alto tende a far scendere progressivamente la barra di preform dentro la
fornace in cui il vetro diventa liquido e viene tirato in uscita sottoforma di fibra sottile.
Affinchè il processo sia continuativo è necessario che la divergenza del volume di materiale
all’interno della fornace sia nulla. Ovvero che sia valida l’equazione seguente.
(/4)*D2 * V = (/4) * d2 *v
Dove a primo membro viene indicato il volume entrante per unità di tempo mentre a secondo
membro il volume uscente per unità di tempo. V, v sono velocità, D, d i diametri.
La velocità di uscita v è quindi il parametro che deve essere regolato per controllare lo
spessore della fibra. Questo viene inoltre costantemente monitorato per mezzo di un
misuratore ottico. Segue poi una piccola fornace a bassa temperatura per la ricopertura con la
guaina in plastica.
Il tiraggio viene assicurato dalla macchina elettrica in basso: si tratta di un avvolgitore, la cui
velocità angolare di rotazione viene controllata in modo fine per mantenere costante la
velocità periferica v con cui la fibra viene tirata man mano che aumenta la quantità di filo
avvolta.
INNESCO DELLA LUCE ALL’INTERNO DELLA FIBRA
Per quanto detto, i raggi di luce all'interno della fibra si propagano per riflessioni multiple
all'interfaccia tra core e cladding se il loro angolo è minore dell'angolo critico c. Raggi con
angoli maggiori hanno una parte rifratta nel cladding e quindi si estinguono dopo alcune
riflessioni.
Facendo riferimento alla figura sopra, la condizione di propagazione corrisponde alla
condizione che sulla faccia piana della fibra il raggio entri con un angolo minore o uguale a
o detto angolo di innesco. Applicando la legge di Snell (versione coi seni) alla interfaccia
tra core e vuoto, si ha:
8
1 * sen(o) = n1 sen(c)
;
sen(o) = n1* (1 – n22/n12)1/2 = (n12 – n22)1/2 = NA
Quindi il seno dell'angolo di accettazione è detto Apertura Numerica NA ed è uno dei
parametri caratteristici della fibra.
CALCOLO DELLA POTENZA INNESCATA IN FIBRA: CASO DI SORGENTE
LAMBERTIANA
Nella figura successiva si vede in modo schematico una sorgente luminosa (un LED)
Il LED in pratica è un dischetto coassiale con la fibra in cui tutti i punti del dischetto hanno
un diagramma di irradiazione di tipo lambertiano.
Tale diagramma, inteso come la quantità di potenza infinitesima emessa dal punto per unità di
angolo solido e per unità di area del punto, ha la seguente espressione in funzione delle
coordinate polari (angolo di declinazione) e (angolo di rotazione attorno all'asse
orizzontale).
B(,) = Bo cos ()
dove Bo è il valore massimo per
Nella stessa figura per confronto è riportato il diagramma di irradiazione di una sorgente
molto più direttiva (Laser DFB).
Tornando alla distribuzione lambertiana, la porzione di potenza utile per la trasmissione della
luce in fibra P è costituita dalla potenza contenuta all'interno del cono di semi apertura o.
Per ottenere questa quantità è necessario integrare la funzione B(,) dapprima all'interno di
tale cono, poi sulla intera superficie emittente del LED intesa come un disco piatto di raggio
rm, ed avente anch'esso coordinate polari r e
Si tenga presente che la porzione infinitesima di angolo solido è d = sen() dd
mentre la porzione infinitesima dell'area della sorgente è dA = r dr d
9
Il risultato della integrazione multipla è il seguente:
P = 2 rm2 Bo sen2(o) mentre l'intera potenza del LED è PTOT = 2 rm2 Bo
Quindi la potenza P che si innesca in fibra è data da
P = PTOT*sen2(o) = PTOT *NA2
Il quadrato dell'apertura numerica è di fatto il rendimento di accoppiamento tra sorgente e
fibra o efficienza di accoppiamento.
In realtà le cose possono andare anche peggio di così. Infatti il calcolo si è fatto nella ipotesi
che il raggio del core a sia molto maggiore del raggio del led rm. Nel caso che questo non
avvenga, ovvero l'area del LED sia maggiore dell'area del core della fibra, il rendimento
peggiora di un fattore a2/rm2
A questa iattura si aggiungano gli effetti del disallineamento e disassamento tra fibra e
sorgente che diminuiscono ulteriormente la potenza utile innescata perché si vengono a creare
una molteplicità di raggi sghembi.
Da quanto detto e tenuto conto che la differenza percentuale tra gli indici di rifrazione del
core e del cladding si aggira sull'1% per le fibre multimodali e dello 0.1% per quelle
monomodali, si comprende come la bassa potenza innescabile in fibra sia un problema
oltremodo spinoso a cui bisogna porre rimedio perché è uno dei fattori che limita la
lunghezza massima utilizzabile per la fibra, soprattutto per quella monomodale.
Le strategie per risolvere il problema sono tre.
1)
Al posto del LED si utilizza un dispositivo LASER a semiconduttore con diagramma
molto più direttivo in modo da far capitare la maggior parte della potenza all'interno
dell'angolo di innesco. Questa è una soluzione obbligatoria per le fibre monomodali.
10
2)
L'angolo di innesco si aumenta artificialmente per mezzo di micro-lenti convergenti,
opportunamente integrate sulla sorgente, sulla terminazione della fibra o poste in mezzo,
come viene illustrato nella figura seguente.
3)
Si inserisce, appena dopo l'innesco della luce in fibra un preamplificatore a fibra di
erbio EDFA che, per quanto bassa possa essere la potenza che si è innescata, questa viene
notevolmente amplificata per compensare le attenuazioni, allungando quindi la massima
lunghezza di fibra utilizzabile. Questa soluzione è stata adottata solo in tempi recenti (metà
anni 90) quando si sono resi disponibili gli amplificatori EDFA.
11
SPIEGAZIONE DELL’ORIGINE DEI MODI DI PROPAGAZIONE SECONDO
L’OTTICA LINEARE
Da quanto detto finora sembrerebbe che la propagazione in fibra sia garantita dal fatto che
l’angolo di innesco del raggio di luce all’interno del core della fibra sia minore dell’angolo
critico e che quindi tutti gli angoli di innesco permessi formino un insieme continuo tra 0 e
c. Così non è. !
La propagazione dei raggi di luce in fibra deve essere uguale a quella nello spazio libero.
Deve cioè sottostare all’assunto seguente: preso un piano equifase, se ci si sposta nel verso di
propagazione ad una distanza arbitraria, il nuovo piano deve essere ancora un piano equifase.
Questo vuol dire propagazione dell’onda.
Facendo riferimento alla figura seguente, l’assunto implica che la fase nel punto A (poco
prima della riflessione) e quella nel punto C (poco prima della riflessione) devono essere
uguali a meno di multipli interi dell’angolo giro.
A causa del fatto che in corrispondenza dei punti di riflessione si ha una discontinuità di fase
pari a che dipende dall'angolola condizione non è verificata per tutti gli angoli ma
soltanto per un insieme discreto che verifica la formula.
C - A = 2 n1 Ko d / sen(1) + 2 m
I valori di angolo di innesco 1 per cui è verificata la formula si dicono angoli di
congruenza, i quali coincidono con altrettanti modi di propagazione.
L’intervallo che comprende gli angoli di congruenza è tra 0 e c, chiuso a sinistra e aperto a
destra: ovvero l’angolo =0 appartiene sicuramente all’insieme (ed è detto modo
fondamentale), mentre non è affatto detto che l’angolo =c vi appartenga.
12
COSTANTI DI PROPAGAZIONE ASSIALE DEI MODI
Ai fini della propagazione dell’informazione lungo la fibra, quello che interessa non è la
costante di propagazione del singolo modo nella direzione i, bensì la sua proiezione lungo
l’asse della fibra i (costante di propagazione assiale). Ora a causa delle rotazioni di fase
aggiuntive nei punti di riflessione si ha:
i ≠ n1 Ko cos (i)
Quindi i valori delle costanti di propagazione assiale non sono calcolabili con la semplice
trigonometria ma costituiscono un insieme di autovalori tabellati che discendono dalla
risoluzione delle equazioni di Maxwell. I valori di i sono compresi tra n1Ko (per il modo
fondamentale) ed n1Ko cos(c) = n2Ko.
INDICE DI RIFRAZIONE MODALE o DI GUIDA
Ora da un punto di vista puramente ingegneristico conviene trasferire la ‘tabellarità’ dalle
costanti di propagazione assiale all’indice di rifrazione. Cioè si pone :
n1 Ko cos (i) ≠ i = ng Ko
dove il parametro fittizio ng viene detto indice di rifrazione modale o di guida.
Sono quindi ora gli indici di rifrazione ad essere tabellati. I vari valori di n g sono compresi tra
n1 (per il modo fondamentale) ed n2.
L’operazione che si è fatta è tutta mentale, ovvero così facendo ci si può comodamente
dimenticare di essere in una guida pensando di essere invece nello spazio illimitato. Si può
pensare che il modo propagativo in fibra corrisponda ad una propagazione dell’onda in uno
spazio non guidato con indice di rifrazione ng.
Distribuzione discreta dei vari parametri associati ai modi propagativi.
Gli intervalli sono chiusi a sinistra e aperti a destra.
13
I MODI DI PROPAGAZIONE SECONDO LE EQUAZIONI DI MAXWELL
Sezione longitudinale degli andamenti del campo elettrico per il modo fondamentale
e per i primi due modi superiori.
In una guida d'onda metallica il campo elettrico relativo ai modi di propagazione deve
necessariamente sottostare alla condizione al contorno nulla ai bordi della guida perchè il
campo elettrico non può penetrare all'interno del metallo. In una guida dielettrica non esiste
questo vincolo.
Ne consegue che nella fibra la configurazione di campo elettrico propria dei modi di
propagazione si estende sia nel core che nel cladding, come si può vedere nella figura di
sopra, per il modo fondamentale e per i primi due modi superiori.
In particolare per tutti i modi nel cladding l'andamento è evanescente esponenziale negativo
all'aumentare del raggio mentre è di tipo armonico all'interno del core.
La velocità di propagazione del modo (anche quello fondamentale) non corrisponde a quello
relativo all'indice di rifrazione del core n1, ma deve avere un valore mediato tra n1 ed n2 in
proporzione alla ripartizione di potenza che viaggia nel core e nel cladding.
Quindi, contrariamente a quanto stabilito in precedenza, neanche il modo fondamentale ha un
fattore di propagazione assiale pari a n1 Ko l'indice di guida non è mai pari ad n1 ed il b è
sempre minore di 1.
Sezione longitudinale degli andamenti del campo elettrico per il modo fondamentale
in una distanza di fibra pari a g.
14
La distribuzione del campo elettrico in ogni sezione della fibra si muove in modo armonico
(come una corda di chitarra) passando per tutte la configurazioni illustrate nella figura
precedente per il modo fondamentale. Naturalmente, fissando il tempo, la distribuzione del
campo elettrico si ripete uguale a se stessa ad una distanza pari a g.
Sezione longitudinale degli andamenti del vettore di Poynting per il modo fondamentale
e per i primi due modi superiori.
La configurazione del vettore di Poynting
(punto per punto dato dal prodotto vettore tra
campo elettrico e campo magnetico) relativo
al modo di propagazione è costante in ogni
sezione della fibra. La figura precedente in
alto illustra le configurazioni del vettore di
Poynting per il modo fondamentale e per i
primi due modi superiori.
Nella figura a fianco sono invece illustrate le
linee di flusso del campo elettrico (linee
continue) e magnetico (linee tratteggiate)
nella sezione trasversale della fibra per il
modo fondamentale, (in alto e per altri tre
modi superiori.
15
I GRAFICI CARATTERISTICI DELLA FIBRA
I due grafici nella figura precedente sono i grafici caratteristici della fibra SIF. Essi
riassumono in se tutte le proprietà della propagazione dei modi in funzione dei parametri
costitutivi della fibra. Essi sono estremamente importanti in quanto consentono di risolvere
tutte le problematiche progettuali inerenti alla guida.
Il parametro della ascissa, comune a entrambi i grafici, è la frequenza normalizzata V,
parametro che congloba tutti gli altri dati (a raggio del core, o lunghezza d'onda, NA
apertura numerica):
2a
2a
2
2 ½
V = ---------- (n1 – n2 ) = ---------- NA
oo
Tutte le curve nei due grafici si riferiscono ai vari modi di propagazione: quello marcato con
01 è quello relativo al primo modo fondamentale che è definito per ogni valore di V. Tutte le
curve successive al modo fondamentale partono da un valore di V maggiore di zero che è
detto frequenza di taglio del modo. In particolare la frequenza di taglio del secondo modo
superiore è pari a V = 2.405.
Quindi per ottenere una fibra SIF monomodale è necessario impostare raggio del core e
apertura numerica in modo che la frequenza normalizzata sia minore di tale valore.
L'ordinata del primo grafico è il parametro b costante di propagazione assiale
normalizzata, data da:
(/Ko)2 - n22
b = -----------------n12 - n22
(/Ko) - n2
ng - n2
~ ------------------- = ----------n1 - n2
n1 - n2
la quale è compresa tra 0 ed 1. Naturalmente questo grafico potrebbe avere come ordinata
16
l'indice di rifrazione modale o di guida ng, che sarebbe compreso tra n2 ed n1.
Si noti che la condizione b = 1 è una condizione asintotica cioè anche per il modo
fondamentale non è mai vero che l'indice di rifrazione di guida sia uguale a n 1, ovvero che la
costante di propagazione assiale sia uguale a n1 Ko.
Il secondo grafico a destra indica per ogni modo di propagazione e per ogni valore di V il
parametro Pclad/Ptot, la frazione di potenza del modo che viaggia nel cladding rispetto
alla potenza totale. Si vede che, essendo tutte le curve monotone decrescenti, all'aumentare di
V tende ad aumentare la potenza che viaggia nel core e a diminuire la potenza che viaggia nel
cladding.
Si ribadisce ancora l'importanza di questi grafici in quanto consentono di risolvere tutti i
quesiti e le problematiche concernenti le fibre SIF multimodali e monomodali.
A titolo di esempio e di esercizio, il candidato risponda ai seguenti quesiti facendo uso dei
grafici caratteristici.
Una fibra con V = 6 , quanti modi propagativi Risposta
supporta?
Si vuole realizzare una fibra monomodale Risposta
con la potenza che viaggia prevalentemente
nel core. Quale è l'intervallo di V che devo
usare? (si risolva graficamente ).
In una fibra monomodale realizzata per la Risposta
lunghezza d'onda ocon V=1.6, devo inserire
un'altra luce con 1. Quale è il minimo valore
di 1 per cui la fibra è ancora monomodale
per entrambi i colori?
17
LE PATOLOGIE DELLA FIBRA :
LA DISPERSIONE TEMPORALE DEGLI IMPULSI
Come illustrato nella figura a lato, la
dispersione temporale degli impulsi consiste nel
progressivo allargamento della loro larghezza
man mano che gli impulsi stessi procedono
lungo la lunghezza della fibra.
Quindi se vengono iniettati due impulsi ben
separati temporalmente tra loro, il loro
progressivo allargamento fa si che essi si
fondano tra loro, fino a diventare totalmente
irriconoscibili come impulsi distinti.
La ragione risiede nel fatto che il singolo
impulso di luce, per varie ragioni, è composto
da componenti che viaggiano lungo la fibra con
diverse velocità. Tali componenti, pur partendo insieme, arrivano una dopo l’altra
provocando un allargamento temporale dell’impulso.
La dispersione si divide in : dispersione multimodale e dispersione monomodale o
cromatica. Quella monomodale a sua volta si divide in dispersione naturale e dispersione
di guida.
DISPERSIONE MULTIMODALE
Nelle fibre multimodali, l’energia degli impulsi si distribuisce tra i vari modi di
propagazione. Questi, come si è visto viaggiano nel nucleo della fibra con angoli diversi per
cui percorrono la lunghezza L della fibra in tempi diversi.
L’effetto di allargamento dell’impulso per dispersione multimodale è almeno due ordini di
grandezza maggiore di quella dispersione cromatica. Per questo cui nelle fibre multimodali,
in cui c’è ugualmente la dispersione cromatica, quest’ultima in genere viene trascurata.
Volendo dare una valutazione grossolana approssimata per eccesso dell’allargamento
dell’impulso tg in questo caso, si suppone che a) la velocità della luce nei modi corrisponda
a quella relativa all’indice di rifrazione n1 nel nucleo, b) il modo maggiore corrisponda a
quello con angolo di congruenza pari all’angolo critico e c) si ignorino le rotazioni di fase alle
riflessioni.
L n1
L n1
tg = tempo più lungo – tempo meno lungo = ------------- - ------------ =
c cos(c)
c
tg = (L * n1 / c) * (n1/n2 – 1)
Tale valore è solo una maggiorazione grossolana. In realtà l’allargamento dell’impulso è
molto minore non solo perché non sono vere le ipotesi a), b) e c), ma anche per la ragione che
verrà spiegata nella parte relativa all’attenuazione della fibra.
18
DISPERSIONE MONOMODALE o CROMATICA
La dispersione temporale che avviene nelle fibre monomodali viene detta cromatica perché
ha origine nel fatto che la sorgente luminosa non ha uno spettro infinitamente coerente ma
possiede una molteplicità di lunghezze d’onda distribuite in modo continuo. Ogni lunghezza
d’onda possiede una sua propria velocità con cui percorre la fibra per due ragioni: a) l’indice
di rifrazione della silice dipende dalla lunghezza d’onda (dispersione naturale) secondo il
grafico riportato in seguito e b) ciascuna lunghezza d’onda ha in fibra il suo particolare valore
di ng indice di rifrazione di guida (dispersione di guida).
Essendo tg il tempo di percorrenza dell’impulso di luce
lungo l’intera lunghezza L della fibra, il parametro D
dispersione monomodale si definisce come segue:
1
d tg
D = ---- * ------L
d o
Il parametro D che deve essere fornito dal costruttore
serve in pratica al progettista a calcolare l’allargamento
dell’impulso ( e quindi la massima frequenza di bit f max
utilizzabile in fibra). Infatti passando ai rapporti
incrementali si ha
1/fmax = tg = L * D *
Dove è la larghezza dello spettro della luce in termini
Grafico dell’indice di rifrazione della di lunghezza d’onda.
silice in funz. Della lunghezza d’onda.
Poiché il valore della dispersione cromatica è in genere contenuto, i due contributi D mat e Dwg
rispettivamente della dispersione materiale e di guida, si calcolano separatamente e poi si
sommano, come in una sorta di sovrapposizione degli effetti. Per la dispersione materiale si
assumono nulli gli effetti della guida, come se l’onda viaggiasse nello spazio non confinato
con indice di rifrazione n(). Per la dispersione di guida si ignora la dipendenza da lambda
dell’indice di rifrazione mentre si tiene conto della dipendenza da lambda della costante di
propagazione assiale normalizzata b.
Per il calcolo di entrambi i contributi si parte dalla definizione della velocità di gruppo
dell’impulso.
tg 1 ng 1 d
o 2 d
L vg c c dKo
2 c d o
Per il calcolo della dispersione materiale si pone:
19
2 n( o)
o
Mentre per la dispersione di guida si pone.
n 2 Ko (b 1)
con
( n1 n2) / n1
Come risultato si ha che la dispersione materiale D mat dipende dalla derivata seconda di n(o)
rispetto a o mentre la dispersione di guida Dwg è costante ed indipendente dalla lunghezza
d’ondama dipendente dal raggio del core della fibra, per lo meno nell’intervallo di frequenze
normalizzate interessate dalle guide monomodali.
DMAT
o d 2 n( o)
c
d o2
La figura seguente illustra i grafici della dispersione materiale, della dispersione di guida per
due diversi valori del raggio del core e della dispersione totale nei due casi, in funzione della
lunghezza d’onda.
Si può notare che la dispersione materiale ( che non si può modificare) si annulla dove n()
possiede un flesso a 1.3 microns (coincidente con la II finestra di attenuazione delle fibre in
silice). L’effetto della equalizzazione con la dispersione di guida fa in modo di spostare a
maggiori lunghezze d’onda il valore in cui la dispersione totale è nulla. Questo in pratica
spiega la convenienza ad utilizzare la III finestra di attenuazione per le trasmissioni a lunga
20
distanza. Infatti in questo range di lunghezze d’onda è possibile progettare fibre a dispersione
nulla, scegliendo un valore opportuno per il raggio del core. Naturalmente questo
accorgimento non si può adottare ne per la I che per la II finestra di attenuazione.
FIBRE MULTICLADDING
Se all’interno della finestra di attenuazione debbono viaggiare più portanti ottiche, è
opportuno che la fibra sia a zero dispersione nell’intero intervallo di ampiezza della III
finestra e non soltanto in un solo valore . Per questa ragione si usano delle fibre multi
cladding, in cui l’indice di rifrazione nel cladding è modulato in modo complicato. Queste
fibre hanno la proprietà di avere in parte la dispersione di guida dipendente dalla lunghezza
d’onda. In questo modo la somma della dispersione di guida e della dispersione naturale
tende ad annullarsi in un intero intervallo di lunghezze d’onda in corrispondenza della III
finestra di attenuazione a 1.55 microns. La figura seguente illustra questo comportamento.
Effetto sulla dispersione totale delle fibre multi-cladding. L’inserto illustra
un possibile andamento dell’indice di rifrazione in funzione del raggio della fibra.
BANDA DELLE FIBRE
In relazione alle proprietà della dispersione, le fibre sono classificate per valore della banda
B. Questo parametro, le cui dimensioni sono [Mhz*Km], definisce la massima frequenza di
bit utilizzabile per 1 Km di fibra. Quindi per avere la massima frequenza utilizzabile f max per
una fibra lunga L, si ha:
fmax = B / L
I valori tipici per le varie fibre sono :
fibre SIF multimodali 20-40 Mhz*Km;
fibre GIF multimodali 500 Mhz*Km;
fibre SIF monomodali 1-10 Ghz*Km;
21
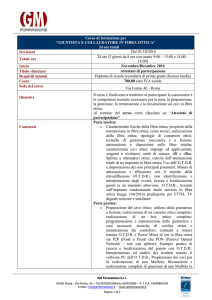
LE PATOLOGIE DELLA FIBRA :
L’ATTENUAZIONE
L'attenuazione della potenza luminosa che viaggia in fibra viene misurata in
decibel/chilometro.
Le cause principali dell'attenuazione sono tre, ciascuna delle quali è suddivisa in sottocause:
Assorbimento, Scattering,
Perdite radiative.
Assorbimento: si verifica quando l'evento comporta la scomparsa del fotone e la cessione
della sua energia al reticolo cristallino.
Si dice Assorbimento Intrinseco quando le cause riguardano la matrice dell'ossido di silicio
di cui è composta la fibra, per cui sono sostanzialmente ineliminabili.
Si dice invece Assorbimento Estrinseco quando le cause coinvolgono le impurezze o i
droganti all'interno della matrice dell'ossido.
Nell'assorbimento intrinseco è incluso quello Elettronico, quando l'energia del fotone è
sufficientemente ampia (circa da 6 eV in su) da consentire la ionizzazione di un elettrone di
valenza nella banda di conduzione dell'ossido il quale si libera e passa nella banda di
conduzione dell'ossido. Questo tipo di assorbimento si verifica nella banda degli ultravioletti.
L'assorbimento intrinseco Fononico riguarda la collisione tra un fotone (tipicamente nella
banda degli infrarossi) ed un fonone, ovvero con le oscillazioni del reticolo cristallino dovute
alla temperatura. L'energia del fotone che scompare va ad aumentare l'energia interna del
reticolo e quindi la sua temperatura. L'influenza è scarsa nel Vicino Infrarosso NIR mentre
comincia ad essere marcata a partire da 2 microns di lunghezza d'onda in su, nella banda del
lontano infrarosso FIR. L'Assorbimento Fononico genera la parete destra del grafico
dell'attenuazione Vs lunghezza d'onda. L'assorbimento intrinseco Fononico è una causa
praticamente ineliminabile.
Formalmente a cavallo tra l'assorbimento intrinseco e quello estrinseco è quello causato dai
22
radicali OH che sono rimasti nella matrice dell'ossido dalla formazione del materiale. Come
ben si sa, questa impurezza ha un legame assai debole e per giunta l'energia in grado
ionizzare il legame si colloca in lunghezza d'onda proprio in mezzo alla banda NIR, causando
due picchi di assorbimento che separano proprio le tre tradizionali finestre di attenuazione a
0,85 microns, a 1.3 microns ed a 1.55 microns. Fino a qualche tempo fa questi due picchi
erano considerati ineliminabili. Tuttavia di recente si sono messe in atto delle innovative
tecniche di gettering (purificazione) che consentono o di eliminare completamente l'idrogeno
residuo o di sostituirlo co il Fluoro che forma un legame molto più forte. In entrambi i casi
non avrebbe più senso parlare di tre distinte finestre di attenuazione ma il grafico
dell'attenuazione avrebb un unica larga finestra dal fondo piatto da 0,8 a 2,0 microns di
lunghezza d'onda.
L'assorbimento Estrinseco è causato da una collisione tra un fotone ed un atomo di
impurezza nel reticolo, voluto nel caso dei droganti usati per modificare l'indice di
rifrazione, oppure non voluto. Naturalmente l'effetto di attenuazione è direttamente
proporzionale alla concentrazione di drogante nella fibra.
23
Scattering: si verifica quando l'evento non comporta la scomparsa del fotone ma la
deviazione della sua normale traiettoria. La 'collisione' avviene tra il fotone ed una
disomogeneità locale del materiale (concentrazione anomala di silicio oppure buchi o voids
nel reticolo) che provoca una variazione locale dell'indice di rifrazione la quale si comporta
come una sorta di microlente.
Si suddivide in Scattering Normale, quando le dimensioni della anomalia sono maggiori
della lunghezza d'onda del fotone e Diffusione di Raleigh, quando le dimensioni sono
confrontabili con la lunghezza d'onda del fotone.
Nello Scattering Normale si ha proprio una deviazione del fotone dalla sua usuale traiettoria.
Nella Diffusione di Raleigh invece il centro colpito dal fotone diventa una fonte di
irradiazione dell'energia uniforme sull'angolo giro. E' il tipico fenomeno che spiega il cielo
azzurro sulla terra e rosso su marte (vedi dispensa sui fondamenti della luce). Questo
fenomeno è inversamente proporzionale alla quarta potenza della lunghezza d'onda; nelle
fibre è prevalente nella banda degli UV e supera di gran lunga il contributo dell'assorbimento
elettronico. La parete sinistra del grafico dell'assorbimento nelle fibre è dunque dovuto al
contributo della Diffusione di Raleigh.
NOTA:
Lo Scattering Normale è l'unico fenomeno, tra tutti quelli che provocano l'effetto
indesiderato dell'attenuazione, che ha un effetto collaterale parzialmente benefico: è in
grado di ridurre la dispersione nelle fibre multimodali anche drasticamente.
Infatti se un fotone appartenente ad un determinato modo di propagazione caratterizzato da
un angolo di congruenza collide con un centro di scattering, avrà un angolo di uscita che, se
è maggiore dell'angolo critico provoca la perdita del fotone per trasmissione nel cladding, se
è minore dell'angolo critico vuol dire che il fotone passa da un modo propagativo ad un altro
con velocità diversa.
Quindi i fotoni appartenenti ai modi, per effetto dello scattering passano continuamente da un
modo all'altro per cui le velocità di percorrenza sono mediate ed i tempi di percorrenza della
fibra da parte dell'impulso tendono ad equalizzarsi, per cui l'impulsostesso si allarga di meno.
Nel grafico bilogaritmico seguente viene illustrato l'allargamento dell'impulso in funzione
della distanza L per diversi valori di h ovvero della concentrazione lineare di centri di
scattering per unità di lunghezza di fibra (Km -1). Si vede che tanto maggiore è h, tanto più
precoce e marcato è l'insorgere della equalizzazione dei tempi.
24
Perdite Radiative. Le perdite radiative si verificano in corrispondenza dalle curvature
della fibra, prprio in virtù del fatto che i modi di propagazione prevedono una parte della
potenza del modo che viaggia nel cladding.
Normalmente la velocità del modo ha un valore di compromesso tra quella massima nel
cladding e quella massima nel core. In corrispondenza della curva, se si dovesse mantenere
l'integrità del modo di propagazione la potenza che viaggia nel cladding esternamente alla
curvatura dovrebbe accelerare mentre quella che viaggia internamente dovrebbe rallentare,
proprio accade quando come un plotone di soldati a più righe deve curvare mantenendo
intatta la formazione. Siccome questo non è possibile, allora nelle curve si verificano delle
perdite di potenza, tanto più marcate quanto minore è il raggio di curvatura. Questo problema
non è per nulla banale nei casi di cavi di fibre molto lunghi che di fatto subiscono minipiegamenti anche a causa dello stress meccanico che interviene durante la fase di deposizione
del cavo.
Meccanismo delle perdite radiative in corrispondenza delle curvature della fibra
FIBRE AD INDICE GRADUALE (CENNI)
Le fibre ad indice graduale (GIF) sono progettate in modo da avere una banda di valore
intermedio (500 Mhz Km) tra la SIF multimodale e la SIF monomodale. Il loro utilizzo è
nell'ambito della rete di accesso, in quelle tratte distanti dall'utente che necessitano di una
maggiore lunghezza e maggiore quantità informativa trasmessa. Il profilo dell'indice nel core
a
ærö
n(r ) = n1 × 1 - 2D ç ÷
èaø
n( r ) = n 2
per r < a
per r ³ a
n12 - n 2 2
con D =
2n12
25
a essendo il parametro che regola la curvatura del profilo di indice. Per a grande il profilo
della GIF tende a quello della SIF.
Le ragioni per cui la banda della fibra è aumentata rispetto alla SIF multimodo risiedono
sostanzialmente in una minore dispersione multimodale. Le ragioni sono molteplici.
1)
A causa del percorso ricurvo dei raggi di luce all'interno della fibra, a parità di angolo
di congruenza di innesco, il percorso del raggio nella GIF è inferiore a quello che avviene
nella SIF multimodale per riflessioni multiple.
2)
Visto che l'indice di rifrazione è massimo in corrispondenza dell'asse centrale della
fibra il raggio ricurvo viaggia per la maggior parte del percorso in una zona a minore indice
di rifrazione e quindi viaggia più velocemente.
3)
A parità di frequenza normalizzata V, il numero di modi permessi nella GIF è inferiore
a quello della SIF se il parametro a che regola la curvatura è minore di 3.
Lo svantaggio non indifferente è che l'apertura numerica della GIF dipende dal valore
dell'indice di rifrazione n(r) in corrispondenza dell'asse della sorgente. Quindi nelle GIF è
tassativo curare molto l'aspetto della coassialità tra fibre e sorgente.
Se si considerano insieme gli effetti della dispersione multimodale e di quella cromatica, si
vede che esiste un valore di a che minimizza la dispersione. Il grafico seguente illustra
l'allargamento dell'impulso per unità di lunghezza di fibra in funzione del parametro a e per
tre tipi di emettitori a diversa banda spettrale: LED, Laser a guida di guadagno e Laser DFB
(il più coerente).
Da grafico si può intuire che, al fine di minimizzare la dispersione, bisogna tentare di
realizzare il valore di a ottimo, ma non è conveniente usare un Laser DFB costoso, in quanto
un piccolo errore su a causerebbe un grande aumento della dispersione. La scelta migliore per
pilotare una fibra GIF a minima dispersione è dunque un laser a guida di guadagno.