geometria

Annamaria Viceconte
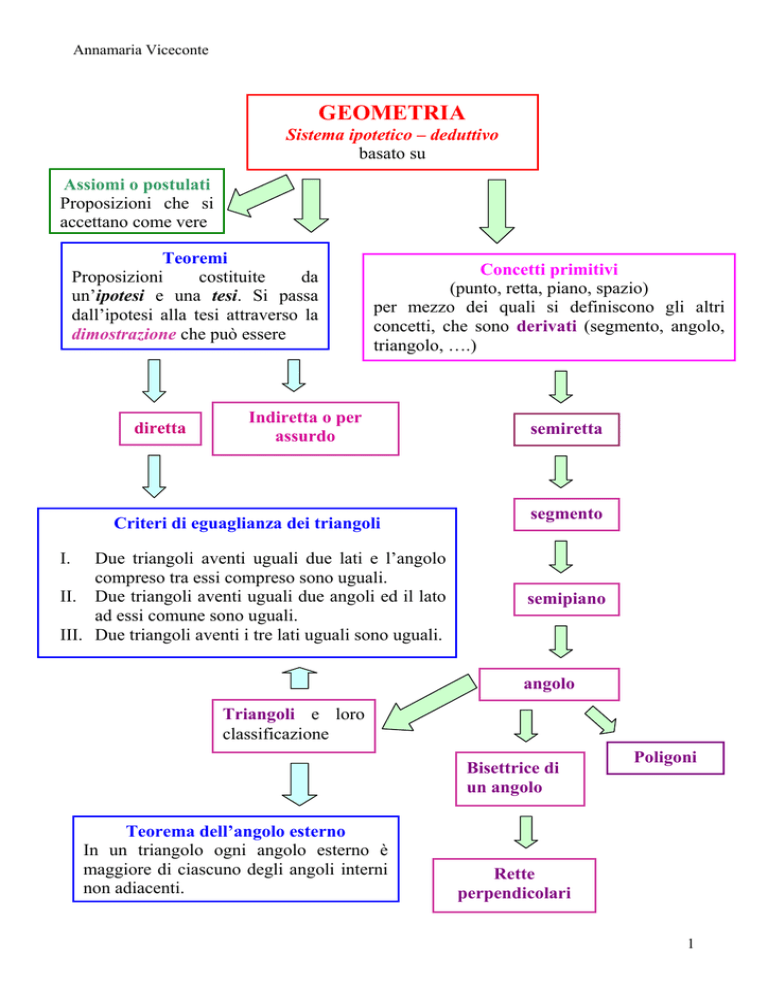
GEOMETRIA
Sistema ipotetico – deduttivo
basato su
Assiomi o postulati
Proposizioni che si
accettano come vere
Teoremi
Proposizioni
costituite
da
un’ipotesi e una tesi. Si passa
dall’ipotesi alla tesi attraverso la
dimostrazione che può essere
diretta
Concetti primitivi
(punto, retta, piano, spazio)
per mezzo dei quali si definiscono gli altri
concetti, che sono derivati (segmento, angolo,
triangolo, ….)
Indiretta o per
assurdo
Criteri di eguaglianza dei triangoli
Due triangoli aventi uguali due lati e l’angolo
compreso tra essi compreso sono uguali.
II. Due triangoli aventi uguali due angoli ed il lato
ad essi comune sono uguali.
III. Due triangoli aventi i tre lati uguali sono uguali.
semiretta
segmento
I.
semipiano
angolo
Triangoli e loro
classificazione
Bisettrice di
un angolo
Teorema dell’angolo esterno
In un triangolo ogni angolo esterno è
maggiore di ciascuno degli angoli interni
non adiacenti.
Poligoni
Rette
perpendicolari
1
Annamaria Viceconte
Bisettrice di
un angolo
Triangoli e loro
classificazione in
relazione ai lati
(scaleno, isoscele,
equilatero)
Triangoli e loro
classificazione
in
relazione agli angoli
Triangoli rettangoli e
loro proprietà
Triangolo isoscele
e
proprietà
Teorema
I. In un triangolo isoscele gli
angoli alla base sono eguali.
e il suo inverso
II. Se in un triangolo gli angoli alla
base sono eguali allora il
triangolo è isoscele.
Rette
perpendicolari
Asse di un segmento
Teorema
Ogni punto dell’asse di un
segmento è equidistante
dagli estremi del segmento
e viceversa.
Teorema
In un triangolo isoscele la
bisettrice dell’angolo al vertice è
perpendicolare alla base (altezza)
e la divide in due parti eguali
(mediana).
2
Annamaria Viceconte
Rette parallele
V postulato di Euclide
Data una retta e un punto non
appartenente ad essa, esiste una e una
sola retta passante per il punto dato
parallela alla retta data.
Definizione
Due rette sono parallele
quando, essendo complanari,
non hanno punti in comune.
Il parallelismo come
relazione di equivalenza
Cenni alle geometrie
non euclidee
Angoli formati da due rette qualsiasi
tagliate da una trasversale
Condizione necessaria e sufficiente affinché due rette tagliate da una
trasversale siano parallele è che formino:
o angoli alterni (interni, esterni) uguali
o angoli corrispondenti uguali
o angoli coniugati (interni, esterni) supplementari.
Teorema
La somma degli angoli
interni di un triangolo è un
angolo piatto.
Teorema
In un triangolo con due
lati disuguali, anche gli
angoli opposti sono
disuguali;
a
lato
maggiore si oppone
angolo maggiore e
viceversa.
Teorema
Ogni lato di un triangolo
è minore della somma
degli altri due e maggiore
della loro differenza.
3
Annamaria Viceconte
Poligoni
Teorema
La somma degli angoli interni
di un poligono convesso è
uguale a tanti angoli piatti
quanti sono i lati meno due; la
somma degli angoli esterni è
sempre un angolo giro.
Quadrilateri
Parallelogramma
Quadrilatero con i lati
opposti paralleli
Trapezio
Quadrilatero con due
lati paralleli
Parallelogrammi
particolari
Rombo
Parallelogramma con
quattro lati uguali
Proprietà
Rettangolo
Parallelogramma con
quattro angoli retti
Quadrato
Parallelogramma con i
lati uguali e gli angoli
retti
4
Annamaria Viceconte
Circonferenza
Insieme dei punti del piano aventi una stessa
distanza da un punto fissato
Corde e diametri
Proprietà
Teorema
In una circonferenza:
- corde uguali hanno dal
centro stessa distanza e
viceversa;
- corde maggiori hanno
dal centro distanza
minore e viceversa.
Cerchio
Figura convessa formata da
una circonferenza e da tutti
i suoi punti interni
Angoli al centro
e angoli alla
circonferenza
Settore circolare
Intersezione tra un cerchio
e un angolo al centro
Teorema
Ogni angolo al centro
è
doppio
dei
corrispondenti angoli
alla circonferenza
Segmenti circolari a una
e due basi
Corona circolare
Intersezione
tra
due
circonferenze concentriche
Per un punto passano infinite circonferenze.
Per due punti passano infinite circonferenze
Teorema
Per tre punti non allineati passa una e una sola
circonferenza
Posizioni retta e circonferenza
Teorema
- se una retta ha dal centro distanza minore
del raggio essa è secante la circonferenza;
- se una retta ha dal centro distanza eguale
al raggio essa è tangente alla
circonferenza;
- se una retta ha dal centro distanza
maggiore del raggio essa è esterna alla
circonferenza.
Teorema inverso
Se una retta è, rispettivamente, secante,
tangente, esterna ad una circonferenza, la
sua distanza dal centro è minore, uguale o
maggiore del raggio
Posizioni relative di due circonferenze
Due circonferenze possono essere:
- esterne l’una all’altra;
- tangenti internamente o esternamente;
- secanti;
- interne l’una all’altra.
Corollario
La perpendicolare a un qualsiasi
raggio di una circonferenza è
tangente alla circonferenza nel
suo punto di contatto; vale il
viceversa.
5
Annamaria Viceconte
Misura
Le figure geometriche sono misurabili se appartengono ad una classe completa
di grandezze omogenee (sono omogenee, sono confrontabili, è possibile
stabilire un criterio per sommarle)
I segmenti se sono isometrici hanno la stessa
lunghezza e la stessa misura rispetto ad un
segmento preso come unità di misura
Gli angoli se sono isometrici hanno la
stessa ampiezza e la stessa misura rispetto
ad un angolo preso come unità di misura
La misura è un numero reale:
- razionale ⇒ le grandezze sono
commensurabili
- irrazionale ⇒ le grandezze sono
incommensurabili (diagonale e lato
di un quadrato)
I poligoni
Se hanno la stessa estensione
(concetto primitivo) sono
equivalenti
Teorema
Se due poligoni possono scomporsi
in uno stesso numero di parti fra loro
isometriche essi sono equivalenti o
equiscomponibili.
Due poligoni equiscomponibili
hanno la stessa area
Teorema
Ogni poligono è equiscomponibile con
un triangolo o con un rettangolo.
Teorema
- Un parallelogramma è equivalente ad
un rettangolo con stessa base e stessa
altezza.
- Un triangolo è equivalente ad un
parallelogramma con metà base e stessa
altezza.
- Un trapezio è equivalente ad un
triangolo con uguale altezza e base uguale
alla somma delle basi.
Primo teorema di Euclide – Teorema
di Pitagora – Secondo teorema di
Euclide
6
Annamaria Viceconte
Proporzionalità e Similitudine
Due classi di grandezze si dicono direttamente proporzionali se esiste fra
esse una corrispondenza biunivoca tale che il rapporto fra due qualsiasi di
grandezze della prima classe è uguale al rapporto delle corrispondenti della
seconda.
Teorema
Condizione necessaria e sufficiente perché due
classi di grandezze siano direttamente
proporzionali è che il rapporto fra la misura di
una qualsiasi grandezza della prima classe e la
misura della corrispondente grandezza della
seconda sia costante.
Teorema di Talete
Un fascio di rette parallele
stacca sopra due trasversali
segmenti corrispondenti in
proporzione.
Due triangoli si dicono simili quando hanno gli angoli
ordinatamente uguali e i lati corrispondenti in proporzione.
I criterio di similitudine
dei triangoli
Due triangoli aventi gli
angoli uguali sono simili.
II criterio di similitudine
dei triangoli
Due triangoli aventi un
angolo uguale e i lati che lo
comprendono in proporzione
sono simili.
III criterio di similitudine
dei triangoli
Due triangoli aventi i lati
in proporzione sono simili.
I teorema di Euclide
In un triangolo rettangolo un cateto è medio
proporzionale fra l’ipotenusa e la proiezione
del cateto stesso sull’ipotenusa.
Teorema di Pitagora
In un triangolo rettangolo l’area del
quadrato costruito sull’ipotenusa è
uguale alla somma delle aree dei
quadrati costruiti sui singoli cateti.
II teorema di Euclide
In un triangolo rettangolo l’altezza
relativa
all’ipotenusa
è
media
proporzionale fra i due segmenti in cui il
suo piede divide l’ipotenusa.
7