DM8

La maledizione della dimensionalità
!!
!!
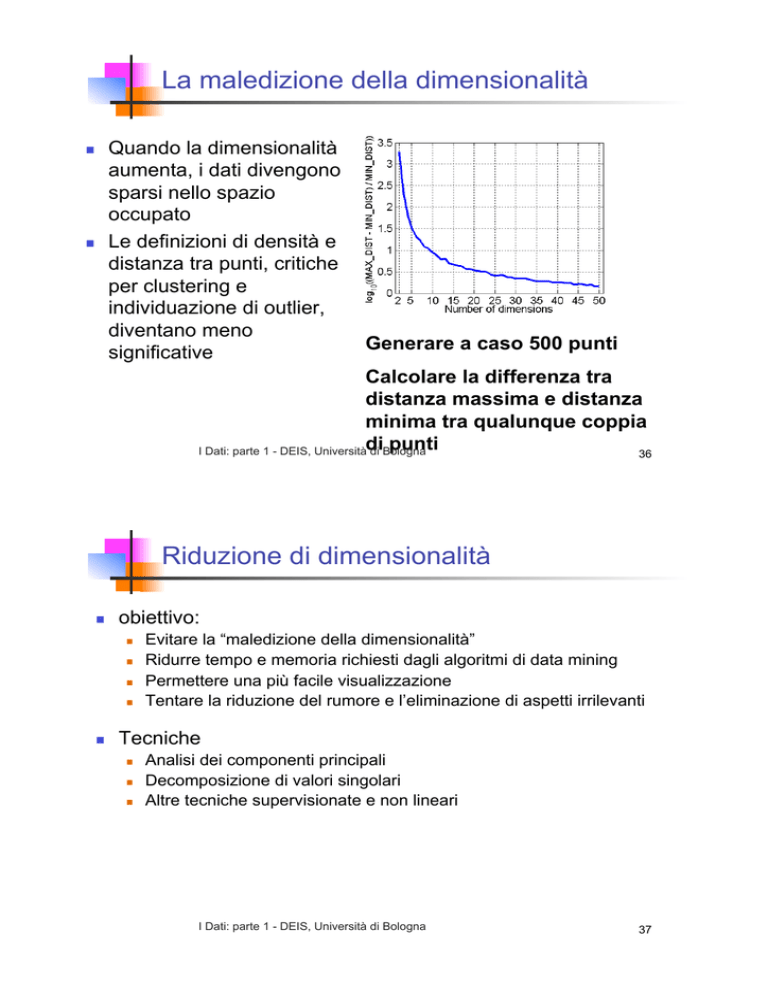
Quando la dimensionalità
aumenta, i dati divengono
sparsi nello spazio
occupato
Le definizioni di densità e
distanza tra punti, critiche
per clustering e
individuazione di outlier,
diventano meno
•!Generare a caso 500 punti
significative
•!Calcolare la differenza tra
distanza massima e distanza
minima tra qualunque coppia
punti
I Dati: parte 1 - DEIS, Universitàdi
di Bologna
36
Riduzione di dimensionalità
!!
obiettivo:
!!
!!
!!
!!
!!
Evitare la “maledizione della dimensionalità”
Ridurre tempo e memoria richiesti dagli algoritmi di data mining
Permettere una più facile visualizzazione
Tentare la riduzione del rumore e l’eliminazione di aspetti irrilevanti
Tecniche
!!
!!
!!
Analisi dei componenti principali
Decomposizione di valori singolari
Altre tecniche supervisionate e non lineari
I Dati: parte 1 - DEIS, Università di Bologna
37
Riduzione di dimensionalità:
PCA (principal components analysis)
!!
!!
!!
nuova proiezione in uno spazio cartesiano con meno
dimensioni che catturi la massima variazione dei dati
il primo asse è la variabile con la maggiore varianza, il
secondo asse con la seconda var. a maggiore varianza etc.
metodo non supervisionato
!!x2
!!e
I Dati: parte 1 - DEIS, Università di Bologna
!!x1
38
Riduzione di dimensionalità: ISOMAP
!! Tenenbaum, de Silva,
Langford (2000)
!!
!!
!!
Costruire un grafo di vicinanza
Per ogni coppia di punti nel grafo, calcolare le distanze
minime
Ridefinire le distanze come somme di percorsi tra vicini
I Dati: parte 1 - DEIS, Università di Bologna
39
Selezione di un sottoinsieme di attributi
!!
Attributi ridondanti
!!
!!
!!
Duplicano gran parte delle informazioni contenute in uno o più degli
altri attributi
Esempio: prezzo di acquisto e importo dell’iva
Attributi irrilevanti
!!
!!
attributi ad elevata o bassa variabilità non contengono informazioni
utili per il data mining
Esempio: codici fiscali, partita iva, codici di prodotto etc.
I Dati: parte 1 - DEIS, Università di Bologna
40
Selezione di un sottoinsieme di attributi (ii)
!!
Tecniche:
!!
Forza bruta:
!!
!!
Approcci “embedded”:
!!
!!
La selezione è intrinseca all’algoritmo di data mining
Filtraggio:
!!
!!
Provare tutti i possibili sottoinsiemi di attributi
Selezione a monte dell’algoritmo di data mining
Approcci “Wrapper”:
!!
Uso dell’algoritmo di data mining come una scatola nera per trovare il
migliore sottoinsieme di attributi
I Dati: parte 1 - DEIS, Università di Bologna
41
Creazione di attributi
!!
!!
I nuovi attributi possono catturare le informazioni importanti
del data set in modo più efficiente di quelli originali
Tre metodologie generali:
!!
Estrazione di “features”
!!
a)!
b)!
"!
!!
Mappare i dati in un nuovo spazio
!!
!!
esempio: riconoscere se un’immagine contiene un viso
Analizzare i pixel
Analizzare la presenza di linee caratteristiche della presenza di un viso
Fortemente legato al dominio
Esempio: trasformate di Fourier per mettere in evidenza aspetti temporali
Costruzione di attributi
!!
Esempio: sostituire massa e volume di oggetti con la densità
I Dati: parte 1 - DEIS, Università di Bologna
42
Mappare dati in un nuovo spazio
!! Fourier
!! Wavelet
!!Due
sinusoidi
!!Due sinusoidi
con rumore
I Dati: parte 1 - DEIS, Università di Bologna
!!Analisi nel
dominio delle
frequenze
43
Discretizzazione
!!
Trasformare dati continui in categorici
!!
Ridurre il numero di categorie se eccessivo
!!
Certi algoritmi lavorano meglio con dati categorici
!!
Trasformare dati discreti in attributi binari (binarizzazione)
!!
Necessario trovare la discretizzazione migliore
I Dati: parte 1 - DEIS, Università di Bologna
44
Discretizzazione non supervisionata
!!Dati originali
Equi-ampiezza
!!Equi-frequenza
I Dati: parte 1 - DEIS, Università di Bologna
!!K-means
45
Discretizzazione supervisionata
!!
!!
!!
Su più dimensioni contemporaneamente
Quando sono disponibili informazioni supplementari sulle
“classi” degli oggetti
Ottenere la massima “purezza” delle partizioni
!!
!!
In generale crea overfitting
!!
!!
!!
# minimizzare entropia
il test set non può essere discretizzato in questo modo poiché i valori
dell’attibuto target/classe si suppongono ignoti
Metodo valido: filtro (e.g. discretizzazione) supervisionata
solo del training set e applicazione del risultato al test set
in WEKA: usare un Metalearner che combina l’algoritmo di
learning con il filtro (e.g. discretizzazione)
!!
usare FilteredClassifier dalla sezione Meta del panel Classify
(pulsante Choose) per scegliere un classificatore ed un filtro
I Dati: parte 1 - DEIS, Università di Bologna
46
Discretizzazione supervisionata (ii)
!!3 categorie per x e y
!!5 categorie per x e y
I Dati: parte 1 - DEIS, Università di Bologna
47
ancora sulla riduzione degli attributi
!!
!!
gli attributi irrilevanti deteriorano l’efficacia e l’efficienza della
gran parte degli algoritmi di data mining
due metodi:
!!
!!
!!
Esempi con uso di machine learning:
!!
!!
!!
!!
applicare al data set un decision tree (cross-validation)
selezionare dal data set solo gli attributi usati nell’albero calcolato
applicare al data set un algoritmo diverso dai decision tree
Altro esempio:
!!
!!
riduzione a partire dalle caratteristiche dei dati (non automatica)
impiego di algoritmi di machine learning
individuare un sottoinsieme di attributi che individualmente si
correlano bene con l’attributo classe/target ma con bassa intercorrelazione tra loro
Metodi iterativi più sofisticati basati sul ranking degli attributi
I Dati: parte 1 - DEIS, Università di Bologna
48
riduzione attributi con metodi di ricerca
!!
!!
!!
!!
obiettivo: individuare il sottoinsieme degli attributi che più
probabilmente predice meglio l’attributo target/classe
la ricerca in questo spazio è esponenziale rispetto al numero
degli attributi
riduzione della complessità cercando in modo greedy in una
o due direzioni, forward selection & backword elimination
forward selection
!!
!!
!!
backward elimination
!!
!!
aggiunta di un attributo a turno e test con cross-validation per stimare
l’efficacia del nuovo sottoinsieme
la ricerca termina quando nessun attributo produce un miglioramento
procede in modo analogo ma al contrario partendo dall’intero data set
ed eliminando un attributo alla volta
metodi più sofisticati (forward & backword, best-first search, beam,
I Dati: parte 1 - DEIS, Università di Bologna
algoritmi genetici)
49
Trasformazione di attributi
!!
Valori di un attributo #nuovo insieme di valori con
corrispondenza biunivoca
!!
!!
!!
xk, log(x), ex
Standardizzazione e Normalizzazione
Esempio:
!!
!!
!!
!!
Persone descritte con età e reddito
differenze di reddito >> differenze di età
# analisi dominate dal reddito
Standardizzazione
!!
X’ = (X – media(X)) / devStandard(X)
I Dati: parte 1 - DEIS, Università di Bologna
50
Similarità e Dissimilarità
!!
Similarità
!!
!!
!!
!!
Dissimilarità
!!
!!
!!
!!
!!
Misura numerica riferita a due oggetti
Aumenta con la somiglianza
Generalmente [0,1]
Misura numerica riferita a due oggetti
Diminuisce con l’aumentare della somiglianza
Minimo generalmente 0
Massimo può variare
Prossimità
I Dati: parte 1 - DEIS, Università di Bologna
51
similarità/Dissimilarità per attributi semplici
Tipo di attributo
Dissimilarità
#0 se
d=$
%1 se
Nominale
p=q
p"q
n Valori mappati in interi
[0,n-1]
Ordinale
p"q
d= !
n "1
!
Similarità
#0 se
d=$
%1 se
p"q
s = 1"
n "1
s = "d
s=
1
1+ d
s = e"d
d = p"q
Intervallo o rapporto
d " min(d)
max(d) " min(d)
In generale, la conversione s/d si può fare con qualunque funzione
monotona decrescente
!
!!
p"q
p=q
!
!
s = 1"
I Dati: parte 1 - DEIS, Università di Bologna
!
52
Distanza euclidea
!!
!!
!!
n = numero di dimensioni (attributi )
pk e qk = k-esimi componenti di p e q
Se le scale differiscono occorre standardizzare
I Dati: parte 1 - DEIS, Università di Bologna
53
Distanza euclidea (ii)
!!Matrice delle distanze
I Dati: parte 1 - DEIS, Università di Bologna
54
Distanza di Minkowski
!!
Generalizzazione della distanza euclidea
!!
r è un parametro
I Dati: parte 1 - DEIS, Università di Bologna
55
Distanza di Minkowski: esempi
!!
r = 1. City block (Manhattan, taxicab, L1 norm)
!!
Esempio: distanza di Hamming, numero di bit diversi in due vettori
binari
!!
r = 2. distanza euclidea
!!
r ! ". “supremum” (Lmax norm, L" norm)
!!
!!
Massima differenza tra componenti dei vettori
Tutte queste distanze sono definite per qualsiasi numero di
dimensioni
I Dati: parte 1 - DEIS, Università di Bologna
56
Distanza di Minkowski
!!Matrici delle distanze
I Dati: parte 1 - DEIS, Università di Bologna
57
Matrice delle covarianze
!!
!!
!!
!!
Variazione di coppie di variabili aleatorie
Sommatoria, estesa al numero di osservazioni n, dei
quadrati delle differenze tra una componente di
un’osservazione e le medie di tutte le altre componenti
I valori della diagonale principale sono le varianze
!ij > 0 se i valori delle componenti i e j tendono a crescere
insieme nelle osservazioni
1 n
" ij = $ (x hi # µ j ) 2
n h=1
I Dati: parte 1 - DEIS, Università di Bologna
58
!
Distanza di Mahalanobis
!!# è la matrice di covarianza
dei dati di input X
!!per i punti rossi la distanza euclidea è 14.7, la distanza di Mahalanobis è 6.
I Dati: parte 1 - DEIS, Università di Bologna
59
Distanza di Mahalanobis (ii)
!!La congiungente A e C è “in
direzione” della correlazione
! la distanza “vale meno” di
quella tra A e B
!!Matrice di
covarianza:
!!
C
!!A: (0.5, 0.5)
!!
B
!!B: (0, 1)
!!
A
!!C: (1.5, 1.5)
!!Mahal(A,B) = 5
!!Mahal(A,C) = 4
I Dati: parte 1 - DEIS, Università di Bologna
60
Proprietà comuni di una distanza
!!
!!
!!
d(p, q) $ 0 per ogni p e q e
d(p, q) = 0 solo se p = q (positività)
d(p, q) = d(q, p) per ogni p e q (simmetria)
d(p, r) % d(p, q) + d(q, r) per ogni punto p, q, e r
(disuguaglianza triangolare)
!!
!!
d(p, q) è la distanza (dissimilarità) tra punti (oggetti dati), p e q.
Una distanza che soddisfa le proprietà sopra è definta una
“metrica”
I Dati: parte 1 - DEIS, Università di Bologna
61
Esempi di distanze non metriche
!!
Differenza di insiemi
!!
d(A,B) = |A-B|
!!
!!
!!
!!
Non soddisfa la seconda parte della positività (vale zero anche se B
contiene più elementi di A, quindi per B diverso da A)
Non soddisfa la simmetria
D(A,B) = |A-B| + |B-A| è una metrica
Differenza tra orari del giorno
!!
!!
Se un evento si verifica alle 13 di ogni giorno e sono le 14, fra quanto
tempo si verificherà?
d(13,14) = 1
d(14,13) = 23
I Dati: parte 1 - DEIS, Università di Bologna
62
Proprietà comuni di una similarità
!!
s(p, q) = 1 (massima similarità) solo se p = q.
!!
s(p, q) = s(q, p) per ogni p e q. (simmetria)
!!
s(p, q) è la similarità tra punti (oggetti dati), p e q.
I Dati: parte 1 - DEIS, Università di Bologna
63
Similarità tra vettori binari
!!
!!
!!
!!
!!
!!
!!
M01 = numero di attributi in cui p è 0 e q è 1
M10 = numero di attributi in cui p è 1 e q è 0
M00 = numero di attributi in cui p è 0 e q è 0
M11 = numero di attributi in cui p è 1 e q è 1
Coefficienti Simple Matching (SMC) e Jaccard (J)
SMC = numero di concordanze / numero di attributi
= (M11 + M00) / (M01 + M10 + M11 + M00)
J = numero di concordanze 11 / numero di valori “non
entrambi zero”
= (M11) / (M01 + M10 + M11)
I Dati: parte 1 - DEIS, Università di Bologna
64
SMC versus Jaccard: esempio
!!
!!
!!
!!
!!
!!
!!
!!
p= 1000000000
q= 0000001001
M01 = 2
M10 = 1
M00 = 7
M11 = 0
(numero di attributi in cui p è 0 e q è 1)
(numero di attributi in cui p è 1 e q è 0)
(numero di attributi in cui p è 0 e q è 0)
(numero di attributi in cui p è 1 e q è 1)
SMC = (M11 + M00)/(M01 + M10 + M11 + M00) = (0+7) /
(2+1+0+7) = 0.7
J = (M11) / (M01 + M10 + M11) = 0 / (2 + 1 + 0) = 0
I Dati: parte 1 - DEIS, Università di Bologna
65
Similarità coseno
!!
se d1 e d2 sono due vettori ”documento”, allora
cos( d1, d2 ) = (d1 • d2) / ||d1|| ||d2|| ,
dove • il prodotto scalare || d || è la norma del vettore d.
!!
esempio:
!!
!!
!!
!!
d1 = 3 2 0 5 0 0 0 2 0 0
d2 = 1 0 0 0 0 0 0 1 0 2
!!
d1 • d2= 3*1 + 2*0 + 0*0 + 5*0 + 0*0 + 0*0 + 0*0 + 2*1 + 0*0 + 0*2 = 5
||d1|| = (3*3+2*2+0*0+5*5+0*0+0*0+0*0+2*2+0*0+0*0)0.5 = (42) 0.5 = 6.481
||d2|| = (1*1+0*0+0*0+0*0+0*0+0*0+0*0+1*1+0*0+2*2) 0.5 = (6) 0.5 = 2.245
!!
cos( d1, d2 ) = .3150
!!
!!
I Dati: parte 1 - DEIS, Università di Bologna
66
Coefficiente di Jaccard esteso (Tanimoto)
!!
Variazione di Jaccard per attributi continui o conteggio
!!
Si riduce a Jaccard per attributi binari
I Dati: parte 1 - DEIS, Università di Bologna
67
Correlazione
!!
!!
Misura la relazione lineare tra oggetti
Standardizza gli oggetti e le esegue il prodotto vettoriale
I Dati: parte 1 - DEIS, Università di Bologna
68
Valutazione visuale della correlazione
!!Diagrammi di
dispersione per
similarità
da –1 a 1.
I Dati: parte 1 - DEIS, Università di Bologna
69
Scegliere la giusta misura di prossimità
!!
!!
Dipende dai dati
Densi, continui
"!
!!
Dati sparsi, asimmetrici
!!
!!
!!
Misure metriche come la distanza euclidea
Coseno, Jaccard, Jaccard esteso
Trasformazioni e normalizzazioni
Tenere conto delle eventuali trasformazioni di uso comune
nel dominio sotto considerazione
I Dati: parte 1 - DEIS, Università di Bologna
70
Combinare più modelli -> più accuratezza
!!
!!
!!
combinare le decisioni di più modelli per ottenere una
decisione finale più accurata
motivazione: diversi training set presi nello stesso dominio
producono modelli anche molto diversi
Bagging
!!
!!
!!
!!
!!
meccanismo del voto a maggioranza (dati nominali)
valore medio (dati numerici)
tutti i voti (dei modelli) pesano allo stesso modo
esiste in weka
Boosting
!!
!!
!!
come Bagging, ma i voti pesano in modo diverso a seconda
dell’accuratezza individuale
in weka AdaBoost.M1
metodi Isimili
Additive
ClassificationViaRegression
Dati: parte
1 - DEIS,regression,
Università di Bologna
71
Usare i dati non etichettati
!!
!!
spesso i dati etichettati/classificati sono pochi perché il costo
per produrli può essere elevato
co-training
!!
!!
!!
!!
!!
due data set con lo stesso obiettivo di learning (e.g. contenuto di
pagine web e pagine web con link entranti nelle precedenti)
apprendere i due modelli separatamente dal data set etichettato
applicare il modello ai data set non etichettati
rimuovere dai data set non etichettati le due osservazioni con
predizioni positive e negative migliori
aggiungere le due osservazioni ai data set etichettati e ripetere il
procedimento fino ad esaurire i dati non etichettati
I Dati: parte 1 - DEIS, Università di Bologna
72