Principali Funzioni del Data Mining

1
Data Mining
Corso di
Metodi e Modelli per il Supporto alle Decisioni
a.a. 2002-03
2
KDD e Data Mining - Introduzione (1)
• Crescita notevole degli strumenti e delle tecniche per generare e
raccogliere dati (introduzione codici a barre, transazioni economiche
tramite carta di credito, dati da satellite o da sensori remoti, servizi on
line..)
• Sviluppo delle tecnologie per l’immagazzinamento dei dati, tecniche di
gestione di database e data warehouse, supporti piu’ capaci piu’
economici (dischi, CD) hanno consentito l’archiviazione di grosse quantita’
di dati
• Simili volumi di dati superano di molto la capacità di analisi dei metodi
manuali tradizionali, come le query ad hoc. Tali metodi possono creare
report informativi sui dati ma non riescono ad analizzare il contenuto dei
report per focalizzarsi sulla conoscenza utile.
3
KDD e Data Mining - Introduzione (2)
• Emerge l'esigenza di tecniche e strumenti con la capacità di assistere in
modo intelligente e automatico gli utenti decisionali nell'estrazione di
elementi di conoscenza dai dati.
• Queste tecniche e strumenti sono al centro del campo emergente del
Knowledge Discovery in Databases (KDD).
• Il termine knowledge discovery in databases, o KDD, indica l'intero
processo di ricerca di nuova conoscenza dai dati
• Il termine di data mining si riferisce all'applicazione di algoritmi per estrarre
pattern dai dati senza considerare gli ulteriori passi che caratterizzano il
processo di KDD (come, ad esempio, incorporare appropriata conoscenza
a priori e fornire una opportuna interpretazione dei risultati).
4
KDD e Data Mining - Introduzione (3)
• Pertanto l'intero processo, tipicamente interattivo e iterativo, di ricerca,
estrazione ed interpretazione di pattern dai dati, che indichiamo come
KDD, coinvolge l'applicazione ripetuta di specifici metodi e algoritmi di
data mining e l'interpretazione dei pattern generati da tali algoritmi.
• Nel seguito forniremo una definizione più dettagliata di KDD e una
panoramica sui metodi e gli algoritmi di data mining più usati
5
Il processo di KDD (1)
Interpretation/
Evaluation
Application Domain
Prior Knowledge
User’s Goals
Knowledge
Data Mining
Patterns
Transformation
Preprocessing
……
……
……
Selection
Transformed
Data
Preprocessed
Data
Metadata
Target Data
Data
6
Il processo di KDD (2)
1) Sviluppo e approfondimento del dominio di applicazione, della
conoscenza disponibile a priori e degli obiettivi dell'utente finale.
2) Creazione di un target data set: selezione del data set o focalizzazione
su un sottoinsieme di variabili o di campioni di dati oggetto del processo
KDD.
3) Cleaning dei dati e preprocessing: operazioni di base come la rimozione
del rumore o degli outliers se è il caso, raccolta delle informazioni
necessarie per modellare o tener conto del rumore, messa a punto di
strategie per gestire i dati mancanti e per gestire i dati tempo-varianti.
4) Riduzione dei dati e proiezione: rappresentazione dei dati in modo
opportuno in relazione agli obiettivi della ricerca. Riduzione delle
dimensioni e impiego di metodi di trasformazione per ridurre l'effettivo
numero di variabili da sottoporre al processo di ricerca.
7
Il processo di KDD (3)
5) Scelta del compito del processo di data mining: identificazione
dell'obiettivo del KDD, se si tratti di una classificazione, di una
regressione, di un clustering…
6) Scelta dell'algoritmo o degli algoritmi di data mining: selezione dei metodi
da usare per ricercare pattern nei dati. Questa fase comprende la
decisione su quali modelli e parametri potrebbero essere appropriati e il
matching di un particolare metodo di data mining con i criteri generali del
processo KDD (per es. l'utente finale potrebbe essere maggiormente
interessato alla comprensione del modello piuttosto che alle sue capacità
predittive).
8
Il processo di KDD (4)
7) Data mining: ricerca di pattern di interesse in una particolare forma di
rappresentazione o su un set di rappresentazioni diverse (regole di
classificazione, alberi decisionali, regressione, clustering…). Il risultato
del processo di data mining è considerevolmente influenzato dalla
correttezza delle fasi precedenti.
8) Interpretazione dei pattern trovati e possibile ritorno alle fasi 1-7 per
ulteriori iterazioni.
9) Consolidamento della conoscenza estratta: incorporazione di tale
conoscenza nel sistema di performance o, semplicemente,
documentazione e reporting alle parti interessate. Questa fase include
anche il controllo per la risoluzione di potenziali contraddizioni con la
conoscenza precedentemente disponibile.
9
Data Mining - Introduzione
I due principali obiettivi di alto livello del data mining sono la predizione e
la descrizione.
•
La predizione implica l'uso di variabili o campi di un database per predire
valori ignoti o futuri di altre variabili di interesse.
•
La descrizione si concentra invece sulla ricerca di pattern interpretabili che
descrivano i dati.
L'importanza relativa di predizione e descrizione nelle diverse applicazioni
del data mining può variare considerevolmente. Nel contesto del KDD la
descrizione tende ad essere più importante della predizione, mentre nelle
applicazioni di pattern recognition e machine learning (per es. speech
recognition) la predizione spesso costituisce l'obiettivo principale
10
Principali Funzioni del Data Mining (1)
•
Classificazione: consiste nell'apprendere una funzione che mappa
(classifica) un elemento in una tra molte classi predefinite.
•
Regressione: consiste nell'apprendere una funzione che mappa un
elemento in una variabile predittiva a valori reali.
La classificazione si distingue dalla regressione per il tipo di output che
fornisce.
Con la classificazione, l’output predetto (l’appartenenza ad una classe) è
di tipo categorico, cioè assume pochi valori, tipo “Si’” o “No”, oppure
“Basso”, “Medio” o “Alto”.
La regressione invece prevede come output un valore numerico che può
assumere un numero illimitato (o almeno molto grande) di possibili valori.
La classificazione costituisce, insieme alla regressione, il tipo di problema
più comune a cui viene applicato il data mining.
11
Principali Funzioni del Data Mining (2)
•
Clustering: è un task a carattere tipicamente descrittivo in cui si cerca di
identificare un numero finito di categorie o cluster per descrivere i dati.
Tali categorie possono essere mutuamente esclusive ed esaustive oppure
possono fornire una rappresentazione più ricca con categorie gerarchiche
o parzialmente sovrapposte.
•
Aggregazione: le tecniche di aggregazione comprendono metodi per la
ricerca di descrizioni compatte per sottoinsiemi di dati. Un esempio
semplice potrebbe essere la tabulazione della media e della deviazione
standard per tutti i campi. Metodi più sofisticati comprendono la
derivazione di regole di aggregazione, le tecniche di visualizzazione e
l'identificazione di relazioni funzionali tra le variabili
12
Principali Funzioni del Data Mining (3)
•
Dependency Modeling: consiste nella ricerca di un modello che descriva
dipendenze significative tra le variabili.
I modelli di dipendenza esistono a due livelli: il livello strutturale del
modello specifica, spesso in forma grafica, quali variabili sono localmente
dipendenti da altre, mentre il livello quantitativo del modello specifica la
forza della dipendenza usando una qualche scala numerica.
Per esempio, le reti di dipendenza probabilistica usano l'indipendenza
condizionale per specificare l'aspetto strutturale del modello e le
probabilità o la correlazione per specificare la forza della dipendenza
13
Clustering - Introduzione (1)
• Partizionare un grande insieme di oggetti in clusters omogenei è
un’operazione fondamentale in data mining
• L’algoritmo cosiddetto k-means è molto adatto per svolgere
quest’operazione poiché è efficiente
• L’unico problema è che è di limitata applicabilità, in quanto tratta
unicamente dati numerici
• Vedremo brevemente l’algoritmo k-means e una sua estensione per dati
categorici
14
Clustering - Introduzione (2)
• L’operazione di clustering è necessaria per diverse funzioni del data
mining tra cui la classificazione “unsupervised”, la segmentazione di grossi
data set eterogenei in più piccoli sotto-insiemi omogenei che possono
essere facilmente gestiti e analizzati separatamente
• I metodi di clustering dividono un insieme di oggetti in clusters tali che gli
oggetti nello stesso cluster sono più simili tra loro rispetto agli oggetti in
cluster diversi secondo qualche criterio predefinito
• I metodi statistici di clustering usano misure di similarità per partizionare gli
oggetti, mentre metodi di clustering concettuale partizionano gli oggetti
sulla base dei concetti associati agli oggetti
• La caratteristica del data mining è che tratta grosse quantità di dati
15
Clustering - Introduzione (3)
• La dimensione dei data set richiede che gli algoritmi usati siano scalabili
• Spesso gli algoritmi correntemente usati nel data mining non offrono
grande scalabilità in quanto sono stati originariamente sviluppati per
applicazioni diverse che coinvolgevano data set più piccoli
• Lo studio di algoritmi scalabili per il data mining è recentemente diventato
un importante argomento di ricerca
• Dopo una breve presentazione dell’algoritmo k-means, introdurremo la
sua variante k-modes per trattare dati categorici
• Confrontati con altri metodi di clustering, l’algoritmo k-means e le sue
varianti mostrano efficienza anche applicati a grossi data set
16
Introduzione (4)
• L’algoritmo k-means minimizza una funzione di costo calcolando i valori
medi dei cluster e pertanto il suo impiego è limitato a valori numerici
• Le applicazioni di data mining coinvolgono spesso dati categorici
• L’approccio tradizionale di conversione di dati categorici in dati numerici
non è sempre significativo (ad esempio quando i domini categorici non
sono ordinati)
• L’algoritmo k-modes elimina questo incoveniente ed estende il concetto
dei k-means anche a dati categorici, preservando l’efficienza dell’algoritmo
k-means
• Esiste una versione più complessa dell’algoritmo k-modes che si chiama
k-prototypes che tiene conto di attributi misti, categorici e non.
17
Introduzione (4)
• L’algoritmo k-prototypes definisce una misura di dissimilarità mista per
attributi categorici e numerici
• Sia sn la dissimilarità per attributi numerici basata sul quadrato della
distanza euclidea
• Sia sc la dissimilarità per attributi categorici definita come il numero di
categorie diverse tra due oggetti
• Definiamo la misura di dissimilarità tra due oggetti come sn+ysc dove y è
un peso per bilanciare le due parti ed evitare che un tipo di attributo sia più
considerato dell’altro
• Il processo di clustering dell’algoritmo k-prototypes è simile a k-means
• Un problema è la scelta opportuna del peso y
18
Introduzione (5)
• L’algoritmo k-modes è una semplificazione del metodo k-prototypes in
quanto tiene conto solo degli attributi categorici
• In questo caso non abbiamo più bisogno di definire un peso y
• Nel caso in cui comparissero attributi numerici nel problema occorrerebbe
renderli categorici
• Il maggior vantaggio del metodo consiste nella sua grande scalabilità e
pertanto nella possibilità di essere applicato a grandi data set
• Un altro approccio è stato presentato per applicare l’algoritmo k-means a
dati categorici previa conversione dei dati categorici in dati numerici
• In questo metodo molteplici attributi categorici vengono trasformati in
attributi binari (usando 0 o 1 per indicare se una categoria è assente o
presente)
19
Introduzione (5)
• Quindi gli attributi resi binari vengono considerati numerici e sottoposti
all’algoritmo k-means
• Se impiegato nel data mining, questo approccio richiede di gestire un
numero molto grande di attributi binari, in quanto i data set impiegati nel
data mining spesso hanno attributi categorici con centinaia o migliaia di
categorie.
• Questo aumenta inevitabilmente la complessità e il costo dell’algoritmo
• Inoltre i cluster means, dati da valori reali tra 0 e 1 non indicano le
caratteristiche del cluster
• Per contro l’algoritmo k-modes lavora direttamente su attributi categorici e
produce i cluster modes che descrivono i clusters e pertanto risutano utili
nell’interpretazione dei risultati
20
Domini e Attributi Categorici (1)
• Per dati categorici intendiamo dati che descrivono oggetti che hanno solo
attributi categorici
• Consideriamo che tutti gli attributi numerici siano inseriti in categorie
• Siano A1, A2,…,Am m attributi che descrivono uno spazio S e DOM(A1),
DOM(A2),…, DOM(Am) i domini degli attributi
• Un dominio DOM(Aj) è definito categorico se è finito e non ordinato, per
es., per ogni a,b∈ DOM(Aj) o a=b, o a≠b
• Aj è chiamato attributo categorico
• S è uno spazio categorico se tutti gli attributi A1, A2,…,Am che lo
descrivono sono categorici
• Un valore speciale, denotato con ε, è definito su tutti i domini categorici ed
è usato per rappresentare valori mancanti
21
Domini e Attributi Categorici (2)
• Per semplificare la misura di dissimilarità non consideriamo le relazioni di
inclusione concettuale tra valori in un dominio categorico (ad esempio il
fatto che automobile e veicolo sono due valori categorici in un dominio e
concettualmente un automobile è anche un veicolo)
22
Oggetti Categorici (1)
• Un oggetto categorico X∈S è logicamente rappresentato come una
congiunzione di coppie attributo-valore [A1=x1] ∧ [A2=x2] ∧ … ∧ [Am=xm]
dove xj ∈DOM(Aj) per 1 ≤ j ≤ m
• Senza ambiguità rappresentiamo X come un vettore [x1, x2,…,xm]
• Consideriamo che ogni oggetto in S abbia esattamente m attributi. Se il
valore di un attributo Aj non è disponibile per un oggetto X, allora Aj= ε
• Sia X = {X1, X2, ..., Xn} un insieme di n oggetti categorici e X⊆S
• L’oggetto Xi e’ rappresentato come [xi1, xi2,…,xim]
• Diciamo che Xi= Xk se xij= xkj per 1≤j ≤m
• La relazione Xi= Xk non significa che Xi e Xk sono lo stesso oggetto
23
Oggetti Categorici (2)
• Significa che i 2 oggetti hanno gli stessi valori categorici negli attributi A1,
... ,Am
• Ad esempio 2 pazienti in 1 ospedale possono avere gli stessi valori negli
attributi: Sesso, Malattia, Trattamento ma avere diverso Nome, Indirizzo,
Eta’... che sono attributi non selezionati per il clustering
• Supponiamo che X sia composto da n oggetti di cui p sono distinti
• Sia N la cardinalita’ del prodotto cartesiano DOM(A1) x DOM(A2) x
DOM(Am)
• Abbiamo p ≤N mentre n puo’ essere maggiore di N, nel caso che contenga
duplicati
24
Algoritmo k-means
• L’algoritmo k-means e’ costruito su 4 operazioni di base:
1) selezione dei k valori medi iniziali per i cluster
2) calcolo della dissimilarita’ tra un oggetto e la media di un cluster
3) allocazione di un oggetto nel cluster la cui media e’ piu’ vicina all’oggetto
4) Ri-calcolo della media del cluster dagli oggetti allocati in esso in modo
tale che la dissimilarita’ intra-cluster sia minimizzata
• Tranne che la prima operazione, le altre 3 vengono ripetute fino a
convergenza
25
Algoritmo k-means (2)
• L’essenza dell’algoritmo e’ la minimizzazione della funzione di costo:
k
n
E = ∑∑ yi ,l d ( X i ,Q l )
l =1 i =1
• dove n e’ il numero degli oggetti in un data set X, Xi∈X, Ql e’ la media del
cluster l, e yi,l e’ un elemento di una matrice di partizione Ynxk, d e’ una
misura di dissimilarita’ generalmente definita dal quadrato della distanza
euclidea
• Esistono diverse varianti dell’algoritmo che differiscono nella selezione
iniziale dei centri dei cluster, nel calcolo della dissimilarita’ e nelle strategie
per calcolare i centri dei cluster
26
Algoritmo k-means (3)
• L’algoritmo k-means ha le seguenti importanti proprieta’:
1. E’ efficiente nel gestire grosse quantita’ di dati. La complessita’
computazionale dell’algoritmo e’ O(tkmn) dove m e’ il numero di attributi, n
il numero di oggetti, k il numero dei cluster, e t e’ il numero di iterazioni
sull’intero data set. In genere, k,m,t << n .
2. Spesso l’algoritmo termina in un ottimo locale. Per trovare l’ottimo globale
possono essere adottate altre tecniche (deterministic annealing, algoritmi
genetici) da incorporare al k-means
3. Funziona solo su valori numerici in quanto minimizza una funzione di
costo calcolando la media dei clusters
4. I cluster hanno forma convessa. Pertanto e’ difficile usare il k-means per
trovare cluster di forma non convessa
27
Algoritmo k-means (5)
• Una difficolta’ consiste nel determinare il numero dei cluster
• Alcune varianti dell’algoritmo includono una procedura per cercare il k
ottimo
• L’algoritmo k-means e’ il migliore per il data mining per la sua efficienza
con i grossi data set
• Purtroppo, funzionando solo per valori numerici, limita di molto la sua
applicabilita’
• Discuteremo alcune modifiche all’algoritmo per renderlo adatto a valori
categorici
28
Algoritmo k-modes (1)
• L’algoritmo k-modes e’ una versione semplificata del k-prototypes
• In questo algoritmo abbiamo 3 differenze principali rispetto al k-means:
1. Usa una diversa misura di dissimilarita’
2. Sostituisce i k-means con i k-modes
3. Usa un metodo basato sulla frequenza per aggiornare i modes
29
Misure di dissimilarita’ (1)
• Siano X e Y due oggetti categorici descritti da m attributi categorici
• La misura di dissimilarita’ tra X e Y puo’ essere definita dal totale delle
differenze tra le corrispondenti categorie di attributi dei due oggetti
• Minore e’ il numero degli attributi diversi, piu’ i due oggetti sono simili
• Formalmente:
d ( X , Y ) = ∑ δ (x j , y j )
m
j =1
0
δ (x j , y j ) = 
1
(x
(x
j
j
(1)
= yj)
≠ yj)
30
Misure di dissimilarita’ (2)
• d(X,Y) da’ uguale importanza ad ogni categoria di un attributo
• Se teniamo in conto le frequenze delle categorie in un data set, possiamo
definire la misura di dissimilarita’ come:
m
d χ 2 ( X ,Y ) = ∑
j =1
(n
xj
+ ny j
nx j n y j
)δ (x , y )
j
j
(2)
• dove nx e ny sono il numero di oggetti nel data set che hanno le
j
j
categorie xj e yj per l’attributo j.
•
d χ 2 ( X , Y ) si dice distanza chi-quadro
31
Misure di dissimilarita’ (3)
• Questa seconda misura di dissimilarita’ da’ piu’ importanza alle categorie
rare piuttosto che a quelle frequenti
• Per questo viene usata per scoprire cluster di oggetti sotto-rappresentati
come ad es. i richiami fraudolenti nei database delle assicurazioni
32
“Mode” di un set
• Sia X un insieme di oggetti categorici descritti dagli attributi categorici A1,
A2, ... , Am
• Un “mode” di X e’ un vettore Q=[q1, q2, ... , qm]∈S che minimizza:
n
D (Q , X ) = ∑ d ( X i , Q )
i =1
• dove X={X1, X2, ..., Xn} e d possono essere definiti come nell’eq. (1) o
nell’eq. (2).
• Q non e’ necessariamente un elemento di X
33
Ricerca di un “Mode” per un set
• Sia
nck , jil numero di oggetti aventi la categoria
fr ( Aj = ck , j | X ) =
• la frequenza relativa della categoria
ck , j nell’attributo Aj e
nc k , j
n
ck , j
in X
• Teorema: la funzione D(Q,X) e’ minimizzata se e solo se:
f r (Aj = q j | X ) ≥ f r (Aj = ckj | X )
per q j ≠ ck , j per ogni j = 1,..., m
34
L’algoritmo k-modes (1)
• Sia {S1, S2, ..., Sk} una partizione di X, dove Sl ≠ Ø per 1 ≤ l ≤k e {Q1, ...,
Qk} i modi di {S1, ..., Sk}
• Il costo totale della partizione e’ definito da:
k
n
E = ∑∑ yi ,l d ( X i , Ql )
l =1 i =1
• dove yi,l e’ un elemento di una matrice di partizione Ynx1 e d puo’ essere
definito come in 1 o come in 2
• Similmente all’algoritmo k-means, l’obiettivo del clustering di X e’ trovare
un set {Q1, Q2, ..., Qk} che minimizzi E.
35
L’algoritmo k-modes (2)
• L’algoritmo k-modes consiste nei passi seguenti :
1. Scegliere k modi iniziali, uno per ogni cluster
2. Allocare un oggetto in un cluster il cui modo sia il piu’ vicino ad esso,
secondo la definizione di d. Aggiornare il modo del cluster dopo ogni
allocazione secondo il teorema
3. Dopo che tutti gli oggetti sono stati allocati nei cluster, ripetere il test della
dissimilarita’ degli oggetti in relazione ai modi correnti. Se si trova che un
oggetto e’ piu’ vicino al modo di un altro cluster piuttosto che al proprio
corrente, riallocare l’oggetto in quel cluster e aggiornare i modi di entrambi
4. Ripetere il passo 3 finche’ nessun oggetto cambia cluster dopo un ciclo
completo di test sull’intero data set
36
L’algoritmo k-modes (3)
• Come l’algoritmo k-means, l’algoritmo k-modes produce soluzioni
localmente ottime che sono dipendenti dai modi iniziali e dall’ordine degli
oggetti nel data set
• L’impiego di opportuni metodi di scelta dei modi iniziali, puo’ migliorare il
risultato del clustering
• Vediamo un metodo di selezione dei k modi iniziali. Il metodo si sviluppa
nei seguenti passi:
1. Calcolare le frequenze di tutte le categorie per tutti gli attributi e
immagazzinarli in un array di categorie in ordine discendente di frequenza
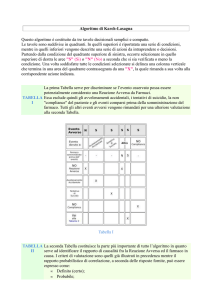
come in Fig.1. Qui ci,j denota la categoria i dell’attributo j e f(ci,j)≥ f(ci+1,j)
dove f(ci,j) e’ la frequenza della categoria ci,j
37
L’algoritmo k-modes (4)
Fig.1
 c1,1 c1, 2
c
 2,1 c2, 2

c3,1
c4,1
c1,3
c2,3
c3,3
c4,3
c1, 4 
c2, 4 

c3, 4 

• La figura mostra l’array di categorie per un data set con 4 attributi aventi
rispettivamente 4, 2, 4, 3 categorie
2. Assegnare le categorie piu’ frequenti uniformemente ai k modi iniziali.
Per l’esempio in Fig.1 assumiamo k=3.
Assegnamo Q1=[q1,1=c1,1, q1,2=c2,2, q1,3=c3,3, q1,4=c1,4], Q2=[q2,1 =c2,1, q2,2
=c1,2, q2,3 =c4,3, q2,4 =c2,4], Q3=[q3,1 =c3,1, q3,2 =c2,2, q3,3 =c1,3, q3,4 =c3,4]
38
L’algoritmo k-modes (4)
3. Incominciamo con Q1. Scegliamo il record piu’ simile a Q1 e sostituiamo
Q1 con il record come primo modo iniziale. Poi scegliamo il record piu’
simile a Q2 e sostituiamo Q2 con il record come secondo modo iniziale.
Continuiamo questo processo fino alla sostituzione di Qk
In queste selezioni Ql≠Qt per l ≠t
Il passo 3 serve per evitare il caso di cluster vuoti.
L’obiettivo di questo metodo di selezione e’ di rendere distanti i modi iniziali
il che puo’ risultare in un miglior clustering.
39
Classificazione e Regressione - Introduzione (1)
• Classificazione e regressione sono problemi a cui comunemente viene
applicato il data mining
• Tipicamente classificazione e regressione vengono usate come supporto
decisionale nel marketing e nel CRM (previsione dei comportamenti di
acquisto, identificazione dei target per promozioni, nuovi prodotti...) ma
anche per l’identificazione di frodi, nella credit risk detection, in problemi
di diagnostica medica...
• Esistono diverse tecniche di data mining per affrontare problemi di
classificazione e di regressione e generalmente ogni tecnica dispone di
diversi algoritmi. Naturalmente queste tecniche producono modelli diversi
ma in generale ogni tecnica genera un modello predittivo basato su dati
storici che viene poi impiegato per predire l’uscita di nuovi casi.
• Cio’ che distingue classificazione e regressione e’ il tipo di output che
viene predetto
40
Classificazione e Regressione - Introduzione (2)
• La classificazione individua l’appartenenza ad una classe. Per esempio un
modello potrebbe predire che il potenziale cliente ‘X’ rispondera’ ad
un’offerta. Con la classificazione l’output predetto (la classe) e’ categorico
ossia puo’ assumere solo pochi possibili valori come Si’, No, Alto, Medio,
Basso...
• La regressione predice un valore numerico specifico. Ad esempio un
modello potrebbe predire che il cliente X ci portera’ un profitto di Y lire nel
corso di un determinato periodo di tempo. Le variabili in uscita possono
assumere un numero illimitato (o comunque una grande quantita’) di
valori. Spesso queste variabili in uscita sono indicate come continue
anche se talvolta non lo sono nel senso matematico del termine (ad
esempio l’eta’ di una persona)
41
Classificazione e Regressione - Introduzione (3)
• Classificazione e regressione sono comunque strettamente correlate e
spesso risulta semplice trasformare un problema di classificazione in una
regressione e viceversa
• In generale un problema di regressione viene trasformato in un problema
di classificazione semplicemente raggruppando i valori continui predetti in
categorie discrete, mentre un problema di classificazione viene
trasformato in una regressione identificando un punteggio o probabilita’
per ogni categoria ed assegnando un range di punteggi ad ogni categoria
• Nonostante esista la possibilita’ di convertire classificazione in regressione
e viceversa e’ importante osservare che, a livello di strumenti, i risultati piu’
accurati si ottengono con il matching di tool e task
42
Tecniche di predictive modeling (1)
• Esistono 4 tecniche che attualmente dominano il mercato degli strumenti
per classificazione e regressione:
1) Decision Tree: e’ una tecnica che genera una rappresentazione
grafica ad albero del modello che produce. Generalmente e’
accompagnata da regole della forma “IF condition THEN outcome”
che costutuiscono la versione testuale del modello. Gli algoritmi di
Decision Tree comunemente implementati comprendono Chisquared Automatic Interaction Detection (CHAID), Classification and
Regression Trees (CART), C4.5 e C5.0. Tutti questi sono
estremamente adatti alla classificazione, alcuni sono impiegabili
anche per la regressione.
43
Tecniche di predictive modeling (2)
2) Neural networks: sono tra i piu’ complicati algoritmi di
classificazione e regressione. Vengono usate comunemente
nell’identificazione di frodi dove occorre un algoritmo che rilevi
accuratamente ogni eccezione e che funzioni in tempo reale.
Infatti, sebbene la fase di training di una rete neurale possa essere
time consuming, una rete allenata puo’ effettuare previsioni su nuovi
casi molto rapidamente.
L’output di una rete neurale e’ puramente predittivo e spesso difficile
da comprendere e da impiegare. Queste difficolta’ spesso
scoraggiano l’uso di reti neurali nel supporto decisionale.
44
Tecniche di predictive modeling (3)
3) Naive-Bayes: e’ una tecnica di classificazione sia predittiva che
descrittiva. Analizza la relazione tra ogni variabile indipendente e la
variabile dipendente per derivare una probabilita’ condizionata per
ogni relazione.
Quando si analizza un nuovo caso, viene fatta una previsione
combinando gli effetti delle variabili indipendenti sulle variabili
dipendenti (l’uscita che viene predetta).
Per esempio consideriamo il problema di cercare di predire il
turnover dei clienti dove è noto che il 75% dei clienti con
fatturazioni mensili tra $400 e $500 ha abbandonato e il 68% dei
clienti che ha fatto più di 4 chiamate al customer service ha
abbandonato. Applicando la tecnica a un cliente con fatturazione
mensile di $480 e che ha fatto 5 chiamate al customer service,
Naive Bayes predice che il cliente ha una alta probabilità di
abbandono.
45
Tecniche di predictive modeling (3)
In teoria i risultati sarebbero corretti solo se le variabili indipendenti
fossero statisticamente indipendenti l’una dall’altra. Questo spesso
non e’ vero ma la pratica dimostra che Naive Bayes fornisce buoni
risultati e la sua semplicita’ e velocita’ ne fanno uno strumento
ideale per modellare ed investigare relazioni semplici
46
Tecniche di predictive modeling (4)
4) K-nearest neighbor (K-NN): differisce dalle precedenti tecniche nel
fatto che i dati di training non sono usati per creare il modello ma
costituiscono essi stessi il modello. Quando si presenta un nuovo
caso, l’algoritmo scandisce tutti i dati per trovare un sottoinsieme di
casi che sono piu’ vicini ad esso e li usa per predire l’uscita.
Ci sono due aspetti principali nell’algoritmo k-NN: il numero di casi
piu’ vicini da usare (k) e la scelta di una metrica per misurare cosa si
intende per ‘piu’ vicini’.
Per classificare un nuovo caso, l’algoritmo calcola la distanza dal
nuovo caso ad ogni caso nel training data. L’uscita prevista per il
nuovo caso corrisponde all’uscita predominante nei k casi piu’ vicini
del training set.
47
Tecniche di predictive modeling (5)
Tutte le tecniche menzionate possono generare modelli predittivi.
Alcune di esse forniscono anche modelli descrittivi che consentono di
comprendere piu’ a fondo le relazioni tra i dati, indipendentemente dalla
natura predittiva del modello.
Ad esempio questa informazione potrebbe essere nella forma: “il guadagno
e’ il fattore piu’ importante per determinare se qualcuno e’ a un buon livello
di credit risk”.
Tale informazione descrittiva puo’ essere presentata in forma testuale o
attraverso tool di visualizzazione.
48
Esempi di classificazione lineare e non lineare
Debito
Debito
“Prestito NON concesso”
zona di
“Prestito NON concesso”
zona di
“Prestito concesso”
CLASSIFICAZIONE LINEARE
“Prestito concesso”
Introito
NEAREST NEIGHBOR
Debito
x
“Prestito NON concesso”
x
x
x
“Prestito concesso”
RETI NEURALI
Introito
Introito
49
Decision Tree
• I dati in input rappresentano il training set e sono costituiti da molteplici
esempi (records), ognuno caratterizzato da diversi attributi (features)
• Ogni esempio e’ caratterizzato dall’appartenenza ad una classe (class
label)
• Obiettivo della classificazione e’ di analizzare i dati in input e sviluppare un
accurato modello per ogni classe tramite il quale sia possibile classificare i
futuri dati di test per cui i class label sono ignoti
• I decision tree sono relativamente veloci, confrontati con altri metodi di
classificazione e sono di semplice interpretazione: essi possono facilmente
essere convertiti in insiemi di regole di classificazione e in query SQL per
accedere ai database
50
Esempio
ETA’
SALARIO
30
65
B
23
15
C
40
75
B
CLASSE
ETA’<=35
SALARIO’<=40
C
SALARIO’<=50
B
C
B
55
40
C
55
100
B
Decision rule per la prima foglia a sin:
45
60
B
IF eta’<=35 AND salario<=40 THEN classe=C
51
Decision Tree Classification
• La maggior parte dei classificatori ad albero (es. CART, C 4.5) realizzano
la classificazione in 2 fasi: Tree Building e Tree Pruning
Tree Building: in questa fase si costruisce un primo decision tree
partizionando ripetutamente i dati del training set. Il training set e’ suddiviso
in due o piu’ partizioni usando un attributo (esistono algoritmi che usano
anche attributi multipli). Questo processo viene ripetuto ricorsivamente
finche’ tutti gli esempi in una partizione appartengono ad una classe.
Tree Pruning: l’albero costruito nella prima fase classifica completamente il
training data set. Questo implica che vengono creati rami anche per il
rumore e le fluttuazioni statistiche. Questi rami possono condurre a errori
nella classificazione dei dati di test. La fase di pruning ha l’obiettivo di
rimuovere questi rami dal decision tree selezionando il sotto-albero con il
minimo tasso di errore stimato
52
Tree Building Algorithm
MakeTree (Training Data T)
Partition (T);
Partition (Data S)
if (all points in S are in the same class) then return;
Evaluate splits for each attribute A
Use best split found to partition S into S1 and S2;
Partition (S1);
Partition (S2);
53
Tree Building
Durante il Tree Buiding vengono svolte due operazioni principali:
• Valutazione delle possibili suddivisioni dell’insieme per ogni attributo e
scelta della migliore
• Creazione delle partizioni usando la suddivisione migliore. Avendo
determinato la suddivisione migliore, le partizioni possono essere create
semplicemente applicando il criterio di suddivisione ai dati
La complessita’ risiede nella determinazione della suddivisione migliore
per ogni attributo. La scelta del criterio di splitting dipende dal dominio
dell’attributo che puo’ essere numerico o categorico (attributi con un
numero finito di possibili valori)
54
Splitting Index
Un indice di splitting viene usato per valutare la bonta’ delle alternative
possibili di suddivisione per un attributo.
Esistono diverse possibilita’ per l’indice di splitting. Frequentemente si usa il
gini index. Se un data set T contiene esempi da n classi, gini(T) e’ definito
come:
n
gini (T ) = 1 − ∑ p 2j
1
dove pj e’ la frequenza relativa della classe j in T
55
Split per attributi numerici
Per attributi numerici si usa uno split binario della forma A<=v dove v e’ un
numero reale. Il primo passo per valutare le suddivisioni per attributi
numerici consiste nell’ordinare i training examples sulla base del valore
dell’attributo considerato per lo splitting.
Siano v1, v2, ..., vn i valori ordinati di un attributo numerico A. Dal momento
che ogni valore tra vi e vi+1 suddivide l’insieme negli stessi due sotto
insiemi, abbiamo da esaminare solo n-1 possibili splits. Tipicamente si
considera il punto medio di ogni intervallo vi - vi+1 come split point.
Il costo della valutazione delle suddivisioni per attributi numerici e’ dominato
dal costo di ordinamento dei valori.
56
Split per attributi categorici
Se S(A) e’ l’insieme dei possibili valori di un attributo categorico A, allora lo
A∈ S '
split test e’ della forma dove
S'⊂ S
Dal momento che il numero di possibili sottoinsiemi per un attributo con n
possibili valori e’ 2n, la ricerca del miglior sottoinsieme puo’ essere onerosa.
57
Tree Pruning (1)
La fase di tree pruning esamina l’albero costruito tramite il training set e
sceglie il sotto-albero con il minimo errore stimato.
Esistono due approcci principali alla stima del tasso di errore: uno impiega
il training data set originale e l’altro usa un dataset indipendente per la
stima dell’errore
La Cross-Validation appartiene alla prima categoria. Diversi campioni sono
estratti dai dati di training e per ogni campione si genera un albero. Questi
alberi multipli sono poi usati per stimare il tasso di errore dei sotto-alberi
dell’albero originale
58
Tree Pruning (2)
La seconda classe di metodi divide i dati di training in due parti dove una
parte viene usata per costruire l’albero e l’altra per fare il pruning.
I problemi di questo metodo riguardano la scelta dei dati di test e la
dimensione dell’insieme di test che va a scapito della dimensione del
training set
59
Principali Funzioni del Data Mining (4)
•
Change and Deviation Detection: le tecniche di change and deviation
detection hanno come obiettivo la scoperta dei cambiamenti più
significativi nei dati rispetto a valori di norma o recentemente misurati .
La ricerca di pattern in serie temporali di dati è l’esempio più frequente di
questo tipo di funzione di data mining