Lezione 11
Onde e fenomeni ondulatori
Fenomeni in cui vi è trasmissione di movimento,
di energia (e di quantità di moto) senza scambio
di materia (che rimane sempre intorno alla sua
posizione media, o di equilibrio)
v
Le onde sono spesso prodotte da oscillazioni
(anche non regolari) di oggetti o circuiti
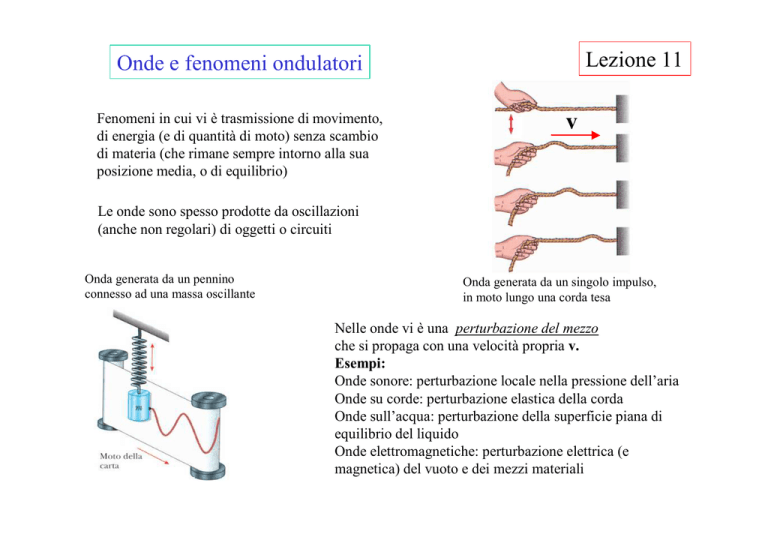
Onda generata da un pennino
connesso ad una massa oscillante
Onda generata da un singolo impulso,
in moto lungo una corda tesa
Nelle onde vi è una perturbazione del mezzo
che si propaga con una velocità propria v.
Esempi:
Onde sonore: perturbazione locale nella pressione dell’aria
Onde su corde: perturbazione elastica della corda
Onde sull’acqua: perturbazione della superficie piana di
equilibrio del liquido
Onde elettromagnetiche: perturbazione elettrica (e
magnetica) del vuoto e dei mezzi materiali
Tipi fondamentali di onde
v
Onde trasversali: l’oscillazione (o la perturbazione) è in
direzione perpendicolare alla direzione di propagazione
dell’onda (il movimento del punto P è verticale mentre l’onda
viaggia in orizzontale)
Onde longitudinali: l’oscillazione (o la perturbazione) è
nella stessa direzione della direzione di propagazione
dell’onda (il movimento è orizzontale come la velocità;
ad esempio le onde sonore sono longitudinali)
v
Onde miste: combinazione di moti
trasversali e longitudinali.
Nelle onde sulla superficie dell’acqua
le particelle hanno un movimento
quasi circolare.
v
Descrizione matematica di un’onda (in una dimensione)
yM
y
v
0 x0
x
A un certo istante l’onda è descritta da
una funzione y = f(x); un certo punto
dell’onda (ad esempio l’ampiezza
massima yM) ha coordinata x0
y
yM
v⋅t
0 x0
x1
Esempio con un profilo di
onda trasversale
Asse y: direzione dello
spostamento del punto
Asse x positivo:
direzione di propagazione
v
x
Dopo un tempo t l’onda si è spostata
di v·t, e l’ampiezza massima si trova
sul punto x1 = x0 + vt; quindi si ha:
La funzione che descrive in generale l’onda
propagante in direzione +x è quindi →
yM = f ( x0 ) = f ( x1 − vt )
Se l’onda si propaga in
direzione x negativa si ha
y = f ( x − vt )
y = f ( x + vt )
(è una funzione di due variabili, lo spazio x e il tempo t)
Velocità di un’onda su una corda tesa
v=
F
µ
F : tensione della corda (in Newton)
µ : massa della corda per unità di
lunghezza (in Kg/m) (µ = ∆m/∆x)
F
v
∆m
F
∆x
(generate da moti oscillatori armonici)
Onde sinusoidali
Forma generale con costante k (detta numero d’onda)
y = A ⋅ sin[k ( x − vt )]
([k ] = rad/m)
y
A è l’ampiezza massima dell’onda
v è la velocità di propagazione dell’onda
Introducendo la pulsazione
si ha la forma più usata
ω = v k ([ω ] = rad/s)
A
y = A ⋅ sin (kx − ωt )
(kx − ω t ) è la fase dell’onda
(= angolo argomento della funzione seno)
(
Più in generale: y = A ⋅ sin kx − ωt + ϕ
dove si inserisce la costante di fase ϕ che
specifica le condizioni iniziali dell’onda
)
Periodicità spaziale: la distanza ∆x tra due
punti equivalenti dell’onda si definisce
lunghezza d’onda λ e deve corrispondere a
una variazione di fase di un angolo giro (a t
fissato), quindi →
x
grafico a t fissato: si osserva
la periodicità spaziale
(fotografia)
y = A ⋅ sin (kx + ϕ )
k ⋅ ∆x = k ⋅ λ = 2π
λ=
2π
k
Periodicità temporale: la distanza ∆t tra due punti
equivalenti dell’onda è il periodo T e deve corrispondere a
una variazione di fase di un angolo giro (a x fissato),
quindi:
ω ⋅ ∆t = ω ⋅ T = 2π
T = 2π / ω
Infine da ω = v k
Frequenza dell’oscillazione:
ν=
y
A
t
1 ω
=
T 2π
2πν = v ⋅ 2π / λ si trova
v = λ ⋅ν
relazione fondamentale che lega la velocità di propagazione
con la lunghezza d’onda e la frequenza
Energia trasportata da un’onda
grafico a x fissato si osserva
la periodicità temporale
(oscillatore armonico)
y = A ⋅ sin (ωt + ϕ )
1
Per un’oscillatore
E0 = kosc A2 ; kosc = m ⋅ ω 2
armonico:
2
Consideriamo un’onda sinusoidale su un tratto di corda di massa
2
2
∆m ; ogni elemento della corda esegue un moto armonico, e
∆E 1 2 ∆m ω A
1
2
2
=
=
µ
ω
A
l’energia per unità di lunghezza che viaggia sulla corda sarà
∆x
2
∆x
proporzionale ai quadrati della pulsazione e dell’ampiezza.
Nell’intervallo di tempo ∆t questa energia
1 ∆m ω 2 A2 1 µ ∆x ω 2 A2
viene trasferita al tratto di corda successivo;
∆E
1
= 2
= 2
= µ v ω 2 A2
P=
la potenza (energia per unità di tempo)
∆t
∆t
∆t
2
trasportata dall’onda è anche
proporzionale alla velocità di propagazione.
Sovrapposizione e interferenza
Principio di sovrapposizione: se due (o più) onde si muovono in un mezzo, la funzione
dell’onda risultante è in ogni punto la somma algebrica delle funzioni fi(x,t) delle singole onde
La combinazione di onde nella
stessa regione di spazio è detta
interferenza
yT = y1 + y2
Esempio di interferenza costruttiva
Due onde che si propagano in
direzioni opposte possono
attraversarsi senza venire
modificate.
Due onde con ampiezze di verso
opposto si sovrappongono dando
interferenza distruttiva; se le
ampiezze sono uguali si ha
completa scomparsa dell’onda
risultante all’istante della
sovrapposizione (interferenza
completamente distruttiva)
Sovrapposizione e interferenza di onde sinusoidali
Due onde sinusoidali uguali (A,k,ω uguali), e nella stessa
direzione, ma con una differenza di fase pari a ϕ (ad
esempio possono essere generate dalla stessa sorgente ma
seguire percorsi diversi prima di sovrapporsi)
y2 = A ⋅ sin (kx − ωt + ϕ )
y1 = A ⋅ sin (kx − ωt ) ;
La loro sovrapposizione (con le regole trigonometriche)
Ampiezza dell’onda
risultante
y = y1 + y2 = 2 A ⋅ cos(ϕ / 2) ⋅ sin (kx − ωt + ϕ / 2 )
Onda sinusoidale con la
medesima lunghezza
d’onda e frequenza
Differenza di fase ϕ = 0
interferenza costruttiva
(massima ampiezza = 2A)
Differenza di fase ϕ = π
interferenza completamente
distruttiva (ampiezza = 0)
Esempio di onda stazionaria
su una corda tesa
Onde stazionarie
Su una corda bloccata alle due estremità, le onde che si propagano subiscono
riflessione agli estremi. La sovrapposizione delle onde con le loro riflesse
forma onde stazionarie, in cui periodicità spaziale e temporale sono separate:
onda propagante verso -x ;
onda propagante verso +x
x
y1 = A ⋅ sin(kx + ωt + ϕ1 )
y2 = A ⋅ sin (kx − ωt + ϕ 2 )
y = y1 + y2 = 2 A ⋅ sin(kx + (ϕ1 + ϕ 2 ) / 2 ) ⋅ cos(ωt + (ϕ1 − ϕ 2 ) / 2)
Forma dell’onda:
→ sin (kx + ϕ 0 )
Ampiezza dell’oscillazione,
funzione della posizione
Oscillazione armonica
nodi: punti in cui
(trasversale) degli elementi
l’ampiezza è nulla
della corda intorno alla
ventri: punti in cui
posizione di equilibrio
l’ampiezza è massima
Posizione dei nodi: in x = 0 e in x = L deve essere ampiezza zero, quindi
ricaviamo la lunghezza d’onda e frequenza propria dell’ onda stazionaria:
λ
= nπ
λ=
2L
n
kL = nπ
ϕ0 = 0
2π
0 = sin( kL + 0)
x=L
0 = sin(0 + ϕ 0 )
x=0
v=n
(con n intero qualsiasi)
v
2L
L=n
λ
2
La lunghezza della corda
corrisponde a un numero intero
di mezze lunghezze d’onda
Effetto Doppler
Moto relativo tra sorgente e osservatore: viene percepita una
frequenza di oscillazione dell’onda diversa da quella a riposo
(fenomeno ben noto per le onde sonore)
λ
=ν +
O
v /ν
=ν 1+
O
v
>ν
λD = λ −
vS
ν
=λ−
Sorgente in moto con velocità vS verso l’osservatore : in
un periodo di oscillazione T , i fronti d’onda vengono
“schiacciati” perchè la cresta successiva guadagna lo
spazio vS · T = vS / ν. La lunghezza d’onda percepita
dall’osservatore è quindi diminuita di:
Sorgente che emette un’onda sonora di velocità
v che si propaga nello spazio come onda sferica;
le linee sono le creste dell’onda
O
νD =ν +
Osservatore fermo: frequenza percepita = numero di
vibrazioni per unità di tempo → ν = v / λ
Osservatore in moto verso la sorgente con velocità vO : nell’unità di tempo,
oltre alle vibrazioni precedenti vengono percepite anche le vibrazioni ricevute
avanzando di vO (·1s) e cioè vO / λ nuove vibrazioni. La frequenza percepita
sarà aumentata:
v
v
v
vS
v
= λ 1− S
v /λ
v
νD =
v
λD
=
λD
La frequenza percepita sarà quindi aumentata di:
v
v
=ν
>ν
(
)
v − vS
λ 1 − vS /v
N.B. nei casi opposti in cui vi sia allontanamento,
basta cambiare il segno a vO o a vS
ω=
Circuito LC – oscillazioni elettromagnetiche
Il circuito si comporta come un oscillatore armonico di frequenza ω: l’energia oscilla
continuamente tra il condensatore e l’induttanza. Idealmente l’energia si conserva,
ma le leggi del circuito non tiene conto della emissione e perdita di energia per
irraggiamento. Infatti deboli oscillazioni dello stesso tipo vengono osservate in un
circuito LC uguale e prossimo a quello eccitato (principio della radio).
rivediamo le leggi fondamentali dell’elettromagnetismo
Sup. chiusa
⇔
Teorema della
divergenza
Legge di Gauss per E e B in forma
differenziale o puntuale
(operatore divergenza)
div E =
ρ
ε0
div B = 0
div ... =
∂
∂
∂
+
+
∂x ∂y ∂z
ε0
∫ B ⋅ n dS = 0
Sup. chiusa
ΦB =
Qcont
∫ E ⋅ n dS =
Prime due leggi
(I e II eq. di Maxwell)
Legge di Gauss per E e B in
forma integrale
(flusso su superficie chiusa)
Nuovi fenomeni
V (t )
ΦE =
1
LC
Le leggi in forma differenziale sono in generale più utili. Esse sono infatti delle equazioni differenziali
(a derivate parziali) che ci dicono come i campi E e B variano punto per punto nello spazio (e nel
tempo ….) e richiedono solo la conoscenza di quantità o funzioni nel punto in esame (o in punti vicini)
Le altre due leggi
∫ B ⋅ ds = µ
C
d ΦB
dt
Legge di Ampere in forma integrale
∫ E ⋅ ds = = −
Legge di Faraday in forma integrale
0
I conc
C
Entrambe le leggi riguardano l’integrale dei campi sullo spostamento (“lavoro”) su un circuito chiuso C
Traduzione in forma differenziale: per mezzo del Teorema di Stokes:
il “lavoro” di un vettore lungo una linea chiusa è uguale al flusso, attraverso una superficie concatenata
con la linea, di una quantità vettoriale detta rotore o vorticità del campo vettoriale in esame. Con una
dimostrazione simile a quella fatta applicando il Teorema della divergenza alle prime due leggi si ha:
Vettore densità di corrente
(corrente per unità di superficie,
o densità di carica per velocità)
J (r ) = ρ v
rot è il rotore , un operatore differenziale vettoriale, scritto
esplicitamente come matrice di derivate parziali sulle variabili
spaziali x,y,z, e costruito rispettando la regola della mano destra.
Esso descrive le proprietà di vorticità, cioè se il campo vettoriale ha
linee di forza chiuse su se stesse (pensiamo ai vortici nei fluidi)
rot × B = µ 0 J
Significato: una opportuna combinazione di
derivate spaziali dei campi E e B è uguale a:
la variazione nel tempo del vettore B (per E),
proporz. al vettore densità di corrente J (per B)
∂B
∂t
rot × E = −
Legge di Ampere in forma differenziale
(?)
Legge di Faraday in forma differenziale
(III eq. di Maxwell)
Simmetria tra le leggi dell’ Elettromagnetismo (di Maxwell)
rot × B = µ 0 J
(?)
Alta simmetria
div B = 0
densità di carica elettrica ρ ⇔ densità
di carica magnetica (sempre = 0)
Bassa simmetria
(III)
rot × E = −
(II)
∂B
∂t
(I)
ρ
div E =
ε0
variazione nel tempo di un campo di forze ? ⇔
? densità di corrente (un oggetto materiale)
La mancanza di simmetria deriva dalla legge di Ampere,
che vale solo per correnti continue nello spazio
Flusso del
campo E(t)
I
∫ B ⋅ ds = µ
Esempio: campo magnetico creato da
una corrente entrante in un condensatore
circuito C
0
I conc
C
Iconc è la corrente che attraversa una qualsiasi superficie che ha per
bordo C; se la superficie è S1 la corrente concatenata è I mentre se
la superficie è la S2 (che avvolge il piatto terminale) la corrente
concatenata è zero! → la legge è contraddittoria se la corrente ha
delle discontinuità (come sorgenti o pozzi)
Ma attraverso la superficie S2 passa il flusso delle linee di forza
del campo elettrico del condensatore, che è crescente nel tempo!
d ΦE
IS = ε0
dt
Idea di Maxwell: completare la legge di Ampere (integrale)
aggiungendo la “corrente di spostamento”, proporzionale alla
variazione nel tempo del flusso del campo elettrico
d ΦE
dt
In tal modo entra nella legge di Ampere (differenziale) la
variazione nel tempo di un campo, come per la III legge.
Si ha una alta simmetria tra la III e la IV legge di Maxwell.
III (Faraday) : rot × E = −
∂B
∂t
d ΦE
C 2 N / C ⋅ m2 C
[I S ] = ε 0
=
⋅
= =A
dt
Nm 2
s
s
Osserviamo che la “corrente di spostamento” IS
ha proprio le dimensioni di una corrente
∂E
rot × B = µ0 J + µ0ε 0
∂t
= µ0 Iconc + µ0ε 0
(Teorema di
Stokes)
C
⇔
+ IS )
conc
0
∫ B ⋅ ds = µ (I
Legge di Ampere – Maxwell
in forma differenziale
(IV eq. di Maxwell)
Legge di Ampere – Maxwell
in forma integrale
Novità della IV legge di Maxwell:
i campi magnetici possono essere generati non solo da correnti,
ma anche da campi elettrici variabili nel tempo
ρ = 0; J = 0 )
∂B
∂t
(in assenza di cariche e correnti
Equazioni di Maxwell nel vuoto
rot × E = −
div B = 0
rot × B = µ0ε 0
assenza di
sorgenti
div E = 0
∂E
∂t
Si ha altissima simmetria
tra le equazioni per i campi
elettrico e magnetico
la variazione nel tempo del campo B genera il campo E
la variazione nel tempo del campo E genera il campo B
Campi elettrici e magnetici variabili nel tempo possono autosostenersi anche nel vuoto!
Queste eq. descrivono l’evoluzione, nello spazio e nel tempo, dei
campi vettoriali E e B intercorrelati. Sono eq. a derivate parziali sulle
coordinate x,y,z e t, e ammettono soluzioni di tipo ondulatorio. Ad
esempio, se consideriamo la componente di un campo elettrico in
direzione y che dipenda solo dalla coordinata spaziale x (cioè è
variabile, o in movimento, lungo l’asse x) dalle ultime 2 equazioni si
ricava una forma di equazione delle onde, cioè una equazione
differenziale a derivate parziali seconde il campo Ey (e altre eq. simili
per le altre componenti di E e B)
∂2E
∂2E
− µ 0ε 0 2 = 0
2
∂x
∂t
Equazione delle onde per
la funzione E(x,t), una
componente del campo E
Equazione delle onde
elettromagnetiche
⇒
soluzione di tipo ondulatorio,
ad esempio onda propagante in direzione +x
E ( x, t ) = E0 ⋅ sin(kx − ω t )
Verifica: calcolo delle derivate seconde:
∂2 E
∂ ∂
∂
=
E0 sin(kx − ωt ) =
(kE0 cos(kx − ωt )) = −k 2 E0 sin(kx − ωt )
2
∂x
∂x ∂x
∂x
µ 0ε 0ω 2 = k 2
deve essere quindi:
1
v2
Tm
µ 0 = 4π ⋅ 10
A
2
-12 C
ε 0 = 8.85 ⋅10
Nm 2
ampiezza
k
numero d' onda
ω pulsazione
2π
λ=
k
lunghezza d' onda
2π
ν=
ω
frequenza
c=
1
µ 0ε 0
= 2.99792 ⋅10 8 m/s
v = λ ⋅ν
velocità
(kx- x) fase
µ 0ε 0
−7
µ 0ε 0 =
La velocità delle onde elettromagnetiche nel
vuoto (da ora in poi indicata con c) è fissata
dalle costanti elettrica e magnetica, e vale:
1
v=
∂
∂2E ∂ ∂
E0 sin(kx − ωt ) = (− ωE0 cos(kx − ωt ) ) = −ω 2 E0 sin(kx − ωt )
=
2
∂t ∂t
∂t
∂t
∂2E
∂2E
− µ 0ε 0 2 = 0
− k 2 E0 sin( kx − ωt ) + µ 0ε 0ω 2 E 0 sin( kx − ω t ) = 0
2
∂x
∂t
E0
esattamente la velocità della luce!
Onde elettromagnetiche
La luce è un’onda elettromagnetica!
Caratteristiche delle onde e.m.
ω
Velocità di propagazione c =
2)
Nel vuoto, E e B sono tra loro perpendicolari,
e perpendicolari alla direzione di propagazione
(regola della mano destra E → B → c )
quindi le onde e.m. sono onde trasversali
3)
Vale la relazione tra i campi
4)
Polarizzazione: l’onda è polarizzata linearmente
se il campo E mantiene sempre la stessa direzione
nello spazio. Sono possibili anche polarizzazioni
circolari o ellittiche (quando la direzione di E
varia in modo regolare) o onde non polarizzate
(quando la direzione di E varia in modo casuale)
k
=
1
1)
µ 0ε 0
≈ 3 ⋅ 10 8 m/s
E
=c
B
Onda piana : un’onda che viaggia in una direzione
definita, e i cui campi E e B sono funzioni del tempo
e della sola variabile spaziale in quella direzione
Sono soluzioni delle eq. di Maxwell (nel vuoto),
per il campo elettrico E e per il campo magnetico
B accoppiati; un tipo fondamentale è l’onda
piana sinusoidale. Qualunque onda può essere
costruita sovrapponendo onde sinusoidali.
E ( x, t ) = E0 ⋅ sin( kx − ω t + ϕ )
B ( x, t ) = B0 ⋅ sin( kx − ω t + ϕ )
direzione (istantanea)
del vettore E
direzione di
propagazione
direzione (istantanea)
del vettore B
λ
Scale logaritmiche in potenze di 10
ν
(103)
(100)
(10-3)
(10-6)
(10-9)
(10-12)
700 nm
400 nm
Spettro delle onde elettromagnetiche
c =ν ⋅ λ
Generazione di onde elettromagnetiche
Oscillazioni in circuiti LC (alla frequenza
propria); cariche oscillanti in una antenna
(con un generatore di corrente alternata);
atomi eccitati ad alta temperatura (per la
luce); dipoli elettrici oscillanti
Densità di energia del campo elettrico u E = ε 0 E 2
Energia trasportata da un’onda e.m.
1
2
1 2
Densità di energia del campo magnetico u B =
B
2 µ0
1
1 2
B = uB
Dato che E = c B risulta u E = ε 0 c 2 B 2 =
2
2 µ0
Onda e.m. (polarizzata linearmente)
generata da un’antenna con un
generatore di corrente alternata
In un’onda e.m. le densità di energia
associate ai campi E e B sono uguali!
Densità di energia totale: uT = u E + u B = ε 0 E 2 = B 2 / µ0
è funzione dello spazio e del tempo, infatti
2
u T = ε 0 E 2 = ε 0 E0 ⋅ sin 2 (kx − ω t ) (E0 : ampiezza del campo )
Densità di energia efficace, mediata su un periodo T di
oscillazione (come per la potenza media, un fattore 1/2)
u media
1
=
T
∫
T
0
T
1
1
ε 0 E dt = ε 0 E0 2 ∫ sin 2 (kx − ωt ) dt = ε 0 E0 2
0
T
2
2
Come nasce un’onda e.m. dal
campo elettrico generato da cariche
oscillanti in un’antenna
Flusso di energia: energia che passa
attraverso un’unità di superficie
(perpendicolare alla direzione di
propagazione) nell’unità di tempo
⇒
Il flusso di energia S (a x fissato)
è una funzione del tempo,
proporzionale a sin2(kx-ωt) .
Rappresentato da un vettore S
diretto nel verso di propagazione
dell’onda e.m. , e di modulo
E2
S=
=
;
µ0 µ 0 c
EB
[S ] =
J
Watt potenza
=
=
2
2
s⋅m
m
area
Si definisce intensità I l’energia per unità di tempo e
di superficie, mediata su un periodo T di oscillazione
(come per la potenza media, un fattore 1/2)
1
1 1
1 1 2
2
=
=
S
dt
E
dt
E0
µ0 c T ∫0
µ0 c 2
T ∫0
T
I = Smedio =
Dato che µ0 =
T
1
ε0 c2
I = c ⋅ umedia
abbiamo
1
= c ⋅ ε 0 E02
2
Intensità = velocità · densità di energia media
Inoltre, dalla definizione, l’intensità è
anche una potenza emessa / superficie
I=
P
Area
S=
1
µ0
E×B
Vettore di Poynting
Esempio: onde sferiche, emesse da
una sorgente (quasi) puntiforme. Le
creste dell’onda sono superfici
sferiche. L’energia emessa per
unità di tempo (potenza P) si
ripartisce su un’area 4π
πr2 , quindi
l’intensità a distanza r vale
P
I=
4π r 2
(ancora la legge dell’inverso
del quadrato della distanza!)
r












