Alberi

Alberi
Definizioni principali
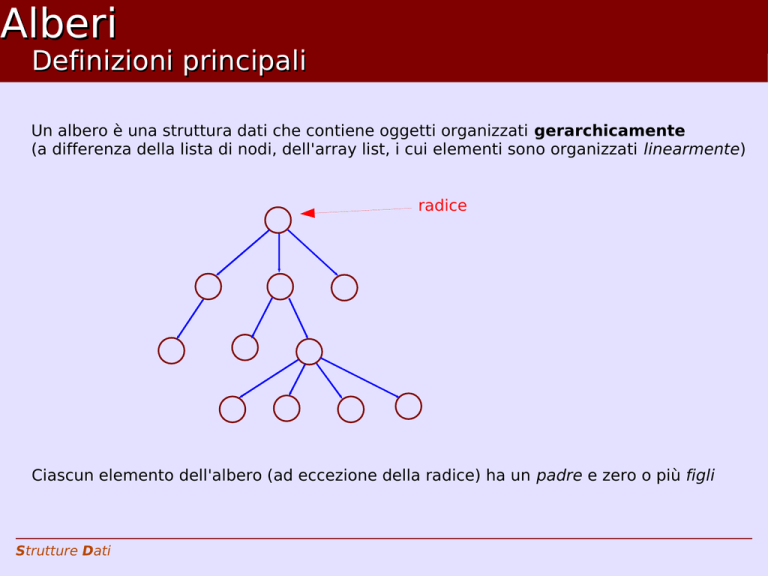
Un albero è una struttura dati che contiene oggetti organizzati gerarchicamente
(a differenza della lista di nodi, dell'array list, i cui elementi sono organizzati linearmente)
radice
Ciascun elemento dell'albero (ad eccezione della radice) ha un padre e zero o più figli
Strutture Dati
Alberi
Padre
Ciascun nodo v di T diverso dalla radice
ha un unico padre w
w
v
Strutture Dati
Alberi
Figli
w
Strutture Dati
Tutti i nodi che hanno w come padre
sono figli di w
Alberi
Fratelli
w
Tutti i nodi che sono figli dello stesso
padre sono detti fratelli
Strutture Dati
Alberi
Foglie
I nodi che non hanno figli sono chiamati
foglie
Strutture Dati
Alberi
Nodi interni
I nodi che hanno almeno un figlio sono
chiamati nodi interni
Strutture Dati
Alberi
Antenati e discendenti
Un nodo u è un antenato di un nodo v se:
u = v oppure
u è un antenato del padre di v
u
Un nodo v è un discendente di un nodo u se:
u è un antenato di v
w
v
Strutture Dati
Alberi
Sottoalberi
Un sottoalbero di un albero T radicato a v
è un albero che consiste di tutti i discendenti di v
v
Strutture Dati
Alberi
Profondità
La profondità di un nodo v è il numero di
antenati di v (escluso v)
Ricorsivamente:
v
Strutture Dati
2
●
●
se v è la radice, la profondità di v è 0
altrimenti la profondità di v è la
profondità del padre di v più 1
Alberi
Altezza
v
3
L'altezza di un nodo v è il massimo numero di
discendenti di v (escluso v) su un cammino
che va da v a una foglia
Ricorsivamente:
se v è una foglia, l'altezza di v è 0
● altrimenti l'altezza di v è la massima altezza
fra i figli di v più 1
●
Strutture Dati
Alberi
Visita preorder
La visita preorder di un albero T è una visita dei nodi di T che si può definire
ricorsivamente nel modo seguente:
- prima si visita la radice di T
- poi si fa una visita preorder per ciascuno dei sottoalberi radicati nei suoi figli
Strutture Dati
Alberi
Visita preorder
La visita preorder di un albero T è una visita dei nodi di T che si può definire
ricorsivamente nel modo seguente:
- prima si visita la radice di T
- poi si fa una visita preorder per ciascuno dei sottoalberi radicati nei suoi figli
Strutture Dati
Alberi
Visita preorder
La visita preorder di un albero T è una visita dei nodi di T che si può definire
ricorsivamente nel modo seguente:
- prima si visita la radice di T
- poi si fa una visita preorder per ciascuno dei sottoalberi radicati nei suoi
figli
Strutture Dati
Alberi
Visita preorder
La visita preorder di un albero T è una visita dei nodi di T che si può definire
ricorsivamente nel modo seguente:
- prima si visita la radice di T
- poi si fa una visita preorder per ciascuno dei sottoalberi radicati nei suoi
figli
Strutture Dati
Alberi
Visita preorder
La visita preorder di un albero T è una visita dei nodi di T che si può definire
ricorsivamente nel modo seguente:
- prima si visita la radice di T
- poi si fa una visita preorder per ciascuno dei sottoalberi radicati nei suoi
figli
Strutture Dati
Alberi
Visita postorder
La visita postorder di un albero T è una visita dei nodi di T che si può definire
ricorsivamente nel modo seguente:
- prima si fa una visita postorder dei sottoalberi radicati nei figli della radice
- poi si visita la radice di T
Strutture Dati
Alberi
Visita postorder
La visita postorder di un albero T è una visita dei nodi di T che si può definire
ricorsivamente nel modo seguente:
- prima si fa una visita postorder dei sottoalberi radicati nei figli della radice
- poi si visita la radice di T
Strutture Dati
Alberi
Visita postorder
La visita postorder di un albero T è una visita dei nodi di T che si può definire
ricorsivamente nel modo seguente:
- prima si fa una visita postorder dei sottoalberi radicati nei figli della radice
- poi si visita la radice di T
Strutture Dati
Alberi
Visita postorder
La visita postorder di un albero T è una visita dei nodi di T che si può definire
ricorsivamente nel modo seguente:
- prima si fa una visita postorder dei sottoalberi radicati nei figli della radice
- poi si visita la radice di T
Strutture Dati
Il tipo astratto di dati Albero
Tipo di dati e operazioni
Come l'ADT lista, anche l'ADT albero usa la nozione di posizione (position) per
memorizzare i suoi elementi
Anche qui un oggetto Position offre il seguente metodo:
element(): restituisce l'oggetto memorizzato in questa posizione
Strutture Dati
Il tipo astratto di dati Albero
Tipo di dati e operazioni
Metodi generici
size(): restituisce il numero dei nodi dell'albero
isEmpty(): verifica se l'albero è vuoto
iterator(): restituisce un iteratore degli elementi nei nodi dell'albero
positions(): restituisce un iteratore dei nodi dell'albero
Metodi di accesso
root(): restituisce la radice dell'albero; si verifica un errore se l'albero è vuoto
parent(v): restituisce il padre di v; si verifica un errore se v è la radice
children(v): restituisce un iteratore delle posizioni dei figli di v
Strutture Dati
Il tipo astratto di dati Albero
Tipo di dati e operazioni
Metodi di interrogazione:
isInternal(v): verifica se v è un nodo interno
isExternal(v): verifica se v è una foglia
isRoot(v): verifica se v è la radice
Metodi di modifica:
replace(v, e): rimpiazza con e l'elemento nel nodo v e restituisce il vecchio elemento
addRoot(e): aggiunge la radice (che conterrà l'elemento e) ad un albero vuoto
insertChild(v,e): aggiunge un nuovo figlio al nodo v (il nuovo figlio conterrà l'elemento e)
...
Strutture Dati
Il tipo astratto di dati Albero
Eccezioni
InvalidPositionException
ogni metodo che prende in input una posizione, lancia una InvalidPositionException
se questa posizione è invalida;
BoundaryViolationException
parent(v) lancia una BoundaryViolationException se il nodo v è la radice dell'albero;
EmptyTreeException
root() lancia una EmptyTreeException se invocato su un albero vuoto.
NonEmptyTreeException
addRoot(e) lancia una NonEmptyTreeException se invocato su un albero non vuoto.
Strutture Dati