La luce ha una velocita’ finita (un miliardo di km/ora).
Guardare lontano equivale a guardare nel passato.
Osservazioni
del passato remoto dell’ Universo
Esempi:
• Il Sole: dista 150
milioni di km, o 8
minuti
luce.
Lo
vediamo come era 8
minuti prima.
• La stella piu’ vicina:
la vediamo ora come
era 4.2 anni fa.
• La
galassia
di
Andromeda:
la
vediamo oggi come
era 2.2 milioni di anni
fa
• Alcune delle galassie
dell’ Hubble Deep
Field: le vediamo
oggi come erano circa
11 miliardi di anni fa
Paolo de Bernardis
Dipartimento di Fisica, Universita’ La Sapienza,
Roma, Italy
L’ Eredita’ di Einstein
Roma, Biblioteca Casanatense
24/11/2005
Si puo’ osservare ancora piu’ lontano,
e quindi ancora piu’ indietro nel tempo, cercando di
scoprire se c’e’ stata una nascita dell’ Universo ?
La risposta e’ “si, ma…”
Per rispondere dobbiamo considerare alcuni fatti non
banali, ed attingere a piene mani all’ eredita’ di Einstein
Edwin Hubble
Solo la teoria delle relativita’ generale permette di
spiegare le osservazioni cosmologiche moderne :
Espansione
dell’ universo
Relativita’ Generale
(teoria della
gravitazione)
Lenti Gravitazionali
Solo la teoria delle relativita’ generale permette di
spiegare le osservazioni cosmologiche moderne :
redshift
Big Bang
Caldo
Interazione tra
la luce e le masse
Legge di
Hubble
Espansione
dell’ universo
QSO
Fondo Cosmico
a Microonde
Relativita’ Generale
(teoria della
gravitazione)
Abbondanze
degli
elementi
Anisotropia del
fondo a microonde
George Gamow
Albert Einstein
Lenti Gravitazionali
redshift
Big Bang
Caldo
Interazione tra
la luce e le masse
Legge di
Hubble
QSO
Fondo Cosmico
a Microonde
Abbondanze
degli
elementi
Anisotropia del
fondo a microonde
1
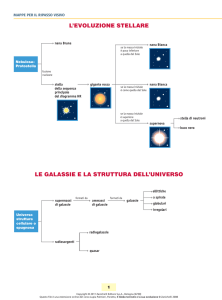
L’ espansione dell’
Universo
• La misure di Wirz e Hubble e’ basata su due diverse
osservazioni: di distanza (piu’ sono lontane, e meno
luminose appaiono le galassie) e di colore della luce
(spettro) .
• La luce e’ formata da onde elettromagnetiche. Il colore
della luce dipende dalla sua lunghezza d’ onda λ
λ
• Viviamo in un universo in
espansione, perche’ le
Galassie - i mattoni
costitutivi dell’ universo
visibile – si allontanano le
une dalle altre.
•A questa conclusione
giunsero Carl Wirtz ed
Edwin Hubble negli
anni 20-30, osservando
ed interpretando il fatto
che piu’ una galassia
e’ distante, piu’ la sua
luce e’ spostata verso
il colore rosso
(redshift)
Luce blu
λ
Luce rossa
0 ,0
Δλ/λ = v/c
Sorgente sonora o
luminosa in movimento
Questo osservatore vede
una lunghezza d’ onda
maggiore perche’ la sorgente
si sta allontanando
Redshift delle galassie
3 ,2
4 ,0
N(z)
velocita’ ricavata dal
redshift: v = c Δλ/λ
PSCz
Saunders et al.
MNRAS 2000
18351 galaxies
within 60 Mpc
2000
1000
0
0
20000
40000
cz (km/s)
v=c Δλ/λ
(km/s)
• Hubble interpreto’ lo spostamento verso il rosso
della lunghezza d’ onda della luce delle galassie
(il redshift) come un effetto Doppler, dovuto ad
un moto generale di allontanamento delle
galassie.
• Oggi sappiamo che il redshift e’ un fenomeno
molto piu’ profondo, che si spiega applicando la
relativita’ generale di Einstein al “fluido
cosmologico” di galassie.
• Intanto cerchiamo di capire meglio i dati
sperimentali.
• Riportando in grafico la velocita’ di allontanamento in funzione della
magnitudine (distanza) si osserva poi che piu’ le galassie galassie
sono lontane, maggiore e’ lo spostamento verso il rosso della loro
luce. Se la causa del redshift e’ l’ effetto doppler, le galassie piu’
lontane si allontanano piu’ velocemente da noi.
3000
Numero di galassie
2 ,4
Interpretazione del redshift
• Christian Doppler
dimostro’ nel 1843 la
dipendenza della
lunghezza d’ onda dal
moto relativo di
sorgente ed
osservatore.
• Tanto maggiore e’ la
velocita’ relativa,
tanto maggiore e’ lo
spostamento della
lunghezza d’ onda
misurata:
Se si tratta di
effetto Doppler,
le Galassie
lontane sembrano
tutte allontanarsi
da noi.
1 ,6
• L’ effetto Doppler, dovuto alla velocita’ relativa di
sorgente e osservatore, altera la lunghezza d’ onda della
luce, trasformando un colore in un altro.
Effetto Doppler
Lo spostamento
delle lunghezze d’
onda e’ sempre
positivo (almeno
per le galassie
lontane)
0 ,8
d is t a n z a ( m ili o n e s im i d i m e t r o )
6000
distanza
• La costante di proporzionalita’ tra velocita’ di allontanamento e
distanza e’ detta costante di Hubble:
Ho ~ 70 (km/s) / (Mpc)
2
Conseguenze dell’ espansione:
Esempio del panettone che
lievita.
Il panettone prima della lievitazione ha
un diametro di 20 cm; dopo 2 ore in
forno ha un diametro di 40 cm.
Indichiamo con una freccia la nostra
uvetta di riferimento.
L’ uvetta che inizialmente era a 5 cm
dalla nostra, dopo 2 ore si trova a 10 cm Distanza doppia implica
dalla nostra. La sua velocita’ di
velocita’ doppia di
allontanamento e’ di 2.5 cm/ora.
allontanamento: la Legge
di Hubble e’ conseguenza
L’ uvetta che inizialmente era a 10 cm naturale di una espansione
dalla nostra, dopo 2 ore si trova a 20 cm isotropa dello spazio.
dalla nostra. La sua velocita’ di
Avrei potuto scegliere un’
allontanamento e’ di 5 cm/ora.
altra uvetta di riferimento!
• Guardare lontano implica
osservare oggetti che si stanno
allontanando sempre piu’
velocemente da noi.
• Tanto che la loro emissione, per
il redshift , ha lunghezze d’
onda sempre piu’ lunghe.
• Dal visibile si sposta nel rosso,
poi nell’ infrarosso, poi nelle
microonde !
• Non la vediamo piu’, almeno
con l’ occhio e con i rivelatori di
luce visibile !
Conseguenze dell’ espansione:
20000 QSO nella
2dF redshift survey
z del QSO
• Osservando luce IR,
oppure osservando
luce UV, che viene
spostata nel visibile
dal redshift, si scopre
che lo spostamento
verso il rosso puo’
essere sostanziale.
• Per i QSO, ma anche
per galassie normali si
puo’ avere z=Δλ/λ>1
o >>1.
Ly-α
(0.1216μm)
@
1.3μm:
z = 10 !
λ osservata
• Se fosse un effetto Doppler classico, la
sorgente si starebbe allontanando a 9 volte
la velocita’ della luce.
Ly-α
(0.1216μm) • Si puo’ usare la formula dell’ effetto
Doppler relativistico, concludendo che la
@
sorgente si allontana al 98.4% della
1.3μm:
velocita’ della luce (!!).
• L’ approccio corretto e’ quello della
relativita’ generale. E’ lo spazio stesso (la
z = 10 ! metrica) che si sta espandendo,
trascinando con se’ tutte le galassie : e’ un
moto H=1.63μm
con lo spazio,
non attraverso lo
R=0.8μm J =1.25μm
K =2.2μm
spazio.
• L’ espansione allunga tutte le lunghezze,
comprese le lunghezze d’ onda dei fotoni.
R=0.8μm
J =1.25μm
H=1.63μm K =2.2μm
• La relativita’ generale di Einstein ci
spiega che in un universo in espansione
le lunghezze d’onda dei fotoni si
allungano esattamente quanto le altre
lunghezze.
• E’ l’ espansione dello spazio che allunga
anche le lunghezze d’ onda: luce che
viene emessa blu, con l’ espansione
diventa rossa e poi infrarossa. Piu’ e’
lungo il cammino e piu’ la lunghezza d’
onda viene allungata.
• Per questo le sorgenti lontanissime hanno
redshift maggiore di 1. In termini general
relativistici vuol solo dire che l’ universo
si e’ allargato di piu’ di 2 volte dal
momento dell’ emissione a quello della
ricezione.
L.B.
t =13 Gy
Il redshift
to
t1
t2
Doppler: Δλ/λ = v/c
Einstein: Δλ/λ=ΔL/L=z
λ/λο=L/Lo= 1+z
3
• Perche’ non vediamo sorgenti
ancora piu’ lontane?
• Una delle conquiste della
cosmologia moderna e’ il fatto che
tutte le componenti dell’ universo
evolvono.
• Le galassie piu’ lontane sono molto
diverse da quelle piu’ vicine, e
questo e’ dovuto all’ evoluzione.
Questo significa che le galassie sono
nate in una certa epoca remota.
• La Galassia record a z=10 e’ un
oggetto molto piu’ piccolo di una
Galassia normale. Potrebbe essere
uno dei “mattoni” primordiali da cui
si sono poi formate le galassie.
• L’ universo primordiale e’ l’
universo prima della formazione
delle Galassie.
• I cosmologi fissano l’ epoca della
formazione delle galassie ad un
redshift tra 10 e 20.
• Questo significa anche che l’
universo era molto piu’ semplice
ed omogeneo nelle sue fasi
primordiali
• Dall’ universo omogeneo iniziale si
sono lentamente formate le strutture
grazie all’ azione aggregatrice della
gravita’.
Solo la teoria delle relativita’ generale permette di
spiegare le osservazioni cosmologiche moderne :
Espansione
dell’ universo
Relativita’ Generale
(teoria della
gravitazione)
redshift
Big Bang
Caldo
Interazione tra
la luce e le masse
Legge di
Hubble
QSO
Fondo Cosmico
a Microonde
Abbondanze
degli
elementi
Anisotropia del
fondo a microonde
Lenti Gravitazionali
• George Gamow negli anni 50
dimostro’ che l’ universo iniziale
Il
doveva anche essere piu’ caldo,
creando cosi’ la teoria del Big Bang
Caldo.
• Un gas isolato che si espande si
raffredda. L’ universo e’ un sistema
isolato in espansione, e fa la stessa
cosa.
• Piu’ indietro andiamo nel tempo, piu’
caldo doveva essere l’ universo.
• Se guardiamo abbastanza lontano,
osserveremo un’ epoca talmente
remota che tutto l’ universo era caldo
come il sole.
Granulazione solare
Granulazione solare
Gas incandescente
sulla superficie del
Sole (5500 K)
Qui, ora
8 minuti luce
Big Bang
Caldo
Gas incandescente
sulla superficie del
Sole (5500 K)
Qui, ora
8 minuti luce
Gas incandescente
nell’ universo
primordiale (l’
universo diventa
trasparente a 3000 K)
Qui, ora
14 miliardi di anni luce
Mappa di BOOMERanG dell’ Universo Primordiale
4
• Come non si puo’ guardare dentro il Sole, che e’
opaco, non si puo’ guardare come era l’ universo
quando era piu’ caldo di qualche migliaio di gradi.
• Ci e’ preclusa l’ osservazione diretta dei primi
380000 anni dell’ universo, il tempo che ci mette a
raffreddarsi fino a 3000 gradi.
• 380000 anni rispetto a 14 miliardi di anni di eta’
attuale non e’ male… ma vedremo poi che
indirettamente si possono studiare anche i primi
attimi.
• La luce piu’ antica che possiamo osservare e’
quella proveniente da quella fase in cui tutto l’
universo era incandescente.
• Come vediamo luce arrivare dalla superficie
incandescente del sole, dobbiamo aspettarci
arrivare luce da quell’ epoca dell’ Universo.
• Solo che nel frattempo l’ universo si espande circa
1000 volte, e la lunghezza d’ onda della luce
diventa alcuni millimetri.
• Ci aspettiamo quindi delle microonde.
• Queste sono state osservate davvero, e’ il fondo
cosmico a microonde.
Il fondo cosmico a microonde
COBE-FIRAS
• Negli anni successivi il fondo
cosmico e’ stato osservato a
tutte le lunghezze d’ onde da
meno di 1 GHz a circa 1000
GHz.
• Nel 1992 l’ esperimento FIRAS
sul satellite COBE ha
dimostrato che lo spettro e’
esattamente di corpo nero
(deviazioni inferiori a una parte
su 10000 !)
• Il fondo a microonde fu
osservato per la prima
volta per caso da Arno
Penzias e Robert Wilson,
nel 1965.
• Lavorando ad una antenna
per trasmissioni della Bell
scoprirono la presenza di
un “rumore di fondo”,
indipendente dalla
direzione del cielo
osservata.
I fisici del gruppo di Princeton capirono che il rumore
di fondo misurato da Penzias e Wilson altro non era che
la radiazione proveniente dall’ universo primordiale
Fondo a microonde e nucleosintesi
• Se la radiazione di corpo nero a
2.725K riempie tutto l’ universo,
vuol dire che ci sono 400 fotoni
per ogni cm3 di universo.
• La maggior parte dei fotoni dell’
universo e’ in questa forma.
• E ci sono circa un miliardo di
fotoni per ogni particella massiva.
• Gamow calcolo’ i nuclei di elio potevano formarsi nell’ universo
primordiale a partire da protoni e neutrini, a patto che fosse
presente una grande quantita’ di fotoni, che dovevano essere
presenti come radiazione termica ancora oggi ad una temperatura
di pochi K. (Nucleosintesi)
• E’ esattamente quanto si osserva !
Solo la teoria delle relativita’ generale permette di
spiegare le osservazioni cosmologiche moderne :
Espansione
dell’ universo
Relativita’ Generale
(teoria della
gravitazione)
Lenti Gravitazionali
redshift
Big Bang
Caldo
Interazione tra
la luce e le masse
Legge di
Hubble
QSO
Fondo Cosmico
a Microonde
Abbondanze
degli
elementi
Anisotropia del
fondo a microonde
5
Solo la teoria delle relativita’ generale permette di
spiegare le osservazioni cosmologiche moderne :
Espansione
dell’ universo
Relativita’ Generale
(teoria della
gravitazione)
Lenti Gravitazionali
Solo la teoria delle relativita’ generale permette di
spiegare le osservazioni cosmologiche moderne :
redshift
Big Bang
Caldo
Interazione tra
la luce e le masse
Legge di
Hubble
Espansione
dell’ universo
QSO
Relativita’ Generale
(teoria della
gravitazione)
Fondo Cosmico
a Microonde
Abbondanze
degli
elementi
redshift
QSO
Fondo Cosmico
a Microonde
Big Bang
Caldo
Interazione tra
la luce e le masse
Anisotropia del
fondo a microonde
Legge di
Hubble
Abbondanze
degli
elementi
Anisotropia del
fondo a microonde
Lenti Gravitazionali
Interazione tra luce e gravita’
• Secondo la relativita’ generale le masse interagiscono con la luce,
deflettendola e cambiando la sua frequenza.
• Questi effetti si possono derivare in modo semplice dalle
fondamenta della teoria, cioe’ dal principio di equivalenza:
• Tutti i laboratori in caduta libera e non rotanti sono
completamente equivalenti per tutti gli esperimenti fisici
(Einstein, 1907).
• La caduta libera e’ un modo per eliminare gli effetti visibili
localmente della gravita’, l’ assenza di rotazione elimina gli effetti
delle forze apparenti
• Secondo l’ esempio dell’ ascensore di Einstein: “una persona in un
ascensore in caduta libera non sente il proprio peso, e non puo’
capire se l’ ascensore si trova sulla terra ed e’ in caduta libera,
oppure se si trova nello spazio lontano da altre masse”.
• Viceversa …
Curvatura delle traiettorie luminose
Interazione tra luce e gravita’
• Possiamo costruire due esperimenti concettuali che ci permettono di
valutare la portata del principio di equivalenza, e di stabilire che l’
interazione gravitazionale deve agire anche sulla luce.
• Esperimento 1:
• Montiamo nell’ ascensore un laser in modo che il fascio di luce
emesso sia orizzontale, e lasciamo cadere l’ ascensore.
• La gravita’ e’ stata “abolita” nell’ ascensore, e per il principio d’
equivalenza l’ osservatore nell’ ascensore vedra’ il raggio di luce
propagarsi lungo una linea retta parallela al pavimento dell’
ascensore.
• Ma se questo e’ vero, l’ osservatore a terra, dove la gravita’ si sente,
vedra’ il raggio di luce percorrere una curva ! Dalla composizione del
moto orizzontale della luce x=ct e del moto dell’ ascensore
z=-(1/2)gt2 vediamo subito che il moto del raggio di luce nel
riferimento terrestre e’ una parabola (moto di un proiettile).
• La presenza di gravita’ deflette la traiettoria del raggio di luce.
z
t=0
z
t=l/c
l
1 2
gt
2
l
x
• L’ angolo di deflessione e’ dell’ ordine di
x
1 2
gt
gl 10m / s 2 × 10m
ϕ≈ 2
≈ 2 ≈
≈ 10 −15 rad ≈ 2 × 10 −10 arcsec
l
c
(3 × 108 m / s )2
• Decisamente un esperimento concettuale !
6
Misure di Deflessione della Luce
• La misura della deviazione dei raggi di
luce provenienti dalle stelle lontane a
causa della curvatura dello spazio
dovuta al campo gravitazionale del Sole
fu la prima prova della teoria
sperimentale della relativita’ generale
di Einstein.
• Eddington (1917) uso’ raggi di stelle
che passano molto vicino al sole. In
quel caso, l’ effetto e’ di pochi secondi
d’ arco.
• Con la precisione di Hipparcos, mille
volte superiore, e’ possibile rivelare l’
effetto anche per stelle a 90o dalla
direzione del sole, cioe’ su decine di
migliaia di stelle del catalogo
principale, ottenendo cosi’ una elegante
verifica della relativita’ generale.
La presenza di massa curva i raggi di luce !
1”
Sole
Luna (eclisse)
Terra
QSO
galassia
Qui
• Il fenomeno e’
ormai usuale
nelle immagini
dell’ Hubble
Space
Telescope. Le
sorgenti
lontane
appaiono
deformate a
causa delle
masse
interposte
• Lenti
Gravitazionali
1”
sole
terra
Archi
Anello di Einstein
Immagini Multiple
Solo la teoria delle relativita’ generale permette di
spiegare le osservazioni cosmologiche moderne :
Espansione
dell’ universo
Relativita’ Generale
(teoria della
gravitazione)
Lenti Gravitazionali
Magnificazione
redshift
Big Bang
Caldo
Interazione tra
la luce e le masse
Legge di
Hubble
QSO
Fondo Cosmico
a Microonde
Abbondanze
degli
elementi
Anisotropia del
fondo a microonde
7
Solo la teoria delle relativita’ generale permette di
spiegare le osservazioni cosmologiche moderne :
Espansione
dell’ universo
Relativita’ Generale
(teoria della
gravitazione)
redshift
QSO
Big Bang
Caldo
Interazione tra
la luce e le masse
Legge di
Hubble
Fondo Cosmico
a Microonde
Abbondanze
degli
elementi
z
t=0
h
x
Anisotropia del
fondo a microonde
Lenti Gravitazionali
• Esperimento 2:
Interazione tra luce e gravita’
• Ma per l’ osservatore a terra, il
rivelatore si sta avvicinando verso il
raggio di luce. All’ arrivo della luce,
dopo un tempo h/c, il rivelatore ha z
guadagnato una velocita’ v=gt=gh/c
verso il raggio di luce.
t=h/c
• Quindi dovrebbe vedere una
frequenza spostata verso il blu di
Δν/νο=v/c=gh/c2 .
h
• Se il principio di equivalenza e’
vero, questo non puo’ succedere.
• Dobbiamo supporre che la gravita’
tenda a diminuire la frequenza della
x
luce quando diminuisce il potenziale
gh
Δφ
Δν
gravitazionale, compensando il
=− 2 =− 2
νo
c
c
blueshift: redshift gravitazionale.
Torniamo ora alla CMB: se nel plasma primordiale ci sono
fluttuazioni di densita’, noi vedremo fluttuazioni della Temperatura
del fondo a microonde dovute a 2 effetti:
Le zone sovradense sono anche piu’ calde, quindi c’e’ una maggiore
energia dei fotoni che provengono da esse.
Tuttavia questi fotoni perdono un po’ di energia perche’ si
allontanano da una massa e quindi subiscono un redshift
gravitazionale.
Gas incandescente
nell’ universo
primordiale (l’
universo diventa
trasparente a 3000 K)
Qui, ora
Interazione tra luce e gravita’
• Esperimento 2:
• Stavolta montiamo sul
pavimento dell’ ascensore un
laser con frequenza νo in modo
che il fascio di luce emesso sia
diretto verso l’ alto, e lasciamo
cadere l’ ascensore.
• La gravita’ e’ stata “abolita”
nell’ ascensore, e per il
principio d’ equivalenza un
rivelatore posto sul soffitto
registrera’ , all’ arrivo della
luce, la stessa frequenza νo .
Redshift Gravitazionale
Δν
νo
=−
gh
c2
• Questo esperimento e’ stato fatto davvero nel 1960 sulla torre dell’
universita’ di Harvard (h=22.6m) da Pound e Rebka.
• Nel loro esperimento hanno usato una sorgente di raggi gamma
(quindi frequenza νο altissima), e hanno rivelato il minuscolo
spostamento di frequenza grazie all’ effetto Mossbauer.
Δν
νo
=−
gh
= − 2 .5 × 10 −15
c2
• Si puo’ misurare solo perche’ la riga gamma ha una larghezza
estremamente piccola.
Le zone sovradense sono anche piu’ calde, quindi c’e’ una
maggiore energia dei fotoni che provengono da esse.
Tuttavia questi fotoni perdono un po’ di energia perche’ si
allontanano da una massa e quindi subiscono un redshift
gravitazionale.
Questi due effetti si compensano solo parzialmente. Quindi
realizzando una mappa della temperatura della CMB possiamo
vedere quali erano le protostrutture (fluttuazioni di densita’)
presenti nell’ universo a quell’ epoca remota (14 miliardi di anni
fa).
ΔT
Δφ
=− 2
T
3c
14 miliardi di anni luce
Mappa di BOOMERanG dell’ Universo Primordiale
8
Immagini dell’ Universo Primordiale
• L’ esistenza della radiazione cosmica di fondo e’
quindi una conferma sperimentale della teoria del Big
Bang Caldo: viviamo in un universo in espansione,
che deve provenire da uno stadio iniziale
enormemente caldo e denso
• Abbiamo quindi a disposizione luce che arriva da un’
epoca di “appena” 380000 anni dopo il big bang,
quando l’ universo era 1000 volte piu’ piccolo, 1000
volte piu’ caldo, un miliardo di volte piu’ denso e
50000 volte piu’ giovane di oggi.
• Se riusciamo ad ottenere un’ immagine di questa
radiazione, abbiamo un’ immagine dell’ universo
primordiale, all’ epoca piu’ antica investigabile con la
luce. E’ una sfida per gli sperimentatori fin dal 1965!
COBE-DMR
• Sul satellite COBE (1992)
erano presenti dei radiometri
differenziali (DMR), costruiti
per ottenere una immagine della
radiazione cosmica di fondo
dall’ esterno dell’ atmosfera
terrestre.
• L’ immagine e’ estremamente
poco contrastata. Ma esistono
davvero delle strutture, ad un
livello di 10 parti per milione !.
• Le tre mappe a tutto cielo
riportate a fianco differiscono a
causa del rumore dei rivelatori.
• Siccome DMR non aveva un
vero e proprio telescopio, le
strutture piu’ grandi
distinguibili nelle mappe hanno
dimensioni di circa 10 gradi.
Non e’ sufficiente !
anisotropie
Le misure di anisotropia
• Fin dagli anni 70 fu chiaro che l’ immagine
della radiazione cosmica di fondo era
estremamente poco contrastata.
• La radiazione di fondo e’ con ottima
approssimazione isotropa.
• Le anisotropie (variazioni di temperatura da
una zona all’ altra del cielo) sono inferiori a
100 parti per milione (300 milionesmi di
grado o 300 μK) a qualunque scala angolare
inferiore a 90 gradi.
• Le misure sono estremamente difficili, a causa
dell’ emissione (10 K) e delle fluttuazioni di
emissione (10 mK) dell’ atmosfera terrestre,
molto maggiori del segnale da misurare.
• Le misure vanno fatte in alta montagna, o in
Antartide, o da palloni stratosferici o da
satelliti in orbita.
“Notte stellata”, vista da:
1o
Piano della Galassia
(risoluzione 12’)
Piano della Galassia
Piano della Galassia
Un vero telescopio per il fondo cosmico
• E’ necessario un esperimento con risoluzione migliore di
un grado per poter fare la misura.
• Per ottenere la risoluzione, si deve costruire un vero e
proprio telescopio per microonde, che permettera’:
• di vedere l’ Universo primordiale
• di studiare e vedere le protostrutture, i semi da cui
nasceranno le galassie, nella loro fase iniziale
• di determinare la geometria dell’ universo, e quindi la sua
evoluzione passata e futura
• di determinare la densita’ totale di massa ed energia, con
la quale va confrontata la somma di tutte le componenti
note (materia luminosa, materia oscura, energia oscura) per
vedere se il totale torna….
http: // oberon.roma1.infn.it / boomerang
http: // www.physics.ucsb.edu / ~boom
(risoluzione 7o)
9
L’ arrivo di BOOMERanG / fine Ottobre 1998
• L’ immagine
del cielo deve
essere
costruita
pazientemente,
osservando
una direzione
alla volta e
registrando i
dati
• La scansione
deve essere
molto dolce e
costante (da 1
a 2 gradi al
secondo)
La scansione del cielo
avo o d asse b agg o e test de o st u e to a W
a
ed
Nov. 98
Lavoro di assemblaggio e test dello strumento a William Field – Nov. 98
Lavoro di assemblaggio e test dello strumento a William Field – Nov. 98
10
Lavoro di assemblaggio e test dello strumento a William Field – Nov. 98
Il lancio: 29/12/1998
Il lancio – 29 dic. 98
Il lancio – 29 dic. 98
Il lancio: 29/12/1998
Il viaggio fortunato della
navicella: a 37 Km di
quota, in balia delle
correnti a getto, ha
circumnavigato
l’ Antartide per tornare,
dopo 8000 km di viaggio,
vicino alla base di lancio.
L’ 8/1/1999, mentre
sorvolava il pack vicino
alla base, abbiamo
inviato il telecomando
di separazione.
Il giorno successivo
abbiamo potuto recuperare
la navicella.
11
Qual’e’ la geometria dell’ Universo ?
Spazio Piatto in 2 dimensioni
• Anche nel caso dell’
universo nel suo insieme, a
grande scala, la relativita’
generale ci assicura che
massa ed energia presenti
nell’ universo curvano lo
Spazio Piatto in 3 dimensioni
spazio.
• Solo se la densita’ dell’
universo e’ esattamente pari
a quella critica lo spazio
non e’ curvo, e’ il normale
spazio Euclideo, in cui due
raggi di luce che partono
paralleli non si incontrano
mai
Qual’e’ la geometria dell’ Universo ?
• Ma se la densita’ e’
superiore a quella critica,
lo spazio viene curvato.
Due raggi di luce che
partono paralleli prima o
poi si incontrano.
• Non e’ strano: l’ analogo
bidimensionale sono i
paralleli terrestri, che
partono paralleli dall’
equatore, ma si incontrano
al polo !
Qual’e’ la geometria dell’ Universo ?
Spazio Curvo in 2 dimensioni
(curvatura positiva)
Spazio Curvo in 3 dimensioni
(curvatura positiva)
• Se invece la densita’ e’
inferiore a quella critica,
lo spazio viene curvato
nell’ altra direzione. Due
raggi di luce che partono
paralleli divergono.
• L’ analogo bidimensionale
sono linee tracciate su una
sella invece che su una
sfera
Spazio curvo in 3 dimensioni
(curvatura negativa)
Le dimensioni delle strutture
nella radiazione di fondo
Universo con densita’ critica
Ω=1
Universo con densita’ alta
Spazio curvo in 2 dimensioni
(curvatura negativa)
Ω>1
Universo ad alta densita’
Ω>1
2o
Universo a densita’critica
Ω=1
Universo a bassa densita’
Ω<1
1o
0.5o
Universo con densita’ bassa
Ω<1
12
Di che dimensioni sono le strutture
osservate ?
• Esiste una procedura
matematica, chiamata
spettro di potenza, che
permette di rispondere
alla domanda,
calcolando qual’ e’ l’
abbondanza delle
macchie di diverse
dimensioni.
• Questa puo’ essere
confrontata con la teoria
• La maggior parte delle
macchie hanno
dimensioni intorno ad 1
grado, come previsto per
una geometria
Euclidea, o piatta, dell’
Universo.
• quindi Ω=1 !
Chi crea le strutture ? Inflation !
Conseguenze per la Cosmologia
• L’ Universo ha una geometria Euclidea, quindi
secondo la relativita’ generale Ω=1
• Ma la materia visibile fornisce una densita’ pari
al 5% di quella critica, e quella oscura, secondo
i dati piu’ recenti, e’ dell’ ordine del 30%.
Qundi dovrebbe essere Ω =0.35.
• Manca all’ appello un 65% di massa o di
energia !
• Le misure di Supernovae lontane le trovano
piu’ deboli di quanto ci si aspetta. Forse l’
universo sta accelerando la sua espansione ? In
tal caso, il 65% di massa/energia mancante
potrebbe essere costituito da energia oscura
repulsiva, la famosa costante cosmologica
prima inventata e poi ripudiata da Einstein.
• Gli specialisti hanno denominato questa forma
di energia “energia oscura”
Tr
an
di sizio
fa ne
se
Dimensioni subatomiche
T=10-32s
Fluttuazioni quantistiche
del brodo primordiale
Energie tipiche:
1016 GeV
(100 milioni di miliardi
di milardi di eV)
UNA FINESTRA SUI
10 milioni di anni luce
PRIMI ISTANTI E
T=300000 anni
SULLA FISICA DELLE
Fluttuazioni di densita’
ALTISSIME ENERGIE illuminate dalla luce del fondo cosmico
Bolometri sensibili alla
polarizzazione
Previsioni dell’ inflazione cosmica:
• La geometria a grande scala deve essere
euclidea
• Le fluttuazioni di densita’ devono essere
uguali a tutte le scale
• Le fluttuazioni di temperatura devono
essere gaussiane
• Si genera un fondo di onde gravitazionali
Le prime tre sono consistenti con i dati di
BOOMERanG e di altri esperimenti. L’
ultima e’ tutta da verificare. Ci stiamo
lavorando !
3 μm thick
wire grids,
Separated by
60 μm, in the
same groove
of a circular
corrugated
waveguide
Planck-HFI
testbed
13
06/01/2003
• Planck is a satellite
launched in the
lagrangian point L2
of the Earth-Sun
system, 1.5Mkm
away from the
Earth, beyond the
moon orbit.
• From this advantage
location it will map
the Universe with
unprecedented
sensitivity and
resolution in the
range 20-800 GHz
(http://oberon.roma1.infn.it/olimpo)
OLIMPO
An arcmin-resolution
survey of the sky
at mm and sub-mm
wavelengths
Silvia Masi
Dipartimento di Fisica
La Sapienza, Roma
and
the OLIMPO team
Per saperne di piu’
• http://oberon.roma1.infn.it/boomerang
• Sulla Cosmologia, a livello introduttivo
– Livio Gratton: Origine ed evoluzione dell’ Universo – NIS
– Steven Weinberg: I primi tre minuti – Oscar Mondadori
• Su BOOMERanG, a livello introduttivo
– P. de Bernardis, S. Masi “Un click sull’ Universo”
Sapere, Giugno 2000 , pag.44-57
– P. de Bernardis, S. Masi “BOOMERanG e la nuova immagine
dell’ Universo” Sapere, Agosto 2001 , pag.78-82
– P. de Bernardis, S. Masi “BOOMERanG e la nuova
cosmologia”, Analysis, 4/2003
http://www.analysis-online.net/2003_4dic03.html
• Su Particelle Elementari e Cosmologia (introduttivo)
– B. Greene – L’ Universo Elegante – Einaudi
• Sui telescopi
– R. Panek - Vedere per credere – Tascabili Einaudi
14