Lezioni di ottica fisica: lezione n.2 seconda parte
Alessandro Farini
12 gennaio 2007
1
1.1
Interferenza
Sovrapposizione di onde
Consideriamo cosa accade quando due sistemi di onde si incrociano in una zona dello spazio e gli
effetti che si generano. Tutti gli effetti si possono interpretare mediante una legge che afferma che
lo spostamento risultante in ogni punto è pari alla somma degli spostamenti dovuti separatamente
ad ognuna delle onde. Questo principio è detto principio di sovrapposizione, e la sua prima formulazione e’ dovuta a Young. Questo spiega perche’ le onde, una volta attraversata la zona in
cui si sovrappongono, proseguono invariate, permettendo cosi’ ad esempio la visione degli oggetti
attraverso una stretta feritoia.
1.2
Sovrapposizione di due onde monocromatiche
Il campo elettrico di un’onda puo’ sempre essere visto come un vettore. La somma di due campi
~1 e E
~ 2 sara’ la loro somma vettoriale
elettrici E
~ =E
~1 + E
~2
E
Nel seguito consideriamo per semplicita’ che i due campi abbiano la stessa frequenza ω e che lo
spostamento dovuto ai due campi avvenga sulla stessa retta.
Avremo quindi
E1 = E01 sin(ωt − α1 )
(1)
E2 = E02 sin(ωt − α2 )
(2)
~ come
Per il principio di sovrapposizione possiamo scrivere l’ampiezza E0 del vettore risultante E
E0 = E01 sin(ωt − α1 ) + E02 sin(ωt − α2 )
1
qui si puo’ inserire il conto necessario per pervenire alle formule successive. Con alcuni
conti trigonometrici si puo’ scrivere che
2
2
E02 = E01
+ E02
+ 2E01 E02 cos(α1 − α2 )
(3)
Particolarmente interessante e’ il caso in cui le due ampiezze dei campi elettrici di partenza sono
uguali (E01 = E02 = Ep ). Dalla eq.(3) segue, una volta definita la differenza di fase (α1 − α2 ) = δ
E02 = 2Ep2 (1 + cos δ) = 4Ep2 cos2
δ
2
Dal momento che l’intensita’ di energia trasportata da un’onda e’ proporzionale al quadrato dell’ampiezza possiamo scrivere che per l’onda risultante
I ∼ E02 = 4Ep2 cos2
δ
2
(4)
Nel seguito considereremo I = E02 . L’intensita’ di ciascuna delle onde di partenza e’ pari a Ep2 .
Eppure osservando la precedente equazione ci si accorge che il valore massimo ottenibile per l’intensita’ dell’onda risultante e’ 4Ep2 (con δ = k 2π), valore piu’ grande della semplice somma algebrica
delle due intensita’ di partenza. D’altro canto per altri valori di δ (δ = π + k 2π) abbiamo che l’intensita’ risultante si annulla. La modificazione di intensita’ dovuta alla sovrapposizione di due onde
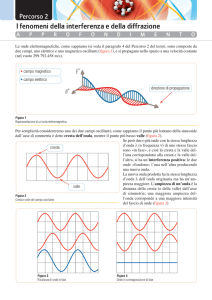
prende il nome di interferenza. Quando l’intensita’ risultante e’ massima parleremo di interferenza
costruttiva, quando si annulla di interferenza distruttiva (Fig.1) .
Figura 1: interferenza distruttiva e costruttiva: figura tratta da wikipedia versione inglese
1.3
L’Esperimento di Young
Uno dei primi esperimenti volti a mettere in evidenza dal punto di vista quantitativo l’interferenza
della luce fu quello effettuato da Young.
E’ un esperimento che mette in risalto l’interferenza di due fasci di luce. Perche’ l’effetto di interferenza sia piu’ evidente e’ necessario, come detto nella precedente sezione, che le due onde
siano entrambe monocromatiche. Inoltre i risultati precedenti sono stati ottenuti imponendo che
l’ampiezza delle due onde sia la stessa. Per realizzare tali condizioni si prende una sorgente di luce
monocromatica e la si manda contro uno schermo in cui e’ stata praticata una fenditura (Fig.2).
2
Dopo la fenditura si otterranno delle onde cilindriche, che vanno a colpire uno schermo su cui sono praticate due fenditure. Tali due fenditure sono le sorgenti adatte per il nostro esperimento.
Infatti, essendo originate da un’unica sorgente, sono sicuramente della stessa ampiezza. Inoltre
quando le onde partono dalle due fenditure hanno la stessa fase, a patto che la fenditura singola
sia equidistante dalle due, eguagliando cosi’ il cammino ottico.
Figura 2: apparato sperimentale dell’esperimento di Young
Se si va ad osservare tramite uno specchio la zona in cui le onde prodotte da queste due sorgenti
si sovrappongono si osserva un sistema di bande, cioe’ delle frange alternativamente chiare e scure
ugualmente distanziate (figura 3). Queste frange, dette appunto di interefrenza, possono essere
spiegate grazie all’equazione (4)
Figura 3: Immagine di frange prodotte dall’esperimento di Young
Per spiegare la formazione di frange ricorriamo alla costruzione geometrica riportata in figura 4
Vogliamo calcolare l’intensita’ dell’onda risultante nel punto P , ricorrendo alla formula 4. E’
quindi necessario calcolare la differenza di fase δ tra le due onde nel punto P . Dal momento che
consideriamo che l’esperimento si svolga tutto in aria possiamo considerare l’indice di rifrazione pari
a 1. Conseguentemente la differenza di fase e’ pari al prodotto per il numero d’onda k moltiplicato
3
Figura 4: Esperimento di Young: costruzione geometrica
4
per il cammino fisico, che in questo caso coincide con il cammino ottico:
δ = k∆ =
2π
(S2 P − S1 P )
λ
(5)
Il problema si riduce quindi a calcolare la differenza di percorso tra le due onde dopo l’attraversamento delle due fenditure. Preso il punto A in modo tale che S1 P = A P abbiamo che la differenza
di cammino e’ data dal segmento S2 A. Se la distanza D tra i due schermi e’ molto piu’ grande
della distanza tra le fenditure d allora si possono considerare uguali i due angoli θ e θ0 , da cui la
differenza di cammino ∆ risulta essere pari a d sin θ0 ' d sin θ. Inoltre poiche’ l’angolo θ e’molto
piccolo si puo’ confondere il seno dell’angolo con la sua tangente, da cui sin θ ' x/D. Possiamo
quindi scrivere la differenza di cammino
∆ = d sin θ = d
x
D
e inserirla nella eq.(5)per ottenere i valori di δ da cui
δ = d sin θ =
2π x
d
λ D
La eq.(4) ci mostra che i massimi dell’intensita’ si hanno per valori di δ = 2 kπ. Confrontata con
la 5 una tale condizione equivale ad avere la differenza di cammino uguale a un multiplo intero di
λ:
xd
= 0, λ, 2λ, 3λ, . . . = mλ
D
cioe’
D
x = mλ
d
In questi casi si ha il massimo di intensita’ e di conseguenza la presenza per quella coordinata x di
frange chiare. Il valore minimo dell’intensita’ si ha invece per δ = π + 2 kπ, il che equivale a
xd
λ 3λ 5λ
1
= 0, ,
,
, . . . = (m + )λ
D
2 2
2
2
cioe’
1 D
x = (m + )λ
2 d
Nelle precedenti equazioni m e’ un numero intero che puo’ assumere tutti i valori positivi a partire
da 0 ed e’ detto ordine. Di conseguenza le frange con m = 0, 1, 2, . . . si chiamano di ordine zero,
del primo ordine, del secondo ordine e cosi’ via.
Si puo’ anche notare che la distanza tra due massimi di intensita’ successivi e’ sempre la stessa
e vale λD/d. Grazie a questa formula e’ quindi possibile, misurata la distanza tra due frange,
la distanza tra gli schermi D e tra le fenditure d, ottenere la lunghezza d’onda di un’eventuale
lampada di lunghezza d’onda sconosciuta usata come sorgente.
5
1.4
Interferenza da Riflessioni Multiple
Uno degli effetti di interferenza piu’ semplici da realizzare e’ quello che si verifica quando la luce
viene riflessa piu’ volte tra le due superfici di una pellicola trasparente. E’ questo effetto che
provoca i colori nel caso di una sottile pellicola di olio disposta sull’acqua o di una bolla di sapone.
Faremo riferimento nel seguito al caso di una pellicola di materiale trasparente posta a separare
una superficie di vetro dall’aria. E’ un caso che puo’ permettere di schematizzare il trattamento
antiriflesso degli occhiali.
Figura 5: Riflessione da parte di un film trasparente
Consideriamo una luce proveniente da una sorgente puntiforme monocromatica che, partendo dall’aria (na ∼ 1) va a colpire una sottile lamina trasparente di indice di rifrazione nf = 1.38. Al di
sotto del film trasparente sta un vetro ottico (nv = 1.5). Essendo sia il film che il vetro trasparenti
ci possiamo immaginare che i coeficenti di riflessione saranno piccoli. Nel seguito considereremo
solo i primi due raggi riflessi in aria, essendo l’intensita’ dei raggi dovuti alle successive riflessioni
troppo deboli, anche mille volte inferiori alle intensita’ dei primi due raggi, che risultano invece
essere assai simili tra loro, e che possiamo quindi nel seguito considerare uguali. Possiamo quindi
considerare quei due raggi (1 e 2 nella figura 1.4) come provenienti da due sorgenti puntiformi
coerenti.
6
Calcoliamo ora la differenza di cammino ottico per questi due raggi per andare dalla sorgente S
al punto P . La lente L e’ stata messa per far convergere nel punto P il fascio di raggi riflessi.
Puo’ schematizzare la lente del cristallino, nel qual caso il punto P viene a trovarsi sulla retina di
un ipotetica persona che osserva gli occhi di colui che indossa gli occhiali antiriflesso. La presenza
della lente L non comporta alcuna complicazione nel calcolo dell’intensita’ luminosa presente in P .
Esiste infatti un noto teorema dell’ottica geometrica, detto talvolta teorema di Malus, che afferma
che le relazioni di fase in P dei vari raggi sono le stesse di quelle che si hanno prima della lente nei
punti P1 e P2 , intersezione dei raggi con una retta a loro perpendicolare. In pratica, senza scendere
nei dettagli riscontrabili in ogni testo di ottica geometrica, la differenza di cammino compiuta al di
fuori della lente e’ compensata dalla differente lunghezza del percorso all’interno della lente stessa.
Il fatto che i due raggi siano tra loro paralleli e’ un semplice esercizio di ottica geometrica svolto
in appendice.
La differenza di cammino ottico tra questi due raggi risulta quindi essere
∆ = nf (AB + BC) − na (AD)
Ma dalla costruzione geometrica data in figura segue immediatamente che AB = BC = d/ cos θt ,
quindi
2nf d
∆=
− na (AD)
cos θt
A questo punto posso scrivere per la legge di Snell
AD = AC sin θi = AC
nf
sin θt
na
Inoltre AC = 2d tan θt . Ne segue che
∆=
2nf d
(1 − sin2 θt ) = 2nf d cos θt
cos θt
A questo punto abbiamo ricavato la differenza di cammino ottico tra i due raggi, e possiamo ricavare
quindi lo sfasamento tra le due onde. Infatti dalla formula ?? segue che:
δ = k∆ =
4π
nf d cos θt
λ
Grazie alle ipotesi che abbiamo fatto all’inizio sul comportamento dei due raggi possiamo scrivere
l’intensita’ risultante dall’interferenza tra i due raggi allo stesso modo dell’espressione 4. Come
in quel caso avremo quindi interferenza costruttiva tra le due onde se δ = 2mπ e interferenza
distruttiva se δ = (2m + 1)π.Nel caso del trattamento antiriflesso ci interessa il caso di interferenza
distruttiva che equivale alla situazione per cui l’intensita’ della luce riflessa si riduce a 0. Esso
equivale a
4π
nf d cos θt = (2m + 1)π
λ
che nel caso di m = 0 si riduce a
4
nf d cos θt = 1
λ
Se poi consideriamo che la luce incida con un angolo di incidenza vicino allo zero allora possiamo
considerare pari a 1 il termine in coseno e scrivere
4
nf d = 1
λ
7
Da cui segue che lo spessore d del trattamento antiriflesso deve essere
λ
=d
4nf
(6)
Quindi se su una lente si deposita uno spessore d di materiale antiriflesso di indice di rifrazione
minore di quello del vetro la luce riflessa ad incidenza normale viene soppressa quasi completamente
per interferenza. Affinche’ la distruzione sia completa e’ necessario che le ampiezze delle due onde
siano il piu’ possibile uguali, condizione che si realizza se l’ndice di rifrazione del film antiriflesso e’
tale che
√
nf = na nv
(7)
E’ possibile fare alcune considerazioni che ci permettono di spiegare il comportamento delle lenti
antiriflesso. In primo luogo ovviamente, in rispetto del principio di conservazione dell’energia,
l’energia che non viene riflessa non viene distrutta. L’energia che non viene riflessa viene invece
trasmessa, potendo cosi’ giungere sull’occhio della persona che porta gli occhiali. Il vantaggio delle
lenti antiriflesso e’ quindi sia quello di migliore la visione di chi le porta, sia quello di eliminare
antiestetici riflessi. In un primo tempo i rivestimenti venivano fatti depositando diversi strati
monomolecolari di sostanza organica su lastre di vetro. In un secondo tempo e’ stato possibile
realizzarne di piu’ resistenti depositando sulla superficie, per evaporazione sottovuoto, un sottile
strato di fluoruro di magnesio. L’indice di rifrazione del floruro di magnesio e’ n ' 1.38. Tale valore
e’ effettivamente piu’ grande rispetto a quello che sarebbe imposto dalla condizione 7, ma e’ valido
soprattutto se si usano due o piu’ strati sovrapposti.
Osservando la riflessione ad angoli grandi della luce su una lente trattata antiriflesso si nota che la
lente assume una certa colorazione, che nella maggior parte dei casi e’ un rosso porpora. Infatti,
come si vede bene nella formula 6 la condizione di interferenza distruttiva dipende dalla lunghezza
d’onda della radiazione considerata, ed e’ quindi perfettamente soddisfatta per una sola lunghezza
d’onda, che viene di solito scelta verso la meta’ dello spettro visibile. La riflessione della luce rossa
e della luce violetta risulta quindi maggiore, provocando la caratteristica colorazione.
La dipendenza dalla lunghezza d’onda provoca anche la caratteristica colorazione delle bolle di
sapone.
Allo stesso modo abbiamo visto che la 6 e’ valida quando l’angolo di incidenza e’ molto piccolo.
Infatti la differenza tra un vetro trattato e uno non trattato diminuisce con l’aumentare dell’angolo
di riflessione, e il comportamento antiriflesso e’ molto migliore per angoli piccoli (vedi fig.1.4).
8
Figura 6: Riflettanza pencentuale di un vetro trattato e di un vetro non trattato (uncoated): é
evidente il miglioramento dovuto al trattamento
Figura 7: Rfilettanza di un vetro trattato visto a 0 e 45 gradi
9
Figura 8: Riflessione da parte di un vetro trattato con un trattamento multistrato
10