Progetto LES
Sceneggiatura Circuiti 3 ver.
sett..2002
Circuiti resistivi in serie e in parallelo
Nella fase iniziale si discuterà sulle conclusioni a cui si era giunti nelle attività precedenti. La prima
esperienza di questa attività riguarderà un approfondimento relativo alla lampadina, prima si
realizzerà la curva caratteristica evidenziando la non linearità poi, nei casi in cui è possibile, si
lavorerà per determinare la costante di Stefan-Boltzmann. Si realizzeranno circuiti con portatori di
carica diversi e poi si lavorerà con semplici reti al fine di evidenziare i principi di conservazione
della carica e dell'energia. Il legame con i fenomeni quotidiani riguarderà l’impianto elettrico di
casa, cosa accade quando si prende una scossa elettrica, i consumi e la possibilità di utilizzare gli
effetti magnetici della corrente
La curva corrente-tensione di una lampadina
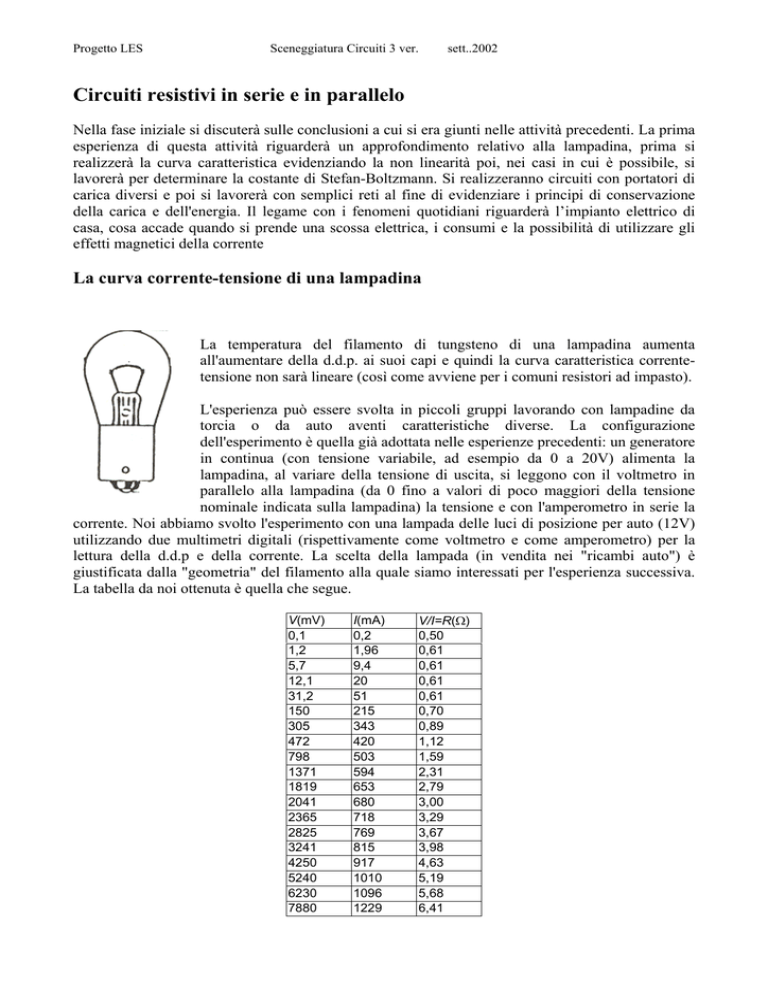
La temperatura del filamento di tungsteno di una lampadina aumenta
all'aumentare della d.d.p. ai suoi capi e quindi la curva caratteristica correntetensione non sarà lineare (così come avviene per i comuni resistori ad impasto).
L'esperienza può essere svolta in piccoli gruppi lavorando con lampadine da
torcia o da auto aventi caratteristiche diverse. La configurazione
dell'esperimento è quella già adottata nelle esperienze precedenti: un generatore
in continua (con tensione variabile, ad esempio da 0 a 20V) alimenta la
lampadina, al variare della tensione di uscita, si leggono con il voltmetro in
parallelo alla lampadina (da 0 fino a valori di poco maggiori della tensione
nominale indicata sulla lampadina) la tensione e con l'amperometro in serie la
corrente. Noi abbiamo svolto l'esperimento con una lampada delle luci di posizione per auto (12V)
utilizzando due multimetri digitali (rispettivamente come voltmetro e come amperometro) per la
lettura della d.d.p e della corrente. La scelta della lampada (in vendita nei "ricambi auto") è
giustificata dalla "geometria" del filamento alla quale siamo interessati per l'esperienza successiva.
La tabella da noi ottenuta è quella che segue.
V(mV)
0,1
1,2
5,7
12,1
31,2
150
305
472
798
1371
1819
2041
2365
2825
3241
4250
5240
6230
7880
I(mA)
0,2
1,96
9,4
20
51
215
343
420
503
594
653
680
718
769
815
917
1010
1096
1229
V/I=R(Ω)
0,50
0,61
0,61
0,61
0,61
0,70
0,89
1,12
1,59
2,31
2,79
3,00
3,29
3,67
3,98
4,63
5,19
5,68
6,41
Progetto LES
Sceneggiatura Circuiti 3 ver.
9010
10016
11190
11800
12740
14180
15260
16090
16990
17580
18240
18630
1314
1396
1467
1507
1568
1659
1724
1774
1828
1864
1902
1926
sett..2002
6,86
7,17
7,63
7,83
8,13
8,55
8,85
9,07
9,29
9,43
9,59
9,67
Tabella Excel con i dati dell'esperimento
Nella prima colonna sono riportati i valori della d.d.p. Come si vede abbiamo superato il valore
nominale della lampada (senza provocarne la rottura). All'aumentare della tensione aumenta anche
la corrente (seconda colonna) e quindi aumenta anche la potenza dissipata VI, ma il rapporto non
resta costante (ultima colonna). Come si vede rispetto al valore iniziale (0,5 Ω a temperatura
ambiente) la resistenza diventa alla fine (circa 18 V e 1,9A ) pari a circa venti volte il valore iniziale
(10 Ω).
2000
1800
2
y = -2E-06x + 0,1159x + 436,82
1600
2
R = 0,998
I (mA)
1400
1200
1000
800
600
400
200
0
0
5000
10000
15000
20000
V (mV)
Grafico Excel con i dati della tabella precedente
Il grafico è stato realizzato escludendo i dati delle prime sei righe (dati che servono a determinare la
resistenza a temperatura ambiente per l'esperimento successivo). Il grafico mostra la non linearità
della relazione corrente-tensione con i dati sperimentali che sono ben rappresentati da una parabola
dei minimi quadrati così come mostrato dal valore prossimo a 1 dell'indice di correlazione.
La temperatura del filamento
Le lampada e utilizzate hanno il filamento in tungsteno. Il tungsteno (Wolframio) elemento
metallico di simbolo W e numero atomico 74, appartiene agli elementi di transizione della tavola
periodica, ed è l'elemento con il più alto punto di fusione. Fonde a 3410 °C e bolle a circa 5927 °C.
Sulle proprietà del tungsteno possono essere svolte ricerche in rete di interesse per la chimica e la
fisica. Le ricerche con un motore con "Tungesteno" o "Tungsten" danno molti risultati, si veda ad
esempio:
http://www.tungsten.com/mtstung.html;
Progetto LES
Temperatura
K
300
400
500
600
700
800
900
1000
1100
1200
1300
1400
1500
1600
1700
1800
1900
2000
Sceneggiatura Circuiti 3 ver.
Resistività
Ωm
5,65E-08
8,06E-08
1,06E-07
1,32E-07
1,61E-07
1,9E-07
2,19E-07
2,49E-07
2,79E-07
3,1E-07
3,41E-07
3,72E-07
4,04E-07
4,36E-07
4,68E-07
5,01E-07
5,34E-07
5,67E-07
Temperatura
K
2100
2200
2300
2400
2500
2600
2700
2800
2900
3000
3100
3200
3300
3400
3500
3600
3655
sett..2002
Resistività
Ωm
6,01E-07
6,35E-07
6,69E-07
7,04E-07
7,39E-07
7,75E-07
8,1E-07
8,47E-07
8,83E-07
9,2E-07
9,58E-07
9,95E-07
1,03E-06
1,07E-06
1,11E-06
1,15E-06
1,17E-06
Tabella CRC-Handbook of Physics and Chemistry 10-283
Nella tabella sono riportati valori della resistività in funzione della temperatura
1,E-06
4000
3500
1,E-06
y = 6E-11x
tem peratura (K)
resistività (Wm)
3000
8,E-07
1,205
2
R = 0,9999
6,E-07
4,E-07
2500
2000
y = 3E+08x 0,8298
R2 = 0,9999
1500
1000
2,E-07
500
0,E+00
0
500
1000
1500
2000
2500
3000
3500
4000
temperatura (K)
0
0,E+00
2,E-07
4,E-07
6,E-07
8,E-07
1,E-06
resistività ( Ω m )
Grafici Excel con i dati della tabella precedente
Il grafico a sinistra rappresenta la resistività in funzione della temperatura quello a destra la
temperatura in funzione della resistività. Anche se la relazione lineare può essere adoperata senza
grossi errori per la sua semplicità, la ricerca con le curve dei minimi quadrati mostra che con la
funzione potenza è possibile calcolare con grande accuratezza (indice di correlazione pari a 1) la
resistività (e la resistenza) nota la temperatura oppure la temperatura se è nota la resistività
(resistenza).Le relazioni sono rispettivamente
R= Rin (T/Tin)γ
T= Tin (R/Rin)1/γ
con γ =1,205 e quindi 1/γ=0,8298
Tin,Rin rispettivamente temperatura e relativa resistività iniziali (a temperatura ambiente)
1,E-06
Progetto LES
Sceneggiatura Circuiti 3 ver.
sett..2002
Le due equazioni sono di grande interesse anche perché sperimentalmente è facile misurare il
rapporto tra resistenze pari al rapporto tra resistività se non cambia la geometria del conduttore.
Misura della costante di Stefan-Boltzmann
Il filamento della lampadina emette radiazione elettromagnetica. La potenza di emissione dipende
dalla quarta potenza della temperatura assoluta del corpo (filamento) secondo la legge di StefanBoltzmann
P=e σAT 4 (in watt)
con
e =emissività della superficie, compresa tra 0 e 1 (corpo nero perfetto);
σ =costante di Stefan-Boltzmann pari a circa 5,7 10-8 W/m2K4
A= area della superficie emittente;
T= temperatura assoluta espressa in gradi Kelvin
Adoperando gli stessi dati (V,I con i quali è stata determinata la curva caratteristica) per calcolare la
potenza e la resistenza e nota la dipendenza della temperatura dalla resistività è possibile
determinare σ.
La procedura è sinteticamente la seguente:
• si misurano temperatura e resistenza iniziale
• si misurano le dimensioni del filamento della lampadina
• si calcolano la potenza e la temperatura
• si determina la costante di proporzionalità esistente tra P e T4.
Noi abbiamo fissato la temperatura ambiente a 300K e determinata la resistenza a temperatura
ambiente come rapporto V/I per valori piccolissimi di V (e I) quindi 0,5Ω (vedi tabella
esperimento). Per la misura del filamento abbiamo rotto la lampada e misurato con il calibro il
diametro pari a 0,45mm e la lunghezza pari a 7 mm. Con questi valori si ottiene A circa pari a 9,9
mm2= 9,9 10-6 m2
Le elaborazioni effettuate con tabelle excel sono commentate nel seguito.
V(mV)
0,1
1,2
5,7
12,1
31,2
150
305
472
798
1371
1819
2041
2365
2825
3241
4250
5240
6230
7880
9010
10016
11190
11800
I (mA)
0,2
1,96
9,4
20
51
215
343
420
503
594
653
680
718
769
815
917
1010
1096
1229
1314
1396
1467
1507
P (watt)
2,0E-08
2,4E-06
5,4E-05
2,4E-04
1,6E-03
3,2E-02
1,0E-01
2,0E-01
4,0E-01
8,1E-01
1,2E+00
1,4E+00
1,7E+00
2,2E+00
2,6E+00
3,9E+00
5,3E+00
6,8E+00
9,7E+00
1,2E+01
1,4E+01
1,6E+01
1,8E+01
R(Ω)
0,50
0,61
0,61
0,61
0,61
0,70
0,89
1,12
1,59
2,31
2,79
3,00
3,29
3,67
3,98
4,63
5,19
5,68
6,41
6,86
7,17
7,63
7,83
R/R0
1,00
1,22
1,21
1,21
1,22
1,40
1,78
2,25
3,17
4,62
5,57
6,00
6,59
7,35
7,95
9,27
10,38
11,37
12,82
13,71
14,35
15,26
15,66
T (K)
300
355
352
351
355
396
484
587
782
1067
1248
1327
1434
1570
1676
1904
2090
2255
2492
2635
2736
2878
2941
T4 (K)4
8,1E+09
1,6E+10
1,5E+10
1,5E+10
1,6E+10
2,4E+10
5,5E+10
1,2E+11
3,7E+11
1,3E+12
2,4E+12
3,1E+12
4,2E+12
6,1E+12
7,9E+12
1,3E+13
1,9E+13
2,6E+13
3,9E+13
4,8E+13
5,6E+13
6,9E+13
7,5E+13
Progetto LES
12740
14180
15260
16090
16990
17580
18240
18630
Sceneggiatura Circuiti 3 ver.
1568
1659
1724
1774
1828
1864
1902
1926
2,0E+01
2,4E+01
2,6E+01
2,9E+01
3,1E+01
3,3E+01
3,5E+01
3,6E+01
8,13
8,55
8,85
9,07
9,29
9,43
9,59
9,67
16,25
17,09
17,70
18,14
18,59
18,86
19,18
19,35
sett..2002
3033
3163
3256
3323
3391
3433
3480
3505
8,5E+13
1,0E+14
1,1E+14
1,2E+14
1,3E+14
1,4E+14
1,5E+14
1,5E+14
Tabella Excel con le elaborazioni dei dati dell'esperimento precedente
La prima, la seconda e la quarta colonna sono quelle della tabella precedente. Nella quinta colonna
è calcolato il rapporto tra la resistenza corrente e quella iniziale (a temperatura ambiente): tale
rapporto è anche pari al rapporto tra le resistività e consente il calcolo della temperatura (sesta
colonna) con la relazione sperimentale ricavata precedentemente con il fit con Excel. La relazione
che interessa è ovviamente quella tra i valori di P e T4 .
4,0E+01
3,5E+01
y = 2,3E-13x
2
R = 0,9982
3,0E+01
P( W)
2,5E+01
2,0E+01
1,5E+01
1,0E+01
5,0E+00
0,0E+00
0,0E+00
5,0E+13
1,0E+14
T
4
(K)
1,5E+14
4
Grafico Excel
La diretta proporzionalità tra P e T4 (il grafico si riferisce ai valori evidenziati relativi ad una
temperatura maggiore di 1000K per cui prevale l'irraggiamento) è evidenziata dalla bontà
dell'interpolazione lineare (coefficiente di correlazione circa pari a 1). La pendenza della retta è pari
a eσA=2,3 10-13 W/K4(P=eσAT 4 ). Assumendo per il tungsteno e=0,5 e avendo misurato A=9,9
10-6 m2 si ha σ=4,6 W/m2K4
Progetto LES
Sceneggiatura Circuiti 3 ver.
sett..2002
I portatori di carica
La conduzione non avviene sempre con gli stessi portatori di carica. Per i metalli la conduzione è
dovuto al moto degli elettroni liberi di migrare all'interno del metallo, ma legati ad esso nel suo
insieme.
Per i liquidi, invece, sono da considerarsi buoni conduttori quelli che contengono ioni. In questo
caso i portatori di carica sono atomi o molecole con una deficienza o un eccesso di elettroni. Se
analizziamo la soluzione di cloruro di sodio che abbiamo realizzato, cioè il sale da cucina disciolto
in acqua, questa presenta ioni Na+ e Cl- che sono i portatori di carica per questa soluzione. L'acqua
ordinaria (quella della fontana), al contrario di quella distillata, è un buon conduttore perché le
impurità disciolte al suo interno forniscono gli ioni che presiedono alla conduzione.
Si può accennare alla conduzione nei gas che avviene solo quando questi sono stati ionizzati
richiamando alla memoria dei ragazzi le lampade al neon normalmente utilizzate per illuminare le
uffici e abitazioni. In un gas ionizzato la conduzione, anche se sono presenti sia ioni che elettroni
liberi, è dovuta principalmente al moto di questi ultimi.
Nella tabella seguente sono riportate delle misure di tensione e intensità di corrente effettuate in un
circuito, alimentato da un generatore in continua ad una tensione di 10V, formato da conduttori
metallici e non.
Tensione di
alimentazione
10 V
Portatori di
carica
Elemento circuitale
Caduta di potenziale
(V)
Intensità di corrente
(mA)
Resitenza
(Ω)
Ioni
Ioni
Ioni
Elettroni
Mela
Arancia
Acqua + Sale
Resistore (1000 Ω)
4,6
4,0
0,33
0,44
0,5
"
"
"
9200
8000
660
880
Il verso della corrente
"Il LED è un dispositivo realizzato ponendo a contatto due semiconduttori, uno drogato di tipo p
l'altro drogato di tipo n. Tale giunzione p-n permette il passaggio di corrente solo dalla regione p
alla regione n e non il viceversa evidenziando così il verso della corrente.
La pila pompa un flusso costante di elettroni nella regione n asportando elettroni nella regione p.
Gli elettroni e le lacune si incontrano nell'interfaccia dove si annichilano, processo che può
continuare indefinitivamente.
Progetto LES
Sceneggiatura Circuiti 3 ver.
sett..2002
Se invece la regione p viene collegata al polo negativo della pila e la regione n al polo positivo, la
giunzione si dice polarizzata inversamente.
Le lacune libere nella regione p defluiscono verso il polo negativo della pila senza attraversare la
giunzione, mentre gli elettroni liberi della regione n vanno verso il polo positivo, sempre senza
attraversare la giunzione. In polarizzazione inversa la corrente termina quasi immediatamente
perché si svuotano le due regioni dei portatori di carica."1
Spunti per un'attività di laboratorio
Curva caratteristica di un diodo.
Il campo elettrico presente nell'interfaccia tra le due giunzioni di un diodo tende ad essere annullato
dal campo elettrico dovuto alla sorgente di f.e.m. applicata. Al crescere della tensione applicata ai
capi del diodo cresce quindi l'intensità di corrente che l'attraversa perché il processo di
annichilazione degli elettroni e delle lacune nell'interfaccia è facilitato. La crescita, però,
dell'intensità di corrente non è direttamente proporzionale all'aumento della tensione applicata.
La curva caratteristica di un diodo, utilizzato in polarizzazione diretta, mostra come la giunzione pn non obbedisce alla legge di Ohm.
Spunti per un'attività di laboratorio
Andamento del campo magnetico generato da un filo rettilineo percorso da corrente elettrica.
Facciamo passare corrente in un filo rettilineo. Utilizzando il campo magnetico locale ritroveremo
sperimentalmente che il campo magnetico prodotto dalla corrente che circola nel filo è direttamente
proporzionale all'intensità della corrente che lo attraversa ed inversamente proporzionale alla
distanza dal filo.
Per effettuare questo esperienza è necessario un filo elettrico lungo almeno 1 metro, un generatore
in corrente continua che eroghi una corrente di intensità pari a qualche ampere, due supporti a
colonna, una bussola con il quadrante suddiviso in gradi, un tester ed un riga.
Ponendo la bussola su di un piano e il filo, nella direzione N-S, sui due supporti si osserva una
deviazione dell'ago magnetico quando il filo viene percorso da corrente elettrica.
Il filo percorso da corrente genera un campo magnetico Bf che si somma vettorialmente al campo
magnetico locale Bl, quest'ultimo risultante dal campo magnetico terrestre sommato a quello
eventualmente prodotto da tutto il materiale ferroso, da altri fili percorsi da corrente, ecc. posto
nelle vicinanze della bussola.
Per l'individuazione dell'andamento del campo magnetico prodotto dal filo ci serviamo della
seguente costruzione geometrica. Si disegna un segmento OB e una retta AB perpendicolare ad
esso. Se l'ago della bussola devia di un angolo α, a partire da O è possibile tracciare un segmento
OC, che formi un angolo α con OB, il quale individua sulla retta AB un segmento BC
proporzionale all'intensità del campo magnetico prodotto dal filo. Vale la proporzione seguente:
1
"Fisica" H. C. Ohanian, Zanichelli editore.
Progetto LES
Sceneggiatura Circuiti 3 ver.
sett..2002
Β f BC
=
B l OB
L'intensità del campo magnetico locale non è nota ma ritrovandola in tutte le misure possiamo dire
che l'intensità del campo magnetico prodotto dal filo percorso da corrente è nota a meno di una
costante pari a Bl.
Possiamo, quindi, effettuare le misure annotando la deviazione dell'ago della bussola ad ogni valore
della corrente erogata I ed, a parità di corrente, a diverse distanze del filo dalla bussola. Annotando
su di una tabella le diverse misure effettuate, ed in particolare il rapporto BC /I e il prodotto BC ⋅α,
si osserva che queste due ultime quantità sono costanti entro gli errori sperimentali.
Abbiamo così ritrovato l'induzione magnetica di un filo conduttore rettilineo.
Quindi il verso con cui la corrente si muove lungo un circuito è determinato dalla disposizione dei
poli della pila che, lungo il circuito, sospinge elettroni dal suo polo negativo verso quello positivo,
mentre dentro la pila risucchia elettroni dal polo positivo e li sospinge verso quello negativo.
Utilizziamo questo modello di funzionamento della pila per meglio comprendere il comportamento
di più pile poste in serie. Nel collegamento corrispondente allo schema 1° e 4° le quattro pile
spingono gli elettroni lungo il circuito in modo concorde; l'insieme delle quattro pile è, quindi,
equivalente ad una pila di tensione pari alla somma delle tensioni. Nel collegamento 2° e 3°, le
quattro pile spingono gli elettroni in modo discorde, cioè l'azione di una è ostacolata da quella di
un'altra, l'insieme delle quattro pile è equivalente ad una pila di tensione pari alla somma algebrica
delle tensioni fornite dalle singole pile.
Progetto LES
Sceneggiatura Circuiti 3 ver.
sett..2002
I diversi esperimenti realizzati in questa fase dell'AD hanno messo in luce che la corrente ha un
verso di percorrenza. Questo verso della corrente, in relazione alla polarità della pila, in alcuni
utilizzatori non è riscontrabile (vedi lampadina), in altri causa un diverso comportamento (vedi
motorino con ventola che cambia il verso di rotazione da orario ad antiorario e/o viceversa), oppure
non ne permette il funzionamento (vedi Led che alimentato in polarizzazione inversa non emette
luce).
Resistenze in serie e in parallelo
Le esperienze fino ad ora realizzate hanno messo in evidenza come due utilizzatori in parallelo
offrono due strade indipendenti con una corrente che attraversa l'alimentatore che è pari alla somma
delle correnti che passano nei due utilizzatori, mentre per i due utilizzatori posti in serie la corrente
che percorre entrambi è minore di quella che si avrebbe se la pila fosse collegata ad una singolo
utilizzatore.
Attraverso misure di intensità di corrente e di tensione, ricaviamo il valore numerico della
resistenza totale offerta dal serie e dal parallelo delle resistenze fornite: R1 = 100 Ω e R2 = 330 Ω.
Se analizziamo il comportamento di due resistenze in serie la corrente che li attraversa ha la stessa
intensità, applicando la legge di Ohm ad entrambi i conduttori, e vista l'uguaglianza tra le due
intensità di corrente, è possibile ricavare il valore della resistenza equivalente.
V = R1 ⋅ I
⇒
V = R2 ⋅ I
V
= ( R1 + R2 )
I
Si perviene, entro gli errori sperimentali, allo stesso risultato effettuando delle misure di tensione ed
intensità di corrente
I [A]
(19 ± 1) ⋅ 10-3
V [V]
8,0 ± 0,2
420
V
[V / A]
I
poiché facendo il rapporto tra le due misure si ottiene la resistenza equivalente.
Per il calcolo, invece, della resistenza equivalente di due resistenze poste in parallelo, poiché ai loro
capi tensione è la stessa, per la legge dei nodi la corrente I che circola nel parallelo è somma delle
due correnti che circolano nei due rami. Applicando la legge di Ohm ad entrambi i conduttori e
sommando membro a membro le due relazioni si ricava la resistenza equivalente.
I1 =
V
R1
⇒
I2 =
V
R2
1
1
I = I 1 + I 2 = V +
R1 R2
Si perviene, entro gli errori sperimentali, allo stesso risultato effettuando delle misure di tensione ed
intensità di corrente
Progetto LES
Sceneggiatura Circuiti 3 ver.
sett..2002
I [A]
(100 ± 10) ⋅ 10-3
V [V]
8,0 ± 0,2
80
V
[V / A]
I
Calcolando il rapporto tra le due misure effettuate si ottiene la resistenza equivalente alle due
resistenze poste in parallelo il cui inverso risulta essere proprio uguale alla somma degli inversi.
Abbiamo con queste misure calcolato il valore numerico della resistenza totale. Si possono quindi
fare dei richiami a fenomeni già osservati.
Come si ripartisce la corrente
Come si comporta la corrente quando entra in un nodo? Senza voler giungere alla formulazione
matematica delle due leggi di Kirchoff sui nodi2 e sulle maglie3 poniamo attenzione al ponte
riportato di seguito, formulando, in prima istanza, delle ipotesi sul serie o sul parallelo degli
elementi presenti.
SERIE O
PARALLELO?
R2
R5+ R6
R5
SPIEGA.
Serie
R3
Le resistenze sono in serie perché
percorse dalla stessa corrente.
Parallelo
R4
Serie
R6
Le resistenze sono in parallelo
perché percorse da corrente di
diversa intensità.
Le resistenze sono in serie perché
percorse dalla stessa corrente.
Una volta costruito il circuito con le resistenze a disposizione si verificano le ipotesi fatte, attraverso
misure eseguite con il tester di intensità di corrente e tensione.
R1
25 Ω
R2
50 Ω
R3
150 Ω
R4
40 Ω
R5
50 Ω
R6
50 Ω
SERIE O PARALLELO? SPIEGA.
V2= 3,0 V
I2= 62 mA
Le resistenze sono in serie perché percorse
dalla stessa corrente mentre ai loro capi la
caduta di tensione è diversa
V5+6= 13 V V4= 13 V
Le resistenze sono in parallelo perché percorse
I4= 130 mA I3= 320 mA da corrente di diversa intensità mentre ai loro
capi la caduta di tensione è la stessa
V5= 6,2 V
V6= 6,4 V
Le resistenze sono in serie perché percorse
I4= 130 mA I4= 130 mA dalla stessa corrente, con ai loro capi la stessa
caduta di tensione.
2
V3= 9,4 V
I2= 62 mA
Il primo principio di Kirchoff, anche detto principio dei nodi, afferma che "la somma delle intensità di tutte le correnti
che entrano in un qualsiasi nodo del circuito deve essere uguale alla somma delle correnti che escono dal nodo:
Σn In (t)=0". Questo principio esprime la conservazione della carica elettrica, ossia nell'unità di tempo la quantità di
carica che entra in un nodo è pari a quanta ne esce.
3
Il secondo principio di Kirchoff , anche detto principio delle maglie, stabilisce che "lungo qualsiasi maglia la somma
algebrica di tutte le variazioni di potenziale deve essere nulla: Σn Vn (t)=0". Questo principio esprime la conservazione
dell'energia quando nella maglia analizzata non è presente nessun elemento dissipatore o accumulatore.
Progetto LES
Sceneggiatura Circuiti 3 ver.
sett..2002
In particolare il ramo del ponte, formato da R5 e R6, ha le due resistenze che non solo sono percorse
dalla stessa corrente ma che inoltre, anche se in serie, presentano la stessa caduta di tensione (entro
gli errori sperimentali) ai loro capi. L'aver utilizzato in questo ramo due resistenze uguali poste in
serie serve a sottolineare che non basta affermare che uguale tensione indica due resistenze in
parallelo, mentre uguale corrente individua due resistenze in serie, perché nel caso delle resistenze
R5 e R6 esse sono, contemporaneamente, percorse dalla stessa corrente e presentano ai loro capi la
stessa caduta di tensione. E' necessario, quindi, individuare un'altra regola che permetta la corretta
classificazione. Per elementi in serie la corrente è la stessa in ogni punto, mentre la caduta di
tensione ai capi di questa serie è pari alla somma algebrica delle singole cadute di tensione. Per
elementi in parallelo la caduta di tensione è la stessa per ogni elemento mentre la corrente entrante
nel parallelo è uguale a quella uscente ed è pari alla somma delle correnti che percorrono i diversi
rami del parallelo.
Definendo, quindi, il nodo come il punto dove convergono diversi fili conduttori, si misura la
corrente che attraversa le seguenti resistenze riportando i valori ottenuti nella tabella preceduti dal
segno (+) se la corrente è entrante nel nodo, meno (-) se è uscente.
I [A]
I1
+ 0,490
I2
- 0,062
I3
- 0,320
I4
- 0,130
Analizzando i dati riportati in tabella si osserva che la somma algebrica delle intensità delle correnti
che entrano e/o escono dal nodo è zero, entro gli errori sperimentali.
Continuando nell'analisi del ponte realizzato spostiamo la nostra attenzione sulle cadute di tensione
ai capi delle diverse resistenze. Nella maglia, riportata in figura, si eseguono delle misure di
tensione ai capi dei resistori R2 ,R3 e R4. Si fissa un verso di percorrenza all'interno della maglia e si
attribuisce il segno positivo (+) alla tensione misurata se in modo concorde con il verso fissato, c'è
caduta di tensione, negativo (-) nell'altro caso. Si riportano i valori misurati nell'apposita tabella.
V[V]
V2
3,0
V3
9,4
V4
- 13
Da una rapida analisi dei dati ottenuti ancora una volta si vede che la somma algebrica delle cadute
di tensione dà risultato zero.
Ma come comportarsi e cosa ci si aspetta se all'interno della maglia non ci sono solo elementi
lineari4 passivi5? Nella maglia, riportata nella figura seguente, sono presenti tre elementi passivi, le
4
Un elemento è lineare quando tra la differenza di potenziale ai suoi capi e la corrente che lo attraversa esiste una
relazione funzionale del tipo I(t)=O[V(t)], con O operatore lineare. Un operatore O è una funzione matematica che può
essere eseguita su di una funzione f(t) trasformandola in un'altra funzione g(t). Un operatore è poi lineare se:
a) O[f(t) + g(t)] = O[f(t)] + O[g(t)]
b) O[Kf(t)] =KO[f(t)]
Ad esempio sono operatori lineari la moltiplicazione per una costante, la derivazione, l'integrazione. Non sono lineari la
radice, il logaritmo.
Progetto LES
Sceneggiatura Circuiti 3 ver.
sett..2002
resistenze, ed un elemento attivo, il generatore. Si eseguono delle misure di tensione ai capi dei
resistori R1, R2 e R3 e si controlla il valore della tensione erogata dal generatore.
V[V]
V1
12
V2
3,0
V3
9,4
Pila
- 25
Dall'osservazione dei dati riportati in tabella nuovamente si ha che la somma algebrica dei valori
misurati dà zero, purché nel calcolo si tenga conto anche della tensione erogata dal generatore.
Gli effetti della corrente
E' visibile la corrente elettrica quando scorre in un conduttore? Non c'è niente di osservabile che si
muove lungo il conduttore ma è solo, ad esempio, l'accendersi di una lampadina che ne rivela il
passaggio. E', quindi, possibile accorgersi di tale flusso perché crea degli effetti rilevabili; ma quali
sono questi effetti?
L'effetto termico, o effetto Joule, è sicuramente il primo suggerito dai ragazzi. Il filamento di
tungsteno portato all'incandescenza si riscalda ed emette luce, l'avvolgimento di una stufa elettrica
si scalda fino a diventare incandescente, il ferro da stiro si riscalda: l'energia elettrica si può
trasformare in energia termica.
Si riprende in esame il semplice circuito resistivo pila-lampadina e si osserva che il filamento di
tungsteno cambia colore, mentre sta andando all'incandescenza, passando dal rosso al bianco.
Osservazione fortemente influenzata dall'illuminazione ambientale.
Spunti per un approfondimento
La lampadina ad incandescenza.
Il filamento di tungsteno è l'elemento più importante della lampada: da esso dipendono, in
particolare, la qualità e la quantità della luce e la luce emessa.
La qualità della luce dipende essenzialmente dalla sua tonalità e dall'indice di resa cromatica. La
tonalità di luce emessa da una lampada è caratterizzata dalla temperatura di colore, espressa in gradi
Kelvin (K). Bassi valori della temperatura di colore corrispondono a tonalità calde e viceversa alti
valori corrispondono a tonalità fredde. Ad esempio una luce bianca calda per interni si aggira sui
2700 K (lampada ad incandescenza) e una luce bianca per grandi magazzini si aggira sui 4000 K.
La luce diurna supera i 5000 K.
Un oggetto, che non emette luce propria, appare di un certo colore perché riflette quelle determinate
lunghezze d'onda. Risulta ovvio che tali lunghezze devono essere presenti nell'emissione della
lampada per essere riflesse. In una buona illuminazione devono essere presenti tutte le lunghezze
5
Un elemento è detto passivo se dissipa una parte dell'energia fornita in calore, oppure l'immagazzina sotto forma di
energia elettrica o magnetica.
Progetto LES
Sceneggiatura Circuiti 3 ver.
sett..2002
d'onda visibili. Quindi l'indice di resa cromatica definisce in che misura la luce emessa da una
sorgente luminosa consente di apprezzare le sfumature di colore degli oggetti illuminati. Al
riguardo le lampade vengono classificate con un indice numerico compreso tra 0 e 100: quanto più
tale indice si avvicina a 100 tanto più la sorgente luminosa consente l'apprezzamento delle
sfumature di colore.
Gli elettroni di conduzione trasferiscono al conduttore, quando urtano contro gli atomi del reticolo,
l'energia elettrica che la pila fornisce loro nell'intervallo di tempo che intercorre tra un urto e il
successivo. L'energia fornita si trasforma completamente in calore dando vita ad un fenomeno
chiamato effetto Joule. Questa energia che si è trasforma in calore può essere facilmente calcolata
utilizzando la conservatività del campo elettrico. La potenza (energia per unità di tempo) dissipata P
è pari a:
P = (∆V) ⋅ I
dove I è la corrente che attraversa il resistore e ∆V è la caduta di potenziale ai capi del resistore.
Dalla legge di Ohm (V=R⋅I) si ottengono tutte le possibili formulazioni della legge di Joule:
P = (∆V) ⋅ I = R⋅I2 = I2 / R
Una delle più importanti applicazioni del riscaldamento prodotto dal passaggio di corrente elettrica
è l'illuminazione elettrica per mezzo delle lampade ad incandescenza. Il passaggio della corrente
elettrica produce un riscaldamento molto forte del filamento della lampadina e lo porta ad un
temperatura molto elevata (2700 K); il filamento diventa allora incandescente ed emette luce.
L'effetto magnetico della corrente è stato già introdotto durante l'osservazione della deviazione
dell'ago di una bussola posta nelle vicinanze di un filo percorso da corrente e nella discussione sul
comportamento della bobina in un tester.
Richiamo storico
Il grande onore della scoperta della connessione tra l'elettricità e il magnetismo toccò al fisico
danese Hans Christian Oersted .. che in un giorno del lontano 1820 .. nell'aula stipata di giovani
studenti posò sul tavolo la sua pila voltaica, ne collegò i poli con un filo di platino e avvicinò ad
essa un ago magnetico: questo, che avrebbe dovuto orientarsi nella direzione Nord-Sud, fece invece
un mezzo giro su se stesso e si fermò in direzione perpendicolare a quella del filo. Il pubblico degli
uditori non fu molto sorpreso, ma Oersted, dopo la lezione si fermò nell'aula con la speranza di
individuare l'origine dell'insolito fenomeno.
Dapprima egli pensò che il moto dell'ago fosse dovuto alle correnti d'aria prodotte dal filo riscaldato
per il passaggio della corrente e, per confermare questa sua supposizione, egli interpose tra l'ago e il
filo di platino un pezzo di cartone con l'intenzione di arrestare le eventuali correnti d'aria, ma non
notò alcuna differenza. Allora ruotò la pila di 180°, invertendo le polarità, in modo da far fluire la
corrente in direzione opposta nel filo do platino, ma anche l'ago ruotò di 180° e il polo Nord si
orientò nella direzione in cui prima era orientato il polo Sud: era evidente che doveva esserci
un'interazione tra i magneti e le cariche elettriche in movimento e che la direzione nella quale la
corrente elettrica fluiva nel filo influenzava l'orientamento dell'ago magnetico.6
6
Biografia della Fisica G. Gamov Edizioni Scientifiche e Tecniche Mondadori
Progetto LES
Sceneggiatura Circuiti 3 ver.
sett..2002
Analizziamo l'effetto magnetico osservando l'interazione tra un magnete ed una bobina percorsa da
corrente.
Ad un sostegno si aggancia un dinamometro al quale è sospeso un magnete in parte immerso in una
bobina. Il dinamometro indica il peso del magnete; se alimentiamo la bobina si osserva che il
magnete viene attratto all'interno della bobina con una conseguente variazione di peso esplicitata
dal dinamometro. E' quindi possibile risalire all'intensità della forza esercitata sulla calamita dal
campo magnetico, generato dalla bobina percorsa da corrente, facendo la differenza tra le due
pesate. L'intensità della forza esercitata varia al variare dell'intensità di corrente che percorre la
spira, dal numero di avvolgimenti, dalla sua sezione e lunghezza. Per evidenziare la dipendenza
dell'intensità del campo magnetico generato dalle ultime tre variabili menzionate è consigliabile
realizzare delle bobine artigianali avvolgendo un filo conduttore intorno ad un cilindro di materiale
non conduttore, ad esempio cartone.
Gli impianti elettrici
Ma perché le centrali elettriche erogano corrente alternata? Perché viene preferita alla continua?
Per minimizzare le perdite per effetto Joule conviene che la corrente viaggi lunga la linea elettrica
ad alta tensione, e con la corrente alternata, con i trasformatori, è più semplice elevare e/o abbassare
il valore della tensione.
Infatti data la resistività λ della linea di trasmissione e la sua lunghezza l, la potenza Pd dissipata
lungo la linea, a parità di potenza erogata Pc dalla centrale, è tanto minore quanto maggiore è la
tensione V di alimentazione della linea stessa. Si ha infatti, supponendo che tutte le impedenze siano
puramente resistive:
Pc = V ⋅ I
Pd = ∆V ⋅ I = (I)2 ⋅ λ ⋅ l
Dove ∆Veff è l caduta di tensione tra i due elementi della linea. Facendo il rapporto membro a
membro si ha la perdita percentuale della linea:
Pd / Pc = (I ⋅λ ⋅ l) / V
Che è tanto minore quanto maggiore è la tensione di alimentazione e quanto minore è la corrente
che attraversa la linea.
Calcoliamo la potenza erogata dalla centrale elettrica secondo la legge di Joule su di un carico
puramente resistivo:
Pd = V2 / R
Se la tensione erogata dalla centrale elettrica è alternata essa è descritta da un'espressione del tipo:
V = Vmax sin ωt
Progetto LES
Sceneggiatura Circuiti 3 ver.
sett..2002
Quindi la potenza dissipata varia al variare di t, ed è necessario calcolare il valor medio di questa
potenza mediando sin2 ωt su di un periodo:
V
(Vmax )2 (Veff )2
Pd =
=
con Veff = max
2R
R
2
dove Veff , detta tensione efficace, è la tensione quadratica media.
I 220 V della tensione di rete è il valore efficace della tensione erogata all'utente che ha il valore
Vmax pari a 311 V.
Risulta così chiaro che la potenza alternata media dissipata nel resistore è uguale alla potenza
continua dissipata nello stesso resistore quando è collegata a una tensione continua costante di
valore Veff .
Compreso il perché della preferenza accordata alla corrente alternata sulla continua, e capito cosa
rappresenta il valore 220V di tensione, ci si chiede come è realizzato l'impianto di casa con il quale
è possibile contemporaneamente accendere delle luci, ascoltare della musica, tenere in funzione il
forno elettrico. Che tipo di configurazione circuitale rende possibile tutte queste operazioni in
contemporanea? In altre parole la lampada che illumina la cucina è in serie o in parallelo con lo
stereo che diffonde musica dalla camera da letto?
Con 2÷3 lampadine, di cui una fulminata, ed un generatore di tensione si realizza un circuito in cui
tutte le lampadine sono poste in parallelo, l'altro in cui sono in serie.
Nella configurazione circuitale in serie le lampadine, sebbene alimentate, restano spente; mentre
nella configurazione in parallelo la lampadina fulminata rimane spenta, le altre sono accese! Se in
un circuito in serie c'è una lampadina fulminata anche le altre non si accendono: il circuito è aperto.
alimentatore
Le lampadine dell'impianto di casa hanno un unico alimentatore che è la linea elettrica, quindi,
poiché anche se non si cambiano le lampadine fulminate le altre di casa si accendono, si deduce che
gli utilizzatori sono posti tutti in parallelo. Infatti quando si pigia sull'interruttore si accende la sola
lampadina collegata all'interruttore, tutte le altre rimarranno spente, vedi figura precedente.
Viceversa se si spegne una lampadina, sempre in un circuito in parallelo, tutte le altre rimangono
accese; comportamento che non potrebbe mai verificarsi se si spegne una lampadina, o si fulmina,
in un circuito dove gli utilizzatori siano posti in serie.
Ma come mai allora le lampadine dell'albero di Natale si spengono tutte assieme? Perché esse sono
in serie, perché sarebbe difficile costruire piccole lampadine funzionanti alla tensione di rete di 220
V. Invece con un collegamento in serie, di 15÷20 lampadine funzionanti ad una tensione di circa 10
V, è possibile utilizzare la tensione di rete senza essere costretti ad utilizzare un trasformatore. Se
la serie dell'albero di natale non si accende più è facilmente individuabile lampadina fulminata
Progetto LES
Sceneggiatura Circuiti 3 ver.
sett..2002
utilizzando una pila da 4,5 V e provando ad accenderle singolarmente. Una volta individuata quella
fulminata, per ripristinare il funzionamento del cordone, è possibile o sostituirla oppure eliminarla e
collegare tra loro i fili della lampadina precedente con quelli della successiva.
Con una basetta, un generatore, una lampadina ed un cavetto, quest'ultimo con veci di interruttore,
schematizziamo e poi realizziamo un semplice circuito generatore - lampadina - interruttore che
possa essere rappresentativo dell'impianto d'illuminazione di casa
L'accensione/spegnimento di un interruttore si traduce, rispettivamente, in circuito chiuso/aperto.
Nell'impianto d'illuminazione di casa non c'è sempre un unico interruttore per ogni lampadina: la
luce delle scale, ad esempio, è possibile accenderla al pianterreno e spegnerla ad un piano superiore.
Stiamo parlando di un derivatore.
Potenza ed energia
Nelle nostre case l’energia elettrica consumata viene misurata da uno strumento chiamato contatore.
Su ogni contatore sono presenti alcune informazione tra le quali la potenza massima (in media 3kW
per un’utenza domestica) e il fattore di taratura, cioè il numero di giri del disco corrispondenti a
1kWh (la scrittura 1 kWh = 684 giri vuole dire che un giro completo della ruota corrisponde
all’assorbimento di 1/684 kWh).
E' possibile, quindi, utilizzare il contatore per misurare i consumi di un utilizzatore.
Scegliamo un elettrodomestico che assorba energia elettrica in modo costante nel tempo, cioè che
funzioni in modo “continuo”, una stufa elettrica ad esempio. Calcoliamo il valore dell'energia
assorbita moltiplicando il valore della potenza, dichiarato sull'elettrodomestico, per il tempo durante
il quale lo si vuole far funzionare.:
E teor. consumata (kWh) = potenza (kW) ⋅ tempo di utilizzo (h)
Confrontiamo questo valore calcolato con quello ottenuto sperimentalmente tramite le misure. Per
effettuare questa misura è necessario staccare dalla rete tutti gli altri utilizzatori. Tieniamo in
funzione l'utilizzatore per almeno 10 minuti contando il numero di giri fatti dal contatore. L'energia
assorbita dall'utilizzatore è:
E sper. consumata (kWh) = numero di giri ⋅ kWh/giro
I due valori ottenuti, entro gli errori sperimentali, coincidono.
Spunti per un'attività di laboratorio
Misure con il contatore di energia elettrica.
L'esperienza prima descritta è possibile ripeterla con un utilizzatore che funzioni in modo non
continuo, un termosifone elettrico ad esempio.
Progetto LES
Sceneggiatura Circuiti 3 ver.
sett..2002
In questo caso non si avrà un consumo costante ma si avranno dei momenti di calo intervallati da
momenti di sovraccarico. E' possibile quindi calcolare i consumi durante le diverse fasi e
confrontarli con il valore della potenza nominale riportato sull'elettrodomestico.
I consumi di energia elettrica
La potenza misura la velocità con cui l'energia di un sistema si trasforma nel tempo, caratterizza la
velocità con cui un sistema assorbe o produce lavoro.
Gli elettrodomestici hanno un consumo di energia elettrica che varia a seconda del tipo, e che, a
parità di apparecchio, cambia se questo è di ultima generazione o è di tipo tradizionale.
Si provi a stilare un classifica dei consumi in un bimestre dei principali apparecchi utilizzati in casa.
Consumi medi di una famiglia tipo in un bimestre
(kWh) 200
160
120
80
40
asciugacapelli
ferro da stiro
televisore
forno elettrico
congelatore
frigorifero
lavastoviglie
lavatrice
scaldabagno
0
Questo istogramma rappresenta i consumi energetici medi di una famiglia tipo in un bimestre; esso
ci dice che sulla bolletta incide in misura maggiore lo scaldabagno della lavatrice. Ma nel leggere
questo grafico bisogna fare attenzione perché il consumo dei diversi elettrodomestici non è
considerato a parità di tempo di utilizzo. Ad esempio lo scaldacqua è considerato costantemente in
funzione, la lavatrice invece che esegue 5 lavaggi a settimana.
Facciamo una stima del consumo energetico di due elettrodomestici a parità di tempo di utilizzo.
Una lavatrice in una famiglia media esegue 5 lavaggi a settimana, in un bimestre 40, il consumo in
kWh per ogni lavaggio è di circa 1,93. Una lavastoviglie invece esegue 1 lavaggio al giorno, in n
bimestre saranno 80, il consumo in kWh per ogni lavaggio è di circa 1,78. Quindi sulla bolletta
incide maggiormente il consumo della lavastoviglie rispetto alla lavatrice, ma è quest'ultima che
consuma di più durante un lavaggio.
Spunti per un approfondimento
I pericoli della corrente elettrica.
Ai ragazzi viene ripetuta, innumerevoli volte, la raccomandazione: "Stai attento, la corrente elettrica
è pericolosa!". Ma cosa accade ad una persona quando tocca le prese e/o i fili di un impianto
elettrico?
Il corpo umano si comporta come un conduttore che chiude il circuito formato dal cavo e dalla
Terra; con la corrente solitamente entra nel corpo attraverso le mani ed esce attraverso i piedi. Le
Progetto LES
Sceneggiatura Circuiti 3 ver.
sett..2002
lesioni riportate dal nostro corpo dipendono sia dall'intensità della corrente, sia dal tipo di corrente
(continua o alternata) ed infine dalla durata dell'azione. A parità d'intensità di corrente è quella
alternata la più pericolosa perché provoca forti contrazioni muscolari: mentre la corrente continua
non produce che una eccitazione di breve durata alla chiusura e all'apertura del circuito, la corrente
alternata provoca un'eccitazione ad ogni alternanza. Le ricerche effettuate sulla nocività della
corrente alternata hanno mostrato che essa dipende dalla frequenza e raggiunge un massimo per una
frequenza compresa tra 50 e 100 Hz. La frequenza della corrente distribuita dalle centrali elettriche
cade proprio nell'intervallo di frequenze dove è massima la nocività!
Una corrente in alternata di qualche mA provoca solo del solletico, mano a mano che l'intensità
cresce si hanno: ustioni, la contrazione dei muscoli toracici con blocco della respirazione, la
fibrillazione del cuore, il blocco del sistema nervoso. Lesioni mortali vengono provocate da correnti
alternate che superano i 100 mA.
Il corpo umano, poiché è prevalentemente formato da acqua in cui sono disciolti dei sali, si
comporta come un conduttore. La nostra pelle ha una resistenza elettrica che, a differenza di quella
di conduttori metallici e delle soluzioni, non è una grandezza ben determinata e costante per una
data temperatura ma varia, da 20 kΩ a 500 kΩ, a seconda di qual è la parte interessata al passaggio
di corrente, dal tipo di corrente che lo attraversa (corrente continua o corrente alternata), dal tipo di
contatto (secco o umido). La lingua è la parte del nostro corpo più sensibile al passaggio di corrente,
infatti l'adoperiamo per renderci conto se una pila è carica o meno, ed è la parte del nostro corpo
che mostra la più bassa resistenza.
Discutere su che cosa è un filo di terra e qual è la sua funzione. Ricordare che "le parti di un
elettrodomestico attraversate dalla corrente sono rivestite di materiale isolante: qualora si verifichi
un difetto in tale isolamento, una persona che entri in contatto con la parte metallica non più isolata
rischia di essere attraversata da una corrente intensa. La presenza del filo di terra, in parallelo alla
persona, scongiura questo pericolo: essendo infatti la resistenza di questo filo molto bassa, la
corrente passa quasi interamente attraverso di esso"
Inoltre il contatore ha un dispositivo, detto salvavita, che interrompe il flusso di corrente quando si
verifica una dispersione di corrente. Il salvavita è un interruttore differenziale con sensibilità 30
mA. E' un dispositivo installato dopo il contatore che interrompe il circuito elettrico in caso di
dispersione o "scosse".
BIBLIOGRAFIA
"Fisica" W. C. Bolton, Zanichelli Editore
"Fisica II" Silvestrini - Mencuccini, Liguori Editore
"Biografia della Fisica" G. Gamov, Edizioni Scientifiche e Tecniche Mondadori
“Fisica” H. C. Ohanian, Editore Zanichelli
"Misure elettriche e fondamenti di elettronica" E. Burattini - C. Sciacca, Liguori editore.