Ordinamento di un array
(insertion sort)
●
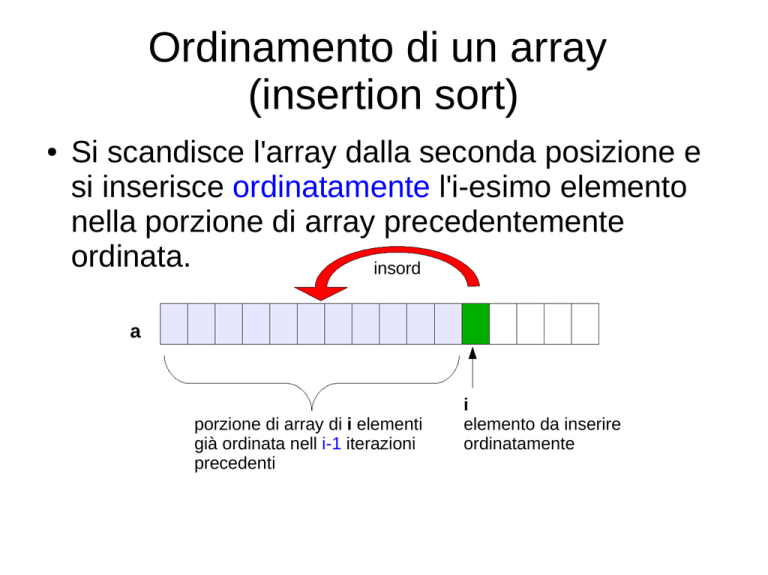
Si scandisce l'array dalla seconda posizione e
si inserisce ordinatamente l'i-esimo elemento
nella porzione di array precedentemente
ordinata.
insord
a
porzione di array di i elementi
già ordinata nell i-1 iterazioni
precedenti
i
elemento da inserire
ordinatamente
Insertion sort (sol)
void insord(int A[], int k, int x){
k--;
while (k >= 0 && A[k]>x){
A[k+1] = A[k];
--k;
}
A[k+1]=x;
}
void insertionsort(int A[], int n){
int i;
for (i=1; i<n; i++)
insord(A,i,A[i]);
}
Inserisci ordinatamente A[i]
in A[0..i-1]
Insertion sort: tempo di esecuzione
●
●
Il caso peggiore si ha quando gli elementi sono
disposti in ordine decrescente.
Il numero di operazioni (scambi e confronti) è
dato da:
iterazione (i)
1
2
3
..
n-1
●
scambi
1
2
3
..
n-1
n−1
2
n⋅n−1 n −n
2
T n=∑ i=
=
=O n
2
2
1
Se gli elementi sono già ordinati il numero di
confronti è pari a n
Ordinamento di un array
(selection sort)
●
Scandisci l'array e all'i-esima iterazione
seleziona il più piccolo elemento nella porzione
di array dalla i-esima posizione al termine
dell'array e scambialo con la posizione i-esima.
scambia
minore : elemento da
scambiare
a
porzione di array di i elementi
già ordinata nell i-1 iterazioni
precedenti
porzione di array da ordinare
Selection sort (sol)
int minimo(int A[], int inf, int sup){
int i,m;
m=inf;
for (i = inf+1; i<=sup; i++)
if (A[i]<A[m])
m = i;
return m;
}
void selsort(int A[], int n){
int i;
for (i = 0; i < n-1; i++){
int m;
m = minimo(A,i,n-1);
scambia(&A[i],&A[m]);
}
}
Minimo nella porzione di
array: A[inf .. sup]
Seleziona il minore
nella porzione di
array A[i .. n-1]
Selection sort (sol alt)
int minimo(int A[], int n){
int i,m;
m=0;
for (i = 1; i < n; i++)
if (A[i]<A[m])
m = i;
return m;
}
void selsort(int A[], int n){
int i;
for (i = 0; i < n-1; i++){
int m;
m = minimo(A+i,n-i)+i;
scambia(&A[i],&A[m]);
}
}
Minimo in un array di n
elementi
Seleziona il minore
nella porzione di
array A[i .. n-1]
Selection sort: tempo di esecuzione
●
●
Il caso peggiore si ha quando gli elementi sono
disposti in ordine decrescente.
Il numero di operazioni è dato da:
iterazione (i)
0
1
2
..
n-2
●
confronti
n-1
n-2
n-3
..
1
n−1
2
n⋅n−1 n −n
2
T n=∑ i=
=
=O n
2
2
1
Se gli elementi sono già ordinati il numero di
confronti è ancora O(n2)
Ordinamento di un array
(bubble sort)
●
●
●
Si eseguono scansioni successive dell'array; ad
ogni scansione si scambiano elementi
successivi fuori ordine.
L'algoritmo termina quando si esegue una
scansione senza scambi
E' vantaggioso per array quasi ordinati
Bubble sort (sol)
void bubblesort(int A[], int n){
int scambiato;
do{
int i;
scambiato=0;
for (i = 0; i < n-1; i++)
if (A[i] > A[i+1]){
scambiato=1;
scambia(&A[i],&A[i+1]);
}
}while (scambiato);
}
Ciclo di scansione di
elementi consecutivi
Bubble sort (sol alt)
●
●
●
Al termine della prima scansione l'elemento più
grande sarà in fondo all'array
In generale, dopo una scansione, dalla
posizione dell'ultimo scambio effettuato fino al
termine dell'array gli elementi sono ordinati
Se si ricorda la posizione dell'ultimo scambio è
possibile ridurre il tempo di esecuzione
ottenendo un algoritmo più efficiente
Bubble sort (sol alt)
void bubblesort(int A[], int n){
int scambiato, u=n-1;
do{
int i,l;
scambiato=0;
for (i = 0; i < u; i++)
if (A[i] > A[i+1]){
scambiato=1;
scambia(&A[i],&A[i+1]);
l = i;
}
u = l+1;
}while (scambiato);
}
Estremo superiore di
scansione non più
costante
ricorda la posizione
dello scambio
aggiorna l'estremo
superiore della
scansione
Bubble sort: tempo di esecuzione
●
●
Il caso peggiore si ha quando gli elementi sono
disposti in ordine decrescente.
Il numero di operazioni (scambi e confronti) è
dato da:
iterazione (i)
1
2
3
..
n-1
●
scambi
1
2
3
..
n-1
n−1
2
n⋅n−1 n −n
2
T n=∑ i=
=
=O n
2
2
1
Se gli elementi sono già ordinati il numero di
confronti è pari a n
Bubble sort
●
●
Si può migliorare ulteriormente l'efficienza del
bubble sort effettuando scansioni alternate
verso l'alto e verso il basso aggiornando gli
estremi della scansione con le posizioni
dell'ultimo scambio.
Il caso peggiore rimane sempre O(n2)
Bubble sort (sol alt)
void bubblesort(int A[], int n){
int d, inf, sup, scambiato;
d=0; inf=0; sup=n-1;
do{
Scansione
per indici
crescenti
...
d=!d;
scambiato=0;
if (d){
int i, ultimo;
for (i=inf; i<sup; i++)7
if (A[i]>A[i+1]){
scambia(&A[i], &A[i+1]);
ultimo=i;
scambiato=1;
}
sup=ultimo;
}else
Variabile per
alternare le
scansioni
Memorizza l'indice
dello scambio
L'indice dell'ultimo
scambio diventa
l'estremo superiore
per la prossima
scansione
Bubble sort (sol alt)
...
{
Scansione
per indici
decrescenti
}
int i, ultimo;
for (i=sup; i>inf; i--)
if (A[i]<A[i-1]){
scambia(&A[i], &A[i-1]);
ultimo=i;
scambiato=1;
}
inf=ultimo;
Memorizza l'indice
dello scambio
}
}while (scambiato);
L'indice dell'ultimo scambio
diventa l'estremo inferiore per
la prossima scansione












