Matematica Generale
Rita Laura D’Ecclesia
Università di Roma “La Sapienza”
Email:[email protected]
Web: http://w3.uniroma1.it/decclesia
1-1
1
1.1 Introduzione di modello matematico
1. Le ipotesi
2. Le componenti
3. La soluzione
Le ipotesi
Esempio classico: modello di domanda e offerta
Agenti= aziende, consumatori e governi.
Contesto economico= domanda e offerta possono essere descritte da
un modello lineare (semplice)
Scelte effettuate in un mondo “razionale”
Equilibrio: Il risultato delle scelte operate dagli agenti. Un modello
è in equilibrio quando variazioni delle variabili vengono causate solo
da variazioni del contesto economico. I valori di equilibrio delle
variabili economiche sono “endogeni”- vengono determinati
all’interno del modelli- e dipendono da variabili “esogene”.
Cambiamenti: Analizzare come l’equilibrio può essere modificato in
seguito a variazioni delle condizioni economiche
1-1
3
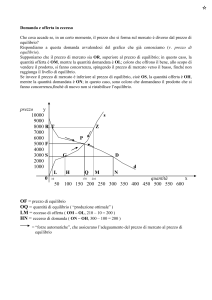
Il modello di Domanda e Offerta
Gli agenti in questo modello sono consumatori e aziende.
Il comportamento della domanda di beni e dell’offerta
possono essere descritte da modelli lineari.
C’è una relazione inversa tra prezzo e domanda del bene, e
una relazione diretta tra offerta e prezzo del bene che posso
descrivere con le seguenti curve:
Domanda
P = a − bQD
Offerta
P = c + dQs
[1]
[2]
P= prezzo del bene, QD= quantità domandata; Qs= quantità offerta
1-1
4
Le componenti
a e b sono parametri esogeni che dipendono da molti fattori
quali le preferenze dei consumatori e il loro reddito
ced
(esogeni) dipendono dai prezzi delle materie prime e degli
input tecnologici e fattori produttivi
P ,Qs e Qd sono le variabili endogene che vengono determinate
come soluzione del nostro semplice modello
a > 0, c < a
a>0; b>0
c ≥ 0
c+d >0
d ≥ 0
c>0; d>0
1-1
5
La soluzione (1)
La soluzione del modello- il prezzo e la quantità domandata ed
offerta di equilibrio- si ottiene trovando il punto di intersezione fra
la curva di domanda e la curva di offerta:
1. Intersezione delle due curve (metodo grafico):Qs=Qd
2. Algebra Matriciale
3. ….
1-1
6
La soluzione (1)
Il primo semplice approccio per risolvere tale problema e trovare la
quantità di equilibrio è porre la quantità domandata uguale alla
quantità offerta:
Qs = Q D = Q
[3]
Sostituendo le espressioni riportate nella 1 e nella 2 abbiamo
a − bQ = c + dQ
[4]
a − c = (b + d )Q
Q
*
(
a − c)
=
(b + d )
1-1
[5]
7
La soluzione (2)
Per avere il prezzo di equilibrio dobbiamo risolvere il sistema
sostituendo nelle due equazioni il valore di equilibrio per Q*
(
a − c)
P =c+d
(b + d )
Usando l’equazione
dell’offerta [2]
Usando l’equazione della
domanda [1]
P
*
c(b + d ) + d (a − c )
P=
(b + d )
(
ad + bc )
=
(b + d )
1-1
[6]
[7]
[8]
8
La soluzione (3)
Abbiamo quindi trovato la soluzione in FORMA RIDOTTA (i valori
delle variabili endogene in funzione delle variabili esogene)
P
*
(
ad + bc )
=
(b + d )
[9]
Una volta risolto in funzione delle variabili esogene e trovato
l’equilibrio possiamo studiare come varia questo equilibrio al variare
di una delle variabili esogene:
STATICA COMPARATA
1-1
9
Statica Comparata
Matematicamente ciò implica calcolare le derivate o più
genericamente le derivate parziali della soluzione trovata in funzione
dei parametri
P = f (a, b, c, d ) ≡ f ( x1 , x2 , x3 , x4 )
*
[10]
Ma siamo in grado di fare queste operazioni???
Dobbiamo introdurre prima i seguenti concetti:
-vettori, spazi vettoriali, algebra matriciale, funzioni in Rn,
calcolo differenziale in Rn….etc.etc.
1-1
10
La soluzione (1a)
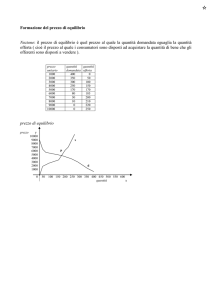
La soluzione del modello- inserendo al posto dei parametri dei
numeri reali: a=2, b=3, c=1,d=2
2 − 3Q = 1 + 2Q
Q
*
(
2 − 1) 1
=
=
(3 + 2) 5
Ha senso? Che vuol dire produrre 1/5 di prodotto?
1-1
11