er
rD
riv
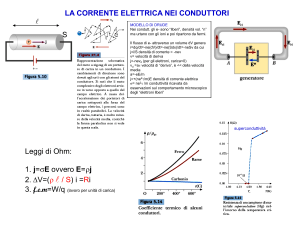
Correnti stazionarie nel diodo a vuoto
tib
le
Pr
∂ρ
∂t
pa
div J = −
in
te
Il punto di partenza della nostra analisi sarà la legge di conservazione della carica:
PD
F
C
om
la quale esprime il legame fra la variazione temporale, in una certa regione di spazio, della
densità di carica in essa contenuta e il flusso della densità di corrente che ne attraversa la
frontiera.
n
of
th
e
Prima di continuare, ricordiamo che quanto esposto è in parte l’argomento del paragrafo 4.2 e la
soluzione del problema 4.25 de LA FISICA DI BERKELEY, ELETTRICITA’ E MAGNETISMO. Per
questa ragione le unità usate sono quelle C.G.S..
io
J è data da ρ v , dove v è la velocità degli elettroni in quella
de
m
o
ve
rs
La densità locale di corrente
regione.
J x = J y = 0 . Se poi la corrente è stazionaria
∂ρ
= 0.
∂t
ith
th
e
Nel caso di un diodo a placche parallele
w
∂J x
= 0 e quindi ρ v x = costante.
∂x
v x non è costante: essa varia lungo x in quanto gli
ge
ne
ra
te
d
Avremo quindi
Th
is
fil
e
w
as
elettroni vengono accelerati dal campo elettrico. Se ne
conclude che anche ρ non è costante: la densità di
elettroni è elevata presso il catodo e bassa verso
l’anodo, esattamente come la densità di auto in una
autostrada, che è alta dove vi è un rallentamento nel
traffico, bassa dove il traffico è veloce.
La presenza di una certa densità di carica negativa (la cosiddetta «carica spaziale») influenza il
campo elettrico, e, di conseguenza, l’accelerazione e la velocità degli elettroni, e, per completare
il ciclo, la stessa densità elettrica.
Queste interrelazioni sono essere descritte dalle seguenti equazioni:
equazione di Poisson:
(1)
d 2V
= −4πρ ,
dx 2
equazione del moto degli elettroni:
(2)
1 2
mv = eV ( x ) ,
2
legge di conservazione della carica
(3)
ρv = J = −
I
,
A
le condizioni al contorno
(4)
V ( x ) x =0 = 0
e V ( x)
x=s
= Va .
rD
riv
er
Sostituendo la (3) nella (1) e usando quindi la (2) si ottiene:
in
Pr
le
tib
dV
e otteniamo:
dx
pa
2
e
PD
F
dV d 2V
I
m dV − 1 2
= 4π ⋅
2
V
2
dx dx
A 2e dx
th
2
C
om
Moltiplichiamo ambo i membri della (5) per
te
d 2V
I 1
I
m − 12
= −4πρ = 4π ⋅ = 4π ⋅
V
2
dx
A v
A 2e
(5)
2
rs
ve
de
m
o
(6)
d dV
I
m d 12
V
= 16π ⋅
dx dx
A 2e dx
io
n
of
e quindi
x =0
=
dV
dx
= 0.
x =0
w
ith
th
e
Per risolvere la (6) dobbiamo imporre l’ulteriore vincolo E
d
< 0 gli elettroni emessi dal catodo ne sarebbero immediatamente riassorbiti, se
te
x =0
ra
Se E
ge
ne
E x =0 > 0 il “vento” di elettroni emessi dal catodo spazzerebbe via la «carica spaziale». In
w
as
ambedue le situazioni il diodo sarebbe instabile. I vincolo E
x =0
= 0 ci dice che l’effetto di
Th
is
fil
e
schermatura della «carica spaziale» è così grande che non vi possono essere elettroni che
attraversano il diodo, anche se altri ne venissero emessi dal catodo.
Con tale vincolo la (6) ha come soluzione
(7)
1
dV
=V 4
dx
La soluzione della (7) che soddisfa alle condizioni al contorno (4) è data da
V = Va s
−4
3
x
4
3
La corrente circolante nel diodo è allora data da:
I = − Aρv =
A d 2V
2e 1 2
A
⋅
V =
2
4π dx
m
4π
2 e − 4 3 4 1 − 2 3 1 2 − 2 3 2 3
⋅ x Va s x
Va s
m
3 3
semplificando e disponendo i termini si ha:
(8)
I=
A
9π
3
2e − 2 1 2
s Va Va = kVa 2
m
Questa legge è stata per la prima volta derivata da Child1.
Si può vedere che il termine A
e −2 12
s Va ha le dimensioni dell’inverso di una resistenza
m
(ricordiamo che stiamo lavorando in unità C.G.S., vedi terza di copertina del libro citato):
1
1
in
te
rD
riv
er
1
e −2 1 2 e 1 2
ues 2
erg 2 grammo 2 cm cm
s Va =
Va =
⋅
=
=
A
1
1
1
m
m
grammo 2 ues 2 grammo 2 sec sec
pa
tib
le
Pr
Possiamo a questo punto notare che gli elettrono emessi dal catodo di un diodo reale non
emergono con velocità rigorosamente nulla, ma piuttosto con velocità che dipendono dalla
temperatura del catodo.
PD
F
C
om
Questo corrisponde a un’energia cinetica di 1/10 di eletton-volt, circa. Fintanto che abbiamo a
che fare con potenziali molto maggiori, si può, con buona approssimazione assumere nulla la
velocità iniziale.
n
of
th
e
La legge di Child (8) è stata estesa da Langmuir 2, il quale ha ottenuto, per una velocità iniziale
degli elettroni non nulla, la:
de
m
o
ve
rs
io
3
0.0247 T
I = kVa 2 1 +
Va
w
ith
th
e
dove T è la temperatura, in °K, del catodo. Per una trattazione più dettagliata vedasi Harper e
Perugini3.
ra
te
d
Fatti i debiti paragoni, e supponendo che l’effetto schermante della griglia sia lineare sì da poter
invocare il principio di sovrapposizione, la (8) ci fornisce la giustificazione della
ge
ne
I a = k (Va + µV g )
3
2
as
(9)
Th
is
fil
e
w
valida, in prima (e ragionevole) approssimazione per un triodo4. Notare come qui e nel seguito
scriveremo Va al posto di Vak e V g al posto di V gk .
1
Child, Phys. Rev., Vol. 32, 498 (1911)
2
Langmuir, I., “The effects of Space Charge and Initial Velocities on the Potential Distribution
and Thermionic Current between Parallel Plane Electrodes”, Phys. Rev., Vol. 21 (April 1923)
3
Harper, J., Glass Audio 2/99 e Perugini, S., ibidem 4/98
4
Valori delle costanti per la (9) per un insieme interessante di triodi si possono trovare su:
http://www.geocities.com/CapeCanaveral/Lab/4422/ .