Lezioni da Matematica I Calcolo differenziale, Algebra

Lezioni da Matematica I
Calcolo differenziale, Algebra lineare,
Probabilità e statistica
G. Aletti & G. Naldi & L. Pareschi
http://www.ateneonline.it/naldi matematica
McGraw-Hill
Capitolo 2, Limiti e continuità
1
Limiti e continuità
Limite: concetto cardine alla base di molte costruzioni del Calcolo
Differenziale.
• Esempi
• Definizione di limite
• Limite destro e sinistro
limx→x0 f (x) = L
Iniziamo con alcuni problemi ...
2
Problema A (buona definizione delle funzioni).
Abbiamo definito (con a > 0 base)
ar , r ∈ Q
ma se desideriamo calcolare ax , x ∈ R?
Possiamo considerare una successione di valori razionali {rk }
sempre più vicini a x e poi “osservare” se
ar k
si avvicina al valore y.
Possiamo definire y = ax , ma è una buona definizione? Dipende
dalla scelta della successione di valori rk ? Cosa significa “vicino”?
25
???
20
15
10
5
0
0
0.5
1
1.5
2
2.5
3
Figura 2.1: Dove va a finire ark (cerchietti)? e ark (crocette)?.
3
Problema B (Approssimazioni successive)
Calcoliamo l’area di un cerchio di raggio r approssimando tale
area con l’area An di un poligono regolare inscritto con n lati uguali.
Abbiamo
S
M
π /n
r
O
R
Figura 2.2: Calcolo di un’area come limite di aree approssimanti.
An = nr2 sin(π/n) cos(π/n),
cosa possiamo dire di A − n al crescere di n? In simboli la domanda
si scrive
lim An =?
n→+∞
Sospettiamo (desideriamo) che
lim An = πr2
n→+∞
4
Problema C (come andrà a finire?)
I grafici della retta di equazione y = x e della funzione y = sin x
passano per l’origine O ≡ (0, 0).
Cosa succede al quoziente
sin(x)
?
x
Facciamo qualche prova numerica
x
sin (x)/x
0.1250
0.0625
0.0312
0.0156
0.0078
0.9974
0.9993
0.9998
1.0000
1.0000
Tabella 2.1: Esperimenti numerici per il calcolo di f (x) = sin (x)/x per valori
di x prossimi a 0.
Questi esperimenti dovrebbero condurre alla deduzione (con scrittura ormai chiara)
sin(x)
= 1.
lim
x→0
x
5
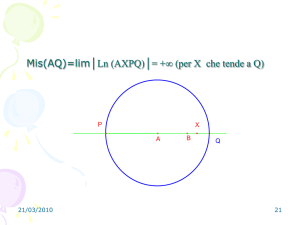
Problema D (la tangente)
Cerchiamo la posizione della retta tangente al grafico della parabola y = x2 nel punto P (1, 1) approssimandola con rette passanti per
P e per un differente punto Q del grafico. Abbiamo Q(x, x2 ) e indichiamo con mQ la pendenza della retta P Q. Per esempio con
Q(1.5, 2.25) si ottiene
mQ =
2.25 − 1
= 2.5.
1.5 − 1
Quello che vorremmo definire il “limite”
lim mQ (x) = m oppure . lim mQ (x) = m
x→1
Q→P
dove y = m(x − 1) + 1 è l’equazione della retta tangente.
7
7
6
6
5
5
f(x)=x 2
f(x)=x 2
4
4
3
3
2
2
P
1
P
1
(1,1)
0
(1,1)
0
−1
−1
retta tangente
−2
−2.5
−2
−1.5
−1
−0.5
0
0.5
1
retta tangente
1.5
2
2.5
−2
−2.5
7
7
6
6
5
−2
−1.5
−1
−0.5
0.5
1
1.5
2
2.5
2
2.5
5
f(x)=x 2
f(x)=x 2
4
4
3
3
2
2
P
1
P
1
(1,1)
0
(1,1)
0
−1
−1
retta tangente
−2
−2.5
0
−2
−1.5
−1
−0.5
0
0.5
1
retta tangente
1.5
2
2.5
−2
−2.5
−2
−1.5
−1
−0.5
0
0.5
1
1.5
Figura 2.3: Calcolo della retta tangente come limite.
6
Una parentesi un pò euristica ...
Come tradurre:
- vicino
- avvicinarsi
- Mentre x si avvicina a ... f (x) si avvicina a ...
Stare nelle “vicinanze” ∼ stare in un intorno Come si comporta f
Intorno di centro x e raggio r
0
x0−r
x0+r
x0
Intorni di "infinito"
a
a
Figura 2.4: Intorni ragionevoli.
per valori di x prossimi a x0 ?
Quali punti x0 considerare?
x0 punto di accumulazione (caso x0 ∈ R):
∀I(x0 , r) con r > 0,
∃x ∈ dom(f ) ∩ I(x0 , r) \ {x0 },
dove I(x0 ) = (x0 − r, x0 + r).
È importante la posizione di x0 rispetto a dom(f ) non che x0 ∈
dom(f ).
7
Personaggi:
• f funzione f : A → R;
• x0 ∈ R, punto di accumulazione di A.
Definizione (Usiamo gli intorni) Diremo che limx→x0 f (x) = L,
con L ∈ R, quando per ogni intorno I(L; ²), ² > 0, esiste un
intorno I(x0 ; δ), δ > 0, tale che se x ∈ I(x0 ; δ)\{x0 }, x ∈ dom(f ),
allora f (x) ∈ I(L; ²).
f
f
Intorno di L
Intorno di L
x0
x0
Intorno di x 0
Intorno di x 0
Figura 2.5: Illustrazione geometrica del concetto di limite tramite gli intorni.
8
Graficamente dovremmo aver intuito ma per fare i “conti”?
Dobbiamo descrivere un intorno.
• Cosa significa “... per ogni intorno I(L; ²)...”?
◦ Significa che possiamo scegliere arbitrariamente ² .
• Cosa significa “... esiste un intorno I(x0 ; δ) ...”?
◦ Significa che possiamo determinare un δ > 0 tale che l’intorno
I(x0 ; δ) sia adeguato.
Il gioco consiste in botta-risposta, qualcuno gioca un intorno
I(L; ²) e noi dobbiamo essere in grado di rispondere con un intorno
I(x0 ; δ).
Attenzione: basta una strategia/scelta/metodo/... per un intorno
I(x0 ; δ), non è detto che sia unico, anzi ... ne basta comunque uno.
Definizione (Notazione ²−δ) Diremo che f tende al limite L ∈ R
(o che converge ad L) per x che tende ad x0 se ∀² > 0 si pu trovare
un δ > 0 tale che
|f (x) − L| < ²
se 0 < |x − a| < δ,
x ∈ dom(f ).
.
Esercizio, si dimostri, attraverso la definizione, che
lim (4x − 5) = 7.
x→3
9
Proprietà fondamentali:
- il limite (quando c’è) è unico;
- il limite è compatibile con le operazioni aritmetiche, per
esempio se
limx→x0 f (x) = L1
limx→x0 g(x) = L2
con L1 , L2 ∈ R, allora
lim (f (x) + g(x)) = lim f (x) + lim g(x) = L1 + L2 .
x→x0
x→x0
x→x0
L
f
f
L’
x
0
Figura 2.6: Illustrazione grafica dell’unicità del limite.
10
Non sempre i limiti esistono. Consideriamo la funzione (funzione
segno) definita per x 6= 0,

1
se x > 0
|x| 
,
sign(x) =
=
 −1 se x < 0
x
non esiste il limite
lim sign(x).
x→0
Infatti in ogni intorno di x0 = 0 vi sono punti x e punti x tali che
sign(x) = −1, sign(x) = 1.
Se invece conosciamo alcuni limiti altri si possono dedurre tramite
il
Teorema (di compressione o dei due carabinieri). Se f, g, h :
A → R, x0 punto di accumulazione di A, g(x) ≤ f (x) ≤ h(x)
per x ∈ dom(f ) \ {x0 }, 0 < |x − x0 | < r per un certo r > 0, e se
limx→x0 g(x) = limx→x0 h(x) = L allora limx→x0 f (x) = L.
h
h
f
g
f
g
x0
Figura 2.7: Illustrazione geometrica del teorema di compressione.
11
Qualche volta lo zero vince
Mostriamo che
1
= 0.
x→0
x
Non possiamo usare la regola del prodotto,
lim x2 sin
lim x2 sin
x→0
1
1
= lim x2 · lim sin =?
x→0
x→0
x
x
Abbiamo invece
−1 ≤ sin
1
≤ 1, x 6= 0,
x
quindi
1
≤ x2 , x 6= 0,
x
−x2 ≤ x2 · sin
da cui (Teorema due carabinieri)
lim x2 sin
x→0
1
= 0.
x
In generale: “Il prodotto di una funzione infinitesima per una funzione limitata è una funzione infinitesima”.
12
Estensioni del concetto di limite
Vi sono vari modi per estendere il concetto di limite, noi considereremo le seguenti,
• limite destro, limite sinistro (cio quando x tende a x0 solo da
“un lato”);
• limiti all’infinito (quando x diventa arbitrariamente grande,
positivo o negativo);
• limiti infiniti (quando f diventa arbitrariamente grande, positiva o negativa).
Definizione (Limite destro) Sia f : A → R, si dice che la funzione
f ha limite destro L per x che tende a x0 , e si scriver
lim f (x) = L
x→x+
0
se ∀² > 0, esiste δ > 0 tale che
|f (x) − L| < ² quando x0 < x < x0 + δ,
x ∈ dom(f ).
In questo caso, x0 deve essere tale che ∀δ > 0 esista almeno un
x ∈ dom(f ) tale che x0 < x < x0 + δ.
Per li limite sinistro la definizione è analoga (con le modifiche
intuitive del caso). Per esempio,
lim sign(x) = 1,
x→0+
lim sign(x) = −1.
x→0−
Nota: se limite destro e sinistro esistono e sono uguali allora esiste
anche il limite ed è uguale al valore comune.
13
Limiti all’infinito, limiti infiniti
Per una successione f : N → R, non ha senso porsi il problema
(n ∈ N)
lim f (x).
x→n
Ogni singolo punto n ∈ N è isolato, la domanda ragionevole invece
riguarda il comportamento di f al crescere di x.
Consideriamo il caso di f : A ⊆ R → R con x0 = +∞ punto di
accumulazione: ∀a ∈ R si ha (a, +∞) ∩ A 6= ∅.
Quindi
limx→+∞ f (x) = L ∈ R
significa che ∀² > 0 esiste un valore a ∈ R tale che
|f (x) − L| < ² quando x ∈ A ∩ (a, +∞).
Sia ora x0 punto di accumulazione di A, la scrittura
limx→x0 f (x) = +∞
significa che f diventa arbitrariamente grande per x che si avvicina
a x0 , in altri termini: per ogni M > 0 esiste δ > 0 tale che
f (x) > M quando 0 < |x − x0 | < δ, x ∈ A.
Nota: Definizioni analoghe nel caso di limiti per x → −∞ e
limite infinito −∞.
14
Possiamo combinare tra di loro i vari casi, anche per i
limiti destri e sinistri.
f
M
M
f
(B)
f
(A)
a
x −δ
x +δ
0
0
x
L+ ε
0
L −ε
L
x −δ
0
x0
a
(C)
(D)
−M
Figura 2.8: Illustrazione grafica di alcuni limiti, (A) f → +∞, per x → x0 ; (B)
f → +∞, per x → +∞; (C) f → −∞, per x → x−
0 ; (D) f → L, per x → +∞.
15
Continuità
Iniziamo considerando la continuità in un punto x0 .
Definizione (funzione continua in un punto)Siano f : A ⊆
R → RSiano e x0 ∈ A punto di accumulazione di A. La funzione f
è detta continua nel punto x0 se
lim f (x) = f (x0 ).
x→x0
Osserviamo che,
• il limite deve esistere;
• il limite deve essere finito (deve appartenere a R);
• il limite deve coincidere con f (x0 ).
Notazione ² − δ,
∀² > 0, ∃δ > 0 tale che ∀x ∈ dom(f ), |x−x0 | < δ implica |f (x)−f (x0 )| < ².
Teorema (Continuità e operazioni).Siano f e g due funzioni
continue in x0 e definite in un intervallo contenente x0 , allora le
funzioni f + g, f − g, f g sono continue in x0 . Se c ∈ R è anche
la funzione c · f è continua in x0 . Se inoltre g(x0 ) 6= 0, la funzione
f /g è continua in x0 .
16
Alcune funzioni continue
• lineari, quadratiche;
• funzioni polinomiali;
• funzioni trigonometriche elementari;
• funzioni esponenziali e logaritmiche.
Non sempre la verifica è immediata (tramite le operazioni aritmetiche elementari). Esempio di strumento utile.
Teorema(Continuità e composizione)Siano f e g due funzioni
per cui è definita la funzione composta f ◦ g. Se f è una funzione
continua in y0 e se
lim g(x) = y0 ,
x→x0
allora
lim f (g(x)) = f (y0 ) = f
x→x0
µ
¶
lim g(x) .
x→x0
In particolare, se g è continua in x0 allora la funzione composta f ◦g
è continua in x0 .
Per esempio la funzione f (x) = sin3 (x2 ) + 5 cos (7x) è continua
in ogni punto x ∈ R.
Esempio di discontinuità, f (x) = [x] (funzione parte intera) è
discontinua in tutti i punti x ∈ Z (e continua negli altri punti non
interi).
17
4
3
2
1
0
−1
[x]
−2
−3
−4
−5
−5
−4
−3
−2
−1
0
1
2
3
4
5
Figura 2.9: Funzione parte intera [x].
Albero delle discontinuià. Grafici di funzioni discontinue.
18
L=f(x )
Continuità
L finito
L diverso da f(x )
Esiste L
L infinito
Discontinuità
eliminabile
Punto di infinito
L+ e L− finiti
Salto
Esistono L+ e L−
Uno infinito
Punto di infinito
Non esiste L
Discontinuità di
seconda specie
Non esiste L+ o L−
Figura 2.10: Albero decisionale per continuità e discontinuità.
Funzioni continue in un intervallo: possiamo disegnare il grafico
“senza staccare la matita dal foglio”
Consideriamo,
(I1) f : [a, b] → R, con a, b ∈ R;
(I2) f continua in ogni punto x ∈ [a, b].
In viaggio dal punto (a, f (a)) al punto (b, f (b)), dobbiamo attraversare almeno una volta punti con ordinata intermedia tra f (a) e
f (b).
19
4
100
3.5
3
90
Discontinuità eliminabile
80
2.5
70
2
60
1.5
50
1
40
0.5
30
0
20
−0.5
Punto di infinito
10
x
−1
−2
0
−1.5
−1
−0.5
0
0.5
1
1.5
2
2.5
0
−3
3
−2
−1
0
1
2
3
0.8
1
1
2
0.8
Salto
0.6
Seconda specie
1.5
0.4
0.2
1
0
x0
−0.2
−0.4
0.5
−0.6
−0.8
0
0
0.5
1
1.5
2
2.5
3
−1
−0.2
0
0.2
0.4
0.6
Figura 2.11: Vari tipi di discontinuità.
La continuità implica importanti proprietà
Teorema dei valori intermedi Sia f : [a, b] → R continua in
[a, b], se y è un numero reale compreso tra f (a) e f (b) allora esiste
un numero reale r ∈ (a, b) tale che f (r) = y.
Teorema di Bolzano o degli zeri Sia f : [a, b] → R continua in [a, b], se f (a)·f (b) < 0, allora esiste c ∈ (a, b) tale che f (c) = 0.
20
4
( b, f(b) )
3.5
3
2.5
2
y=c
1.5
1
( a,f(a) )
0.5
0
−0.5
1
1.2
1.4
1.6
1.8
2
2.2
2.4
2.6
2.8
3
Figura 2.12: Il grafico della funzione f deve attraversare la retta y = c con c
valore intermedio tra f (a) e f (b).
Teorema di Weierstrass Sia f : [a, b] → R continua in [a, b],
allora esiste un numero reale positivo k tale che
|f (x)| ≤ k, ∀x ∈ [a, b].
Esistono inoltre due punti x0 (punto di minimo assoluto) e x1 (punto
di massimo assoluto) tali che
f (x0 ) ≤ f (x) ≤ f (x1 ), ∀x ∈ [a, b].
21