caricato da
common.user11671
Elettrotecnica: Unità di Misura, Geometria Analitica e Sistemi Lineari
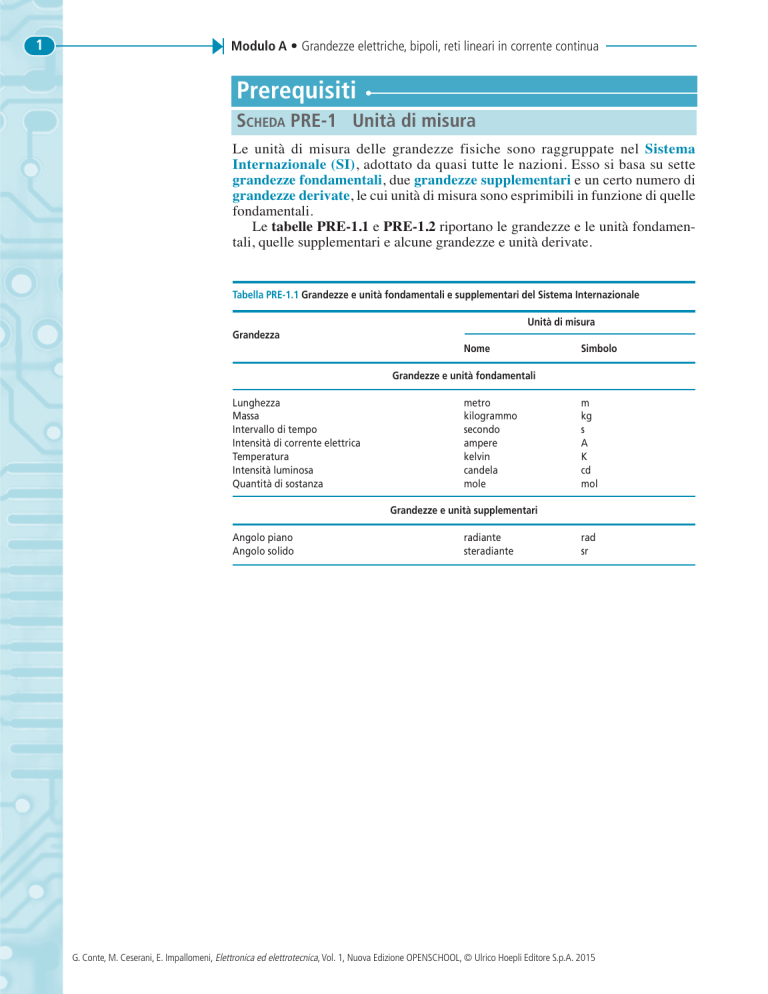
1 Modulo A • Grandezze elettriche, bipoli, reti lineari in corrente continua Prerequisiti SCHEDA PRE-1 Unità di misura Le unità di misura delle grandezze fisiche sono raggruppate nel Sistema Internazionale (SI), adottato da quasi tutte le nazioni. Esso si basa su sette grandezze fondamentali, due grandezze supplementari e un certo numero di grandezze derivate, le cui unità di misura sono esprimibili in funzione di quelle fondamentali. Le tabelle PRE-1.1 e PRE-1.2 riportano le grandezze e le unità fondamentali, quelle supplementari e alcune grandezze e unità derivate. Tabella PRE-1.1 Grandezze e unità fondamentali e supplementari del Sistema Internazionale Unità di misura Grandezza Nome Simbolo Grandezze e unità fondamentali Lunghezza Massa Intervallo di tempo Intensità di corrente elettrica Temperatura Intensità luminosa Quantità di sostanza metro kilogrammo secondo ampere kelvin candela mole m kg s A K cd mol Grandezze e unità supplementari Angolo piano Angolo solido radiante steradiante rad sr G. Conte, M. Ceserani, E. Impallomeni, Elettronica ed elettrotecnica, Vol. 1, Nuova Edizione OPENSCHOOL, © Ulrico Hoepli Editore S.p.A. 2015 2 Prerequisiti Tabella PRE-1.2 Alcune grandezze e unità derivate del Sistema Internazionale Grandezza Nome dell’unità Simbolo Definizione Area metro quadrato Volume metro cubo Forza, peso newton N kg m/s2 Pressione pascal Pa N/m2 Energia, lavoro, calore joule J Nm Velocità metro al secondo m/s Accelerazione metro al secondo quadrato m/s2 Velocità angolare radiante al secondo rad/s Accelerazione angolare radiante al secondo quadrato Potenza watt W J/s Carica elettrica coulomb C As Intensità del campo elettrico newton al coulomb m2 m3 rad/s2 N/C Tensione, differenza di potenziale elettrico, volt V Capacità elettrica forza elettromotrice farad F J/C C/V Resistenza elettrica ohm Ω V/A Resistività elettrica ohm per metro Induzione magnetica tesla T N/(A m) Flusso magnetico weber Wb T m2 Ωm Induttanza henry H Ωs Frequenza hertz Hz 1/s Regole per la scrittura delle unità di misura 1. Il simbolo dell’unità di misura segue, e non precede, il numero (esempio: 5 V e non V 5). 2. Il simbolo dell’unità di misura non deve essere seguito dal punto finale (salvo al termine della frase). 3. I prefissi devono essere maiuscoli o minuscoli a seconda dei casi, come indicato nella tabella PRE-1.3 (esempi: 10 kV e non 10 KV, 5 GW e non 5 gW). 4. L’unità di misura non accompagnata da un numero in cifre si esprime con il nome e non con il simbolo, salvo nei disegni, prospetti ecc. (esempio: due ampere e non due A). 5. I nomi delle unità di misura devono essere generalmente scritti con caratteri minuscoli, compresa la lettera iniziale, e, quando derivano da un nome proprio, sono invariabili al plurale (esempi: “la tensione vale cinque volt” e non “la tensione vale cinque Volt” o “la tensione vale cinque volts”). ESEMPI 1. 2. 3. 4. 25 mA = 25 × 10–3 A = 0,025 A 450 μF = 450 × 10–6 F = 0,450 × 10–3 F = 0,450 mF 0,15 MW = 0,15 × 106 W = 150 × 103 W = 150 kW 0,067 kJ = 0,067 × 103 J = 67 J Tabella PRE–1.3 Prefissi per le unità di misura Nome Simbolo Moltiplica per exa peta tera giga mega kilo etto deca deci centi milli micro nano pico femto atto E P T G M k h da d c m μ n p f a 1018 1015 1012 109 106 103 102 101 10–1 10–2 10–3 10–6 10–9 10–12 10–15 10–18 G. Conte, M. Ceserani, E. Impallomeni, Elettronica ed elettrotecnica, Vol. 1, Nuova Edizione OPENSCHOOL, © Ulrico Hoepli Editore S.p.A. 2015 3 Modulo A • Grandezze elettriche, bipoli, reti lineari in corrente continua SCHEDA PRE-2 Elementi di geometria analitica Piano cartesiano Il piano dotato di un sistema di riferimento cartesiano viene detto piano cartesiano. Il sistema di riferimento cartesiano è costituito da due rette, denominate asse x e asse y, perpendicolari e incidenti nel punto O, detto origine o centro del riferimento. Un qualsiasi punto P del piano (figura PRE-2.1) è completamente determinato conoscendo le distanze di P dagli assi; tali distanze sono le coordinate di P e prendono il nome di ascissa e di ordinata, con il seguente significato: • • l’ascissa xP è la distanza del punto P dall’asse y; l’ordinata yP è la distanza del punto P dall’asse x. y xP P (xP , yP) yP Figura PRE-2.1 Piano cartesiano e coordinate del punto P. x O y y x =m +q P2 Δ y = y2 – y1 P1 Figura PRE-2.2 Rappresentazione della retta y = mx + q; significato di m e di q. 冧 α Δy m = –––– = tg α Δx α Δ x = x2 – x1 q = (y)x = 0 q O x Equazione della retta L’equazione y = mx + q rappresenta una retta sul piano cartesiano, dove m è il coefficiente angolare della retta e q è il valore che assume y per x = 0 (figura PRE-2.2). Il coefficiente angolare indica la pendenza della retta rispetto all’asse x, corrisponde al rapporto Δy/Δx tra gli incrementi delle grandezze ed è pari al valore della tangente trigonometrica dell’angolo α. Si hanno i seguenti casi particolari (figura PRE-2.3): • • • • • per q = 0 la retta passa per l’origine (y = mx); per m = 0 la retta è y = q ed è parallela all’asse x; per m = 1 la retta è inclinata di 45°; per m tendente al valore infinito la retta diventa parallela all’asse y (x = k), in quanto l’angolo rispetto a x diventa di 90°; per m < 0 la pendenza diventa superiore a 90°. G. Conte, M. Ceserani, E. Impallomeni, Elettronica ed elettrotecnica, Vol. 1, Nuova Edizione OPENSCHOOL, © Ulrico Hoepli Editore S.p.A. 2015 4 Prerequisiti m m➝∞ = 1 y = x y=k + q y q= 0 x y=m Figura PRE-2.3 Rappresentazione della retta: casi particolari. α > 90° 45° x O m=0 y=q m<0 Equazione della parabola L’equazione di 2° grado y = ax2 + bx + c rappresenta una parabola con asse di simmetria parallelo all’asse y, avente vertice V di coordinate (figura PRE-2.4): b xV = – ––– 2a – b2 + 4ac yV = –––––––––– 4a y y y = x 2 – 2x + 4 (a > 0) V (xV , yV ) O x 0 x y= Figura PRE-2.4 Rappresentazione della parabola y = ax2 + bx + c. –x 2 – 2x + 2 (a < 0) Figura PRE-2.5 Parabola con concavità verso l’alto (a > 0) e verso il basso (a < 0). G. Conte, M. Ceserani, E. Impallomeni, Elettronica ed elettrotecnica, Vol. 1, Nuova Edizione OPENSCHOOL, © Ulrico Hoepli Editore S.p.A. 2015 5 Modulo A • Grandezze elettriche, bipoli, reti lineari in corrente continua y y y = x2 + 4 y = 2x 2 0 0 x Figura PRE-2.6 Parabola con b = 0 e c = 0. x Figura PRE-2.7 Parabola con b = 0. Si hanno i seguenti casi particolari: • • • per a > 0 la parabola ha la concavità rivolta verso l’alto, mentre per a < 0 la concavità è verso il basso (figura PRE-2.5); per b = 0 e c = 0 la parabola y = ax2 ha il vertice che coincide con l’origine degli assi (figura PRE-2.6); per b = 0 l’ascissa del vertice è nulla e quindi l’asse di simmetria della parabola coincide con l’asse y (figura PRE-2.7). a a = 2b 8 6 4 2 Figura PRE-2.8 Grandezze direttamente proporzionali. 0 1 2 3 4 b G. Conte, M. Ceserani, E. Impallomeni, Elettronica ed elettrotecnica, Vol. 1, Nuova Edizione OPENSCHOOL, © Ulrico Hoepli Editore S.p.A. 2015 6 Prerequisiti Grandezze direttamente proporzionali Due grandezze a e b sono direttamente proporzionali quando all’aumentare dell’una aumenta proporzionalmente anche l’altra e, quindi, il loro rapporto rimane costante: a ––– = k b Rappresentando le grandezze su un piano cartesiano si ottiene la retta a = kb (figura PRE-2.8), dove k è il coefficiente angolare della retta. Nella figura è stato posto k = 2 e quindi si ha sempre a = 2b. Grandezze inversamente proporzionali Due grandezze a e b sono inversamente proporzionali quando all’aumentare dell’una diminuisce l’altra, in modo che il loro prodotto rimanga costante: ab = k La curva che rappresenta questa legge è detta iperbole equilatera; la figura PRE-2.9 rappresenta l’andamento di a = f(b) nel caso a = 12/b e quindi ab = 12. a 12 ab = 12 a = 12 ––– b 6 4 3 2 1 0 1 2 3 4 6 12 b Figura PRE-2.9 Grandezze inversamente proporzionali. G. Conte, M. Ceserani, E. Impallomeni, Elettronica ed elettrotecnica, Vol. 1, Nuova Edizione OPENSCHOOL, © Ulrico Hoepli Editore S.p.A. 2015 7 Modulo A • Grandezze elettriche, bipoli, reti lineari in corrente continua Prerequisiti SCHEDA PRE-3 Risoluzione di un sistema di equazioni lineari Sistema di equazioni lineari Un’equazione nelle n incognite x1, x2, …, xn, si dice di 1° grado o lineare quando può essere ridotta alla forma seguente, in cui tutte le incognite compaiono alla prima potenza: a1 x1 + a2 x2 + + an xn = h dove a1, a2, …, an sono dei numeri reali noti, detti coefficienti delle incognite, e h è il termine noto, anch’esso di tipo reale. L’equazione è omogenea se h = 0, non omogenea in caso contrario. Considerando un insieme di n equazioni nelle n incognite indicate, si ottiene un sistema di equazioni lineari: ⎧a11 x1 + a12 x2 + + a1n xn = h1 ⎪a x + a x + + a x = h ⎪ 21 1 22 2 2n n 2 ⎨ .......................................... . ...... ⎪ ⎪⎩an1 x1 + an 2 x2 + + ann xn = hn Si chiama soluzione del sistema un gruppo ordinato di n numeri che, sostituiti alle n incognite, soddisfano tutte le equazioni del sistema. Nel seguito, limitandosi a un massimo di tre equazioni, le incognite verranno indicate con i simboli x, y, z. Metodo di confronto Il metodo di confronto è adatto ai sistemi di due equazioni e si applica usando la seguente procedura: 1. si ricava dalle due equazioni la stessa incognita, ponendo ogni equazione nella forma x = …, oppure y = …; 2. si uguagliano i secondi membri, ottenendo un’equazione in una sola incognita; 3. si risolve l’equazione, ricavando il valore dell’incognita; 4. si sostituisce il valore in una delle equazioni e si ricava l’altra incognita. Per chiarire la procedura, si segua la risoluzione del seguente sistema: ⎧ 5 x + 2 y = 18 ⎨ ⎩x = 4y Procedendo nel modo indicato si ottiene: 18 − 2 y ⎧ ⎪x = 5 ⎨ ⎪⎩ x = 4 y 22 y = 18 18 − 2 y = 4y 5 y= 18 22 18 − 2 y = 20 y y= 9 11 G. Conte, M. Ceserani, E. Impallomeni, Elettronica ed elettrotecnica, Vol. 1, Nuova Edizione OPENSCHOOL, © Ulrico Hoepli Editore S.p.A. 2015 Prerequisiti x=4 9 11 x= 36 11 Metodo di sostituzione Le operazioni da seguire per applicare il metodo di sostituzione sono le seguenti: 1. si ricava da un’equazione una delle incognite, ottenendo un’espressione in funzione delle altre incognite; 2. si sostituisce l’espressione in tutte le restanti equazioni, ottenendo n – 1 equazioni in n – 1 incognite; 3. per questo sistema ridotto si ripetono le operazioni 1 e 2, fino a ottenere una sola equazione in una incognita; 4. si risolve l’equazione e si ricava il valore dell’incognita; 5. rifacendo a ritroso il cammino percorso, si calcolano le altre incognite. Per chiarire la procedura si segua la risoluzione del seguente sistema: ⎧ y = 20 − 2 x − 3z ⎪ ⎨ x + 4 ( 20 − 2 x − 3z ) − 2 z = 3 ⎪ 3x + 5 ( 20 − 2 x − 3z + 4 z = 38 ) ⎩ ⎧ 2 x + y + 3z = 20 ⎪ ⎨ x + 4 y – 2z = 3 ⎪ 3x + 5 y + 4 z = 38 ⎩ ⎧................................................. ⎪ ⎨ x + 80 − 8 x − 12 z − 2 z = 3 ⎪ 3x + 100 − 10 x − 15 z + 4 z = 38 ⎩ ⎧.................... ⎪ ⎨ 7 x + 14 z = 77 ⎪ 7 x + 11z = 62 ⎩ ⎧ ⎪................... ⎪ 77 − 14 z ⎪ ⎨x = 7 ⎪ ⎪ 77 − 14 z + 11z = 62 ⎪⎩ 7 7 z= x= ⎧.......................... ⎪ ⎨ −7 x − 14 z = −77 ⎪ −7 x − 11z = −62 ⎩ 15 3 z=5 77 − 14 × 5 77 − 70 = 7 7 y = 20 − 2 × 1 − 3 × 5 ⎧................. ⎪ ⎨................. ⎪ −3z = −15 ⎩ x =1 y=3 Metodo di riduzione Nel caso di sistemi con due equazioni la procedura da seguire per applicare questo metodo è la seguente: 1. si moltiplica ogni equazione per un numero reale diverso da zero, in modo che i coefficienti di una incognita (per esempio x) risultino opposti nelle due equazioni; 2. si sommano membro a membro le due equazioni, in modo da ottenere una terza equazione, combinazione lineare delle due iniziali, in una sola incognita (y, nell’esempio); G. Conte, M. Ceserani, E. Impallomeni, Elettronica ed elettrotecnica, Vol. 1, Nuova Edizione OPENSCHOOL, © Ulrico Hoepli Editore S.p.A. 2015 8 9 Modulo A • Grandezze elettriche, bipoli, reti lineari in corrente continua 3. si risolve l’equazione ottenuta, determinando il valore di un’incognita; 4. si sostituisce tale valore in una delle equazioni iniziali e, risolvendola, si ottiene il valore dell’altra incognita. Per maggiori chiarimenti si consideri l’esempio seguente: ⎧6 x − 7 y = 1 ⎨ ⎩ 4 x − 2 y = 10 I coefficienti di x, 6 e 4, hanno minimo comune multiplo pari a 12, per cui, moltiplicando la prima equazione per 2 e la seconda per – 3 e sommando membro a membro, si ottiene: +12 x − 14 y = 2 −12 x + 6 y = −30 8 y = 28 / / − 8 y = −28 4x − 2 7 = 10 2 4 x − 7 = 10 y= x= 7 2 17 4 Metodo di Cramer Quello di Cramer è un metodo applicabile a sistemi lineari con un qualsiasi numero di equazioni e fa uso dei concetti di matrice e determinante. Dato che tali concetti esulano dai limiti del testo, ci si limiterà a riportare le formule risolutive valide per un sistema di due equazioni, scritto nella forma: ⎧ a1 x + b1 y = c1 ⎨ ⎩ a2 x + b2 y = c2 La soluzione del sistema è data da: x= b2 c1 − b1c2 a1b2 − a2 b1 y= a1c2 − a2 c1 a1b2 − a2 b1 valida quando è verificata la condizione: a1b2 − a2 b1 ≠ 0 Nel caso del sistema dell’esempio precedente, i coefficienti e i termini noti sono: a1 = 6 b1 = −7 c1 = 1 a2 = 4 b2 = −2 c2 = 10 e, quindi, essendo rispettata la condizione: a1b2 − a2b1 = 6 × ( −2 ) − 4 × ( −7 ) = −12 + 28 = 16 ≠ 0 le soluzioni del sistema sono date da: x= ( −2 ) × 1 − ( −7 ) × 10 16 y= = −2 + 70 68 = 16 16 6 × 10 − 4 × 1 60 − 4 56 = = 16 16 16 x= y= 7 2 G. Conte, M. Ceserani, E. Impallomeni, Elettronica ed elettrotecnica, Vol. 1, Nuova Edizione OPENSCHOOL, © Ulrico Hoepli Editore S.p.A. 2015 17 4