A.A. 2016/17
Marco Tarini - Università dell'Insubria
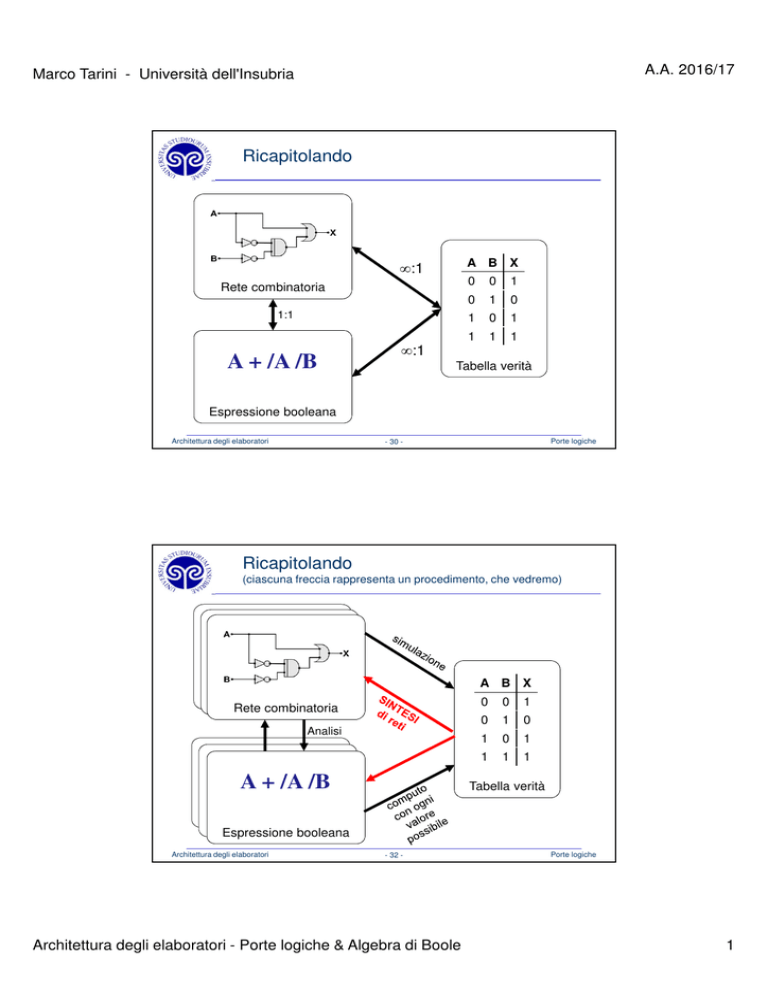
Ricapitolando
A B X
∞:1
Rete combinatoria
1:1
A + /A /B
0
0
1
0
1
0
1
0
1
1
1
1
∞:1
Tabella verità
Espressione booleana
Architettura degli elaboratori
Porte logiche
- 30 -
Ricapitolando
(ciascuna freccia rappresenta un procedimento, che vedremo)
A B X
Rete
combinatoria
Rete
Retecombinatoria
combinatoria
Analisi
A + /A /B
0
0
1
0
1
0
1
0
1
1
1
1
Tabella verità
Rete combinatoria
Rete combinatoria
Espressione booleana
Architettura degli elaboratori
- 32 -
Architettura degli elaboratori - Porte logiche & Algebra di Boole
Porte logiche
1
A.A. 2016/17
Marco Tarini - Università dell'Insubria
Regole di trasformazione
delle espressioni booleane
Regola
Prodotto logico (AND)
Somma logica (OR)
Elem. identità
1A=A
0+A=A
Elemento nullo
0A=0
1+A=1
Idempotenza
AA = A
A+A=A
Inverso
A /A = 0
A + /A = 1
Commutativa
AB=BA
A+B=B+A
Associativa
(A B) C = A (B C)
(A + B) + C = A + (B + C)
Distributiva
A + B C = (A + B) (A + C)
A (B + C) = A B + A C
Assorbimento
A (A + B) = A
A+AB=A
De Morgan
/(A B) = /A + /B
/(A + B) = /A /B
//A=A
Tertium non datur
Architettura degli elaboratori
- 36 -
Porte logiche
Proprietà degli operatori booleani: note
Le le regole di trasformazione (o «di riscrittura»)
ci consentono di passare da una espressione ad un’altra, equivalente.
l’equivalenza è garantita dalla teoria!
Obiettivo delle riscritture: ottimizzare l’espressione di partenza
Cioè: rendere il circuito associato piú economico, o piú veloce, etc
Gli A, B nelle regole rappresentano sotto-espressioni qualsiasi
(non necessariamente variabili: es: (A(B+C) + A(B+C)) = A(B+C)
Tutte le regole sono in doppia copia: una per l’AND una per l’OR
una è la regola DUALE dell’altra
cioè una è ottenuta dall’altra scambiando fra di loro:
AND <==> OR e 0 <==> 1
Ciascuna regola si può usare in un verso, o nel verso opposto
XXX = YYY
posso passare da XXX a YYY… oppure viceversa
Alcune regole somigliano a quelle dell’algebra numerica tradizionale
Altre sono piuttosto diverse (per esempio i due assorbimenti)!
Architettura degli elaboratori
- 37 -
Architettura degli elaboratori - Porte logiche & Algebra di Boole
Porte logiche
2
A.A. 2016/17
Marco Tarini - Università dell'Insubria
De Morgan explained
Nel primale:
/(A B) = /A + /B
cioè
A B =/ ( /A + /B )
«affermare che sia vero A e-anche B
signfica
negare che uno qualsiasi dei due sia falso»
Nel duale:
/(A + B) = /A /B
cioè
A + B = / ( /A /B )
«affermare che sia vero A oppure B (o entrambi)
signfica
negare che siano entrambi falsi»
Architettura degli elaboratori
- 38 -
Porte logiche
De Morgan: una conseguenza
DeMorgan ci mostra che possiamo, se lo vogliamo,
fare a meno di porte OR .
potremmo sempre sostituirle con porte AND (più alcuni NOT)
e viceversa!
ecco le leggi
di De Morgan…
…a circuito:
Architettura degli elaboratori
- 39 -
Architettura degli elaboratori - Porte logiche & Algebra di Boole
Porte logiche
3
A.A. 2016/17
Marco Tarini - Università dell'Insubria
Un altro assorbimento
A + /A B = A + B
Architettura degli elaboratori
A (/A + B) = AB
- 40 -
Porte logiche
Esempio di applicazione delle
regole di riscrittura
Si consideri la funzione booleana di 3 variabili G(a,b,c) espressa dalla
seguente equazione:
G(a,b,c) = (/a /b /c) + (/a /b c) + (/a /b c) + (/a b c) +(a /b c) + (a b c)
Semplificare l’espressione. Indicare le operazioni svolte
Espressione
Regola utilizzata
(ā b̄ c̄) + (ā b̄ c) + (ā b̄ c) + (ā b c) + (a b̄ c) + (a b c)
(ā b̄ c̄) + (ā b̄ c) + (ā b c) + (a b̄ c) + (a b c)
ā b̄ (c̄ +c) + ā c (b̄ +b) + a c (b̄ +b)
XY + XZ = X (Y + Z)
X + !X = 1 e X1=X
ā b̄ + ā c + a c
XY + XZ = X (Y + Z)
ā b̄ + c (ā + a)
X + !X = 1
ā b̄ + c
Architettura degli elaboratori
X+X=X
- 41 -
Architettura degli elaboratori - Porte logiche & Algebra di Boole
Porte logiche
4
A.A. 2016/17
Marco Tarini - Università dell'Insubria
Teorema del consenso
Dimostrazione
Architettura degli elaboratori
Porte logiche
- 42 -
Altri operatori booleani binari
(e porte corrispondenti)
Noi useremo circuiti che usano porte AND, OR e NOT
comodità, + uso diretto della logica classica
Altre porte popolari:
XOR
(«or esclusivo»)
A B X
0
0
0
0
1
1
1
0
1
1
1
0
Architettura degli elaboratori
uno o l’altro,
ma
NON entrambi
Significati intuitivi di A XOR B:
A oppure B, ma non entrambi
(in latino: A aut B)
vero se A e B diversi
falso se A e B uguali
vale /A se B = 1
vale A se B = 0
(e viceversa)
il contrario di A, se B vale;
A immutato, altrimenti
(e viceversa)
- 43 -
Architettura degli elaboratori - Porte logiche & Algebra di Boole
Porte logiche
5
A.A. 2016/17
Marco Tarini - Università dell'Insubria
Altri operatori booleani binari
(e porte corrispondenti)
Noi useremo circuiti che usano porte AND, OR e NOT
comodità, + uso diretto della logica classica
Altre porte popolari:
NXOR
(«fa il contrario di XOR»)
A B X
0
0
1
0
1
0
1
0
0
1
1
1
Architettura degli elaboratori
Significati intuitivi di A NXOR B:
uno XOR seguito da un NOT
A NXOR B = \( A XOR B)
cioè…
entrambi veri oppure
entrambi falsi
cioè…
AB + \A\B
cioè…
operatore di uguaglianza fra A e B:
vero se A e B sono uguali.
falso se sono diversi
Porte logiche
- 44 -
Altri operatori booleani binari
(e porte corrispondenti)
Noi useremo circuiti che usano porte AND, OR e NOT
comodità, + uso diretto della logica classica
Altre porte popolari:
NAND
(«fa il contrario di AND»)
NOR
(«fa il contrario di OR»)
A B X
A B X
0
0
1
0
0
1
0
1
1
0
1
0
1
0
1
1
0
0
1
1
0
1
1
0
Architettura degli elaboratori
- 45 -
Architettura degli elaboratori - Porte logiche & Algebra di Boole
Porte logiche
6
A.A. 2016/17
Marco Tarini - Università dell'Insubria
Porte NAND e porte NOR
Convenienti:
Sono le porte più economiche da realizzare (solo 2 transistor)
Hanno la latenza minore (vel maggiore) delle porte a 2 ingressi
Molto popolari!
Nota:
A NOR A = \A
B NAND B = \B
(verificare nella tabella!)
equivalenti
A
/A
A
/A
A
/A
quindi: con un NAND (o un NOR)
posso fare un NOT
Un NAND seguito da un NOT = AND
Un NOR seguito da un NOT = OR
Architettura degli elaboratori
- 46 -
Porte logiche
Porte NAND e porte NOR
Se ho a disposizione solo porte NAND…
(e quindi posso fare anche il NOT)
…allora posso fare anche l’AND , negando il risutato del NAND
A AND B = NOT (A NAND B)
NOT
A
B
AB
AND
(con due NAND!)
Architettura degli elaboratori
- 47 -
Architettura degli elaboratori - Porte logiche & Algebra di Boole
Porte logiche
7
A.A. 2016/17
Marco Tarini - Università dell'Insubria
Porte NAND e porte NOR
Se ho a disposizione solo porte NAND…
(e quindi posso fare anche il NOT e anche l’AND )
…allora posso fare anche l’OR , grazie a DeMorgan.
A AND B = NOT (A NAND B)
A
A+B
B
OR
(con tre NAND!)
Architettura degli elaboratori
- 48 -
Porte logiche
Operatori binari (porte logiche) universali
Vedremo che usando solo porte { AND, OR, NOT }
possiamo implementare a circuito qualsiasi funzione booleana data
(con qualsiasi numero di parametri) – v. forme canoniche, dopo
Ma, come abbiamo visto, grazie a De-Morgan:
con porte AND e NOT possiamo «fare» porte OR
(e viceversa, con OR e NOT possiamo «fare» porte AND)
Quindi, potremmo limitarci a porte AND e NOT e fare tutto con loro
(oppure OR e NOT )
Usando solo NAND possiamo fare NOT e AND
quindi possiamo fare tutto
Usando solo NOR possiamo fare NOT e OR
quindi possiamo fare tutto
per questo, NAND e NOR sono detti operatori universali
(sono gli unici due)
Architettura degli elaboratori
- 49 -
Architettura degli elaboratori - Porte logiche & Algebra di Boole
Porte logiche
8
A.A. 2016/17
Marco Tarini - Università dell'Insubria
Avvertenza
Per progettare un buon circuito (= ottimizzato)
che usa solo porte NAND (o solo NOR)
non ci si può limitare ad:
costruire un circuito ottimizzato con le porte NOT, AND e OR
(come vedremo nella prossima lezione)
sostiture queste con i circuiti visti che usano solo NAND.
Funzionerebbe, ma il risultato sarebbe molto lontano dall’ottimo!
Architettura degli elaboratori
- 50 -
Architettura degli elaboratori - Porte logiche & Algebra di Boole
Porte logiche
9