Successioni e serie
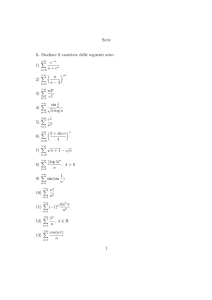
1. Calcolare i seguenti limiti di successioni:
√
√
1) lim
n+2− n−1
n→+∞
2)
lim 3n + 4n − 5n
n→+∞
2n+1 − 4n−1
n→+∞
3n
√
n
4) lim
n2
3)
lim
n→+∞
5)
(n3n+1 + n5 + 1)n!
n→+∞ (3n + 2n )(n + 1)!
lim
Ã
6)
7)
lim
n→+∞
n2 + n
n2 − n + 2
!n
lim [log(n + en ) − 3n]
n→+∞
2. Studiare il carattere delle seguenti serie:
1)
2)
+∞
X
e−n
n
n=0 n + e
+∞
X
µ
n=4
3)
n
n−3
¶n2
+∞
X
n2n
n
2
n=1 e
sin n1
√
4)
n log n
n=2
+∞
X
1
+∞
X
en
5)
2
n=1 n
6)
+∞
X
n=0
7)
+∞
X
µ
2 + sin n
4
√
n+1−
¶n
√
n
n=0
1
8)
9)
+∞
X
| log λ|n
, λ>0
n
n=1
+∞
X
1
sin(sin )
n
n=1
10)
11)
+∞
X
n!
n
n=1 n
+∞
X
(−1)n
n=1
12)
13)
sin2 n
n2
+∞
X
λn
, λ∈R
n=1 n
+∞
X
cos(nπ)
n
n=1
3. Stabilire per quali valori del parametro reale λ converge la serie
+∞
X
(λ2 −1)n .
n=0
Per i valori trovati calcolarne la somma.
4. Scrivere la successione delle somme parziali della serie
+∞
X
(λn+1 − λn ).
n=0
Determinarne il carattere e la somma.
5. Stabilire, al variare del parametro reale positivo λ, il carattere di
+∞
X
n=0
1
(2λ)n
+ nλ
+∞
X
6. Stabilire per quali valori del parametro reale a converge la serie
(n + 1 −
n=0
√
n2 + 2n)a .
7. Stabilire il carattere di
+∞
X
log n
.
2
n=2 n
8. Stabilire, al variare del parametro reale λ, il carattere di
+∞
X
n=1
9. Stabilire il carattere di
+∞
X
(−1)n
n=2
log n
.
n
2
√
n + log n
sin n.
n2 + λn
.
10. Stabilire il carattere di
cos( π2 n)
.
n
n=2
+∞
X
11. Dopo aver stabilito la convergenza delle seguenti serie, calcolarne la
somma:
1)
2)
3)
+∞
X
(−1)n
2n
n=0 2
+∞
X
2n
n+1
n=1 3
+∞
X
2n
2n
n=0 e
Traccia delle soluzioni.
n + 2 − (n − 1)
√
1. 1) = lim √
=0
n→+∞
n+2+ n−1
2) = lim −5n = −∞
n→+∞
3) = lim
4n (2 ·
n→+∞
4) = lim e
2 log n
n
n→+∞
³ ´n
2
4
3n
− 1)
= −∞
=1
(n3n+1 + n5 + 1)
n3n+1
=
lim
=3
n→+∞ (3n + 2n )(n + 1)
n→+∞ n3n
5) = lim
³
n log
6) = lim e
n2 +n
n2 −n+2
³
= lim e
n
´
n2 +n
−1
n2 −n+2
n→+∞
n→+∞
·
7) = lim n log(1 +
n→+∞
´
= e2
¸
n
) − 3 = −∞
en
µ
1
e−n
∼ 2
2. 1) Serie a termini positivi,
n
n+e
e
µ
2) Serie a termini positivi,
n
n−3
¶n2
¶n
, converge.
3n2
∼ e n−3 9 0, diverge.
Ã
n2n
2
3) Serie a termini positivi, n = n √
e
e2
3
!n
9 0, diverge.
sin 1
1
1
4) Serie e termini positivi, √ n ∼ 3
≤ 3 definitivamente (∀n ≥
n log n
n 2 log n
n2
3), converge.
1
en
1
5) Serie a termini positivi, 2 ∼ 2 , converge.
n
n
¶
µ
µ ¶n
2 + sin n n
3
6) Serie a termini positivi,
≤
, converge.
4
4
√
√
1
1
7) Serie a termini positivi, n + 1 − n = √
√ ∼ √ , diverge.
2 n
n+1+ n
s
| log λ|n
| log λ|
1
= √
→ | log λ|, quindi se < λ < e
n
n
n
e
1
converge per il criterio della radice; se λ = e, − diverge (è l’armonica), negli
e
altri casi la serie diverge per il criterio della radice.
1
1
1
9) Serie a termini positivi (N.B. 0 < sin < 1 ⇒ sin(sin ) > 0), sin(sin ) ∼
n
n
n
1
, diverge.
n
µ
¶
n + 1 −n
1
(n + 1)! n!
nn
→
10) Serie a termini positivi,
:
=
=
, la
(n + 1)n nn
(n + 1)n
n
e
serie converge per il criterio del rapporto.
¯
¯
2 ¯
¯
1
¯
n sin n ¯
11) Serie a termini di segno variabile, ¯¯(−1)
¯ ≤ 2 , converge assoluta2
n ¯
n
mente, quindi anche semplicemente.
8) Serie a termini positivi,
n
v¯
u
¯
¯ λn ¯
u
λn
¯
n ¯
12) Serie a termini di segno variabile,
→ 0 se e solo se |λ| ≤ 1; t
¯ ¯ =
¯
n
n¯
|λ|
√
→ |λ|, dunque, per il criterio della radice, se |λ| < 1 la serie converge
n
n
assolutamente e quindi anche semplicemente; se λ = 1 la serie diverge (è
l’armonica), se λ = −1 la serie converge per il criterio di Leibniz; se |λ| > 1 la
serie non converge perché il termine generale non tende a zero.
13) Serie a termini di segno variabile,
il criterio di Leibniz.
+∞
X
+∞
X (−1)n
cos(nπ)
=
, converge per
n
n
n=1
n=1
√
√
3. Serie geometrica, converge se |λ2 − 1| < 1, cioé per − 2 < λ < 2, λ 6= 0
1
e ha per somma
.
2 − λ2
4
4. Serie telescopica, Sn = λn+1 − 1; la serie converge se −1 < λ ≤ 1 e ha per
somma -1 se λ 6= 1, 1 se λ = 1; diverge se λ < 1; è irregolare se λ ≤ −1.
5. Serie a termini positivi, se λ >
1
1
1
,
∼
, converge; se λ ≤
n
λ
2 (2λ) + n
(2λ)n
1
1
1
,
∼ λ , diverge (serie armonica generalizzata) .
n
λ
2 (2λ) + n
n
√
√
6. Serie a termini positivi: Ãn + 1s≥ n2 + 2n.! n + 1 − n2 + 2n = n +
q
1
1
1
1 − (n + 1)2 − 1 = (n + 1) 1 − 1 −
∼
∼
, la serie
2
(n + 1)
2(n + 1)
2n
quindi converge se a > 1.
√
n n log n
7. Serie a termini positivi, poiché lim
= 0, definitivamente si ha
n→+∞
n2
√
n n log n
log n
1
che
≤ 1, cioè
≤ √ , la serie allora converge per il criterio
2
2
n
n
n n
del confronto.
¯√
¯
¯
¯√
¯ n + log n
¯
¯ n + log n ¯
1
¯
¯
¯
¯
8. Serie a termini di segno variabile, ¯¯ 2
sin n¯¯ ≤ ¯¯ 2
¯∼ 3,
n + λn
n + λn ¯ n 2
converge assolutamente, quindi anche semplicemente per ogni λ.
Ã
!
log n
1
9. Serie a termini di segno variabile. La serie diverge assolutamente
≥ se n ≥ 3 ;
n
n
log n
per studiare la convergenza semplice applichiamo il criterio di Leibniz,
è
n
log x
definitivamente decrescente, infatti la funzione y =
ha derivata negativa
x
per ogni x > e, quindi la serie converge semplicemente.
π
10. Serie a termini di segno variabile. Se n è pari, n = 2k, cos n = cos kπ =
2
+∞
+∞
X cos π n
X (−1)k
π
2
(−1)k ; se n è dispari cos n = 0. Dunque
=
; la serie
2
n
n=2
k=1 2k
converge per il criterio di Leibniz.
11. 1) Serie geometrica, =
+∞
X
µ
n=0
2) Serie geometrica, =
+∞
X
−1
4
¶n
µ ¶n
1
2
3 n=0 3
−
=
4
5
1
2
=
3
3
5
3) Serie geometrica, =
+∞
X
n=0
µ
2
e2
¶n
=
e2
e2 − 2
6