Un modello bayesiano non parametrico per tempi di attesa di eventi

POLITECNICO DI MILANO
SCUOLA DI INGEGNERIA INDUSTRIALE E
DELL’INFORMAZIONE
TESI DI LAUREA MAGISTRALE IN INGEGNERIA MATEMATICA
Un modello bayesiano non parametrico
per tempi di attesa di eventi ricorrenti
Relatore:
Prof.ssa Guglielmi Alessandra
Correlatore:
Prof.ssa De Iorio Maria
Anno Accademico 2014/2015
Candidato:
Marta Tallarita
Matricola 818291
2
Indice
Introduzione
11
1 Alcuni richiami di teoria sugli eventi ricorrenti
17
1.1
Notazione per i Recurrent Events . . . . . . . . . . . . . . . . 17
1.2
Metodi statistici basati sul conteggio di eventi . . . . . . . . . 19
1.3
Metodi statistici basati sui tempi di attesa . . . . . . . . . . . 21
1.3.1
Processi di rinnovo e modelli statistici per i tempi di
attesa . . . . . . . . . . . . . . . . . . . . . . . . . . . 21
1.3.2
Metodi statistici di analisi dei processi di rinnovo . . . 24
1.3.3
Generalizzazione dei modelli di rinnovo . . . . . . . . . 26
1.4
L’approccio bayesiano . . . . . . . . . . . . . . . . . . . . . . 28
1.5
L’approccio bayesiano non parametrico: Processo di Dirichlet . 30
1.5.1
1.6
Dirichelet Process Mixture . . . . . . . . . . . . . . . . 32
Metodi computazionali per il calcolo dell’inferenza bayesiana . 34
2 Modello
37
2.1
Notazione . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 40
2.2
Inferenza . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 41
3 Simulazioni
3.1
43
Dataset simulato 1 . . . . . . . . . . . . . . . . . . . . . . . . 45
3.1.1
Inferenza su m0 . . . . . . . . . . . . . . . . . . . . . . 48
3.1.2
Inferenza su m1 . . . . . . . . . . . . . . . . . . . . . . 49
3.1.3
Inferenza sul numero di cluster Kn . . . . . . . . . . . 50
3.1.4
Diagnostica di convergenza . . . . . . . . . . . . . . . . 50
3
4
INDICE
3.2
3.3
3.4
Dataset simulato 2 . . . . . . . . . . . . . . . . . . . . . . . . 52
3.2.1
Inferenza su m0 . . . . . . . . . . . . . . . . . . . . . . 55
3.2.2
Inferenza su m1 . . . . . . . . . . . . . . . . . . . . . . 56
3.2.3
Inferenza sul numero di cluster Kn . . . . . . . . . . . 56
3.2.4
Diagnostica di convergenza . . . . . . . . . . . . . . . . 57
Dataset simulato 3 . . . . . . . . . . . . . . . . . . . . . . . . 58
3.3.1
Inferenza su m0 . . . . . . . . . . . . . . . . . . . . . . 61
3.3.2
Inferenza su m1 . . . . . . . . . . . . . . . . . . . . . . 62
3.3.3
Inferenza sul numero di cluster Kn . . . . . . . . . . . 63
3.3.4
Diagnostica di convergenza . . . . . . . . . . . . . . . . 63
Confronto dei risultati . . . . . . . . . . . . . . . . . . . . . . 64
4 Analisi su dataset dei packages di R
65
4.1
Il modello bayesiano . . . . . . . . . . . . . . . . . . . . . . . 67
4.2
Analisi dei dati . . . . . . . . . . . . . . . . . . . . . . . . . . 69
4.3
Inferenza su mnew
0 ,
4.4
mnew
1 ,
Kn . . . . . . . . . . . . . . . . 70
4.3.1
Inferenza su m0 . . . . . . . . . . . . . . . . . . . . . . 71
4.3.2
Inferenza su m1 . . . . . . . . . . . . . . . . . . . . . . 72
4.3.3
Inferenza su K . . . . . . . . . . . . . . . . . . . . . . . 73
Inferenza sui parametri di regressione . . . . . . . . . . . . . . 74
4.4.1
Diagnostica di convergenza . . . . . . . . . . . . . . . . 74
4.4.2
Intervalli di credibilità a posteriori . . . . . . . . . . . 76
4.4.3
Confronto dei risultati . . . . . . . . . . . . . . . . . . 77
5 Analisi sui dati reali
81
5.1
Costruzione del Dataset . . . . . . . . . . . . . . . . . . . . . 81
5.2
Il modello bayesiano . . . . . . . . . . . . . . . . . . . . . . . 84
5.3
Analisi dei dati . . . . . . . . . . . . . . . . . . . . . . . . . . 88
5.4
Inferenza su mnew
0 ,
5.5
mnew
1 ,
Kn . . . . . . . . . . . . . . . . 90
5.4.1
Inferenza su m0 . . . . . . . . . . . . . . . . . . . . . . 90
5.4.2
Inferenza su m1 . . . . . . . . . . . . . . . . . . . . . . 91
5.4.3
Inferenza su K . . . . . . . . . . . . . . . . . . . . . . . 92
Inferenza su τ 2 e su σ . . . . . . . . . . . . . . . . . . . . . . . 93
INDICE
5.6
5.7
5
Inferenza sui parametri di regressione . . .
5.6.1 Diagnostica di convergenza . . . . .
5.6.2 Intervalli di credibilità a posteriori
Stochastic search variable selection per mi1
Bibliografia
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
95
95
97
106
108
6
INDICE
Elenco delle figure
1.1
Rappresentazione del processo di conteggio per dati basati su
eventi ricorrenti. . . . . . . . . . . . . . . . . . . . . . . . . . . 18
3.1
Istogramma degli intertempi simulati secondo le specifiche di
Simulazione 1 . . . . . . . . . . . . . . . . . . . . . . . . . . . 46
3.2
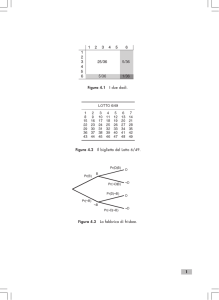
Tempi in cui si manifestano i primi 5 eventi in 9 pazienti scelti
in modo casuale . . . . . . . . . . . . . . . . . . . . . . . . . . 47
3.3
Densità a posteriori di m0 . . . . . . . . . . . . . . . . . . . . 48
3.4
Densità a posteriori di m1 . . . . . . . . . . . . . . . . . . . . 49
3.5
Densità a posteriori di Kn . . . . . . . . . . . . . . . . . . . . 50
3.6
Traceplot di σ . . . . . . . . . . . . . . . . . . . . . . . . . . . 51
3.7
ACF plot di σ . . . . . . . . . . . . . . . . . . . . . . . . . . . 51
3.8
Distribuzione degli αij : a sinistra scegliendo m0 = 1 e m1 =
0.3, a destra scegliendo m0 = −1 e m1 = −0.2 . . . . . . . . . 53
3.9
Istogramma degli intertempi simulati secondo le specifiche di
Simulazione 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . 54
3.10 Densità a posteriori di m0 . . . . . . . . . . . . . . . . . . . . 55
3.11 Densità a posteriori di m1 . . . . . . . . . . . . . . . . . . . . 56
3.12 Densità a posteriori di Kn . . . . . . . . . . . . . . . . . . . . 57
3.13 Istogramma degli intertempi simulati secondo le specifiche di
Simulazione 3 . . . . . . . . . . . . . . . . . . . . . . . . . . . 59
3.14 Distribuzione degli αij : a sinistra scegliendo m0 = 1 e m1 =
0.3, a destra scegliendo m0 = −1 e m1 = −0.2 . . . . . . . . . 60
3.15 Densità a posteriori di m0 . . . . . . . . . . . . . . . . . . . . 61
3.16 Densità a posteriori di m1 . . . . . . . . . . . . . . . . . . . . 62
7
8
ELENCO DELLE FIGURE
3.17 Densità a posteriori di Kn . . . . . . . . . . . . . . . . . . . . 63
4.1
4.2
4.3
4.4
4.5
4.6
4.7
4.8
4.9
Estratto dal dataset "readmission" . . . . . . . . . . . . .
Istogramma degli intertempi in scala logaritmica . . . . . .
Densità a posteriori di m0 ,con f (Wi1 , Wi2 , .., Wik ) = Wik .
Densità a posteriori di m1 ,con f (Wi1 , Wi2 , .., Wik ) = Wik .
Densità a posteriori di Kn ,con f (Wi1 , Wi2 , .., Wik ) = Wik .
ACF plot di β1 = chemo, β2 = sex, β3 = dukes . . . . . .
Trace plot di β1 = chemo, β2 = sex, β3 = dukes . . . . . .
Geweke plot di β1 = chemo, β2 = sex, β3 = dukes . . . .
Densità a posteriori di β1 = chemo, β2 = sex, β3 = dukes
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
66
69
71
72
73
74
75
75
76
5.1
5.2
5.3
5.4
5.5
5.6
5.7
5.8
5.9
5.10
5.11
5.12
5.13
5.14
5.15
5.16
5.17
5.18
Rappresentazione degli eventi per un generico paziente i . . . 82
Rappresentazione degli eventi per un generico paziente i . . . 83
Istogramma degli intertempi in scala logaritmica . . . . . . . . 88
Densità a posteriori di m0 ,con f (Wi1 , Wi2 , .., Wik ) = Wi1 +Wi2k+..+Wik 90
Densità a posteriori di m1 ,con f (Wi1 , Wi2 , .., Wik ) = Wi1 +Wi2k+..+Wik 91
Densità a posteriori di Kn ,con f (Wi1 , Wi2 , .., Wik ) = Wi1 +Wi2k+..+Wik 92
Densità a posteriori di σ . . . . . . . . . . . . . . . . . . . . . 93
Densità a posteriori di τ 2 . . . . . . . . . . . . . . . . . . . . . 94
ACF plot di β2 . . . . . . . . . . . . . . . . . . . . . . . . . . 96
Trace plot di β1 . . . . . . . . . . . . . . . . . . . . . . . . . . 96
Geweke plot di β4 . . . . . . . . . . . . . . . . . . . . . . . . . 97
Intervalli di credibilità marginali a posteriori per β1 . . . . . . 98
Densità a posteriori di β1 . . . . . . . . . . . . . . . . . . . . 99
Intervalli di credibilità marginali a posteriori per β2 . . . . . . 101
Intervalli di credibilità marginali a posteriori per β3 . . . . . . 103
Intervalli di credibilità marginali a posteriori per β4 . . . . . . 105
Densità a priori di m1 . . . . . . . . . . . . . . . . . . . . . . 107
Probabilità a posteriori di inclusione di m1 . . . . . . . . . . . 108
Elenco delle tabelle
4.1
4.2
Numero di pazienti con j intertempi, con j = 2,..,8 . . . . . . 67
Intervalli di credibilità marginali a posteriori per β1 , β2 , β3 . . 77
5.1
5.2
Numero di pazienti con j intertempi, con j = 2,..,9 . . . . .
P-value ottenuti dai test χ2 di indipendenza a coppie fra le
varie covariate . . . . . . . . . . . . . . . . . . . . . . . . . .
Intervalli di credibilità marginali a posteriori per β1 . . . . .
Intervalli di credibilità marginali a posteriori per β2 . . . . .
Intervalli di credibilità marginali a posteriori per β3 . . . . .
Intervalli di credibilità marginali a posteriori per β4 . . . . .
5.3
5.4
5.5
5.6
9
. 83
.
.
.
.
.
86
97
100
102
104
10
ELENCO DELLE TABELLE
Abstract
In questa tesi viene proposto un nuovo modello bayesiano non parametrico
per i tempi di attesa per eventi ricorrenti. La letteratura al riguardo è inesistente, quindi il modello proposto nell’elaborato sembra essere originale.
Componenti fondamentali per l’elaborazione di tale modello sono quindi da
una parte la teoria relativa agli eventi ricorrenti, dall’altra gli strumenti forniti dalla statistica bayesiana non parametrica.
Gli eventi ricorrenti sono dei processi nei quali gli eventi si ripetono più volte
nel corso del tempo; per descrivere questi eventi possono essere utilizzati metodi statistici basati sul conteggio di eventi oppure metodi statistici basati
sui tempi di attesa. In questo lavoro ci si è basati su questi ultimi metodi ed
in particolare sono stati molto utili i processi di rinnovo.
In questo elaborato è stato utilizzato l’approccio bayesiano non parametrico, in particolare è stato utilizzato il processo di Dirichlet come prior non
parametrica. Dopo aver descritto il modello che è stato utilizzato in tutta
la tesi, questo è stato in primo luogo testato su 3 differenti dataset simulati
per verificarne l’applicabilità, cioè per vedere se le stime bayesiane trovate
dal modello e dai codici fossero simili ai valori veri dei parametri fissati per
generare i dati simultati. Successivamente sono state svolte le analisi sul
dataset "readmission" presente in un package di R(fraitypack) ed infine il
modello è stato applicato a dati reali, che sono intertempi di pazienti affetti
da infezione ricorrente.
Per ognuno dei dataset a cui tale modello è stato applicato sono state riportate diverse inferenze: la distribuzione predittiva per le variabili latenti
del processo di Dirichlet e la distribuzione a posteriori del numero di cluster,
ossia del numero di gruppi che creano le variabili latenti.
11
12
Abstract
Le inferenze numeriche sono state calcolate utilizzando il linguaggio di programmazione JAGS che è in grado di costruire un algoritmo MCMC la cui
distribuzione invariante è la posterior dei parametri, date le osservazioni.
Introduzione
In questa tesi viene proposto un nuovo modello bayesiano non parametrico
per i tempi di attesa di eventi ricorrenti. La letteratura al riguardo è inesistente, quindi il modello proposto nell’elaborato sembra essere originale.
Il progetto è stato realizzato anche grazie alla collaborazione con l’University
College London, dove ho frequentato per un mese il Department of Statistics
che mi ha permesso di raccogliere i dati necessari per implementare il modello. Il lavoro di tesi è stato svolto sotto la supervisione della professoressa
Maria De Iorio di tale dipartimento, oltre alla prof.ssa Alessandra Guglielmi.
Componenti fondamentali per la costruzione di tale modello sono quindi da
una parte la teoria relativa agli eventi ricorrenti, dall’altra gli strumenti forniti dalla statistica bayesiana non parametrica, in particolare il processo di
Dirichlet (Ferguson, 1973).
Gli eventi ricorrenti sono dei processi nei quali gli eventi si ripetono più volte
nel corso del tempo. Se gli eventi di interesse si ripetono frequentemente
e sono incidentali, cioè la loro presenza non altera il processo stesso, allora per descrivere questi eventi vengono utilizzati metodi statistici basati sul
conteggio di eventi. Esempi di eventi incidentali sono le convulsioni epilettiche lievi o attacchi asmatici negli esseri umani. Eventi che possono ripetersi
frequentemente ma che non sono incidentali sono l’infarto miocardico e l’ictus. In questi ultimi esempi gli eventi possono alterare sostanzialmente la
condizione dell’individuo, influenzando così gli eventi futuri. Se, invece, gli
eventi sono relativamente rari, se si verifica un rinnovamento dell’individuo
dopo un evento, oppure se è di interesse la previsione del tempo per l’evento successivo, si utilizzano metodi statistici basati sui tempi di attesa. Tali
analisi sono utilizzate negli studi di fenomeni ricorrenti come infezioni, in cui
13
14
Introduzione
un individuo torna allo stato di buona salute una volta che l’infezione è stata
curata.
In questo lavoro l’approccio statistico seguito è stato quello di modellizzare i
tempi di attesa tra un evento e l’altro, ed in particolare sono stati molto utili
i processi di rinnovo. Per una trattazione completa sull’analisi degli eventi
ricorrenti, si veda Cook e Lawless, 2007.
Approcci NON bayesiani per modellizzare intertempi di eventi ricorrenti sono
trattati in Wang et al., 2001 e Prentice et al., 1981. Mentre per un esempio
di modello bayesiano nonparametrico, ma per dati NON ricorrenti, seppur in
contesto di analisi di sopravvivenza, si può consultare De Iorio et al., 2009.
In questo elaborato è stato utilizzato l’approccio bayesiano non parametrico. I modelli statistici parametrici sono modelli in cui il dato è rappresentato
da una variabile aleatoria con distribuzione di probabilità appartenente a
una data famiglia in corrispondenza biunivoca con un parametro vettoriale,
quindi di dimensione finita. I modelli non parametrici invece rilassano le assunzioni fatte sulle distribuzioni di probabilità delle osservazioni ma, anche
per modelli relativamente semplici, prevedono l’utilizzo di strumenti matematici più avanzati e complessi. Per i dettagli si veda Müller e Mitra, 2013.
In particolare, in questa tesi è stato utilizzato il processo di Dirichlet come
prior non parametrica.
Nel primo capitolo, quindi, dopo aver descritto gli eventi ricorrenti e i metodi
statistici con cui questi eventi possono essere descritti, mi sono concentrata
sulla statistica bayesiana e nello specifico sulla statistica bayesiana nonparametrica introducendo il processo di Dirichlet e le sue caratteristiche principali.
Dopo aver introdotto le fondamentali nozioni teoriche, nel Capitolo 2, è stato
descritto il modello che è poi stato utilizzato in tutta la tesi. Per ognuno dei
dataset a cui tale modello è stato applicato sono state riportate diverse inferenze: la distribuzione predittiva per le variabili latenti del processo di Dirichlet e la distribuzione a posteriori del numero di cluster, ossia del numero di
gruppi che creano le variabili latenti. Infatti, assumere che θi , i = 1, . . . , n
sia un campione da un processo di Dirichlet induce delle ties, quindi il numero di valori distinti θi , detto K, è una variabile aleatoria con una prior
Introduzione
15
distribution e una posterior distribution.
Le inferenze numeriche sono state calcolate utilizzando il linguaggio di programmazione JAGS che è in grado di costruire un algoritmo MCMC che
simula una catena markoviana la cui distribuzione invariante è la posterior
dei parametri, date le osservazioni.
In primo luogo, Capitolo3, tale modello è stato testato su 3 differenti dataset
simulati per verificarne l’applicabilità, cioè per vedere se le stime trovate per
le diverse simulazioni confermano le nostre aspettative. Ogni dataset è costituito da n=200 soggetti, e per ognuno sono stati considerati J=5 intertempi.
Il modello e il relativo codice sono stati in grado di riprodurre stime i cui
valori sono simili ai valori veri dei parametri fissati per generare i dati simultati: in tutti e tre i casi sia le distribuzioni marginali di G0 per un nuovo
paziente sia il numero di cluster sono come ci aspettavamo.
Nel capitolo successivo, invece, il nostro modello è stato testato sul dataset
"readmission" presente in un package di R (fraitypack). Tale dataset contiene i tempi di riospedalizzazione dei pazienti a cui è stato diagnosticato un
cancro al colon. I dati descrivono il tempo (in giorni) dei successivi ricoveri
dopo la data di intervento chirurgico; un totale di 861 eventi sono stati registrati per i 403 pazienti inclusi nell’analisi. Per ogni paziente è disponibile
un vettore di covariate x := (x1 , x2 , x3 , x4 ) con: x1 che indica se il paziente
ha ricevuto o meno la chemioterapia, x2 che indica il sesso, x3 che indica lo
stadio del tumore e x4 che è pari all’indice di comorbidità di Charlson. Anche
in questo caso sono state calcolate la distribuzione a posteriori per le variabili latenti del processo di Dirichlet e la distribuzione predittiva del numero
di cluster, ossia del numero di gruppi che creano le variabili latenti. Inoltre
sono stati calcolati gli intervalli di credibilità a posteriori dei coefficienti di
regressione in modo da comprendere in che modo le covariate influenzano la
variabile risposta. Questi risultati sono stati confrontati con le stime ottenute attraverso lo "Shared frailty model", contenuto nello stesso pacchetto da
cui sono stati presi i dati.
Infine, nell’ultimo capitolo, il modello è stato applicato al dataset fornito
da UCL, costituito da diversi pazienti a rischio di infezione urinarie. Ogni
soggetto effettua diversi controlli ospedalieri, ognuno dei quali è caratteriz-
16
Introduzione
zato da una variabile W BC che indica se il paziente è infetto (W BC > 0) o
meno (W BC = 0). Come prima cosa il dataset è stato manipolato in modo
tale che potesse essere applicato al nostro modello: sono stati identificati gli
eventi ricorrenti ed è stata introdotta la censura dove necessario.
Le covariate considerate per l’analisi sono inizialmente 5 e variano nel tempo: l’età del paziente e 4 covariate binarie che indicano la presenza o assenza
di certi sintomi ("urgenza", "dolore", "incontinenza da stress", "svuotamento"). Nel modello è cruciale come rappresentare la legge condizionale del
j-esimo intertempo (in scala logaritmica) in funzione dei precedenti intertempi. Lo facciamo attraverso un’intercetta al tempo j la cui distribuzione è
un Dirichlet process mixture model (Müller et al., 2015); la media di questo
parametro al tempo j dipende dai tempi precedenti linearmente attraverso
un funzione f (Wi1 , Wi2 , .., Wij−1 ).
Due sono state le scelte considerate in questa tesi:
• f (Wi1 , Wi2 , .., Wij−1 ) = Wij−1 , si genera quindi un processo markoviano in cui l’intertempo Wij dipende esclusivamente dall’intertempo
precedente Wij−1 ;
• f (Wi1 , Wi2 , .., Wij−1 ) = Wi1 +Wi2k+..+Wik , cioè l’intertempo Wij dipende
dalla media degli intertempi precedenti.
In particolare, ho monitorato la distribuzione predittiva di m0 new , dove m0 new
rappresenta la distribuzione della prima componente di G0 per un nuovo
paziente, la distribuzione predittiva di m1 new , dove, in modo analogo al caso
precedente, m1 new rappresenta la distribuzione della seconda componente di
G0 per un nuovo paziente, e la distribuzione a posteriori di Kn , cioè il numero
di valori distinti di (mi0 , mi1 ) del campione dal processo di Dirichlet G. Tale
valore indica il numero di cluster in cui è possibile raggruppare i valori distinti
(mi0 , mi1 ).
Successivamente ci si è concentrati sulle covariate: mostrando gli intervalli
di credibilità a posteriori per β1 , β2 , β3 , β4 e controllando la convergenza.
Infine è stata analizzata la significatività di mi1 utilizzando il metodo
Stochastic search variable selection prior (SSVS ).
Tutti i codici JAGS che producono le inferenze a posteriori, cioè la MCMC
Introduzione
17
la cui distribuzione limite è la posterior dei parametri, e tutti i file R per la
manipolazione dei dati e degli output di JAGS per costruire le inferenze a
posteriori e le predittive, sono stati scritti da me.
18
Introduzione
Capitolo 1
Alcuni richiami di teoria sugli
eventi ricorrenti
In questo capitolo introduciamo il concetto di eventi ricorrenti e i modi in cui
questi eventi possono essere descritti (metodi statistici basati sul conteggio
di eventi e metodi statistici basati sui tempi di attesa).
Inoltre, descriveremo le caratteristiche principali della statistica bayesiana e
quindi i metodi computazionali per il calcolo delle inferenze bayesiane.
La notazione e i risultati principali qui riportati sono quelli di Cook e Lawless,
2007.
1.1
Notazione per i Recurrent Events
Il mio lavoro si basa sull’analisi di eventi ricorrenti, ossia processi nei quali
gli eventi si ripetono più volte nel corso del tempo. La modellazione di eventi
ricorrenti può essere affrontata in vari modi.
Ai fini sia del modello che delle analisi statistiche, sono particolarmente utili i
concetti di funzione di intensità (intensity function) e di processo di conteggio
(counting process).
Partiamo per semplicità dal tempo t = 0 e poniamo 0 ≤ T1 < T2 < ...i tempi
in cui si verificano i diversi eventi, dove Tk è il tempo dell’evento k-esimo. Il
processo di conteggio associato {N (t), 0 ≤ t} registra il numero di eventi che
19
20CAPITOLO 1. ALCUNI RICHIAMI DI TEORIA SUGLI EVENTI RICORRENTI
P
si verificano durante l’intervallo di tempo [0, t], cioè N (t) = k=1 I(Tk ≤ t).
Più in generale, N (s, t) = N (t) − N (s) rappresenta il numero di eventi che
si verificano nell’intervallo (s, t]. In questo contesto, si noti che usiamo le
parentesi quadre e tonde per indicare, rispettivamente, se il punto finale di
un intervallo appartiene o meno all’intervallo stesso. Inoltre, utilizziamo t−
e t+ per denotare tempi che sono infinitesimamente più piccoli o più grandi
di t, rispettivamente. Per come sono stati qui definiti, i processi di conteggio
sono continui a destra; cioè, N (t) = N (t+ ).
La Figura 1.1 raffigura una realizzazione di un processo di conteggio per dati
basati su eventi ricorrenti.
Figura 1.1: Rappresentazione del processo di conteggio per dati basati su
eventi ricorrenti.
I modelli per eventi ricorrenti possono essere descritti in modo molto generale, considerando la distribuzione di probabilità per il numero di eventi che
si verificano in brevi intervalli [t, t + 4t), data la storia dell’evento ricorrente
prima del tempo t. Per impostare qualche notazione essenziale, definiamo
4N (t) = N (t + 4t− ) − N (t− ) che indica il numero di eventi nell’intervallo [t, t + 4t) , e indichiamo con H(t) = {N (s) : 0 ≤ s < t} la storia del
processo fino al tempo t. Per gli eventi che si verificano nel tempo continuo
facciamo l’ipotesi, matematicamente conveniente, che due eventi non possano verificarsi contemporaneamente. Quindi, la funzione di intensità fornisce
la probabilità istantanea, condizionata alla storia del processo, che un even-
1.2. METODI STATISTICI BASATI SUL CONTEGGIO DI EVENTI 21
to si verifichi in t e permette di definire il processo in termini matematici.
L’intensità è definita formalmente come
P (4N (t) = 1 | H(t))
4t→0
4t
λ(t | H(t)) = lim
(1.1)
La definizione (1.1) è molto generale e si può adattare ad ogni possibile dipendenza dell’intensità della storia del processo H(t).
Definiti i tempi degli eventi, si possono introdurre Wj := Tj − Tj−1 , j =
1, 2, 3, ...(T0 = 0), gli intertempi tra gli eventi (gap times).
Tipicamente, per descrivere e modellare il verificarsi degli eventi ricorrenti possiamo utilizzare due vie: attraverso il conteggio degli eventi oppure
attraverso l’analisi dei gap times tra gli eventi successivi. Questi metodi sono
discussi nei seguenti paragrafi. Talvolta è chiaro il metodo più appropriato
per un determinato problema, e in generale la scelta può essere guidata dalle
caratteristiche del processo sottostante, dagli obiettivi dell’analisi, o dai risultati del model checking. In molti contesti possono essere rilevanti le analisi
basate sia sul conteggio che sui tempi di attesa.
Due caratteristiche spesso interessanti del processo sono i trend temporali
e il clustering degli eventi. In linea di massima, un trend temporale in un
processo indica la tendenza del tasso di incidenza dell’evento, a cambiare nel
tempo in modo sistematico. Sono frequenti tendenze monotone, ma possono
verificarsi anche tendenze non monotone. Il clustering, invece, si riferisce alla
tendenza degli eventi a raggrupparsi.
1.2
Metodi statistici basati sul conteggio di eventi
Descriviamo ora brevemente metodi basati sul conteggio di eventi, per poi
concentrarci sui metodi basati sui gap times.
Modelli e metodi basati sul conteggio sono spesso utili quando gli eventi
di interesse si ripetono frequentemente, e gli eventi sono "incidentali", nel
senso che la loro presenza non altera il processo stesso. Esempi di eventi
22CAPITOLO 1. ALCUNI RICHIAMI DI TEORIA SUGLI EVENTI RICORRENTI
incidentali sono le convulsioni epilettiche lievi o attacchi asmatici negli esseri
umani. Eventi che possono ripetersi frequentemente ma che non sono incidentali sono l’infarto miocardico e l’ictus. In questi ultimi esempi gli eventi
possono alterare sostanzialmente la condizione dell’individuo, influenzando
così gli eventi futuri.
ll quadro canonico per l’analisi del conteggio degli eventi è il processo di
Poisson.
I modelli di Poisson in genere utilizzano l’età del processo come scala temporale. La proprietà degli incrementi indipendenti stabilisce che N (s1 , s2 ) è
indipendente da N (s3 , s4 ) purché s2 < s3 . Questo implica che per i processi
di Poisson la storia fino al tempo t non influenza la probabilità istantanea di
eventi al tempo t, e in assenza di covariate l’unico fattore che determina l’intensità è t. Processi di Poisson sono quindi processi di Markov, con funzione
intensità della forma
P (4N (t) = 1|H(t))
= ρ(t)
4t→0
4t
λ(t|H(t)) = lim
(1.2)
Oltre ad essere la funzione di intensità, ρ(t) è la rate function che dà la probabilità marginale (cioè non condizionata) istantanea di un evento al tempo
t. Cioè, ρ(t)4(t) = E[4N (t)], e se µ(t) indica il numero totale atteso di
eventi in [0, t], allora
Z
t
ρ(s) ds
µ(t) = E[N (t)] =
(1.3)
0
e ρ(t) = µ0 (t) = dµ(t)/dt.
Tale modello ( Equazione 1.2) può essere facilmente esteso per processi
in cui vi è variabilità del tasso di eventi tra i soggetti.
1.3. METODI STATISTICI BASATI SUI TEMPI DI ATTESA
1.3
23
Metodi statistici basati sui tempi di attesa
In questa sezione analizziamo i metodi basati sui tempi di attesa tra un evento
e il successivo (gap times) ed in particolare ci concentriamo sulla descrizione
dei processi di rinnovo.
Le analisi basate sui tempi di attesa sono spesso utili quando gli eventi sono
relativamente rari, quando si verifica un rinnovamento dell’individuo dopo un
evento, o quando è di interesse la previsione del tempo per l’evento successivo.
Tali analisi sono utilizzate negli studi di fenomeni ricorrenti come infezioni,
in cui un individuo torna allo stato di buona salute una volta che l’infezione
è stata curata.
I processi di rinnovo sono modelli standard per i tempi di attesa e sono
definiti come processi per i quali
λ(t|H(t)) = h(t − TN (t− ) )
(1.4)
Cioè, h(·) è la funzione di rischio per i tempi tra gli eventi, che sono indipendenti e identicamente distribuiti.
Sono spesso utili generalizzazioni di processi di rinnovo che comprendono
associazioni o tendenze tra i soggetti nei gap times. I processi di rinnovo e
le loro estensioni sono descritti nella sezione 1.3.1 e nella sezione 1.3.2.
1.3.1
Processi di rinnovo e modelli statistici per i tempi
di attesa
I processi di rinnovo sono quelli in cui gli intertempi Wj = Tj − Tj−1 , (j =
1, 2, ...) tra eventi successivi sono indipendenti e identicamente distribuiti.
Quando parliamo di indipendenza, si intende indipendenza condizionatamente ai "parametri", qualsiasi essi siano.
Questo è equivalente a richiedere che l’intensità sia della forma (1.4):
λ(t|H(t)) = h(B(t))
t > 0,
(1.5)
24CAPITOLO 1. ALCUNI RICHIAMI DI TEORIA SUGLI EVENTI RICORRENTI
dove B(t) = t − TN (t− ) è il tempo tra l’evento più recente prima di t e t stesso
, e h(w) è la funzione di rischio per le variabili Wj , cioè, se le Wj hanno
funzione di densità f (w) e funzione di sopravvivenza S(w) = P (W ≥ w),
allora
h(w) =
P (W < w + 4w|W ≥ w)
f (w)
= lim
.
S(w) 4w→0
4w
(1.6)
Si assume che l’origine del tempo t = 0 corrisponda al tempo del primo
evento. A volte questa ipotesi è rilassata e ad W1 è permesso di avere una
distribuzione diversa da W2 , W3 , ... , con i gap times ancora congiuntamente
indipendenti.
In un processo di rinnovo puro si può dire che non esista nessun trend, in
quanto i gap times sono i.i.d..
La distribuzione per i conteggi N (s, t) in processi di rinnovo è, in generale,
intrattabile dal punto di vista matematico. Un’eccezione è rappresentata per
il processo di rinnovo in cui le Wj sono variabili aleatorie esponenziali; il
processo è quindi un processo omogeneo di Poisson. Invece la distribuzione
di N (t), può essere ottenuta dalla relazione
P (N (t) ≥ n) = P (Tn ≤ t),
(1.7)
osservando che Tn = W1 +...+Wn è una somma di variabili casuali iid. Segue
anche dalla (1.7) che P (N (t) = n) = P (Tn ≤ t) − P (Tn+1 ≤ t), e
µ(t) = E[N (t)] =
∞
X
Fn (t)
(1.8)
n=1
dove Fn (t) è la funzione di ripartizione per Tn .
Le covariate possono essere incorporate nei processi di rinnovo in modi
semplici. Se a processi di rinnovo indipendenti sono associate delle covariate
fisse z allora imponiamo che la distribuzione comune dei gap times Wj di-
1.3. METODI STATISTICI BASATI SUI TEMPI DI ATTESA
25
penda da z. In tal caso, possono essere utilizzati modelli di regressione: le
due più importanti famiglie di tali modelli sono il proportional hazards model
in cui la funzione di rischio di Wj dato z è della forma
h(w|z) = h0 (w)exp(z 0 β)
(1.9)
e l’ accelerated failure time (AFT) model, in cui la funzione di rischio è del
tipo
0
h(w|z) = h0 (wez β )exp(z 0 β)
(1.10)
Sia nella (1.9) che nella (1.10), h0 (w) è una funzione a valori positivi denominata funzione di rischio "base".
Se ci sono covariate esterne z(t) variabili nel tempo, allora si possono considerare modelli di rinnovo in cui l’intensità è della forma
λ(t|H(t)) = h(B(t)|z(t))
t > 0,
(1.11)
Ciò equivale a incorporare le covariate dipendenti dal tempo z(t) nella funzione di rischio per la Wj . Il modello moltiplicativo con
h(w|z(t)) = h0 (w)exp(z 0 (t)β)
(1.12)
dove t = w+tN (t− ) , è molto utile. In un modello come (1.12) gli Wj sono indipendenti (data la storia delle covariate completa) ma non sono identicamente
distribuiti. Si noti, però, che in molte applicazioni l’assunzione di gap times
indipendenti non è sostenibile, anche dopo il condizionamento sulle covariate.
26CAPITOLO 1. ALCUNI RICHIAMI DI TEORIA SUGLI EVENTI RICORRENTI
1.3.2
Metodi statistici di analisi dei processi di rinnovo
Iniziamo con la descrizione dei metodi basati sui processi di rinnovo, per poi
quindi estendere tale metodo nelle sezioni successive.
Consideriamo ora n pazienti. Assumiamo per il momento che l’individuo
i sia osservato durante l’intervallo di tempo [0, τi ], che t = 0 corrisponda
all’inizio del processo e poniamo 0 ≤ Ti1 < Ti2 < ... < Tini ≤ τi i tempi in
cui si verificano i diversi eventi, dove Tik è il tempo dell’evento k-esimo per
il paziente i-esimo e ni corrisponde al numero degli eventi osservati per il
paziente i-esimo.
Definiti i tempi degli eventi, si possono introdurre Wij := Tij − Tij−1 , j =
1, 2, 3, ..ni , (Ti0 = 0) e Wini +1 = τi − Tini , gli intertempi tra gli eventi per il
paziente i, con i = 1, ...n. Si noti che l’ultimo tempo può essere censurato.
La funzione di intensità dell’evento è della forma (1.5); se consideriamo le
covariate fisse xi allora i gap times Wij tra gli eventi hanno funzione di rischio
h(w | xi ).
La funzione di verosimiglianza per m individui indipendenti è della forma
L=
"n
n
i
Y
Y
i=1
#
h(wij |xi ) exp(−H(wij |xi )) exp(−H(wi,ni +1 |xi ))
(1.13)
j=1
Rw
con H(w|x) = 0 h(u|x) du che è la funzione di rischio cumulativo per Wij ,
dato xi .
Se τi è un follow-up prespecificato o un tempo che è determinato indipendentemente dal processo dell’evento, allora la (1.13) è stato ottenuta calcolando
P (Wi1 = wi1 , ..., Wini = wini , Wini +1 > wini +1 ), dove per comodità usiamo
P (·) per indicare sia una probabilità che una densità di probabilità.
Siano f (w|x) = h(w|x)exp(−H(w|x)) e S(w|x) = exp(−H(w|x)) la densità e la funzione di sopravvivenza per Wij dato xi . Possiamo quindi riscrivere
la verosimiglianza come
L=
"n
n
i
Y
Y
i=1
j=1
#
f (wij |xi ) S(wini +1 |xi )
(1.14)
1.3. METODI STATISTICI BASATI SUI TEMPI DI ATTESA
27
che è la funzione di verosimiglianza per un campione casuale che coinvolge tempi di attesa wij (j = 1, ..., ni ) e tempi censurati a destra wini +1 per
i = 1, ..., n.
Se wini +1 = 0, cioè, se l’osservazione termina dopo l’evento ni − esimo, il termine S(wini +1 |xi ) nella (1.14) scompare. Metodi di analisi di sopravvivenza
standard e relativo software possono quindi essere utilizzati per l’inferenza.
Vediamo alcuni modelli di analisi di sopravvivenza qui adottati al caso di
eventi ricorrenti:
• Possono essere utilizzate le distribuzioni parametriche quali Weibull,
log-normale, e la distribuzioni logistica. Quando sono presenti covariate fisse, possono essere usati corrispondenti accelerated failure time
models (AFT) . Un modello AFT per un tempo di risposta W è quello
per cui Y = log W ha una distribuzione della forma
Y = β0 + x0 β + σε
(1.15)
dove x = (x1 , ...., xk )0 è il vettore delle covariate, β = (β1 , ..., βk )0 è il
vettore dei coefficienti di regressione, σ > 0 è un parametro di scala e
ε è una variabile casuale la cui distribuzione è indipendente da x.
Questo modello gestisce facilmente i casi in cui i valori delle covariate
sono fissate all’ interno degli intertempi ma variano tra gli intertempi.
In questo caso il modello AFT assume per Yij = log Wij che la distribuzione di Yij dato xij può essere rappresentata come
Yij = β0 + x0ij β + σεij
(1.16)
dove i termini εij sono variabili aleatorie i.i.d..
Covariate che variano all’interno dei gap sono più difficili da gestire con
i modelli AFT, ma sono facilmente trattati dal modello di Cox.
28CAPITOLO 1. ALCUNI RICHIAMI DI TEORIA SUGLI EVENTI RICORRENTI
• Il modello moltiplicativo di Cox per gli hazard è quello per cui la funzione di rischio per Wij dato xij è della forma
h(w|xij ) = h0 (w)exp(x0ij β)
(1.17)
Nel caso frequentista, le stime dei parametri vengono calcolate con il
metodo di verosimiglianza parziale.
Questo modello si adatta anche a covariate variabili nel tempo: in
questo caso xij è sostituito dal xij (t) nella (1.17).
Come sottolineato, l’ipotesi che i gap times Wij siano indipendenti e identicamente distribuiti quando non sono presenti covariate è molto forte, ed è
importante fare dei controlli diagnostici in ogni situazione. Lo stesso vale per
i modelli di regressione come (1.16) e (1.17), dove sono presenti le covariate
xij .
1.3.3
Generalizzazione dei modelli di rinnovo
L’assunzione di indipendenza tra gli intertempi è irragionevole in molte situazioni: si possono considerare modelli più generali specificando la successione
di distribuzioni condizionali, cioè L(Wi1 , ...., Wini ) = L(Wi1 ) × L(Wi2 |Wi1 ) ×
· · · · ×L(Wini |Wi1 , ...Wini −1 ), dove
Fj (w|xij , wij−i ) = P (Wij ≤ w|xij , wij−1 )
j = 1, 2, ..
(1.18)
Qui wij−1 = (wi1 , ...., wij−1 )0 e xij è il vettore di covariate per l’individuo i
associato al gap time j − esimo. Questo modello consente vari tipi di dipendenza dell’evento j-esimo dalla storia precedente.
I modelli possono anche essere formulati con covariate che variano all’interno dei gap times tra gli eventi. Possono essere presi in considerazione
diversi modelli di questa forma, che comprendono naturalmente i modelli di
rinnovo della sezione precedente, come casi particolari. In questo paragrafo
ci concentreremo sull’analisi condizionata dei successivi gap times.
1.3. METODI STATISTICI BASATI SUI TEMPI DI ATTESA
29
Per modelli dominati la funzione di verosimiglianza per un insieme di n processi indipendenti è un’estensione della (1.14):
L=
"n
n
i
Y
Y
i=1
#
f (wij |zij ) Sni +1 (wi,ni +1 |zini +1 )
(1.19)
j=1
dove zij è il vettore che modella la dipendenza di Wij rispetto a xij e a wij−1 ,
e fj (w|zij ) e Sj (w|zij ) sono, rispettivamente, la densità e la funzione di so(j−1)
pravvivenza di Wij dato zij . Se zij non dipende da wi
allora il modello si
riduce ad un processo di rinnovo con gap times indipendenti ma non identicamente distribuiti.
L’analisi statistica si basa su modelli di regressione per tempi di sopravvivenza. Le due famiglie dominanti di tali modelli sono il proportional hazards
models e il modello AFT. Nel primo caso assumiamo una hazard function
(j−1)
della forma
per Wij dati xij e wi
(j−1)
hj (w|xij , wi
(j−1)
) = hj (w|x0j , w0
)exp(zij0 βj )
j = 1, 2, ...
(1.20)
Nel caso frequentista, la forma più comune di analisi basato sulla (1.20) è
l’analisi semiparametrica della sezione 1.3.2 (ii), in cui le funzioni di rischio
base h0j (w) sono trattate in modo non parametrico.
I modelli AFT analogamente alla (1.20) definiscono Yij = logWij e sono
della forma (1.16) con
Y = β0j + z0ij βj + σj εij
j = 1, 2, ...
(1.21)
dove εij sono variabili casuali i.i.d. con una distribuzione nota Gj (ε), per
ogni i.
30CAPITOLO 1. ALCUNI RICHIAMI DI TEORIA SUGLI EVENTI RICORRENTI
1.4
L’approccio bayesiano
In questa tesi seguiremo l’approccio bayesiano. Questo metodo è basato su
una filosofia di analisi dei dati alternativa a quella propria dell’approccio
classico.
La differenza sostanziale sta nel fatto che per l’approccio classico i parametri
θ sono delle costanti incognite mentre per il metodo bayesiano i parametri
sono aleatori e dunque è necessario assegnare una distribuzione per il vettore
dei parametri. Questa distribuzione è denominata legge a priori o prior (π(θ))
ed esprime ciò che è noto relativamente ai parametri prima che l’esperimento
venga condotto.
La scelta della prior è il punto più difficile e critico dell’approccio bayesiano
poiché è una scelta di tipo soggettivista, infatti, in generale, le informazioni
a priori non sono mai così precise da generare un’unica legge a priori per θ.
E’ necessario quindi scegliere tra le distribuzioni plausibili o approssimare la
vera prior. Esistono due soluzioni ragionevoli:
• mistura (combinazione lineare convessa) di distribuzioni coniugate.
Definizione 1.4.1. Una famiglia F di distribuzioni sullo spazio parametrico Θ si dice coniugata al modello se, per ogni prior π ∈ F la
corrispondente distribuzione finale π(·|x) ∈ F .
Le prior coniugate sono molto utili se la famiglia F è parametrica, perché in questo caso si aggiornano solo i parametri della distribuzione a
posteriori.
Il vantaggio di questo metodo è il fatto che una mistura di coniugate potrebbe rappresentare una combinazione delle opinioni di diversi
esperti.
• prior non informative.
In genere viene effettuata questa scelta quando a priori ho informazioni deboli o vaghe perché le prior non informative danno luogo a
distribuzioni a posteriori che dipendono prevalentemente dai dati.
1.4. L’APPROCCIO BAYESIANO
31
Il fondamento della statistica bayesiana è dato dal teorema di Bayes la
cui applicazione permette di tenere conto delle opinioni e conoscenze esistenti
a priori sul fenomeno che è oggetto di studio. Esso connette distribuzione
a priori, verosimiglianza e distribuzione a posteriori in un unica formula e
fornisce un metodo per modificare il livello di fiducia in una data ipotesi alla
luce di una nuova informazione.
Teorema 1.4.2 (di Bayes).
Siano:
• X|θ ∼ p(x|θ), dove p(x|θ) è la verosimiglianza del campione X (nel
caso parametrico),
• θ ∼ π(θ), dove π(θ) è la distribuzione a priori ,
Allora la legge a posteriori π(θ|x) è data da :
π(θ|x) =
p(x|θ)π(θ)
.
p(x)
(1.22)
La distribuzione p(x) indica la legge marginale del campione X
Z
p(x) =
p(x|θ)π(θ) dθ
(1.23)
Tutte le inferenze bayesiane si basano sulla distribuzione a posteriori. Ad
esempio, la stima dei parametri verrà fatta calcolando statistiche riassuntive
di π(θ|x) (media o mediana a posteriori), mentre stime intervallari saranno
costruite a partire dai quantili di π(θ|x).
32CAPITOLO 1. ALCUNI RICHIAMI DI TEORIA SUGLI EVENTI RICORRENTI
1.5
L’approccio bayesiano non parametrico: Processo di Dirichlet
I modelli statistici parametrici sono modelli utilizzati per fare inferenza su
osservazioni che si assume essere realizzazioni di una variabile aleatoria con
distribuzione di probabilità appartenente a una data famiglia in corrispondenza biunivoca con un numero finito di parametri. I modelli non parametrici
invece rilassano le assunzioni fatte sulle distribuzioni di probabilità delle osservazioni.
In questo paragrafo si sviluppa uno dei più importanti modelli bayesiani
non parametrici, ossia il processo di Dirichlet (DP). La notazione e i risultati
qui riportati sono quelli di Müller et al., 2015.
Esistono diversi modi per definire tale processo; la definizione originale è stata data da Ferguson, 1973, il quale ha introdotto il modello DP come una
prior sullo spazio della misura di probabilità. Esso può essere visto come una
generalizzazione infinito dimensionale della distribuzione di Dirichlet finito
dimensionale.
Definizione 1.5.1. Sia α = (α1 , α2 , . . . , αk ) con αi > 0 per i = 1, 2, . . . , k.
Pk
Il vettore aleatorio G = (G1 , G2 , . . . , Gk ),
i=1 Gi = 1 ha distribuzione
di Dirichelet di parametro α, se G = (G1 , G2 , . . . , Gk−1 ) è assolutamente
continuo rispetto la misura di Lebesgue su Rk−1 con densità
P
Γ( ki=1 αi )
αk−1 −1
g α1 −1 g2α2 −1 · · · gk−1
f (g1 , g2 , . . . , gk−1 ) =
Γ(α1 )Γ(α2 ) . . . Γ(αk ) 1
1−
k−1
X
!αk −1
gi
i=1
con 0 ≤ gi ≤ 1 ∀i, 0 ≤ g1 + g2 + · · · + gk−1 ≤ 1, 0 altrimenti. Scriveremo
P ∼ D(α).
Ora possiamo definire il processo di Dirichlet.
Definizione 1.5.2. Sia α una misura finita su (X, B (X)), M := α(X); sia
G0 (·) = α(·)/M. Un DP con parametri α è una misura di probabilità aleatoria
G definita su X che assegna probabilità G(B) ad ogni insieme misurabile B
in modo tale che per ogni partizione finita e misurabile {B1 , . . . , Bk } di X la
1.5. L’APPROCCIO BAYESIANO NON PARAMETRICO: PROCESSO DI DIRICHLET33
distribuzione congiunta del vettore (G(B1 ), . . . , G(Bk )) sia una distribuzione
di Dirichelet con parametri
(α(B1 ), . . . , α(Bk )).
Usando le condizioni di consistenza di Kolmogorov(1933), Ferguson(1973)
ha mostrato che tale processo esiste.
Tale processo in genere è indicato con DP (α) oppure con DP (M, G0 ), dove
il parametro M è chiamato parametro di precisione o di massa totale e il
prodotto α := M G0 indica la misura base del DP.
Una caratteristica importante del DP è la natura discreta di G, per questo
motivo G può essere riscritta come somma pesata di masse puntiformi:
G(·) =
∞
X
wk δmh (·)
h=1
dove w1 , w2 , . . . sono i pesi di probabilità e δx (·) indica la misura di Dirac in
x.
Il processo di Dirichlet ha tre importanti proprietà:
ind
1. il DP è coniugato alla prior su X. Siano y1 , . . . , yn |G ∼ G e G ∼
DP (α). Allora,
G|y1 , . . . , yn ∼ DP (α +
n
X
δyi ).
i=1
2. la distribuzione di un campione (y1 , y2 , ..., yn+1 ) da un processo di Dirichlet può essere descritta come segue:
y1 ∼ G0
n
M
G0 +
yn+1 |y1 , . . . , yn ∼
M +n
M +n
Pn
i=1 δyi
n
,
n = 1, 2, . . . , N.
Questa osservazione permette di campionare marginalmente (y1 , y2 , ..., yn+1 )
senza simulare traiettorie del processo di Dirichlet.
34CAPITOLO 1. ALCUNI RICHIAMI DI TEORIA SUGLI EVENTI RICORRENTI
3. Il processo di Dirichlet ha traiettorie discrete. Ciò risulta evidente dalla
costruzione di Sethuraman.
Sethuraman (1994) ha fornito una definizione costruttiva del processo di
Dirichlet. Questa costruzione, detta stick-breaking, dà una idea della struttura del processo e fornisce un modo semplice per simulare le sue traiettorie. Si
considerino due famiglie di variabili aleatorie indipendenti (vh )h≥1 e (mh )h≥1 .
Siano
ind
mh ∼ G0 ,
ind
vh ∼ Be(1, M )
e si definiscano
w1 = v1
..
.
Y
wh = vh (1 − vl ).
l<h
Allora
G(·) =
∞
X
wk δmh (·)
h=1
definisce un processo di Dirichlet con parametri M, G0 .
1.5.1
Dirichelet Process Mixture
I processi di Dirichelet generano distribuzioni discrete, che sono poco utili
per la stima di densità continue. Questo limite può essere superato usando
misture di processi di Dirchelet ( modelli DPM).
Sia Θ lo spazio dei parametri. Per ogni θ ∈ Θ, sia fθ densità di probabilità
continua. Data una distribuzione di probabilità G definita su Θ , una mistura
di fθ su G ha la seguente densità:
Z
fG (y) =
fθ (y)dG(θ)
(1.24)
1.5. L’APPROCCIO BAYESIANO NON PARAMETRICO: PROCESSO DI DIRICHLET35
ind
Se consideriamo questo modello mistura(2.6) e assumiamo che yi |G ∼
FG , con G ∼ DP (M, G0 ) allora possiamo riscriverlo in modo equivalente
attraverso un modello gerarchico che introduce le variabili latenti θi :
ind
yi |θi ∼ fθi
ind
θi |G ∼ G
(1.25)
G ∼ DP (M, G0 )
Utilizzando questa formulazione (2.4), si nota che assumere che θi , i =
1, . . . , n sia un campione da un processo di Dirichlet induce delle ties, quindi
il numero di valori distinti θi , detto K, è una variabile aleatoria con una prior
distribution e una posterior distribution. Questo numero indica il numero di
cluster, ossia in numero di gruppi che creano le variabili latenti θi .
36CAPITOLO 1. ALCUNI RICHIAMI DI TEORIA SUGLI EVENTI RICORRENTI
1.6
Metodi computazionali per il calcolo dell’inferenza bayesiana
Nella maggior parte dei casi è molto complicato o addirittura impossibile
ricavare analiticamente la distribuzione a posteriori, e quindi si può ricorrere
a simulazioni numeriche.
Nella mia tesi ho usato metodi Markov Chain Monte Carlo (MCMC);
queste tecniche permettono di valutare numericamente la densità a posteriori, anche in casi molto complicati in cui, per esempio, la likelihood è ottenuta
attraverso simulazioni numeriche, la dimensione dello spazio dei parametri è
grande e la posterior ha una struttura complessa.
Tipicamente si è interessati a trovare il valore atteso, di una certa funzione reale del parametro θ, cioè h(θ) :
Z
Eπ [h(θ)|x] =
h(θ)π(θ|x) dθ.
(1.26)
Θ
Spesso quindi ci si ritrova a dover fare i conti con gli integrali e calcolarli analiticamente non è sempre agevole o addirittura possibile. E’ chiara l’esigenza
di trovare soluzioni alternative: un generico integrale può essere adeguatamente stimato tramite simulazione.
Simulo una catena di Markov {θm , m ≥ 0} (con Θ spazio degli stati) che sia
Harris-ergodica ed abbia misura limite pari a π, cioè simulo una catena di
Markov che sia:
• Irriducibile:
Definizione 1.6.1 (Catena di Markov irriducibile, spazio degli stati continuo). Sia Φ una misura di probabilità sullo spazio degli stati
Θ. Una catena di Markov con nucleo di transizione K(θ, A) è detta Φ-irriducibile, se ∀A ∈ B (Θ) tale che Φ(A) > 0 esiste n tale che
K n (θ, A) > 0, ∀θ ∈ Θ
• Harris-Ricorrente:
1.6.
METODI COMPUTAZIONALI PER IL CALCOLO DELL’INFERENZA BAYESIANA37
Definizione 1.6.2 (Catena di Markov Harris-Ricorrente). Consideriamo una catena di Markov (θm , m ≥ 0) con distribuzione di irriducibilità nominale Φ. Allora (θm , m ≥ 0) è Harris-ricorrente, se ∀A ∈ Θ
tale che Φ(A) > 0: P (θm ∈ A i.o.) = 1, ∀θ ∈ A
• Aperiodica, ossia che il periodo della catena sia pari a 1.
Allora uno stimatore non distorto di h(θ) sarà
m
Eπ [h(θ)|x] = h̄m =
1 X
h(θi )
m + 1 i=0
(1.27)
e π(θ|x) è la distribuzione invariante della catena di markov.
La consistenza di tale risultato è garantita dal teorema ergodico, noto
anche come legge dei grandi numeri per le catene di Markov:
Teorema 1.6.3 (teorema ergodico / legge dei grandi numeri per le catene
di Markov). Sia (θm , m ≥ 0) una catena di Markov irriducibile e Harrisricorrente su Θ con distribuzione invariante π. Si consideri una funzione h
R
π-misurabile tale che Θ |h(θ)|dπ(θ) < ∞. Allora
m
1 X
h(θi ) =
lim
m→∞ m + 1
i=0
Z
h(θ)dπ(θ) ≡ Eπ h(θ)
Θ
Teorema 1.6.4. Una catena di Markov (θm , m ≥ 0) definita su Θ con
distribuzione invariante π e matrice di transizione K è Harris-ergodica ⇔
n→∞
||K n (θ, ·) − π(·)|| −→ 0
∀θ ∈ Θ
Per maggiori dettagli si veda Jackman, 2009
38CAPITOLO 1. ALCUNI RICHIAMI DI TEORIA SUGLI EVENTI RICORRENTI
Capitolo 2
Modello
Riprendendo la notazione introdotta nel capitolo precedente, denotiamo con
Wij , j = 1, 2, 3, . . . i gap times tra i vari eventi per il paziente i, i =
1, 2, 3, . . . n. Assumiamo che ogni individuo i sia osservato nell’intervallo
[0,τi ] e che t = 0 corrisponda al primo evento. Con xij definiamo il vettore
di covariate al tempo j.
Se ni eventi sono osservati ai tempi 0 < Ti1 < · · · < Tini ≤ τi , poniamo
wij = Tij − Tij−1 per j = 1, . . . , ni e wini +1 = τi − Tini , dove Ti0 = 0. Questi
sono i gap times osservati per il paziente i, con l’ultimo tempo che può essere
censurato.
Indichiamo con J il numero massimo, fra i vari individui, di eventi ripetuti,
cioè J = maxi=1,...,n (ni ).
39
40
CAPITOLO 2. MODELLO
Il modello che utilizzeremo in tutta la tesi è il seguente: ∀i = 1, · · · n
Yi1 =: logWi1 = xi β1 + σεij
Yij =: logWij = xi βj + αij + σεij
∀j = 2, · · · ni
(2.1)
(2.2)
ind
εij ∼ N (0, 1).
dove
Condizionatamente ai parametri, i vari Yi =: (Yi1 , ..., Yini ) sono indipendenti; il vettore dei parametri è θ = (β, σ, (α1 , ..., αn )), con αi = (αi1 , .., αini ).
Quindi stiamo assumendo che gli intertempi abbiano distribuzione gaussiana:
Yi1 |β1 , σ ∼ N (xi β1 , σ 2 )
Yij |Yi1 , .., Yij−1 , βj , σ, αij ∼ N (xi βj + αij , σ 2 )
Per quanto riguarda la prior assumiamo che i blocchi (in θ) β, σ, (α1 , ..., αm )
siano indipendenti e che abbiano le seguenti distribuzioni:
σ ∼ U (0, σ0 ),
σ0 > 0,
 

0
 . 

2 
.
β ∼N
 .  , (β0 ) I  ,
0
ind
αij | mi0 , mi1 , τ ∼ N (mi0 + mi1 logf (...), τ 2 )
iid
mi0 , mi1 | G ∼ G
G ∼ DP (M, G0 )
41
τ 2 ∼ inv-gamma(5, 1)
M ∼ U (0, 10)
G0 = N (0, 10) × L(Z)
dove Z = 2X − 1, con X ∼ Beta(3, 3)
Si noti che ora lo spazio parametrico è stato "aumentato", e quindi il parametro è θ = (β, σ, (α1 , ..., αn ), (m1 , ..., mn ), τ02 , M ), con mi = (mi0 , mi1 ).
Inoltre osserviamo che:
• la seconda componente di G0 è limitata all’intervallo (-1,1) perchè altrimenti il processo diventerebbe non stazionario con varianza che tende
ad infinito;
• il vettore delle covariate xi nelle Equazione (2.1) e (2.2) può diventare
un vettore di covariate che varia nel tempo xij (t).
In questa tesi confronteremo tre possibili scelte per f :
• f (Wi1 , Wi2 , .., Wik ) = Wik
• f (Wi1 , Wi2 , .., Wik ) =
Wi1 +Wi2 +..+Wik
k
• f (Wi1 , Wi2 , .., Wik ) =
Wi1 ·Wi2 ·..·Wik
k
In base alla scelta di f si genera un diverso comportamento nel tempo; scegliendo f (Wi1 , Wi2 , .., Wik ) = Wik si genera un processo markoviano in cui
l’intertempo Wij dipende esclusivamente dall’intertempo precedente Wij−1 ,
∀j = 2, .., ni . Se, invece, f (Wi1 , Wi2 , .., Wik ) = Wi1 +Wi2k+..+Wik allora l’intertempo Wij dipende dalla media degli intertempi precedenti. Infine, se
f (Wi1 , Wi2 , .., Wik ) = Wi1 ·Wi2k ·..·Wik allora l’intertempo Wij dipende dal prodotto degli intertempi precedenti. Si noti che è necessario dividere per k
altrimenti il processo potrebbe esplodere.
E’ importante sottolineare il fatto che stiamo utilizzando una prior non
parametrica, cioè G che è un processo di Dirichlet.
42
2.1
CAPITOLO 2. MODELLO
Notazione
Uniformiamo la notazione utilizzata in questo paragrafo con quella utilizzata
nella Sezione 1.5. Abbiamo quindi che le variabili yi presenti nel Capitolo
1 corrispondono al vettore αi presente nel modello, mentre le le variabili θi
corrispondono al vettore mi .
2.2. INFERENZA
2.2
43
Inferenza
Le inferenze che riportiamo per ognuno dei dataset sono:
• la distribuzione a posteriori di m0 new , dove m0 new rappresenta la distribuzione della prima componente di G0 per un nuovo paziente:
π(m0 new | dati) =
R
=
L(m0 new , m10 , ...mn0 )
=
L(m10 , ...mn0 )
L(m0 new , m10 , ...mn0 | G) · π(dG)
=
L(m10 , ...mn0 )
Z
G0 · π(dG | m10 , ...mn0 ),
(2.3)
con G0 =
P∞
l=1
wl δτ0l ,
ind
τ0l ∼ G00
• la distribuzione a posteriori di m1 new , dove, in modo analogo al caso precedente, m1 new rappresenta la distribuzione della seconda componente
di G0 per un nuovo paziente:
π(m1 new | dati) =
R
=
L(m1 new , m11 , ...mn1 )
=
L(m11 , ...mn1 )
L(m1 new , m11 , ...mn1 | G) · π(dG)
=
L(m11 , ...mn1 )
Z
G · π(dG | m11 , ...mn1 )
(2.4)
con G1 =
P∞
l=1
wl δτ1l ,
ind
τ1l ∼ G01
• la distribuzione a posteriori di Kn , cioè il numero di valori distinti
di (mi0 , mi1 ) del campione dal processo di Dirichlet G. Tale valore
indica il numero di cluster in cui è possibile raggruppare i valori distinti
(mi0 , mi1 ).
Le inferenze numeriche sono state calcolate utilizzando il linguaggio di programmazione JAGS (Plummer et al., 2003), in modo da richiamarlo tramite
un interfaccia di R. Il programma è in grado di costruire un algoritmo MCMC
la cui distribuzione invariante è la posterior di θ, date le osservazioni. Due
44
CAPITOLO 2. MODELLO
aspetti da tenere in considerazione sono il periodo di burn-in e la correlazione tra punti. Infatti all’inizio del campionamento la distribuzione generata
dall’algoritmo MCMC potrebbe essere significativamente lontana dalla distribuzione target ( cioè la distribuzione a posteriori dei parametri del modello),
quindi l’output MCMC è in genere suddiviso in due parti: un periodo iniziale di burn-in, che viene scartato e la restante parte della catena che, invece,
rappresenta accuratamente la distribuzione desiderata. Inoltre, un algoritmo
MCMC genera catene di Markov di campioni ognuno dei quali è correlato
a quello generato precedentemente e successivamente a lui. Pertanto se si
è interessati a campioni indipendenti vanno considerati soltanto i campioni
generati ogni n (thinning= n).
Capitolo 3
Simulazioni
Per verificare l’applicabilità del modello proposto nella sezione precedente, si
è condotta un’analisi su dati simulati.
Considerando il modello introdotto nel Capitolo 2, nel primo dataset poniamo αij = 0 ∀i = 1, ..., n, ∀j = 1, ..., J , nel secondo imponiamo pari a
0 i coefficienti βj , ∀j = 1, ..., J ed infine, per la terza simulazione, consideriamo sia i coefficienti αij ∀i = 1, ..., n, ∀j = 1, ..., J che i coefficienti
βj , ∀j = 1, ..., J diversi da 0.
I parametri utilizzati in tutto il capitolo sono:
• σ0 = 10
• β02 = 1000
Per tutte le simulazioni di questo capitolo, tramite JAGS, sono state eseguite
10.000 iterazioni di burn-inn, con thinning pari a 50, per un final sample size
di 5.000 iterazioni.
Come descritto nel capitolo precedente, varie sono le possibili scelte per
f (Wi1 , Wi2 , .., Wik ):
• f (Wi1 , Wi2 , .., Wik ) = Wik
• f (Wi1 , Wi2 , .., Wik ) =
Wi1 +Wi2 +..+Wik
k
45
46
CAPITOLO 3. SIMULAZIONI
• f (Wi1 , Wi2 , .., Wik ) =
Wi1 ·Wi2 ·..·Wik
k
Per ognuna di queste riportiamo diverse inferenze:
• la distribuzione a posteriori di m0 new (Equazione 2.3)
• la distribuzione a posteriori di m1 new (Equazione 2.4)
• la distribuzione a posteriori di Kn , cioè il numero di valori distinti di
(mi0 , mi1 ) del campione dal processo di Dirichlet G
3.1. DATASET SIMULATO 1
3.1
47
Dataset simulato 1
I dati sono simulati dal modello precedente, in modo indipendente, scegliendo:
βj = 1 ∀j
σ=1
αij = 0 ∀ i, j
J =5
n = 200
iid
xi ∼ N (0, 1)
Quindi le variabili Yij sono state simulate da una gaussiana di media xi e
varianza pari a 1, ∀ i, j = 1, ..., J.
48
CAPITOLO 3. SIMULAZIONI
La Figura 2.1 riporta gli intertempi simulati in scala logaritmica per i
diversi pazienti.
Figura 3.1: Istogramma degli intertempi simulati secondo le specifiche di
Simulazione 1
3.1. DATASET SIMULATO 1
49
Il grafico in figura 2.2 mostra J=5 eventi per 9 soggetti scelti in modo
arbitrario.
Figura 3.2: Tempi in cui si manifestano i primi 5 eventi in 9 pazienti scelti
in modo casuale
Dal grafico si nota che, per i diversi pazienti, gli eventi si verificano in
modo arbitrario.
50
3.1.1
CAPITOLO 3. SIMULAZIONI
Inferenza su m0
I risultati ottenuti, al variare della funzione f ( f (Wi1 , Wi2 , .., Wik ) = Wik ,
f (Wi1 , Wi2 , .., Wik ) = Wi1 +Wi2k+..+Wik oppure f (Wi1 , Wi2 , .., Wik ) = Wi1 ·Wi2k ·..·Wik ),
sono sovrapponibili, quindi per semplicità riportiamo le inferenze solo per il
caso f (Wi1 , Wi2 , .., Wik ) = Wik .
Figura 3.3: Densità a posteriori di m0
Dalla Figura 3.3 si nota che, come ci aspettavamo, la distribuzione del parametro m0 per un nuovo paziente è concentrata sullo 0, questo poichè nel
modello simulato αij = 0 ∀i, j.
3.1. DATASET SIMULATO 1
3.1.2
51
Inferenza su m1
Anche in questo caso i risultati ottenuti, per le varie scelte della funzione f ,
sono identici.
Figura 3.4: Densità a posteriori di m1
Come per la distribuzione del parametro m0 , anche la distribuzione del
parametro m1 per un nuovo paziente è concentrata sullo 0, perchè nel modello
simulato αij = 0 ∀i, j.
52
3.1.3
CAPITOLO 3. SIMULAZIONI
Inferenza sul numero di cluster Kn
La scelta di f non risulta significativa neppure per l’inferenza sul numero dei
cluster. Come si evince dalla Figura 3.5 i pazienti appartengono ad un unico
gruppo con probabilità maggiore di 0.8.
Quindi, come per le distribuzioni marginali di G0 , questo risultato conferma
le nostre aspettative, infatti i dati sono stati simulati da un unico gruppo.
Figura 3.5: Densità a posteriori di Kn
3.1.4
Diagnostica di convergenza
Osservando i traceplot (Figura 3.6) e l’ autocorrelation plot (Figura 3.7) per
la variabile σ notiamo che la catena è giunta a convergenza; infatti i traceplot
sono molto fitti e l’ autocorrelazione è bassa.
3.1. DATASET SIMULATO 1
Figura 3.6: Traceplot di σ
Figura 3.7: ACF plot di σ
53
54
3.2
CAPITOLO 3. SIMULAZIONI
Dataset simulato 2
I dati sono simulati dal modello introdotto nel Capitolo 2, in modo indipendente, scegliendo:
βj = 0 ∀j
σ=1
αij ∼ N (m0i + m1i ∗ Yij−1 , 0.5) ∀i, j
Per 100 pazienti
m0i = 1 e m1i = 0.3
per gli altri 100 pazienti
m0i = −1 e m1i = −0.2
J =5
n = 200
iid
xi ∼ N (0, 1)
3.2. DATASET SIMULATO 2
55
Quindi le variabili Yij sono state simulate da una gaussiana di media αij e
varianza pari a 1, ∀ i, j = 1, ..., J mentre le variabili αij hanno distribuzione
gaussiana con media = m0i + m1i ∗ Yij−1 e varianza = 0.5, ∀i, j .
In questo caso, come si nota dalla Figura 3.8, ho simulato gli αij da due
gruppi differenti, quindi ci si aspetta che la distribuzione a posteriori di Kn
sia concentrata sul valore 2.
Figura 3.8: Distribuzione degli αij : a sinistra scegliendo m0 = 1 e m1 = 0.3,
a destra scegliendo m0 = −1 e m1 = −0.2
56
CAPITOLO 3. SIMULAZIONI
La Figura 3.9 riporta gli intertempi simulati in scala logaritmica per i
diversi pazienti.
Figura 3.9: Istogramma degli intertempi simulati secondo le specifiche di
Simulazione 2
Come per la prima simulazione, i risultati che otteniamo, variando la
funzione f , sono molto simili tra loro. Per semplicità riportiamo quindi i grafici relativi ad un’unica scelta di f , in particolare qui scegliamo
f (Wi1 , Wi2 , .., Wik ) = Wi1 ·Wi2k ·..·Wik .
3.2. DATASET SIMULATO 2
3.2.1
57
Inferenza su m0
Figura 3.10: Densità a posteriori di m0
Dalla Figura 3.11 si nota che, la distribuzione del parametro m0 per un
nuovo paziente è concentrata sui valori -1 ed 1.Tale risultato conferma le
nostre aspettative questo poichè 100 pazienti sono stati simulati scegliendo
m0 = 1 e gli altri 100 pazienti scegliendo m0 = −1.
58
3.2.2
CAPITOLO 3. SIMULAZIONI
Inferenza su m1
Figura 3.11: Densità a posteriori di m1
Si osserva che la densità a posteriori di m1 è concentrata sui valori 0.3 e -0.2,
questo perchè 100 pazienti sono stati simulati scegliendo m1 = 0.3 e gli altri
100 pazienti scegliendo m1 = −0.2.
3.2.3
Inferenza sul numero di cluster Kn
Anche l’inferenza sul numero dei cluster conferme le nostre aspettative, infatti
la densità a posteriori di Kn è concentrata sul 2.
3.2. DATASET SIMULATO 2
59
Figura 3.12: Densità a posteriori di Kn
3.2.4
Diagnostica di convergenza
I traceplot e le autocorrelazioni sono simili al dataset 1 e per tal motivo
non li riportiamo. Dunque non si può escludere che la catena sia giunta a
convergenza.
60
3.3
CAPITOLO 3. SIMULAZIONI
Dataset simulato 3
I dati sono simulati dal modello introdotto nel Capitolo 2, in modo indipendente, scegliendo:
βj = 1 ∀j
σ=1
αij ∼ N (m0i + m1i ∗ Yij−1 , 0.5) ∀i, j
Per 100 pazienti
m0i = 1 e m1i = 0.3
per gli altri 100 pazienti
m0i = −1 e m1i = −0.2
J =5
n = 200
iid
xi ∼ N (0, 1)
3.3. DATASET SIMULATO 3
61
Quindi le variabili Yij sono state simulate da una gaussiana di media
xi + αij e varianza pari a 1, ∀ i, j = 1, ..., J mentre le variabili αij hanno
distribuzione gaussiana con media = m0i + m1i ∗ Yij−1 e varianza = 0.5, ∀i, j.
In quest’ ultima simulazione i dati sono stati generati da due gruppi differenti, inoltre sono state introdotte anche le covariate xi .
La Figura 3.16 riporta gli intertempi simulati in scala logaritmica per i diversi
pazienti.
Figura 3.13: Istogramma degli intertempi simulati secondo le specifiche di
Simulazione 3
62
CAPITOLO 3. SIMULAZIONI
Scegliendo per il primo gruppo di pazienti m0 = 1 e m1 = 0.3 e per il
secondo gruppo m0 = −1 e m1 = −0.2 si ottengono i seguenti risultati per
la distribuzione di alpha:
Figura 3.14: Distribuzione degli αij : a sinistra scegliendo m0 = 1 e m1 = 0.3,
a destra scegliendo m0 = −1 e m1 = −0.2
Valgono le stesse considerazioni fatte per le due simulazioni precedenti
per quanto riguarda la scelta di f . In quest’ultimo caso riportiamo le analisi
ottenute con f (Wi1 , Wi2 , .., Wik ) = Wi1 +Wi2k+..+Wik .
3.3. DATASET SIMULATO 3
3.3.1
63
Inferenza su m0
Figura 3.15: Densità a posteriori di m0
In quest’ ultima analisi il dataset da cui sono state fatte le simulazione è più
complesso, le stime quindi risultano più difficili.
Nonostante ciò, osserviamo che la distribuzione del parametro m0 per un
nuovo paziente è costituita da due gobbe concentrate sui valori -1 ed 0.8(∼
1), questo poichè 100 pazienti sono stati simulati scegliendo m0 = 1 e gli altri
100 pazienti scegliendo m0 = −1.
64
3.3.2
CAPITOLO 3. SIMULAZIONI
Inferenza su m1
Figura 3.16: Densità a posteriori di m1
La densità a posteriori di m1 è concentrata sui valori 0.2 (∼ 0.3) e -0.2,
questo perchè 100 pazienti sono stati simulati scegliendo m1 = 0.3 e gli altri
100 pazienti scegliendo m1 = −0.2.
3.3. DATASET SIMULATO 3
3.3.3
65
Inferenza sul numero di cluster Kn
Figura 3.17: Densità a posteriori di Kn
Dall’ inferenza sul numero dei cluster si deduce che i pazienti possono appartenere a due gruppi (con una probabilità ∈ (0.2,0.3)), a tre gruppi (con una
probabilità ∈ (0.4,0.5)) oppure a 4 gruppi (con una probabilità pari a 0.2).
In quest’ultimo caso JAGS tende a sovrastimare il numero dei cluster.
3.3.4
Diagnostica di convergenza
Valgono le stesse considerazioni fatte per le simulazioni precedenti per quanto
riguarda la convergenza della catena: la catena è giunta a convergenza infatti
i traceplot sono molto fitti e l’ autocorrelazione è bassa.
66
3.4
CAPITOLO 3. SIMULAZIONI
Confronto dei risultati
Quindi osserviamo che i risultati ottenuti per i vari dataset simulati non sono
influenzati dalla funzione f che viene scelta nel modello.
Inoltre notiamo che le stime trovate per le diverse simulazioni confermano le
nostre aspettative: in tutti e tre i casi sia le distribuzioni marginali di G0 per
un nuovo paziente sia il numero di cluster sono come ci aspettavamo.
Capitolo 4
Analisi su dataset dei packages di
R
Vediamo ora come il modello descritto nel Capitolo2 possa essere impiegato
per analizzare un dataset ben noto in letteratura, presente in un package di R
(frailtypack). Tale dataset contiene i tempi di riospedalizzazione dei pazienti
a cui è stato diagnosticato un cancro al colon. I dati, presi dal dataset
readmmision, descrivono il tempo (in giorni) dei successivi ricoveri dopo la
data di intervento chirurgico; un totale di 861 eventi sono stati registrati per
i 403 pazienti inclusi nell’analisi.
I dati che abbiamo a disposizione sono (vedi Figura 4.1):
• id: identificatore dei pazienti
• time start: tempo in cui il soggetto è entrato nell’analisi o momento in
cui si è verificato l’evento precedente
• time stop: momento in cui si verifica l’evento di ospedalizzazione
• time: tempo tra due eventi, misurato in giorni
• chemo: variabile binaria che indica se il paziente ha ricevuto o meno la
chemioterapia
• sex: variabile binaria che indica il sesso del paziente (sex=1 se il paziente è uomo, sex=2 se il soggetto è donna);
67
68
CAPITOLO 4. ANALISI SU DATASET DEI PACKAGES DI R
• dukes: variabile categoriale che indica lo stadio del tumore (1= stage
A-B o 2=stage C o 3= stage D); al crescere del valore della variabile
dukes cresca la gravità del tumore;
• death: variabile binaria che indica la sopravvivenza del paziente (death=1
se il paziente è morto, death = 0 altrimenti)
• event: variabile binaria che indica la censura del dato (event = 0 se il
dato è censurato, event = 1 altrimenti)
• charlson: variabile categoriale che corrisponde all’indice della comorbidità di Charlson, può assumere i valori 0, 1-2, 3.
Figura 4.1: Estratto dal dataset "readmission"
4.1. IL MODELLO BAYESIANO
4.1
69
Il modello bayesiano
Seguendo la notazione del Capitolo 2, Wij rappresenta l’intertempo del jesimo evento per il paziente i. Consideriamo il seguente vettore di covariate
x := (x1 i, x2 i, x3 i, x4i (j)) con:
• x1i = chemo
• x2i = sex
• x3i = dukes
• x4i (j) = charlson
Quindi il modello diventa:
Yi1 =: logWi1 = x1i β1 + x2i β2 + x3i β3 + x4i (1)β41 + σεi1
Yij =: logWij = x1i β1 + x2i β2 + x3i β3 + x4i (j)β4j + αij + σεij
j = 1, · · · n
j = 2, · · · Ji
iid
con
εij ∼ N (0, 1)
e con Ji che indica il numero di eventi osservati per ogni paziente, in questo
caso J non è costante ma varia fra i vari individui. Qui n = 403. Si assume
che, condizionatamente ai parametri, i vettori Yi = (Yi1 , Yi2 , . . . , YiJi ) sono
indipendenti.
La tabella seguente contiene il numero di pazienti con j intertempi, con j
= 2,..,23.
Osserviamo che nell’ analisi non verranno considerati i pazienti con j = 1,
cioè i pazienti per i quali osservo un solo evento.
j
n.paz.
2
3 4 5 6 7 8 9 10 11 12,..,15
150 21 15 8 4 0 1 1 1 1
0
16 17,...,22 23
1
0
1
Tabella 4.1: Numero di pazienti con j intertempi, con j = 2,..,8
70
CAPITOLO 4. ANALISI SU DATASET DEI PACKAGES DI R
Per quanto riguarda la prior assumiamo che i blocchi (in θ) β, σ, (α1 , ..., αn )
siano indipendenti e che abbiano le seguenti distribuzioni:
σ ∼ U (0, 10)
 

0
 

 0 




β ∼ N   , 1000I 
,
 0 

0
dove β = (β1 , β2 , β3 , β4 ) e β4 = (β41 , β42 , . . . , β423 )
ind
αij | mi0 , mi1 , τ ∼ N (mi0 + mi1 logf (...), τ 2 )
iid
mi0 , mi1 | G ∼ G
G ∼ DP (M, G0 )
τ 2 ∼ inv-gamma(5, 1)
M =1
G0 = N (0, 10) × L(Z)
dove Z = 2X − 1, con X ∼ Beta(3, 3)
In questo capitolo confronteremo due possibili scelte per f :
• f (Wi1 , Wi2 , .., Wik ) = Wik
• f (Wi1 , Wi2 , .., Wik ) =
Wi1 +Wi2 +..+Wik
k
4.2. ANALISI DEI DATI
4.2
71
Analisi dei dati
Nella Figura 3.2 è rappresentato l’istogramma degli intertempi tra cui si
verificano due eventi per i diversi pazienti nel dataset considerato.
Figura 4.2: Istogramma degli intertempi in scala logaritmica
72
CAPITOLO 4. ANALISI SU DATASET DEI PACKAGES DI R
Analizzeremo le inferenze a posteriori per ogni possibile scelta di
f (Wi1 , Wi2 , .., Wik ):
• f (Wi1 , Wi2 , .., Wik ) = Wik
• f (Wi1 , Wi2 , .., Wik ) =
Wi1 +Wi2 +..+Wik
k
monitorando la distribuzione a posteriori di m0 new , la distribuzione a posteriori di m1 new e la distribuzione a posteriori di Kn , cioè il numero di valori
distinti di (mi0 , mi1 ) del campione dal processo di Dirichlet G.
Successivamente ci concentreremo sulle covariate: mostreremo gli intervalli di credibilità a posteriori per β1 , β2 , β3 , β4 e controlleremo la
convergenza.
4.3
Inferenza su
mnew
0 ,
mnew
1 ,
Kn
Come per il capitolo 3, la scelta della funzione f non influenza i risultati che
si ottengono per le stime a posteriori di m0 , m1 , Kn . Riportiamo quindi
per semplicità i grafici relativi ad un’unica scelta di f .
4.3. INFERENZA SU M0N EW ,
4.3.1
M1N EW ,
KN
73
Inferenza su m0
Figura 4.3: Densità a posteriori di m0 ,con f (Wi1 , Wi2 , .., Wik ) = Wik
La distribuzione del parametro m0 per un nuovo paziente è concentrata sul
valore 5.
74
CAPITOLO 4. ANALISI SU DATASET DEI PACKAGES DI R
4.3.2
Inferenza su m1
Figura 4.4: Densità a posteriori di m1 ,con f (Wi1 , Wi2 , .., Wik ) = Wik
La distribuzione del parametro m1 è costituita da due gobbe concentrate
attorno allo 0.
4.3. INFERENZA SU M0N EW ,
4.3.3
M1N EW ,
KN
75
Inferenza su K
Figura 4.5: Densità a posteriori di Kn ,con f (Wi1 , Wi2 , .., Wik ) = Wik
Dall’inferenza sul numero dei cluster si deduce che i pazienti possono appartenere a 3 , a 4 oppure (anche se con bassa probabilità) a 5 gruppi.
76
CAPITOLO 4. ANALISI SU DATASET DEI PACKAGES DI R
4.4
Inferenza sui parametri di regressione
Analizzeremo le inferenze per i parametri di regressione corrispondenti a
covariate che non variano fra gli intertempi, cioè:
• x1 = chemo
• x2 = sex
• x3 = dukes
4.4.1
Diagnostica di convergenza
Per prima cosa effettuiamo un’analisi di convergenza studiando l’ autocorrelazione, i trace plot e i valori della statistica di Geweke.
Esaminando tali output per (β1 , β2 , β3 ), sembra che la catena sia giunta
a convergenza. Infatti l’autocorrelazione (Figura 4.6) è sotto una soglia accettabile, i trace plot (Figura 4.7) sono molto fitti e gli z-scores (Figura 4.8)
si collocano nell’ intervallo [-2,2].
Figura 4.6: ACF plot di β1 = chemo, β2 = sex, β3 = dukes
4.4. INFERENZA SUI PARAMETRI DI REGRESSIONE
Figura 4.7: Trace plot di β1 = chemo, β2 = sex, β3 = dukes
Figura 4.8: Geweke plot di β1 = chemo, β2 = sex, β3 = dukes
77
78
CAPITOLO 4. ANALISI SU DATASET DEI PACKAGES DI R
4.4.2
Intervalli di credibilità a posteriori
Analizziamo ora gli intervalli di credibilità marginali a posteriori per β1 β2 β3 ,
in modo da comprendere in che modo le covariate influenzano la variabile
riposta.
Dagli intervalli di credibilità (Tabella4.1) e dalla densità a posteriori delle
covariate (Figura 4.10) emerge che:
• β1 , cioè la variabile binaria che indica se il paziente ha ricevuto o meno
la chemioterapia, non è significativa, perchè il valore 0 è un valore
centrale della marginale a posteriori di β1 ,
• gli individui di sesso maschile sono più soggetti a riospedalizzazioni,
• con l’aggravarsi dello stato del tumore si riducono gli intervalli temporali tra due ospedalizzazioni.
Figura 4.9: Densità a posteriori di β1 = chemo, β2 = sex, β3 = dukes
4.4. INFERENZA SUI PARAMETRI DI REGRESSIONE
beta1
beta2
beta3
79
Media
Varianza
2,5 %
50 %
97,5 %
-0.06468058 0.03944328 -0.4431969 -0.07158258 0.33840297
0.78545876 0.03564588 0.4202558 0.78314897 1.15384879
-0.34811612 0.01764422 -0.6078303 -0.34770471 -0.08244171
Tabella 4.2: Intervalli di credibilità marginali a posteriori per β1 , β2 , β3
4.4.3
Confronto dei risultati
Tali risultati possono essere confrontati con le stime ottenute attraverso lo
"Shared frailty model", contenuto nel pacchetto frailtypack di R da cui sono
stati presi i dati.
Questo modello è molto utile quando le osservazioni sono clusterizzate in
gruppi o quando le osservazioni sono degli eventi ricorrenti.
Nel seguito, useremo la terminologia per gli eventi ricorrenti introdotta nel
primo capitolo. Per il j − esimo (j = 1, ..., ni ) individuo del gruppo i −
esimo (i = 1, ..., N ), siano Wij gli eventi ricorrenti in fase di studio, Cij
i tempi censurati a destra e Lij i tempi di troncamento a sinistra. Definiamo le osservazioni Yij pari a min(Wij , Cij ) e gli indicatori di censura
δij = I{Yij =Wij } .
La funzione di rischio per il shared frailty model è
hij (w|vi ) = vi h0 (w)exp(βXij )
(4.1)
dove h0 (t) è la funzione di rischio base, Xij è il vettore delle covariate associato al vettore dei parametri di regressione β, e vi è l’ effetto casuale associato al
gruppo i-esimo. Assumiamo che vi siano i.i.d. da una gamma: vi ∼ Γ( 1θ , 1θ ).
80
CAPITOLO 4. ANALISI SU DATASET DEI PACKAGES DI R
La log-verosimiglianza ha la seguente formulazione analitica:
l(h0 , β, θ) =
ni
N n h X
X
i=1
+
δij ln hij (Yij )
i
j=1
1 h
ln 1 + θ
θ
ni
X
j=1
Hij (Lij )
i
−
1
θ
+ mi
+ I{ mi 6= 0}
ni
h
i
X
ln 1 + θ
Hij (Yij )
j=1
mi
X
o
ln 1 + θ(mi − k)
j=1
(4.2)
dove H0 (t) è la funzione di rischio cumulata base e mi è il numero degli
eventi ricorrenti.
Stima dei parametri attraverso lo Shared frailty model
Notiamo che per alcuni soggetti si verificano diverse ricadute. Logicamente,
possiamo immaginare che una correlazione all’interno dei tempi di ricaduta
potrebbe esistere.
Le righe seguenti corrispondono al codice R:
4.4. INFERENZA SUI PARAMETRI DI REGRESSIONE
81
Con la funzione print possono essere rappresentate le stime dei parametri
dei modelli.
In questo output possiamo leggere:
• coef: coefficienti di regressione
• exp(coef): Hazard ratios.
• SE coef (H): Errore standard stimato invertendo la matrice Hessiana.
• SE coef (HIH): Errore standard stimato utilizzando il prodotto tra
matrici H −1 IH −1 dove H −1 è l’inverso della matrice Hessiana e I è la
matrice dell?informazione di Fisher.
• z: Statistica di Wald
• p: p value, che è la probabilità P (| z |> 1.96). Se p <0.05, la covariata
è significativamente diversa da 0.
82
CAPITOLO 4. ANALISI SU DATASET DEI PACKAGES DI R
La varianza del termine fragilità θ è significativamente diversa da 0, il
che significa che vi è eterogeneità tra i soggetti. Possiamo dedurre questo
utilizzando un test di Wald modificato. Inoltre abbiamo un valore di p <
0,05 per le covariate dukes = 3, Charlson = 3 e per il sesso. Questo suggerisce
l’esistenza di un rischio più elevato di essere riospedalizzati per gli uomini
con lo stato di Dukes pari a 3 e un indice di Charlson a 3.
Il p-value corrispondente a chemo è > 10 %, cioè la covariate chemo non è
significativa.
Osserviamo quindi che tali risultati coincicono con le stime che erano state
trovate attraverso il nostro modello.
Capitolo 5
Analisi sui dati reali
5.1
Costruzione del Dataset
Il dataset è costituito da 1391 pazienti a rischio di infezione urinarie. Ogni
soggetto effettua diversi controlli ospedalieri, ognuno dei quali è caratterizzato da una variabile W BC che indica se il paziente è infetto (W BC > 0) o
meno (W BC = 0).
Riprendendo quindi la notazione del Capitolo 2, definiamo, ∀i, con Ti0 il
tempo della prima visita per cui la variabile W BC è maggiore di zero.
Stabilire i tempi degli eventi successivi è più complesso. Vediamo innanzitutto come stabilire il tempo Ti1 . Consideriamo i controlli ospedalieri successivi
al tempo Ti0 e ci fermiamo quando troviamo una visita in cui W BC = 0.
Consideriamo ora i controlli ospedalieri successivi a tale visita e ci fermiamo
quando troviamo una visita in cui W BC > 0. Possiamo quindi definire Ti1
come il tempo di questo controllo.
Definiamo Ti2 in modo analogo: consideriamo i controlli ospedalieri successivi al tempo Ti1 e ci fermiamo quando troviamo una visita in cui W BC = 0.
Consideriamo ora i controlli ospedalieri successivi a tale visita e ci fermiamo
quando troviamo una visita in cui W BC > 0. Possiamo quindi definire Ti2
come il tempo di questo controllo.
Iteriamo tale ragionamento per tutti i tempi successivi.
83
84
CAPITOLO 5. ANALISI SUI DATI REALI
Questo procedimento è chiaro se consideriamo la Figura 5.1 e la Figura
5.2 in cui sono rappresentati i tempi delle visite ospedaliere per due pazienti
scelti in modo arbitrario. In rosso sono rappresentati i controlli ospedalieri
in cui i soggetti sono sani (W BC = 0), mentre in verde sono evidenziate le
visite mediche in cui il soggetto presenta un’infezione, al contrario della visita
medica precedente in cui risultava sano, ossia le visite mediche che indicano
una nuova infezione.
Figura 5.1: Rappresentazione degli eventi per un generico paziente i
5.1. COSTRUZIONE DEL DATASET
85
Figura 5.2: Rappresentazione degli eventi per un generico paziente i
Ora possiamo quindi definire gli intertempi Wij = Tij − Tij−1 .
Durante tutte le analisi abbiamo considerato soltanto i pazienti con almeno
due intertempi, il dataset si è quindi ridotto e risulta costituito da n= 305
pazienti. La tabella 5.1 contiene il numero di pazienti con j intertempi, con
j = 2,..,9.
j
2
3 4 5 6 7 8 9
numero pazienti 121 89 54 21 10 6 2 3
Tabella 5.1: Numero di pazienti con j intertempi, con j = 2,..,9
86
CAPITOLO 5. ANALISI SUI DATI REALI
Osserviamo inoltre che tra la Figura 5.1 e la Figura 5.2 si nota una differenza: il paziente rappresentato nel primo grafico risulta infetto nell’ultimo
controllo mentre il paziente rappresentato nel secondo grafico è sano.
Abbiamo quindi introdotto i dati censurati per tutti quei paziente che nell’ultimo controllo non avevano un’infezione, infatti sappiamo solo che il nuovo
intertempo è maggiore del tempo che intercorre tra l’ultima visita e l’ultima
infezione.
Il numero di pazienti il cui ultimo dato è censurato sono 85, invece per i
rimanenti 220 soggetti l’ultimo dato non risulta censurato.
5.2
Il modello bayesiano
Basandoci sul modello introdotto nel Capitolo 2, definiamo:
∀i = 1, · · · , n
Yi1 =: logWi1 = x1i (1)β11 + x2i (1)β21 + x3i (1)β31 + x4i (1)β41 + x5i (1)β51 + σεi1
Yij =: logWij = x1i (j)β1j +x2i (j)β2j +x3i (j)β3j +x4i (j)β4j +x5i (j)β5j +αij +σεij ,
j = 2, · · · Ji
con
ind
εij ∼ N (0, 1)
Si assume che, condizionatamente ai parametri, i vettori Yi = (Yi1 , Yi2 , . . . , YiJi )
sono indipendenti.
Considerando le varie covariate xki (j), k = 1, · · · , 5, i = 1, · · · , n, j =
1, · · · , 9, osserviamo che l’indice k indica le diverse covariate, l’indice i si
riferisce ai vari pazienti ed infine l’indice j è necessario per individuare l’intertempo in cui ci troviamo.
Le covariate x1i (j), x2i (j), x3i (j), x4i (j), x5i (j), come già evidenziato prima,
variano fra i vari intertempi.
x1i (j) indica l’età standardizzata del paziente i-esimo, nell’intertempo jesimo; mentre le altre covariate x2i (j), x3i (j), x4i (j), x5i (j), che assumo valori
5.2. IL MODELLO BAYESIANO
87
0 − 1, si riferiscono ai diversi sintomi che il paziente può o meno presentare.
Ossia:
• x2i (j) = urgency, indica se il paziente i-esimo, nell’intertempo j-esimo
ha attivi sintomi del tipo "urgenza",
• x3i (j) = pain, indica se il paziente i-esimo, nell’intertempo j-esimo ha
attivi sintomi del tipo "dolore",
• x4i (j) = stress incontinence, indica se il paziente i-esimo, nell’intertempo j-esimo ha attivi sintomi del tipo "incontinenza da stress",
• x5i (j) = voiding, indica se il paziente i-esimo, nell’intertempo j-esimo
ha attivi sintomi del tipo "svuotamento".
E’ necessario studiare la dipendenza fra le varie covariate, in modo tale da
vedere se è possibile escluderne qualcuna. Dovremmo fare una scelta delle
covariate mettendo una prior di tipo spike and slab per le varie covariate, ma
non lo facciamo, da un lato, per motivi di tempo; dall’altro perchè la catena
markoviana prodotta da JAGS sarebbe poco efficiente.
Dunque per tutte le covariate sono stati effettuati dei test χ2 di indipendenza
a coppie. In questo test l’ipotesi nulla indica che le covariate sono indipendenti, quindi se si ottiene un p-value minore del livello di significatività 0.05
vuol dire che le covariate sono tra loro dipendenti.
Dalla Tabella 5.2 ,in cui sono indicati i p-value che si ottengono facendo dei
test a coppie fra le varie covariate (x2i (j), x3i (j), x4i (j), x5i (j)) , emerge
che:
• x2i (j) e x3i (j) sono indipendenti,
• x3i (j) e x4i (j) sono indipendenti,
• x5i (j) dipende da tutte le altre covariate (x2i (j), x3i (j), x4i (j)).
88
CAPITOLO 5. ANALISI SUI DATI REALI
x2 = urgency
x3 = pain
x4 = stress
x5 = voiding
x2 = urgency
0.0846
1.264·10−5
0.01388
x3 = pain
0.0846
0.7725
3.291·10−5
x4 = stress
1.264·10−5
0.7725
2.731·10−5
x5 = voiding
0.01388
3.291·10−5
2.731·10−5
-
Tabella 5.2: P-value ottenuti dai test χ2 di indipendenza a coppie fra le varie
covariate
Quindi x5 può essere eliminata e il vettore di covariate si riduce:
• x1i (j) = age
• x2i (j) = urgency
• x3i (j) = pain
• x4i (j) = stress
Per quanto riguarda la prior assumiamo che i blocchi (in θ) β, σ, (α1 , ..., αn )
siano indipendenti e che abbiano le seguenti distribuzioni:
σ ∼ U (0, 10)
 

0

 

0
  , 1000I  ,
β ∼N

0
 

0
dove β = (β1 , β2 , β3 , β4 ) e βk = (βk1 , βk2 , . . . , βk9 ), k = 1, . . . , 4
5.2. IL MODELLO BAYESIANO
89
ind
αij | mi0 , mi1 , τ ∼ N (mi0 + mi1 logf (...), τ 2 )
iid
mi0 , mi1 | G ∼ G
G ∼ DP (M, G0 )
τ 2 ∼ inv-gamma(5, 1)
M =1
G0 = N (0, 10) × L(Z)
dove Z = 2X − 1, con X ∼ Beta(3, 3)
Anche in questo capitolo confronteremo due possibili scelte per f :
• f (Wi1 , Wi2 , .., Wik ) = Wik
• f (Wi1 , Wi2 , .., Wik ) =
Wi1 +Wi2 +..+Wik
k
90
5.3
CAPITOLO 5. ANALISI SUI DATI REALI
Analisi dei dati
Nella Figura 5.3 è rappresentato l’istogramma degli intertempi tra cui si
verificano due eventi per i diversi pazienti nel dataset considerato.
Figura 5.3: Istogramma degli intertempi in scala logaritmica
5.3. ANALISI DEI DATI
91
Analizzeremo le inferenze a posteriori per ogni possibile scelta di f (Wi1 , Wi2 , .., Wik ):
• f (Wi1 , Wi2 , .., Wik ) = Wik
• f (Wi1 , Wi2 , .., Wik ) =
Wi1 +Wi2 +..+Wik
k
monitorando la distribuzione a posteriori di m0 new , la distribuzione a posteriori di m1 new e la distribuzione a posteriori di Kn , cioè il numero di valori
distinti di (mi0 , mi1 ) del campione dal processo di Dirichlet G.
Successivamente ci concentreremo sulle covariate: mostreremo gli intervalli di credibilità a posteriori per β1 , β2 , β3 , β4 e controlleremo la convergenza.
Passeremo poi ad analizzare la significatività di mi1 utilizzando il metodo
Stochastic search variable selection prior (SSVS ).
Per tutte le simulazioni di questo capitolo, tramite JAGS, sono state
eseguite 10.000 iterazioni di burn-inn, con thinning pari a 50, per un final
sample size di 5.000 iterazioni.
92
5.4
CAPITOLO 5. ANALISI SUI DATI REALI
Inferenza su
mnew
0 ,
mnew
1 ,
Kn
Come per i capitoli precedenti, la scelta della funzione f non influenza i
risultati che si ottengono per le stime a posteriori di m0 , m1 , Kn . Riportiamo
quindi per semplicità i grafici relativi ad un’unica scelta di f , per questo
capitolo è stata scelta f (Wi1 , Wi2 , .., Wik ) = Wi1 +Wi2k+..+Wik .
5.4.1
Inferenza su m0
Figura 5.4:
Densità a posteriori di m0 ,con f (Wi1 , Wi2 , .., Wik )
=
Wi1 +Wi2 +..+Wik
k
La distribuzione del parametro m0 , cioè la distribuzione della prima componente di G0 , per un nuovo paziente è concentrata sul valore 5.5 .
5.4. INFERENZA SU M0N EW ,
5.4.2
M1N EW ,
KN
93
Inferenza su m1
Figura 5.5:
Densità a posteriori di m1 ,con f (Wi1 , Wi2 , .., Wik )
=
Wi1 +Wi2 +..+Wik
k
La distribuzione del parametro m1 , cioè la distribuzione della seconda componente di G0 , è concentrata sul valore 0.1.
Questi risultati indicano che, sia il parametro m0 , che il parametro m1 influenzano la variabile risposta, poichè la densità a posteriori non include lo
0.
94
5.4.3
CAPITOLO 5. ANALISI SUI DATI REALI
Inferenza su K
Figura 5.6:
Densità a posteriori di Kn ,con f (Wi1 , Wi2 , .., Wik )
=
Wi1 +Wi2 +..+Wik
k
Dall’inferenza sul numero dei cluster si deduce che i pazienti possono appartenere a 2 gruppi oppure, con minore probabilità, ad un unico gruppo.
5.5. INFERENZA SU τ 2 E SU σ
5.5
95
Inferenza su τ 2 e su σ
In questa sezione analizziamo innanzitutto la posterior di σ, ossia la deviazione standard della variabile risposta. Ricordiamo infatti che:
Yi1 |β1 , σ ∼ N (xi β1 , σ 2 )
Yij |Yi1 , .., Yij−1 , βj , σ, αij ∼ N (xi βj + αij , σ 2 )
Figura 5.7: Densità a posteriori di σ
Dalla Figura 5.7 si nota che il supporto della posterior di σ è [0, 0.8] e
tale densità è concentrata prevalentemente nell’intervallo [0.5, 0.8].
96
CAPITOLO 5. ANALISI SUI DATI REALI
Vediamo ora la posterior di τ 2 , ossia la varianza dei parametri αij , infatti:
ind
αij | mi0 , mi1 , τ ∼ N (mi0 + mi1 logf (...), τ 2 )
con τ 2 ∼ inv-gamma(5, 1)
Figura 5.8: Densità a posteriori di τ 2
Dal grafico precedente, in cui sono riportate la prior (in blu) e la posterior
(in rosso) di τ 2 , si nota che il supporto delle due densità è equivalente e i due
grafici sono pressochè sovrapponibili.
5.6. INFERENZA SUI PARAMETRI DI REGRESSIONE
5.6
97
Inferenza sui parametri di regressione
Analizziamo ora le inferenze per i parametri di regressione corrispondenti alle
varie covariate:
• x1i (j) = age
• x2i (j) = urgency
• x3i (j) = pain
• x4i (j) = stress
5.6.1
Diagnostica di convergenza
In modo analogo al capitolo precedente, come prima cosa effettuiamo un’analisi di convergenza studiando l’autocorrelazione, i trace plot e i valori della
statistica di Geweke. Esaminando i vari output per β1 , β2 , β3 , β4 non si può
escludere che la catena sia giunta a convergenza. Infatti l’autocorrelazione è
bassa, i trace plot sono molto fitti e gli z-scores si collocano nell’ intervallo
[-2,2]. Vi sono dei grafici anomali per quanti riguarda l’ottavo e il nono intertempo poichè i dati a disposizione per questi due intertempi sono pochi
(infatti abbiamo 2 pazienti con j = 8 e 3 soggetti con j = 9). Per semplicità riportiamo i grafici relativi soltanto ad un parametro di regressione: per
l’autocorrelazione consideriamo β2 , utilizziamo i trace plot relativi a β1 ed
infine usiamo i Geweke plot del parametro β4 .
98
CAPITOLO 5. ANALISI SUI DATI REALI
Figura 5.9: ACF plot di β2
Figura 5.10: Trace plot di β1
5.6. INFERENZA SUI PARAMETRI DI REGRESSIONE
99
Figura 5.11: Geweke plot di β4
5.6.2
Intervalli di credibilità a posteriori
In questa sezione studiamo gli intervalli di credibilità marginali a posteriori
per β1 , β2 , β3 , β4 , per comprendere in che modo le covariate influenzano la
variabile riposta.
Riportiamo gli intervalli ottenuti relativi alle varie β:
• β1 , ossia il coefficiente che si riferisce all’età standardizzata dei pazienti.
beta11
beta12
beta13
beta14
beta15
beta16
beta17
beta18
beta19
Media Varianza
0.067
0.002
-0.077
0.002
0.052
0.004
0.052
0.010
0.278
0.024
-0.179
0.066
0.350
0.235
13.086 121.944
-22.476 923.972
2,5 %
50 % 97,5 %
-0.028
0.067
0.161
-0.173 -0.077
0.015
-0.075
0.052
0.181
-0.066
0.123
0.320
-0.021
0.277
0.582
-0.699 -0.181
0.313
-0.617
0.355
1.295
-1.586 10.642 38.079
-88.649 -19.102 28.652
Tabella 5.3: Intervalli di credibilità marginali a posteriori per β1
100
CAPITOLO 5. ANALISI SUI DATI REALI
Rappresentando graficamente gli intervalli di credibilità marginali a
posteriori per β1 si può vedere come varia l’influenza dell’età fra i vari
intertempi.
Non consideriamo per questa analisi j = 8 e j = 9 perchè, avendo
a disposizione pochi pazienti per questi intertempi, la varianza degli
intervalli di credibilità è elevata.
Figura 5.12: Intervalli di credibilità marginali a posteriori per β1
Innanzitutto si nota che al crescere del numero dell’intertempo aumenta l’ampiezza dell’intervallo di credibilità, questo poichè il numero dei
pazienti diminuisce e quindi c’è maggiore variabilità. Inoltre si osserva
che in tutti gli intervalli è contenuto lo zero, però esiste una differenza
fra i vari intertempi: alcuni intervalli contengono maggiormente valori
5.6. INFERENZA SUI PARAMETRI DI REGRESSIONE
101
positivi, mentre altri sopratutto valori negativi. Quindi se consideriamo
l’intertempo j = 2 e l’intertempo j = 6, i cui intervalli di credibilità
contengono soprattutto valori negativi, avremo che, considerando un
generico soggetto i, al crescere dell’età del paziente si riduce il tempo
di attesa tra un’infezione e la successiva. Al contrario, se consideriamo
l’intertempo j = 1, l’intertempo j = 3, l’intertempo j = 4, l’intertempo
j = 5 e l’intertempo j = 7, al crescere dell’età del paziente aumenta il
tempo di attesa tra un’infezione e la successiva.
Riportiamo anche la densità a posteriori per β1 , che conferma le analisi
precedenti:
Figura 5.13: Densità a posteriori di β1
102
CAPITOLO 5. ANALISI SUI DATI REALI
• β2 , ossia il coefficiente che si riferisce alla covariata che indica se il
sintomo urgenza è attivo nei diversi pazienti.
beta11
beta12
beta13
beta14
beta15
beta16
beta17
beta18
beta19
Media Varianza
0.245
0.011
0.077
0.008
-0.006
0.013
-0.006
0.027
0.437
0.134
0.559
0.286
-0.093
0.873
-9.508
58.097
-0.521 1006.553
2,5 %
0.037
-0.096
-0.227
-0.169
-0.305
-0.461
-1.912
-26.744
-62.835
50 % 97,5 %
0.245 0.449
0.076 0.254
-0.008 0.220
0.164 0.484
0.441 1.136
0.553 1.629
-0.105 1.730
-7.906 0.859
-0.392 61.631
Tabella 5.4: Intervalli di credibilità marginali a posteriori per β2
Rappresentando graficamente gli intervalli di credibilità marginali a
posteriori per β2 si può vedere come la seconda covariata influenza la
variabile risposta nei vari intertempi. Anche in questo caso non consideriamo l’intertempo j = 8 e j = 9 perchè, avendo a disposizione pochi
pazienti per questi intertempi, la varianza degli intervalli di credibilità
è elevata.
5.6. INFERENZA SUI PARAMETRI DI REGRESSIONE
103
Figura 5.14: Intervalli di credibilità marginali a posteriori per β2
Come per gli intervalli di credibilità marginali a posteriori per β1 si
nota che al crescere del numero dell’intertempo aumenta l’ampiezza
dell’intervallo di credibilità, questo poichè il numero dei pazienti diminuisce e quindi c’è maggiore variabilità. Inoltre si osserva che in tutti
gli intervalli è contenuto lo zero, eccetto per l’intertempo j = 1. In questo caso gli intervalli contengono maggiormente valori positivi, questo
vuol dire che per i pazienti che hanno attivo il sintomo del tipo urgenza
aumenta il tempo che intercorre fra le varie infezioni.
104
CAPITOLO 5. ANALISI SUI DATI REALI
• β3 , ossia il coefficiente che si riferisce alla covariata che indica se il
sintomo dolore è attivo nei diversi pazienti.
beta11
beta12
beta13
beta14
beta15
beta16
beta17
beta18
beta19
Media Varianza
0.021
0.009
-0.258
0.008
-0.195
0.014
-0.195
0.023
-0.581
0.102
0.398
0.099
0.916
0.344
10.436
79.376
8.588
868.091
2,5 %
-0.164
-0.441
-0.424
-0.509
-1.201
-1.013
-0.170
-1.586
-44.789
50 % 97,5 %
0.019 0.208
-0.260 -0.077
-0.196 0.042
-0.205 0.084
-0.582 0.053
-0.398 0.200
0.888 2.140
8.489 30.495
6.830 74.579
Tabella 5.5: Intervalli di credibilità marginali a posteriori per β3
Rappresentando graficamente gli intervalli di credibilità marginali a
posteriori per β3 si può vedere come la terza covariata influenza la variabile risposta nei vari intertempi.
Per le stesse motivazione relative ai coefficienti precedenti non consideriamo l’intertempo j = 8 e j = 9.
5.6. INFERENZA SUI PARAMETRI DI REGRESSIONE
105
Figura 5.15: Intervalli di credibilità marginali a posteriori per β3
Come per gli intervalli di credibilità marginali a posteriori per β1 e per
β3 , si nota che al crescere del numero dell’intertempo aumenta l’ampiezza dell’intervallo di credibilità, questo poichè il numero dei pazienti
diminuisce e quindi c’è maggiore variabilità. Inoltre si osserva che in
tutti gli intervalli è contenuto lo zero, eccetto per l’intertempo j = 2.
Al contrario del caso precedente, qui gli intervalli contengono maggiormente valori negativi (escluso l’intertempo j = 7) questo vuol dire che
i pazienti che hanno attivo il sintomo del tipo dolore hanno infezioni
più frequenti.
106
CAPITOLO 5. ANALISI SUI DATI REALI
• β4 , ossia il coefficiente che si riferisce alla covariata che indica se il
sintomo incontinenza da stress è attivo nei diversi pazienti.
beta11
beta12
beta13
beta14
beta15
beta16
beta17
beta18
beta19
Media Varianza
-0.095
0.015
-0.159
0.013
0.120
0.027
0.120
0.052
-0.162
0.234
-0.786
0.331
-0.812
0.457
15.675 153.607
10.282 732.527
2,5 %
50 % 97,5 %
-0.331 -0.094 0.143
-0.386 -0.158 0.061
-0.202 0.121
0.438
-0.465 -0.015 0.440
-1.140 -0.162 0.770
-1.894 -0.787 0.342
-2.141 -0.813 0.536
-0.554 12.864 43.859
-44.551 10.494 63.298
Tabella 5.6: Intervalli di credibilità marginali a posteriori per β4
Rappresentando graficamente gli intervalli di credibilità marginali a
posteriori per β4 si può vedere come l’ultima covariata influenza la
variabile risposta nei vari intertempi.
Anche in quest’ultimo caso non consideriamo l’intertempo j = 8 e j = 9
per analoghe motivazioni relative ai casi precedenti.
5.6. INFERENZA SUI PARAMETRI DI REGRESSIONE
107
Figura 5.16: Intervalli di credibilità marginali a posteriori per β4
Come per tutti i grafici precedenti , si nota che al crescere del numero
dell’intertempo aumenta l’ampiezza dell’intervallo di credibilità, questo
poichè il numero dei pazienti diminuisce e quindi c’è maggiore variabilità. Inoltre si osserva che in tutti gli intervalli è contenuto lo zero; per
l’intertempo j = 1, l’intertempo j = 2, l’intertempo j = 6 e l’intertempo j = 7 gli intervalli di credibilità sono concentrati su valori negativi,
mentre per l’intertempo j = 3, l’intertempo j = 4 e l’intertempo j = 5
gli intervalli di credibilità sono piuttosto simmetrici rispetto lo zero.
Quindi per pazienti che hanno attivo il sintomo del tipo incontinenza
da stress l’intertempo tra un’infezione e la seguente si riduce se j = 1,
j = 2, j = 6 oppure j = 7.
108
5.7
CAPITOLO 5. ANALISI SUI DATI REALI
Stochastic search variable selection per mi1
Dopo aver analizzato l’influenza che le covariate hanno sulla variabile risposta, in questo paragrafo ci concentriamo sull’importanza della seconda
componente di G0 .
Per svolgere tale analisi è stato utilizzato il metodo Stochastic search variable
selection (SSVS).
In tale modello la prior delle covariate è una mistura di densità "spike" e
"slab". La componente spike si concentra attorno allo zero e riflette l’assenza delle variabili nel modello, mentre la componente slab ha varianza
sufficientemente grande per permettere ai coefficienti diversi da zero di assumere valori maggiori.
Come componente spike è stata utilizzata una delta di Dirac concentrata
sullo 0, mentre come componente "slab" è stata utilizzata una Beta traslata
con supporto sull’intervallo [−1, 1].
La formulazione matematica è la seguente:
G0 = N (0, 10) × L(Z)
Z|γ ∼ (1 − γ)δ(0) + γS
S = 2X − 1, con X ∼ Beta(3, 3)
γ|w ∼ Bernulli(w)
w ∼ U nif orme[0, 1]
(5.1)
5.7. STOCHASTIC SEARCH VARIABLE SELECTION PER MI1
109
Con le scelte fatte precedentemente si ottiene la seguente densità a priori:
Figura 5.17: Densità a priori di m1
Per selezionare le variabili è stata utilizzata la tecnica Median probability model
(MPM). Tramite questa tecnica si selezionano le variabili per cui la probabilità a posteriori di inclusione nel modello è maggiore di 0.5. Poichè il livello
di troncamento della rappresentazione di Sethuraman nell’analisi è pari a 50,
avremo 50 valori per la probabilità a posteriori di inclusione di m1 nel modello.
Osservando il grafico seguente si nota che, in generale, la probabilità a posteriori di inclusione è circa 0.5, quindi mi1 è significativa per prevedere la
variabile risposta.
110
CAPITOLO 5. ANALISI SUI DATI REALI
Figura 5.18: Probabilità a posteriori di inclusione di m1
Bibliografia
Cook, R. J. e Lawless, J. F. (2007). The statistical analysis of recurrent events.
Springer, New York.
De Iorio, M., Johnson, W. O., Müller, P. e Rosner, G. L. (2009). Bayesian nonparametric nonproportional hazards survival modeling. In: Biometrics,
65, 762–771.
Ferguson, T. S. (1973). A Bayesian analysis of some nonparametric problems.
In: The Annals of Statistics, 1, 209–230.
Jackman, S. (2009). Bayesian analysis for the social sciences. John Wiley &
Sons.
Müller, P. e Mitra, R. (2013). Bayesian nonparametric inference. In: Bayesian
analysis, 8,
Müller, P., Quintana, F. A., Jara, A. e Hanson, T. (2015). Bayesian Nonparametric Data Analysis. Springer, New York.
Plummer, M. et al. (2003). JAGS: A program for analysis of Bayesian graphical models using Gibbs sampling. Proceedings of the 3rd international workshop on distributed statistical computing. Vol. 124. Technische
Universit at Wien.
Prentice, R. L., Williams, B. J. e Peterson, A. V. (1981). On the regression
analysis of multivariate failure time data. In: Biometrika, 68, 373–379.
Wang, M.-C., Qin, J. e Chiang, C.-T. (2001). Analyzing recurrent event data with informative censoring. In: Journal of the American Statistical
Association, 96, 1057–1065.
111
112
Bibliografia
Ringraziamenti
Desidero ricordare tutti coloro che mi hanno aiutata nella stesura della tesi
con suggerimenti, critiche ed osservazioni: a loro va la mia gratitudine.
Ringrazio anzitutto la Professoressa Guglielmi, Relatore di questo lavoro,
sempre disponibile a dirimere i miei dubbi durante la stesura. La sua guida e
i suoi consigli mi hanno permesso di completare al meglio questo elaborato.
Un ringraziamento particolare va alla Professoressa Maria De Iorio dell’University College London per i preziosi suggerimenti e le comunicazioni personali a cui non era obbligata.
Infine ringrazio tutte le persone a me care: la mia famiglia e i miei amici.
Un pensiero speciale va ai miei nonni e allo zio, che con il suo sorriso buono
e rassicurante mi faceva intuire la sua gioia e il suo orgoglio per il percorso
che avevo intrapreso e che stavo per concludere.
Marta
113