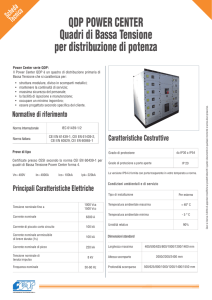
Un recipiente avente il volume di 6 litri è diviso in due parti A e B separate da una parete mobile e
conduttrice. Le pareti sono adiabatiche.
Lo scomparto A contiene una mole di gas monoatomico a
temperatura TA = 200K, mentre nello scomparto B c’è una mole di gas,
anch’esso monoatomico, a temperatura TB = 400K.
La pressione è la stessa nei due scomparti
VERSO QUALE STATO DI EQUILIBRIO EVOLVE IL SISTEMA?
Considerare separatamente due casi.
Caso A: la parete divisoria si muove liberamente senza attrito.
Caso B: la parete divisoria è fissa
Determinare:
a) la temperatura To di equilibrio
b) la variazione di Energia interna del sistema (∆U)
c) la variazione di Entropia del sistema (∆S)
FORMULE
Energia interna di una mole
di gas perfetto U=
Calore specifico molare di
un gas perfetto
monoatomico
CV =
volume costante
CP =
LEGGI
Equazione di stato dei gas
perfetti:
PV =n RT
Primo Principio della
Termodinamica
∆Q-∆L =∆U
pressione costante
STATO INIZIALE
Dall’equazione di stato
si ricava il rapporto tra i due volumi VA e VB
VA =⅟2 VB
Sapendo che VA + VB =6 l= 6 *10 -3 m3
VA = 2*10 -3 m3
VB=4*10 -3 m3
COSTANTI
R= 8,31 J K−1 mol−1
Anche se non richiesto, si può calcolare il valore della pressione
PA =PB=(R*10 5 = 8,31 10 5)Pa
Pressione
Scomparto A
8,31 10 5 Pa
Scomparto B
8,31 10 5 Pa
Volume
2* 10 -3 m3
4*10 -3 m3
Temperatura
200 K
400K
SOLUZIONE CASO A
Analisi qualitativa
Lo stato finale di equilibrio prevede che nei due scomparti si abbia la stessa temperatura e la stessa
pressione.
Poiché il numero di moli è lo stesso, i due gas occuperanno lo stesso volume, pari a metà del volume
complessivo
Il gas B, più caldo, cede calore al gas A più freddo che, riscaldandosi si espande .
A compie lavoro positivo e B fa lavoro negativo.
Il Sistema non scambia energia con l’esterno, né tramite lavoro, né tramite calore, quindi l’Energia interna
non varia ( ∆U=0)
Poiché la trasformazione è irreversibile l’entropia del sistema aumenta (∆S>0)
Analisi quantitativa
a)
STATO FINALE
V’A=V’B = 3l
Per determinare la temperatura di equilibrio impostiamo l’equazione
CP(TB-To)=CP(To-TA)
Ovvero
Dalle leggi di gas perfetti si ricava
la temperatura di equilibrio coincide con la media aritmetica delle due
temperature iniziali.
Ciò è conseguenza del fatto che le capacità termiche dei due corpi sono uguali
Pressione
Scomparto A
8,31 10 5 Pa
Scomparto B
8,31 10 5 Pa
Volume
3*10 -3 m3
3*10 -3 m3
Temperatura
300 K
300K
b)
∆U=0
- Verifica diretta
∆Q
∆L
∆U
A
CP∆TA
P∆VA
CV∆TA
B
CP∆TB
P∆VB
CV∆TB
∆Q
A
8,31*
∆L
8,31 *10 5 *10 -3 J
-8,31 *10 -3 J
0
∆U
8,31*
-8,31*3/2 J
0
VERIFICA DEL
PRIMO PRINCIPIO:
∆Q=∆L+∆U
8,31*
-8,31*
0=0
J
8,31
(1+3/2)
c)
=
>0
=
<0
B
- 8,31*
-8,31
J
(1+3/2)
Totale
0
L’entropia del gas A aumenta, mentre quella del gas B diminuisce
L’Entropia del sistema aumenta
∆S =
>0
SOLUZIONE CASO B
Analisi qualitativa
Lo stato finale di equilibrio prevede che nei due scomparti si abbia la stessa temperatura.
Poiché ciascun gas non varia di volume, le rispettive pressioni varieranno in modo direttamente
proporzionale alla temperatura
Il Sistema non scambia energia con l’esterno, né tramite lavoro, né tramite calore, quindi l’Energia interna
non varia ( ∆U=0)
Poiché la trasformazione è irreversibile l’entropia del sistema aumenta (∆S>0)
Analisi quantitativa
a)
STATO FINALE
Anche in questo caso la temperatura di equilibrio coincide con la media aritmetica delle due temperature
iniziali , 300K
Pressione
Scomparto A
12,46* 10 5 Pa
Scomparto B
6,23* 10 5 Pa
Volume
2*10 -3 m3
4*10 -3 m3
Temperatura
300 K
300K
b)
∆U=0
- Verifica diretta
∆Q
∆L
∆U
A
Cv∆TA
0
CV∆TA
B
Cv∆TB
0
CV∆TB
∆Q
A
8,31*
∆L
0
0
0
∆U
8,31*
-8,31*3/2 J
0
J
B
- 8,31*
J
Il Primo Principio è palesemente verificato
c)
=
>0
=
<0
L’Entropia del gas A aumenta, mentre quella del gas B diminuisce
L’Entropia del sistema aumenta
∆S =
>0
L’aumento di Entropia è però minore rispetto al caso A, essendo CV<CP
Totale
0