Perché la contrazione isotonica non esiste.
Quando diciamo contrazione isotonica, intendiamo una contrazione muscolare durante la quale il
tono del muscolo rimane costante per tutta la durata del movimento articolare (iso-tono = uguale
tono).
Bisogna però precisare, come già osservato da altri autori, che la contrazione isotonica è una
modalità di contrazione muscolare puramente teorica preferendo quindi il termine auxotonica (tono
variabile).
Come la biomeccanica insegna, la muscolatura prende inserzione sui segmenti scheletrici venendo a
realizzare quello che viene indicato come “angolo inserzionale”.
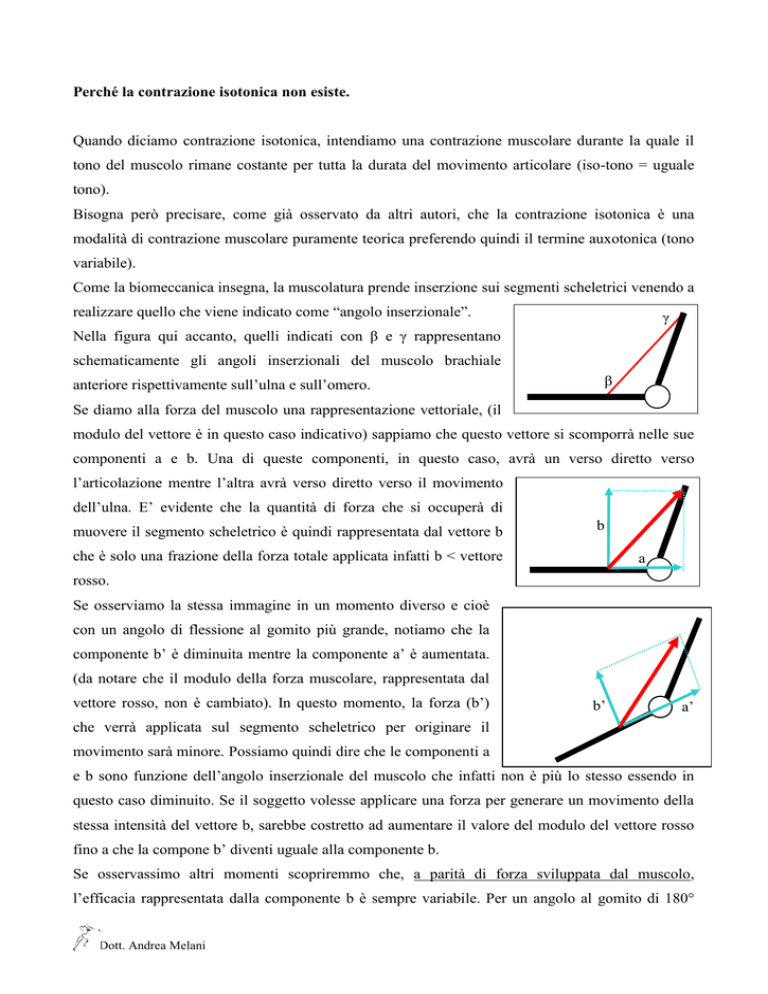
γ
Nella figura qui accanto, quelli indicati con β e γ rappresentano
schematicamente gli angoli inserzionali del muscolo brachiale
β
anteriore rispettivamente sull’ulna e sull’omero.
Se diamo alla forza del muscolo una rappresentazione vettoriale, (il
modulo del vettore è in questo caso indicativo) sappiamo che questo vettore si scomporrà nelle sue
componenti a e b. Una di queste componenti, in questo caso, avrà un verso diretto verso
l’articolazione mentre l’altra avrà verso diretto verso il movimento
dell’ulna. E’ evidente che la quantità di forza che si occuperà di
muovere il segmento scheletrico è quindi rappresentata dal vettore b
b
che è solo una frazione della forza totale applicata infatti b < vettore
a
rosso.
Se osserviamo la stessa immagine in un momento diverso e cioè
con un angolo di flessione al gomito più grande, notiamo che la
componente b’ è diminuita mentre la componente a’ è aumentata.
(da notare che il modulo della forza muscolare, rappresentata dal
vettore rosso, non è cambiato). In questo momento, la forza (b’)
b’
a’
che verrà applicata sul segmento scheletrico per originare il
movimento sarà minore. Possiamo quindi dire che le componenti a
e b sono funzione dell’angolo inserzionale del muscolo che infatti non è più lo stesso essendo in
questo caso diminuito. Se il soggetto volesse applicare una forza per generare un movimento della
stessa intensità del vettore b, sarebbe costretto ad aumentare il valore del modulo del vettore rosso
fino a che la compone b’ diventi uguale alla componente b.
Se osservassimo altri momenti scopriremmo che, a parità di forza sviluppata dal muscolo,
l’efficacia rappresentata dalla componente b è sempre variabile. Per un angolo al gomito di 180°
Dott. Andrea Melani
avremo una componente b dal valore quasi nullo per crescere fino ad un massimo verso i 100-110°
(quando il vettore rosso forma con l’ulna un angolo di 90°) per poi ricominciare a diminuire.
Se ipotizziamo ora di avere un carico di massa costante pari per esempio a 5Kg da dover muovere
attraverso la flessione del gomito, la componente b dovrà come minimo essere maggiore di 5Kg.
Per sviluppare una forza b pari a, per esempio, 5,5Kg, sarà necessario sviluppare una forza
muscolare tale da originare una componente b di 5,5Kg. Come dimostrato precedentemente, la forza
muscolare necessaria sarà variabile da un massimo (gomito a 180°) ad un minimo (gomito a 100110°).
Tutto questo facendo uno studio vettoriale della sola forza
muscolare. Se però facciamo uno studio vettoriale anche
della resistenza applicata (carico da muovere) scopriamo che
le variabili in gioco a questo punto diventano due poiché
anche il vettore b della resistenza avrà una modulazione della
sua intensità in funzione dell’atteggiamento del gomito.
a
Nell’esempio in figura, la resistenza genererà un momento
che sarà massimo quando l’ulna sarà orizzontale per
b
diminuire distendendo il gomito o flettendolo ulteriormente.
E’ necessario osservare che mentre lo studio vettoriale
dell’azione muscolare non cambia in funzione della stazione
del soggetto o dell’atteggiamento degli arti, lo studio vettoriale delle resistenze applicate varierà in
funzione della stazione, dell’atteggiamento degli arti e dell’attrezzo utilizzato come resistenza.
Basta pensare alla differenza tra l’utilizzo di un manubrio o di un bilanciere, che genereranno una
resistenza a direzione verticale verso il basso, e l’utilizzo di una ercolina che genererà una
resistenza la cui direzione sarà rappresentata dalla direzione del cavo.
Dott. Andrea Melani